Метод распознавания состояния групповой воздушной цели на основе модели со случайной скачкообразной структурой в интересах повышения эффективности бортовой радиолокационной станции истребителя

В варианте концепции всестороннего распознавания состояний воздушных целей (ВЦ) [1] отмечается, что для поддержки принятия решений летчиком и оптимизации наведения ракет существует острая необходимость в расширении информационных возможностей бортовой радиолокационной станции (БРЛС) истребителя.

Однако тактические характеристики БРЛС современных истребителей позволяют распознавать лишь тип летательного аппарата (ЛА) из класса «самолет с турбореактивным двигателем (ТРД)», численный состав группы до 10 целей, а также факты пуска ракет, что представляется недостаточным в сравнении с реальными вариантами воздушно целевой обстановки, включающими следующие состояния воздушных целей [1]:

Для одиночной ВЦ:

класс по принципу «ЛА с турбореактивным двигателем – ЛА с турбовинтовым двигателем – вертолет – ракета»;

тип воздушной цели;

характер полета по принципу «стационарный полет – маневр».

Для групповой ВЦ (ГВЦ):

численный состав группы;

типовой состав группы;

характер полета элементов ГВЦ по принципу «стационарный полет – маневр в группе – маневр составом группы»;

функциональное назначение самолетов в группе по принципу «ведущий – ведомый» в основных формах боевого порядка «пеленг», «клин», «фронт».

Для разделяющейся ВЦ:

факт разделения;

класс разделяющихся ВЦ по принципу «пилотируемый ЛА – авиационные средства поражения (АСП)»;

характер разделения группы по принципу «разделение по скорости – по направлению».

Для пилотируемых ЛА:

численный состав по принципу «сколько отделилось ЛА – сколько осталось ЛА в группе»;

характер полета каждой группы по принципу «стационарный полет – маневр в группе – маневр составом группы»;

при стационарном полете каждой группы: типовой состав; функциональное назначение («ведущий – ведомый» в формах боевого порядка «пеленг», «клин» «фронт».

Для АСП:

класс АСП по принципу «ракета – бомба»;

количество отделившихся АСП;

направление полета ракеты по принципу «на меня – не на меня»;

время, оставшееся до точки встречи ракеты с истребителем в случае ее наведения «на меня».

Важность и необходимость наличия этой информации на борту истребителя подтверждается результатами анкетирования летного состава [1].

Таким образом, тактические характеристики современных БРЛС не в полной мере соответствуют предъявляемым требованиям.

Результаты летно-экспериментальных исследований и анализ информационных свойств радиолокационных сигналов, отраженных от реальных ВЦ, позволили выявить устойчивые информационные признаки, подтверждающие принципиальную возможность распознавания требуемых состояний [2].

Специфической особенностью решения задачи распознавания в вышеупомянутом смысле выступает необходимость на основе одних и тех же результатов наблюдений совместно вынести два решения – указать одно из возможных состояний ГВЦ и оценить функциональносвязанные координаты (ФСК). При этом под ФСК понимаются дальности до элементов ГВЦ, радиальные скорости и ускорения взаимного сближения самолетов группы и истребителя-носителя БРЛС. Отмеченная особенность предопределила применение в «многогипотезном» подходе положений теории совместного оценивания и различения сигналов [3], позволившее учесть зависимость как размерности вектора фазовых координат, подлежащего оцениванию, так и его состава от состояний ГВЦ.

Основным недостатком алгоритмов [4], синтезированных при байесовском критерии оптимальности, является отсутствие подхода к нахождению совместной апостериорной плотности – 652 – вероятности векторов ФСК и состояния ГВЦ, на которой основывается получение оценок этих векторов.

Основным недостатком алгоритмов [5], построенных на многогипотезной калмановской фильтрации, служит то, что оценки, получаемые на их основе, не оптимальны в смысле [3].

Также следствием применения в «многогипотизном» подходе теорий линейной калманов-ской фильтрации и теории совместного оценивания и различения сигналов признаны следующие ограничения и допущения:

не учитываются априорные сведения о динамике распознаваемых состояний ГВЦ;

не учитывается дополнительная статистическая взаимосвязь между ФСК и состоянием ГВЦ;

линейность моделей полета ГВЦ и БРЛС как системы наблюдения, положенных в основу синтезированных алгоритмов;

при решении задачи фильтрации не рассмотрены такие реальные динамические свойства измерителей, как инерционность, форсирование и запаздывание;

не рассматривается возможность комплексирования информации от измерителей ФСК и индикаторов состояния ГВЦ, в том числе отличных по физическим принципам от радиолокационных.

Таким образом, перспективные методы и алгоритмы [2, 4–6] распознавания не в полной мере способны реализовать потенциальные возможности БРЛС по достоверности и количеству получаемой в результате распознавания информации.

Возможным путем устранения отмеченных ограничений является моделирование полета ГВЦ и смены ее состояний как системы со случайной скачкообразной структурой (ССС), применение рекуррентных алгоритмов [7].

Цель статьи – разработать метод распознавания состояния групповой воздушной цели, реализуемый в алгоритме на основе модели со случайной скачкообразной структурой в интересах расширения информационных возможностей и повышения точностных характеристик бортовой радиолокационной станции истребителя.

Для этого необходимо решить следующие частные задачи: синтезировать при байесовском критерии оптимальности общий алгоритм совместного траекторного сопровождения функционально связанных координат и распознавания состояния системы «ГВЦ – БРЛС – индикатор – истребитель» со ССС;

синтезировать оптимальный алгоритм совместного траекторного сопровождения и распознавания состояния ГВЦ, представленной системой со ССС.

Как правило, метод распознавания включает алфавит классов, словарь признаков и решающее правило. При этом новым является метод, отличающийся от известных хотя бы одним элементом из этой совокупности.

В дальнейшем предполагается, что алфавит классов и словарь признаков заимствованы из метода распознавания, основанного на многогипотезном калмановском подходе [2, 4–6], а новизну разрабатываемого метода составляет новое решающее правило (алгоритм), основанный на модели со ССС.

Также предполагается, что время полета ГВЦ в одном состоянии значительно превосходит время ее переходного процесса в другое состояние.

Синтез при байесовском критерии оптимальности алгоритма совместного траекторного сопровождения функционально связанных координат и распознавания состояния системы «ГВЦ – БРЛС – индикатор – истребитель» со случайной скачкообразной структурой

Рассмотрим обобщенную систему «ГВЦ – БРЛС – индикатор – истребитель» [8] со ССС со следующей математической моделью:

для динамики ФСК xk+1 = фк (sk+1, xk, sk, 5k ),(1)

для их измерений в БРЛС и вспомогательных измерителях

Zk+1 = Vk (Xk+1, Sk+1, rk+1, Xk, Sk, Zk, rk, z),(2)

дд qk(sk+11 xk, sk), для индикатора состояния обобщенной системы nk+1(rk+1 | xk+1, sk+1, xk, sk, zk, rk),(4)

для неуправляемых случайных возмущений и помех ф k Sk --k), при начальных условиях f x•’1

Оптимальная оценка составного вектора ( x k , s k ) функционально-связанных координат x k и состояния ГВЦ s k на основе наблюдений БРЛС, вспомогательных измерителей z о^ = z 0 , z i , K , z k и индикатора r -^= r_n.r, k, r .на интервале [0, k ], при байесовском критерии оптимальности 0, k 0 , 1 , , k                            , ,

⁽ x k , s k ) б = arg inf R ⁽ x k , s k ; z o, k , r o, k ) ,                                        ⁽⁷⁾

xk,sk заключается в определении такой его оценки, для которой минимален апостериорный риск R(xk , sk ; z 0,k, r 0,k) (среднее значение выбранной функции потерь по апостериорной плотности вероятности) [3], определяемый как

R ( x_k , s_k; Z КГ, Г kt) = У fn ( x k , s k ; x k , s k ) f (x k , s k | z kt, r kt) dx k ,       (8)

0,k 0,k                                                0,k 0,k sk xk где П(Xk,Sk;x^, s^) — функция потерь, характеризующая потери при использовании оценок (xk,sk), в то время, когда истинные значения векторов ФСК и состояний ГВЦ равны (Xk, Sk);

f ( X k , S k | z 0,k , r 0,k ) - апостериорная плотность вероятности составного вектора состояния, включающего вектор ФСК и вектор состояния ГВЦ, при фиксированном наблюдении ( z r ) , которая определяется на основании формулы Байеса

0, k , 0, k ,

f (Xk+1, Sk+1 |z 0,k+1, r 0) = f (Xk+1, Sk+1\Zk+1, rk+1; z 0k, r 0k ) =

_ f ( Z k + 1 , r k + 1 \ X k + 1 , S k + 1 , z 0k , r 0k ) f ( X k + 1 , S k + 1 \ z 0k , r 0k )             ⁽⁹⁾

f ( z k + 1 , r k ^{+ 1}| ^z 0, ^k , r 0, ^k )

где f (Zk+1, rk+i | Xk+1, Sk+1, z 0"k, r 0"k) - условное распределение вероятности вектора наблюдения (zk+1, rk+i) при каждом фиксированном значении оцениваемого составного вектора (xk+1, sk+1) и истории наблюдения (z   , r   ); f (z^+1,rk+11 z q^, r q^) - априорное распределение сиг налов в БРЛС и индикаторе; f (xk+1, sk+1 | z ттт, r тут) - прогнозируемое (априорное) распреде-0,k 0,k ление вероятности составного вектора состояния (x , s ) при фиксированном наблюдении Д                        Р            v k1, ku Р Т Р

^{( z} 0,^{k , r} 0,^k ) ■

На основании (1)-(5) и марковского свойства случайного процесса [ x k , s k , z k , r k ] получаем

f(xk            ., r 0H)- f(xk.            rk+1; zk, rk)-

f ⁽ z k + 1 . ^r k + 1 1 x k + 1 . s k + 1 . z k . ^r k ) f ⁽ x k + 1 . s k + 1 1 z k . ^r k ) — .

f ^{( z} k + 1 . ^r k + 1 I ^z k . ^r k )

Для определения функции потерь в формуле (8) введем в рассмотрение нормированные потери [4], равные нулю, при одновременном выполнении следующих условий: вектор ФСК оценен правильно;

состояние ГВЦ определено правильно.

Если любая из компонент вектора ФСК или вектора состояния ГВЦ оценена неверно, то потери должны быть равны единице. При этом правильная оценка вектора ФСК x_k будет иметь место только в том случае, когда модуль разности истинного значения вектора x k и его оценки X k не будет превосходить некоторой величины е, которая определяется ошибками сопровождения фазовых координат.

Исходя из этого нормированная функция потерь для вектора состояний ГВЦ, состоящего из N компонент, и вектора ФСК, состоящего из M компонент, примет вид

NM

П ( x _k ,S k ; X k , S k ) = 1 - П K s (i) s (i) П 1 - X ( F j i = 1      ^{k k} j = 1

-

Fl- = )]=

= 1 -ft^kj»,(,) П +(^-IFj - Fl), kk i-1            j-1

„    Г1, при i = j,                               Г1, при x > 0,   , где Kij =)           - символ Кронекера; Z(x)= ^        n - функция Хэвисайда.

1 0,при i+j ,                      J^0, при^x . ⁰        -

В результате нормированный апостериорный риск примет следующий вид:

A

R ⁽ x k , s k ; z 0, k , ^r 0, k ) - Z J ¹ - П ^K s <- ) s k- ) s k x k - i 1

M

П xtf - |f, j 1

-

Fj|) f (xk,sk Iz 0,k,r 0,k)dxk .

R ⁽ x k , s k ^{; z} 0, k , r 0, k ) ^-Z J f ^{( x} k , s k ^{1 z} 0, k , r 0, k ) ^dx k s_k x_k

N

K ( i ) ( i ) s_k ( i ) s_k ( i )

s k i 1

M f П * - j F,|)/(Xk, Sk l xk L j=1                   _

z 0, k , r 0, k ) ^dx ^k .

С учетом того, что первое слагаемое равно единице,

N

^(k , ^k ; 0, ^k ,   0, ^k)      ?«  s ki ) s ki )

M

J П X^е — F j — F j ) / ( X k , S k I

X k L j = 1                   J

z _{0, k} , r _{0, k} ) dx_k .

Интеграл в правой части отличен от нуля только при F — F <  £, j = 1, M , а множитель jj

N

П K s (i) _s (i) отличен от нуля только при условии S k = S k . При выполнении этих условий выраже- i = 1 s k s k

ние преобразуется к виду

x ^k + "

R ( x k , s k ; z ok , r ok ) = ^{1 -}       I f ( x k , s k I z ok , r ok )dx k = ^{1 -} I f ( x k , s k I z ok , r ok ) dx k ■

,     ,         U^k — xk l <*}       ,     ,           4 s                 ’

Подставляя формулу (10) в выражение (12), получаем

-1/

R (^x    s ; z____ r ____) — 1 f (z    r | z r )

Xk + 1 + ₆                                                                                  (13)

^x    J f ( ^z k + 1 , r k + 1 I ^x k + 1 , s k + 1 , ^z k , r k ) f ( ^x k + 1 , s k + 1 I ^z k , r k ) ^dx k + 1 ^.

xk + 1 — ^£

Из анализа выражений (12), (13) следует, что минимизация апостериорного риска достигается путем максимизации величины интеграла в правой части полученного выражения. В результате совместная оптимальная по критерию минимума апостериорного риска оценка ( x_k , s_k )_б будет определяться как

( X к + 1 , 5 к + 1 ) б

xk + 1 + F

= argm ^axsuP 1 j ^{f (} x k + 1 , S k + 1 | x ^{k + 1} . ^{X k} + ¹ s

z 0, k + 1 , r 0, k + 1 ) dx k + 1 '

= arg max

^Sk + 1

Xt+,+ £ k suP1 j f (zk+1, rk+1 xk+1 I xk+1 -E

I x k + 1 , ^S k + 1 , ^z k , ^r k ) ^{f (} x k + 1 , ^S k + 1 | ^z k , r k ) dx k + 1

При условии унимодальности апостериорной плотности вероятности [4] на этапе сопровождения ГВЦ в (14) можно опустить знак интеграла. С учетом этого имеем

(xк+1,5к+1)б = argmaxsup^y(xk+1, sk+11 z 0k+i, r OkT")}= sk+1 xk+1

= argmaxsup ^ y ⁽ z k + 1 , r k +11 ^x k + 1 , s k + 1 , ^z k , r k ) / ^{( x} k + 1 , s k +11 ^z k , r k ^{) }} , s^{k + 1} x k + 1

из чего можно сделать вывод, что при выбранной нормированной функции потерь совместная оценка по критерию минимума апостериорного риска совпадает с оценкой по критерию максимума апостериорной вероятности.

На основании теоремы умножения вероятностей

f ⁽ x k + 1 , s k + 1 I z 0, k + 1 , r 0, k + 1 ) = p ⁽ s k + 1 I z 0, k + 1 , r 0, k + 1 ) f ⁽ x k + 1 I s k + 1 , z 0, k + 1 , r 0, k + 1 ) =

= f(xk+1 I z 0,k+1, r 0,k+1)p(sk+1 I xk+1, z 0,k+1, r 0,k+1) , из чего следует, что получение оптимальной оценки составного вектора (Xk, Sk) ФСК хк и состояния ГВЦ sk на основе наблюдений (z 0,k, r 0,k) при байесовском критерии оптимальности может осуществляться в три этапа:

xк+1(sk+1) = arg sup f (xk+11 sk+1, Z ,, r 0^), xk+1

sk+1 = argmaxip(sk+11Z 0к+1, r 0)f(xk+11 sk+1,Z ,, r ,.,, sk+1

xk +1 = L p(sk+11Z ok+, r ok+1 x+1( sk+1), sk+1                   ’’ или

'k ⁺1( k ⁺^     g S k + 1 P^ k ^{+ 1} ' k ^{+ 1,} 0 k ⁺ 1 , 0 k ⁺1) ,

< xk+1 = argsuplf(xk+11z 0,k+i, r 0,k+i) p (sk+11 xk+1,z 0,k+i, r 0,k+i) }, да

|Sk+.-!f (Xk+.|z m ,r № )sk+.(Xk+^k+1

На первом этапе находят условные оценки вектора ФСК (состояния ГВЦ) при фиксированном состоянии ГВЦ (фиксированных ФСК).

На втором этапе определяется безусловная оценка состояния ГВЦ (ФСК) с учетом полученных условных оценок вектора ФСК (состояния ГВЦ).

На третьем этапе вычисляют безусловные оценки вектора ФСК (состояния ГВЦ).

Таким образом, синтезирован при байесовском критерии оптимальности общий алгоритм (15), (16) совместного траекторного сопровождения функционально связанных координат и распознавания состояния системы «ГВЦ – БРЛС – индикатор – истребитель» со случайной скачкообразной структурой, отличающийся от известного [4, 9, 10] введением дополнительного третьего этапа нахождения безусловных оценок, обобщением на случай произвольного количества состояний, подлежащих распознаванию, и комплексированием информации, поступающей от БРЛС, вспомогательных измерителей и индикаторов, что способно повысить точность получаемых оценок. В ходе разработки алгоритма была получена нормированная функция потерь (11) общего вида для произвольного количества компонент векторов ФСК и состояния ГВЦ.

Для конкретизации алгоритма необходимо найти явные выражения для плотности распределения составного вектора ФСК и состояния ГВЦ.

Синтез оптимального алгоритма совместного траекторного сопровождения и распознавания состояния групповой воздушной цели, представленной системой со случайной скачкообразной структурой

Требуется найти апостериорное распределение (апостериорную плотность вероятности) f ( X k ,s ^r  ) = f _; ( x ^J составного вектора состояния' ( X „ „), включающего вектор

ФСК x k и вектор состояния ГВЦ s k , в момент времени k , основанное на наблюдениях БРЛС, вспомогательных измерителей z ,. ,= z n, z> к-, zt и индикатора r 777= r , r , k , r на интервале 0, k 0, 1, , k                             0, k 0, 1, , k

[0, k ].

По теореме умножения вероятностей f ( x z | y )

^{f (} x,z I y ) = f ⁽ z I y ) f ⁽ x I z,y ) ^ f ⁽ x I z,y ) = ... , _ , f ⁽ x , zb ) = f ^{( x} I У ) f ^{( z} I ^x , У) , f ( z | y )

при этом формула Байеса примет вид f (x\z, У ) =

f (x , z | y ) = f (х1У ) f (z\x , У ) f ( z | y )             f ( z | y )

Тогда на основании формулы Байеса и марковского свойства векторов [ X k , S k ] и n k = [ X k , S k , Z k , r k ], вытекающего из (1)–(5),

f(xk+1, sk+1|Z    ., r .) = f(xk+1, sk+i\zk+1, rk+1; z 0k, r 0k) =

= f ( X k + 1 , S k + 1 | Z k + 1 , r k + 1 ; Z k , r k ) =

f ⁽ x k + 1 , s k + 1 , z k + 1 , r k + 1 ^{| z} 0 k , ^r 0 k ) f ⁽ z k + 1 , r k + 1 ^{| z} Ok , ^r 0kk )

f (zk+1, rk+1 |xk+1, sk+1, z 0,k, r 0,k)f(xk+1, sk+1 |z o,k,r 0,kk f (zk+1, rk+11 z 0,k,r 0,k)

^{f (} z k + 1 , ^r k + 1 \ ^x + + 1 , ^s k + 1 , ^z k , ^r k ) ^{f (} x k + 1 , ^s k + 1 \ ^zk , ^r k ) f ( Z k + 1 , r k + 1 \ Z k , r k )

Воспользовавшись формулой полной вероятности, имеем f (zk+1, rk+1 I xk+1, sk+1, zk, rk ) = ^ J f (zk+1, rk+1, xk , sk I xk+1, sk+1, zk, rk ) dxk , sk xk f (xk+1, sk+1 I zk, rk ) = S J f(xk+1, sk+1, xk, sk I zk, rk ) dxk , sk -7

7 7

^{f ( z} k + 1 , r k +11 ^z k , r k ) = SS J J f ⁽ z k + 1 , r k + 1 , ^x k + 1 , s k + 1 , ^x k , s k 1 ^z k , r k ) dx k dx k + 1^.

s k + 1 s k -7 -7

Из теоремы умножения вероятностей следует: для числителя

w

E J ^{f (} z k + 1 , r k +11 x k + 1 , s k + 1 , x k , s k , z k , r k ) f ⁽ x k + 1 , s k + 1 , x k , sk । z k , r k ) dx k = s k —»

'

^ -If (zk+1| rk+1, xk+1, sk+1,nk )nk+1( rk+1| xk+1, sk+1, nk)x x f(xk+11 sk+1, xk, sk) qk(sk+11 xk, sk) f(xk, sk 1 zk, rk) dxk, для знаменателя f (Zk+1,rk+11 Zk,rk) = ZX J J f (Zk+1 I rk+1,Xk+1,Sk+1,ПкП+1(rk+1 | Xk+1,Sk+1,nk) X sk+1 sk -<»-<»

X f ( X k + 1 | S k + 1 , X k , S k ) q k ( S k + 1 | X k , S k ) f ( X k , S k | z k , r k ) dX k dX k + 1 .

Плотности вероятностей ^f (x k _я | s k ₊ i , x k , s k ) и ^f (zk_я | r k _+b x k _+b s k ₊ i , П к ) описывают распределения дискретных белых шумов, функционально связанных с дискретными белыми шумами ξ k и ζ k соответственно.

Для определения ^{f (} X k + 1 1 s k + 1 , ^x k , s k ) и ^{f (} z k + 1 1 r k _+b x k _+b s k + 1 , П к ) найдем условные харак^тер^{истические} функции соответственно векторов x k +1 и z k +1 при фиксированных { s k ₊1 , x k , s k ^} и { r k ⁺¹ , x k ⁺¹ , s k ⁺¹ ,^{n k }:}

g k + 1( . ) = M M » ^r X k + 1k k + 1 , X k , S k 3=

= : ^ "';■ • ,' ■;“ ' }’

• - p. ^p‘⁽‘ + 1 , ^k ’ ^k , ^k<&)’

  
  

g к + 1 ( _И ) = M [ exp ( . V» ^r Z k . | r _t + 1 , X k + 1 , S k + 1 , n _t 3=

= M [ exp i , « ' y k ⁽ x ^k + , ’ ^{S k} + , ’ r k + , , ⁿ k ’ e k ^{)| X k + 1,} s k ^{+ 1,} r k + ^1, _n k ) ] =

J {• ' (                  z )}dФ « 1^ )

-»

где T – символ транспонирования; M – символ математического ожидания.

Воспользовавшись свойством совместной функции распределения и теоремой умножения , фk(kk) фk(SkZk)z„, фk(ik^k) = фk(fk,Zk)Ф-^k).

Плотности вероятностей f((x н1$1 ri,xk,^ и f (zk^^r vl, x +bsk+1,,t) сязаны, ссот- ветственно, с g^+i(^) и g‘+1(^) обратным преобразованием Фурье

f ( x k _xl s _k ! x k s k ) = (2 _П ) - n x J _{gk 1}( ^ )exp{ - i ® ^T _Xk J d ®

-co

f ( z   I r x s _П) = (2 _П ) - n z J _g' ( ® )e_XP { — i to T z } d ®

-o

В итоге оптимальный рекуррентный алгоритм совместного траекторного сопровождения и распознавания состояния групповой воздушной цели, представленной системой со случайной скачкообразной структурой, примет следующий вид [7]:

to

/ f к + 1 ⁽ z k + 1 , r k + 1 ) , s k + 1

= 1, n ⁽ s ) , (19)

fk + 1 ( x k + 1 , s k + 1 ) E J ^ ( ^ k + 1 , П к ) dx k

Sk - с нормировочным коэффициентом

7 7 *z fk+i(zk+1,rk+1)- LL J Je (nk+1,nk)dxkdxk+1,

s^k . s k - ⁷ - ⁷

где

• ^{8 n} k + 1 , П к ) = fk ⁽ z k +11 x k + 1 , s k + 1 , r k + 1 , П к⁾ⁿk ⁽ r k +11 x k + 1 , s kVb 4 k ) X

ˆ

X fk(xk+11 sk+1, xk, sk) qk(sk+11 xk, sk) fk(xk, sk), и начальными условиˆями f0C.„, s.)=f*x„.s)                                                     (22)

сучетом введенных

• —    ^{+    +}       +    +    +     0. ^k + 1 0. ^k + 1

f ⁺ 1^{( k +} 1 , k +D /k ^{+ 1}( ^{k +} 1 , ^{k +1}1 o. k , o. k)

Плотности вероятностей f k ( X k _{+ 1}| • ) и f k ( Z k _{+ 1}| • ) после подстановки (17) в (18) примут ^вид                             -.

fk ⁽ x k + 1 1 s k + 1 ,x k ,s k ) = ^{(2 n} ) n x J J ^ex P ^{i ®^T[ Tk⁽ ^ k , s k + 1 ,x k ,s k ) ^- x k + 1 ]} ^ ^ф k⁽ ^ k ) d®,

-— -— fk (Zk+Ikk+1, Sk+1, rk+1, nk) = m m

=(2n)-nx J Jexp{z®7'Wk(xk+1,sk+1,rk+1,nk,zk)-zk+1]}^фk(Zk I ^k)d®, где ф k (^k) -[ф k (^k,Zk=„

-1/^

Фk (Zk I ^k ) = Фk (^k, Ck )Фk (^k ), с оценками, рассчитываемыми на основе найденной апостериорной плотности вероятности, pt (st) -|Л(xk.sk^xk, оптимальная по критерию максимума апостериорной вероятности оценка состояния ГВЦ

Уk = argmax pk (sk), sk(28)

/к (xk ) = E fk (xk, sk ), sk математическое ожидание ФСК

• x. = J fxk Ж.                               (30)

  ^- "

ковариационная матрица ФСК

.

R k = j V x k TA ⁽ x k )dxk , x. = xk - xk .                               ⁽³¹⁾

-®

Структурная схема синтезированного оптимального алгоритма совместного траекторного сопровождения функционально-связанных координат и распознавания состояния ГВЦ представлена на рис. 1.

Полученный оптимальный алгоритм совместного сопровождения и распознавания ГВЦ, представленной системой со ССС, отличается от известных одновременным:

учетом априорных данных о динамике распознаваемых состояний ГВЦ в виде условных вероятностей переходов (3);

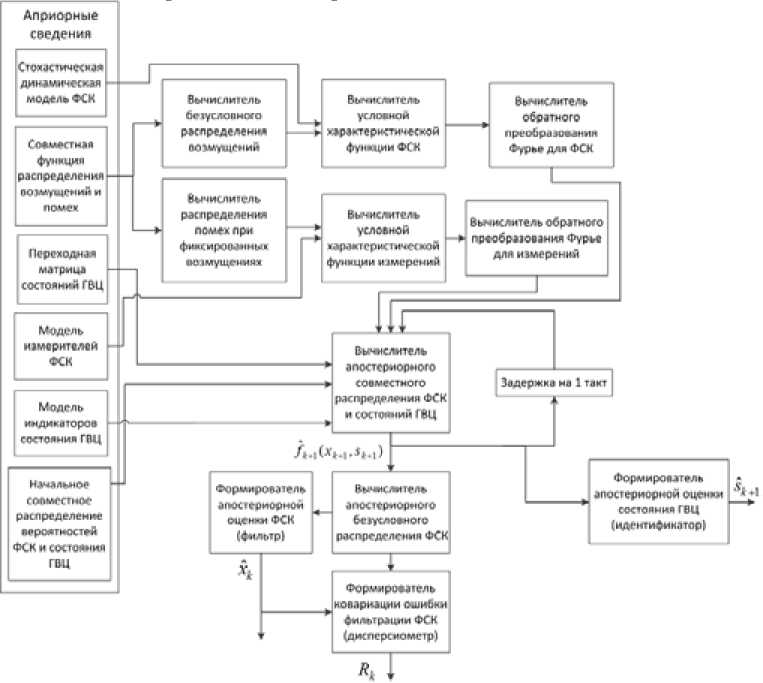
Рис. 1. Структурная схема оптимального алгоритма совместного траекторного сопровождения функционально-связанных координат и распознавания состояния ГВЦ

Fig. 1. Block diagram of an optimum algorithm of joint trajectory maintenance of the functional and connected coordinates and recognition of a condition of a group air target учетом дополнительной статистической взаимозависимости между ФСК и состоянием ГВЦ: в выражение (1) ФСК Xk+1 зависят от состояний ГВЦ Sk+1 и Sk, а в выражение (13) вероятности перехода qk(·) зависят от ФСК xk;

отсутствием ограничений на вид нелинейностей в моделях динамики ФСК (1) и их измерений (2);

учетом различных моделей движения ГВЦ посредством зависимости в выражение (1) ФСК X k +1 от состояний ГВЦ S k +1 и S k , причем модели могут отличаться как по структуре, так и по значениям используемых параметров;

учетом таких реальных нелинейных динамических свойств измерителей и индикаторов, как инерционность, форсирование и запаздывание (система наблюдения общего вида): в выражениях (2), (4) измерения z_{k +1} и показания индикатора r_{k +1} зависят от значений ФСК ( x_{k +1} ) и состояния ГВЦ ( s_{k +1} ) в текущий момент времени, от значений ( x_k ) и ( s_k ) в предыдущий момент времени и от измерений ( z_k ) и показаний индикатора ( r_k ) в предыдущий момент времени;

комплексным использованием информации от БРЛС, вспомогательных измерителей (2) и индикаторов (4), в том числе отличных по физическим принципам от радиолокационных;

совместным распознаванием состояния ГВЦ и оцениванием ее функционально связанных координат;

определением наиболее полной характеристики мгновенного состояния полета ГВЦ, а именно условной плотности вероятности f (Xk, Sk I z (к, r (k) составного вектора состояния (xk, sk), включающего вектор ФСК xk и вектор состояния ГВЦ Sk, в момент времени k, при фиксированных наблюдениях измерителя z (к = zq, Zi,k, zk и индикатора r ^^ = rQ, ri,K, rk на интервале [0, k];                                               ,                                                     , возможностью вычисления на основе найденной условной плотности вероятности любых вероятностных характеристик составного вектора состояния (xk, sk) и его компонент в отдельности, в том числе тех, которые могут быть приняты в качестве оптимальных оценок фильтрации sk и xk в зависимости от выбранного критерия оптимизации (например, для ФСК – математическое ожидание, медиана, мода);

гарантированной несмещенностью, эффективностью и состоятельностью оценок sk и хк, получаемых на основании плотности вероятности Л,(Хъ, st) при выполнении условия наблюдае-k k, k мости ГВЦ;

отсутствием необходимости для вычисления оценок s _k и x _k запоминать результаты наблюдений ^z 0М = z 0 ’ z l ’ к ’ z k - 1 ^{и r} 0Г1 = ^r 0 ’ r l ’ к ’ r k - 1 , ^{использ}уя ^{на k +1 шаге счета только два} последних измерения: z k , z k +1 и r k , r k +1 (следствие марковского свойства составного вектора [ ^x k , s k , z k , r k ^]);

изменением полосы пропускания фильтра в зависимости от текущих значений случайных возмущений, помех и сигналов управления;

статистической взаимозависимостью возмущений и помех;

в общем случае отличием числа измерителей, индикаторов и числа ФСК, состояний ГВЦ, подлежащих оцениванию (часть фазовых координат и состояний ГВЦ не наблюдаете неносред-ственно, а некоторые из фазовых координат и состояний ГВЦ измеряются двумя и более датчиками).

Это позволяет при осуществлении совместного сопровождения ФСК и распознавания состояния ГВЦ в БРЛС истребителя дополнительно учитывать:

закономерности смены различных состояний ГВЦ в случайные моменты времени;

зависимость численного состава ГВЦ, функционального назначения самолетов группы, формы ее БП, характера полета, вида помех, фактов пуска ракет, их количества и направления полета от радиальных дальностей, скоростей и ускорений;

ограничение допустимых диапазонов скоростей и ускорений летательных аппаратов, образующих ГВЦ, летно-техническими характеристиками их типов или классов;

ограничение возможных видов огневого и информационного противодействия, а также функционального назначения самолетов в группе их типами и классами.

Синтезированный оптимальный алгоритм фильтрации представляет собой функциональные интегральные рекуррентные уравнения для плотностей вероятностей составного вектора ФСК и состояния ГВЦ, поэтому его реализации в бортовой цифровой вычислительной машине (БЦВМ) истребителя, работающей в темпе динамики воздушного боя, существенно затруднена.

Практическая ценность синтезированного алгоритма состоит:

в осуществлении на основе его моделирования исследования потенциальных возможностей оптимального совместного оценивания и распознавания состояния ГВЦ в БРЛС истребителя;

в получении на основе синтезированной оптимальной структуры квазиоптимальных алгоритмов;

в проведении на основе моделирования сравнительного анализа характеристик полученных квазиоптимальных алгоритмов;

в обосновании требований к БЦВМ истребителя по объемам памяти и быстродействию для реализации перспективных оптимальных алгоритмов совместного оценивания-распознавания.

Заключение

Таким образом, разработан новый метод распознавания состояния групповой воздушной цели на основе модели со случайной скачкообразной структурой, отличающийся от известных новым решающим правилом.

Для этого синтезирован при байесовском критерии оптимальности общий алгоритм совместного траекторного сопровождения функционально связанных координат и распознавания состояния системы «ГВЦ – БРЛС – индикатор – истребитель» со ССС, дающий оптимальную структуру подсистемы распознавания и отличающийся от известного нормированной функцией потерь общего вида и дополнительным учетом показаний индикатора состояния ГВЦ.

Синтезирован оптимальный алгоритм совместного траекторного сопровождения и распознавания состояния ГВЦ, представленный системой со ССС и отличающийся от известных одновременным учетом априорных данных о динамике распознаваемых состояний и дополнительной статистической взаимозависимости между ФСК и состоянием ГВЦ, расширенными возможностями по комплексированию информации от вспомогательных измерителей и индикаторов, а также учетом ряда других существенных факторов.

В совокупности реализация полученных результатов на борту истребителя способна улучшить тактические характеристики бортовой радиолокационной станции по сопровождению и распознаванию групповых воздушных целей.

Работа выполнена при поддержке РФФИ (проект 16-08-00464а).