Метод разложения Тейлора для улучшения прогнозной силы регрессионных моделей

С целью уменьшения ошибки прогнозирования исследователь может разработать модель с учетом структурных сдвигов в исследуемых процессах и изменчивости коэффициентов в регрессионном уравнении2.

Представим, что разрабатывается модель для прогнозирования инфляции экономики США. Выберем в качестве выходной переменной коэффициент прироста квартального индекса потребительских цен (ИПЦ). В качестве возможных зависимых переменных будем тестировать по три лага зависимой переменной и y_t каждого коэффициента прироста квартального индекса для следующих макроэкономических индикаторов:

• •    ВВП;

• •    ВНД;

• •    ставка по централизованным кредитным средствам;

• •    численность занятых в несельскохозяйственном секторе;

• •    цена на нефть марки Brent;

• •    денежный агрегат М2;

• •    промышленный индекс Dow Jones;

• •    РВВП (реальный валовой внутренний продукт);

• •    полный экспорт;

• •    полный импорт;

• •    скорость денежного обращения;

• • безработица.

Уравнение регрессии может быть записано следующим образом:

3 n 3

y,+i=aо+е a^t-,+zz bx,              «>

j = 1                 i = 1 j = 1

где n– число объясняющих переменных, ajи bij– коэффициенты лагового ИПЦ и лаговых объясняющих переменных соответственно, a0 – константа модели

Мы не принимаем во внимание нулевые лаги, так как все макроэкономические данные недоступны в начале следующего за отчетным периодом, а публикуются позже в рамках квартала. Поэтому невозможно осуществить прогноз в начале квартала, если разработанная модель опирается на эти данные. Для построения модели используем 95 наблюдений, начиная с I квартала 1960 г. После того как первое уравнение рассчитано, окно данных передвигается вперед на одно наблюдение и уравнение пересчитывается. Данная процедура повторяется 70 раз. Для спецификации уравнения регрессии решалась оптимизационная задача.

MSE ® min

' a k <  0,05;

m ^J 10;

н VF J 7;

CN J 6;

1,5 <  DW <  2,5

где MSE – средняя ошибка прогноза, ak – уровень значимости для k-го предиктора, k ‚ [1..m], m – количество отобранных предикторов,

VIF_k – фактор расширения дисперсии для k -го предиктора,

CN – индекс обусловленности.

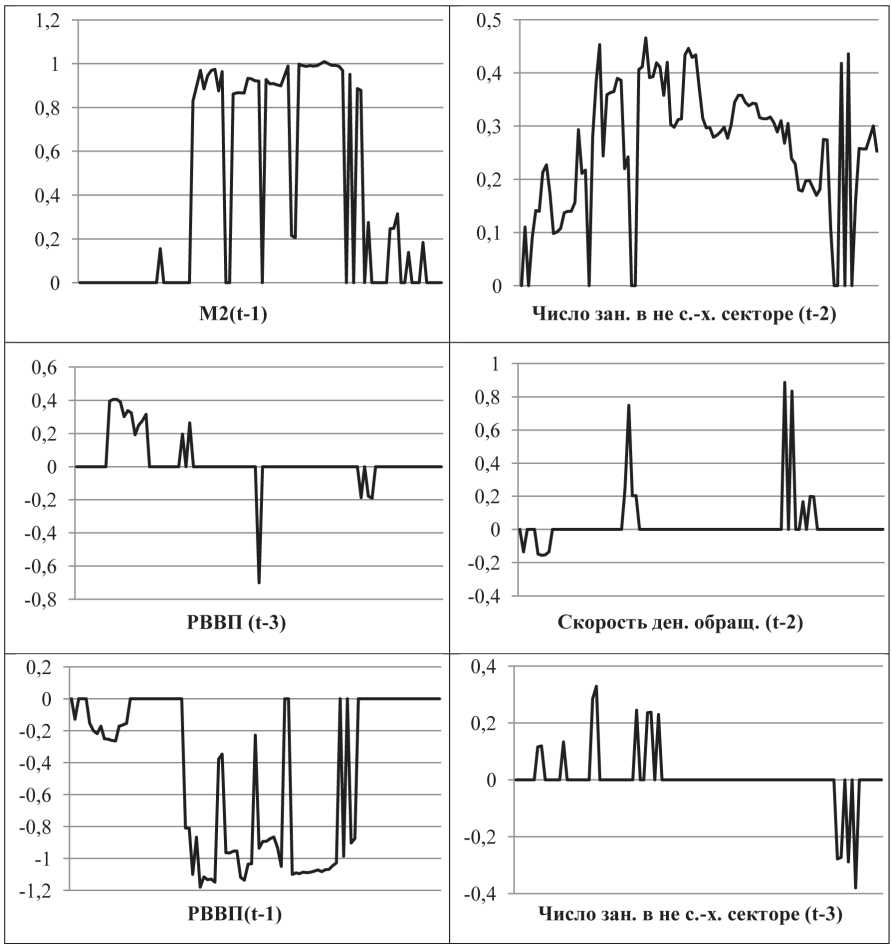
Не столь важен способ отбора переменных, главное, что мы выбираем наиболее качественное уравнение из возможных согласно заданному алгоритму. Для того чтобы проиллюстрировать неустойчивость структуры регрессионного уравнения, рассмотрим динамику коэффициентов на протяжении 70 полученных уравнений. Результаты приведены в табл. 1.

Из табл. 1 видно, что существуют более или менее устойчивые предикторы – М2 ( t -1), число занятых в несельскохозяйственном секторе ( t -2) и РВВП ( t -1), так и совершенно неустойчивые: РВВП ( t -3), скорость денежного обращения ( t -2) и численность занятых в несельскохозяйственном секторе ( t -3).

Выявилось огромное количество структурных сдвигов во время вычисления уравнений. Почти при каждом сдвиге окна данных могла быть построена другая регрессия, которая была лучше предыдущей. Более того, некоторые коэффициенты даже меняли свой знак. Это наводит на мысль о том, что коэффициент при предикторе на самом деле является не константой, а функцией, зависящей от других факторов. Также можно предположить, что при опущении предикторов, на самом деле влияющих на зависимую переменную, факторы, учтенные в уравнении, принимают на себя часть их влияния на выходную переменную модели.

К примеру, М2 ( t -1) часто ведет себя как весьма значительный предиктор (коэффициент относительно высок). Тот факт, что показатель М2 ( t -1) не учтен в уравнении с целью устранения мультиколлинеарности, не означает, что данный показатель утратил свое влияние на ИПЦ. Оно просто перераспределяется между коэффициентами предикторов, вошедших в модель. И если во время прогнозирования М2 ( t -1) начнет показывать более высокую волатильность, рассчитанная модель не будет устойчивой, так как не включает М2 ( t -1) в качестве объясняющей переменной.

Таблица 1. Динамика значений коэффициентов при предикторах

Методические выкладки

Пусть имеется целевая переменная и некоторый набор независимых переменных ( x 1 , x 2. „ x n ) . Необходимо построить линейную регрессионную модель

• У, = a 0 + a 1 x 1, + a 2 x 2, + - + a n x nt + e ⁽ t ) . (3)

Из табл. 1 видно, что коэффициенты при предикторах в некоторых случаях меняют знак в уравнении регрессии. Это значит, что степень влияния того или иного предиктора может зависеть от экономической ситуации в данный момент времени, то есть от величин других предикторов, участвующих в построении модели. Предположим, что коэффициенты при предикторах не являются константами, а некоторым образом зависят от величин, влияющих на модель факторов.

a i = f_x ( t> x 2 — x- 1 , x_{i +} 1 — X n ).                                            ⁽⁴⁾

Уравнение (3) можно записать в следующем виде:

У 1 = a 0 ^{+ f} . ⁽ x 2t , x 3 1 ^— x nt ) ^{X X} 1 1 ^{+ f} 2 ⁽ x 1t , ^X 3 1 ^— x nt ) ^{X X} 2 1 ^{+ —}

• ^{— + f} n ^{( X} 1t , ^X 2 1 ^{— X} ( n - 1) 1 ) ^{X X}„t ⁺ e ^{( 1} )                                ⁽⁵⁾

Поскольку мы не знаем вид ни одной из функций f (x1, x 2 — x-1, x/+1 — xn), будем использовать разложение Тейлора к -го порядка.

Для разложения в ряд Тейлора функции n переменных f (x1, x2 — xn), которая в некоторой окрестности точки (x10, x20 • — xn0) имеет полные производные до k-го порядка включительно, введем дифференциальный оператор

S             X                      S

T = (x1 - x10)— + (x2 - x20)— + — + (xn - xn0) — оx1             оx 2                  оxn

Тогда разложение функции в ряд Тейлора по степеням ( _x . - _x . 0 ) j в окрестности точки ( x ₁₀, x ₂₀ — x n ₀) имеет вид

f ^{( x} 1 , ^x 2 ^{— x} n ) = е T f ^{( x} 1⁰ , ^{x 20} —^x n0⁾ + R_k ^{( x} 1 , ^x 2 ^{— x} n ),              ⁽⁷⁾

j = 0             j !

где R_k ( x 1 , x ₂ — x n ) — остаточный член ряда.

Перепишем уравнение (5) с использованием (7), опуская k -й член ряда.

_    , У ^T 1 f l ( x 20, x 30 ’" x n 0)_YV

+

yt=a0+е                   ×x1t j=0                j !

+ e T 2 ^f >  ⁽ x 10 , x 30 ' "  "  x n 0 )

j = 0

j !

x x 2 t +—

^k T^jf ( x , x

x ( n - 1)0 )

× x_nt + e ( t )

+ n J n V 10, 20

е j=0                  j !

В качестве примера, полагая, что x_{i 0}= 0 , разложим регрессионное уравнение, представленное в (8), до второго порядка. Число независимых переменных примем равным 3. Тогда формула (6) может быть представлена в следующем виде:

T 1

¶¶ = x + x , ² ¶ x ₂ ³ ¶ x ₃

T

¶¶ = x + x , ¹ ¶ x ₁ ³ ¶ x ₃

T

¶¶

= x + x .

¶ x ₁       ¶ x ₂

Уравнение (8) примет следующий вид:

y t = a 0 +жзи ^{f 1 (} ₂ ⁰ _! ^,0) × T 1² + ^{f 1 (} ₁ ⁰ _! ^,0) × T 1 + f 1 (0,0) цчш× x 1 t +

+^жз_и ^{f 2 (} ₂ ⁰ _! ^,0) × T 2² + ^{f 2 (} ₁ ⁰ _! ^,0) × T 2 + f 2 (0,0) ^цч_ш× x 2 t +

+^жз ^{f 3 (} ₂ ⁰ _! ^,0) × T 3² + ^{f 3 (} ₁ ⁰ _! ^,0) × T 3 + f 3 (0,0) ^цч× x 3 t + e ( t )

иш   (10)

Подставляя значения T_i из (9) в (10), получим

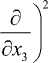
₊ f 1 (0,0) ж _x ¶

1! зи ^{2 t} ¶ x ₂

¶ ц 3 t ч⁺ ¶ x ₃ ш

f (0,0) ж ¶ y_t = a ₀ + ( ¹ з x _{2 t}     + x _{3 t}

2! и¶ x ₂

₊ f 2 (0,0) 1!

+ f (0,0)) × x + ( ^{f 2 (0,0)} ж x ^¶ + x ^¶ ц 11 t 1 t 3 t

2! и¶ x ₁ ¶ x ₃ ш

涶ц         f (0,0)涶ц зx1t+x3tч+f2(0,0))×x2t+( 3 зx1t+x2tч+ и¶x1¶x3ш                       2! и¶x1¶x2ш

+ ^{f 3 ( , )} x + x + f (0,0)) × x + e ( t )

1 1 t 2 t                   3                     3 t

! и¶ x ₁ ¶ x ₂ ш

Раскрыв скобки и приведя подобные члены в (11), получаем

y t = a 0 + f 1 (0,0) x 1 t + f 2 (0,0) x 2 t + f 3 (0,0) x 3 t +

ж¶ f (0,0) ¶ f (0,0) цж¶ f (0,0) ¶ f (0,0) ц

+з 1 + 2 ч xx +з 1 + 3       ч xx +

¶ x ¶ x              ¶ x ¶ x 21   31

ж¶ f (0,0) ¶ f (0,0) ц¶ 2 f (0,0)     2

+з 2 + 3         ч x 2 x 3 + 1 x 1 x 2 +

и¶ x 3 ¶ x 2 ш 2 ¶ x 2

¶ 2 f (0,0)     2    ¶ 2 f (0,0) 2 ¶ 2 f (0,0)     2              (12)

+ 1 xx + 2 xx + 2     xx + 2     x 1 t x 3 t             2     x 1 t x 2 t             2     x 2 t x 3 t

x 3                    x 1 x 3

¶ 2 f (0,0) 2 ¶ 2 f (0,0) 2

+ 3 xx + 3 xx +

2 ¶ x 1 21 t 3 t       2 ¶ x 2 22 t 3 t

ж¶ 2 f 1 (0,0) ¶ 2 f 2 (0,0)    ¶ 2 f 3 (0,0) ц

+++ xxx + e ( t )

и ¶ x 2 ¶ x 3       ¶ x 1 ¶ x 3       ¶ x 1 ¶ x 2 ш

Уравнение (12) может быть переписано следующим образом:

y t ⁼ a 0 ⁺ b 1 x 1 t ⁺ b 2 x 2 t ⁺ b 3 x 3 t ⁺ b 4 x 1 t x 2 t ⁺ b 5 x 1 t x 3 t ⁺

⁺ b 6 x 2 t x 3 t ⁺ b 7 x 1 t x 2 t ⁺ b 8 x 1 t x 3 t ⁺ b 9 x 1 t x 2 t ⁺ b 10 x 2 t x 3 t ⁺                    (13)

⁺ b 11 x 1 ² t x 3 t ⁺ b 12 x 2 ² t x 3 t ⁺ b 13 x 1 t x 2 t x 3 t ⁺ e ( t )

где проводятся следующие замены коэффициентов при регрессорах:

b1=f1(0,0),b2=f2(0,0),b3=f3(0,0),b4=жз¶f1(0,0)+¶f2(0,0)цч, и¶x2¶x1ш ж ¶f1(0, 0)   ¶f3(0,0)ц      ж¶f2(0,0) ¶f3(0,0)ц      ¶2f1(0,0)

b=з            +            ч,b=з             +            ч,b= и¶x3¶x1ши¶x3¶x2ш2¶x22

b ₈

¶ ² f 1 (0, 0) _{b =} ¶ ² f 2 (0,0) _{b =} ¶ ² f 2 (0,0) _{b =} ¶ ² f 3 (0,0) 2 ¶ x ₃ ^2,9 2 ¶ x ₁ ^2,10 2 ¶ x ₃ ^2,11       2 ¶ x ₁ ²

¶ ² f 3 (0, 0) _{b =}жз ¶ ² f 1 (0,0) ₊ ¶ ² f 2 (0,0) ₊ ¶ ² f 3 (0,0) цч

2 ¶ x ₂ ^{2     13} и¶ x ₂ ¶ x ₃ ¶ x ₁ ¶ x ₃ ¶ x ₁ ¶ x ₂ ш

Проводя оптимизацию полученного уравнения для имеющихся наблюдений, получим оценки коэффициентов (b1…b13), которые из (12) могут дать исследователю некоторое понятие о виде фукций 4. Разработанный прием помогает понять и описать структуру взаимосвязей экономических процессов. Более того, из 3 первоначальных независимых переменных мы получили 13, что существенно увеличивает потенциал регрессионного уравнения, вводя нелинейные кросс-связи между предикторами.

Пример расчета

Рассчитаем два регрессионных уравнения, удовлетворяющих системе ограничений (2), одно из которых строится по традиционной методике (R1), а второе – с учетом переменных, полученных с помощью метода разложения Тейлора до первого порядка (R2). Краткая сводка по полученным моделям представлена в табл. 2.

Таблица 2. Сводка по регрессионным уравнениям R₁ и R₂

Показатель	R1	R2
m	7	9
R	0.922	0.945
F -стат. знач.	0	0
DW	1.757	1.599
α	ИПЦ ( t -1) – 0 ВВП ( t -2) – 0 ЧЗНС ( t -2) – 0 Brent ( t -2) – 0.021 Dow Jones ( t -1) – 0.003 РВВП ( t -1) – 0.022 экспорт ( t -1) – 0.012	ИПЦ ( t -1) * безр-ца ( t -2) – 0 ИПЦ ( t -2) * ИПЦ ( t -3) – 0 ИПЦ ( t -3) * экспорт ( t -2) – 0 ИПЦ ( t -1) – 0 Dow Jones ( t -1) – 0.003 экспорт ( t -1) – 0 экспорт ( t -2) – 0 ск. ден. об. ( t -1) – 0.013 безр-ца ( t -3) – 0.023
VIF	ИПЦ ( t -1) – 3.179 ВВП ( t -2) – 4.373 ЧЗНС ( t -2) – 1.753 Brent ( t -2) – 1.142 Dow Jones ( t -1) – 1.179 РВВП ( t -1) – 1.817 экспорт ( t -1) – 1.723	ИПЦ ( t -1) * безр-ца ( t -2) – 1.481 ИПЦ ( t -2) * ИПЦ ( t -3) – 3.473 ИПЦ ( t -3) * экспорт ( t -2) – 4.219 ИПЦ ( t -1) – 4.091 Dow Jones ( t -1) – 1.113 экспорт ( t -1) – 3.131 экспорт ( t -2) – 4.684 ск. ден. об.( t -1) – 1.299 безр-ца ( t -3) – 1.939
CN	4.225	5.633
MSE	0.63767	0.54086

Для сравнения результатов на данных за пределами выборки было выбрано окно данных в 30 наблюдений, начиная с первой прогнозной величины, и рассчитан показатель MSE для всех 3 рассматриваемых уравнений. Данная процедура проводилась 25 раз при каждом из которых окно данных смещалось на единицу вперед.

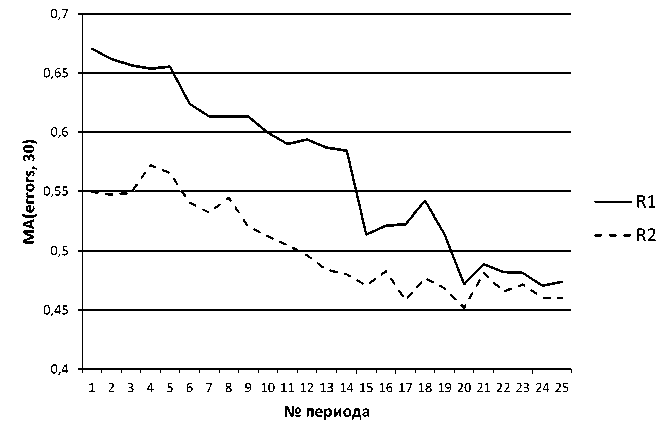
Из рисунка видно, что регрессии R ₂ соответствует более качественный прогноз, нежели R ₁ . Применение рассматриваемой методики к спецификации регрессионного уравнения с целью прогнозирования временных рядов является более целесообразным.