Метод решения дифференциальных уравнений с переменными коэффициентами в виде функции Хевисайда

Рассмотрим, линейное однородное уравнение n-го порядка в виде

у^(п) + Q1 (ж) у^(п-1) +-----+ а_п-х (ж) у⁽¹⁾ + а_п (ж) -у = 0,                    (1)

где коэффициенты а1 (ж), а₂ (ж), • • • , а_п (ж) содержат функции Хевисайда Н (ж — ж© г де ж^ - к точек, в которых функции Хевисайда неопределены, но ограничены.

Решение ДУ (1) ищем в виде

к

У = У 1 + ^2(Уі +1 - Уі)Н (ж - ж»).                           (²)

г=1

Подстановка (2) в (1) приведет к системе обыкновенных дифференциальных уравнений и условий в точках ж = ж^.

2.    Примеры решения дифференциальных уравнений, содержащих функции Хевисайда

Рассмотрим метод решения уравнений (1) на примерах.

Пример 1.

Найти фундаменталную систему решений для дифференциального уравнения

У(2)(ж) + Н(ж - Ж1)у(ж) = 0,                                 (3)

в котором Qi (ж) = 0,О2(ж) = Н (ж — жі) - это смещенная функция Хевисайда [1]. Решение уравнения будем искать в виде [2]:

у(ж) = У1 (ж) + (У2(ж) — У1(ж))Н (ж — ж1).                          (4)

Продифференцируем два раза у (ж) по переменной ж и получим

У(1)(ж) = У(1) + (У2(ж) — У1 (ж))

5(ж

Х = Х 1

^{— ж}1) ⁺ (у^{(1) (ж)}

— У(1)(ж)) Н(ж — жД,

У⁽²⁾(ж) = у ⁽²⁾ + ^21) (ж) — У⁽¹⁾(ж))

5(ж

Ж=Ж 1

^—ж0 + (у2 ^{2) (ж)}

— у(2)(ж)) Н(ж — жД.

Здесь Н‘ (ж — жД = 5 (ж — жД - 5-функция Дирака, применяя её свойства [2], получаем

(У2(ж) — У1(ж))

=0

(У(1)(ж) — У(1)(ж))

- условия совмещения в точке ж = ж1.

=0

Ж = Ж 1

После подстановки в (3) выражений (4) и (5), уравнение (3) распадется на систему из двух дифференциальных уравнений и условий (7):

У(2)(ж) = 0, У(2)(ж) — У(2)(ж) + У2(ж) = 0,

(У2(ж) — У1(ж))

= 0,

Ж=Ж 1

(У(1)(ж) — У(1)(ж))

= 0.

Решая (7) и подставляя в (4), получим ответ для (3) в виде функции, содержащей функции Хевисайда:

у(ж) = С1 COs(ж₁)(ж — жД + С₂ SІn(ж₁)(ж₁ — ж) + Cl SІn(Ж1) + С₂ cos(ж₁) +

< + [С1 (sin(ж) — COs(ж1 )(ж — жД — SІn(Ж1)) + C2(cos(ж) — SІn(ж1)(ж1 — ж) — cos(ж1))] Н(ж — жД, С1,С2 = const.

Таким образом, фундаментальная система функций имеет вид

У1(ж) = cos(ж1)(ж — жД + sin(ж1) + [sin(ж) — cos(ж1)(ж — ж1) — sin(ж1)]Н (ж — ж1);

У2Д) = Sin(x1)(x1 — x) + COs(X1) + [cos(x) — Sin(x1)(x1 — x) — cos(x1)]H (x — X1).

Пример 2.

Найти фундаменталную систему решений для дифференциального уравнения d4y   dd

dx4   dx^

Пользуясь свойствами d-функции, запишем

d(d) = d(yd)	— Д = y(X1)	dy -	d.	(9)
dx у    dx	dx       7 dx	dx	X=X 1

Подставим (9) в (8) и получим d4y        dd   dy dx4       7dx dx

d = 0.

X=X 1

Решение уравнения будем искать в виде (4). Найдем производую ^*4 для (4) и подставим в (10):

y⁽⁴⁾⁽x) + ⁽y2⁴⁾ (x) ^— y(" ⁽ x ^{))h (}x ^— X1) + (^(x) ^— y^x))

+(y22)(x) — y(2)(x))

dd, dx

X=X 1

— y(1)(x)

d = 0.

X 1 =X

d+

X=X 1

Группируя по функциям H0(x — Xi), H(x — Xi), d и d^, получим f      y(4)(x)=0,

( y24)(x) — y(4)(x) = 0.

Условия сопряжения:

d2(x)

y(1)(x)

= yi(x)

= y(1)(x)

,

,

y(3)(x)

y22)(x)

= y(3)(x)

+ У1 ( x )

+ y(1)(x)

= y(2)(x)

,

.

X=X 1

Решая систему (12) и пользуясь (13), в результате получим

y(x) = C₁(x³ + 2 (x — 2x₁)(x — x₁)²x1 H (x — x ₁ )) + +C₂(x₂ + 6 (2x — 5x1)(x — x₁)²x₁H (x — x ₁ )) + +Ca(x + 6 (x — 4x1)(x — x₁)²H (x — x ₁ )) + +^4(1 — 2 (x — X1)²H (x — X1)).

Таким образом, фундаментальная система функций имеет вид

' Г!(x) = x3 + 2(x — 2x1)(x — x1 )2x1H(x — x1), y2(x) = x2 + 6 (2x — 5x1)(x — x1)2x1H (x — X1), p3(x) = x + 6 (x — 4x1)(x — x1 )2H (x — x1),

_         У4 (x) = 1 — 2 (x — x1)2H (x — x1).

3.    Приложение метода решения ДУ к задаче механики

Рассмотрим композиции из трех элементов сферы-цилиндра-сферы, находящейся под действием внутреннего или внешнего давления [3].

Композицию из трех элементов сфера-цилиндр-сфера, отнесем к декартовым координатам ^j(j = 1,2,3) с началом в центре одной из сфер (рис. 1). Введем угол Ө между отрицателвным направлением оси £3 и вспомогателвним вектором f, определяющим положение любой точки меридионалвной кривой относителвно точки О' (рис. 1).

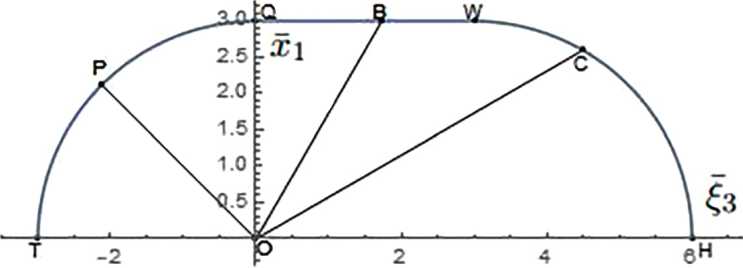
Рис. 1. Меридианальная кривая оболочки из трех элементов сферы-цилиндра-сферы

Обобщенный вектор положения г точки на меридионалвной кривой (рис. 1) имеет вид г (Ө) = r і + (гп - fi) Н (Ө - Өі) + (гш - гц) Н (Ө - Ө2),             (16)

r_i = R sin Өх 1 + R (-cos Ө) ^ ₃ ,r_ii = Rx 1 + R (- cot Ө) £ ₃ ,гш = R sin(- 2Ө)х 1 + R (1 + cos2Ө) £ 3, Ө і (i = 1, 2) - углы совмещения элементов композиции: Ө 1 = ^, Ө2 = 3^.

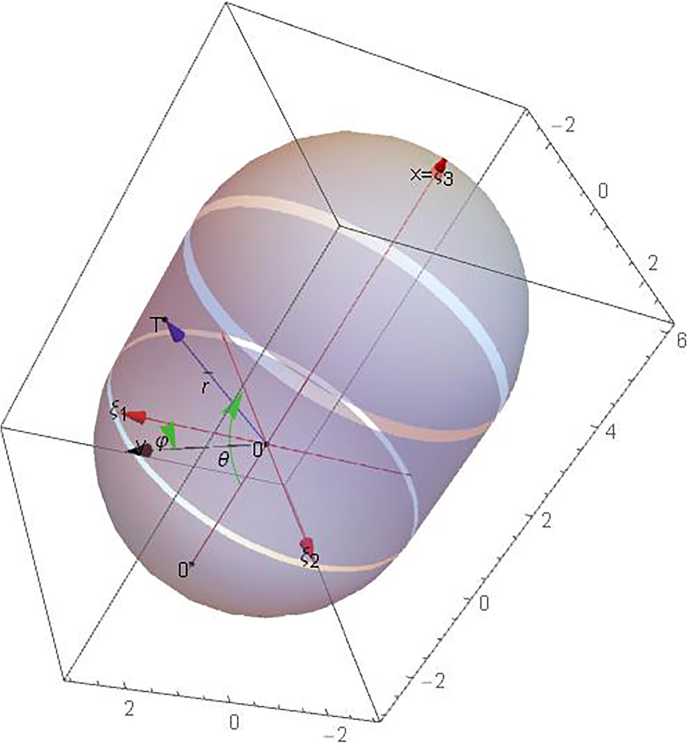
Рис. 2. Оболочка из сферы-цилиндра-сферы

Так как Х 1 = (cos(у) £1 + sin (у) £2), ^то выражение (16) для любой точки срединной поверхности композиции примет вид (рис. 2). Здесь у - угол поворота в плоскости О£₁£₂.

т(0, у) =

= (R [(— cos Ө) + [(— cot Ө) — (— cos 0)] Н(Ө — 01) + [(1 + cos 20) — (— cot Ө)\Н(Ө — Ө₂)\) £3+

+ (R [(sin Ө + (1 — sin Ө)] Н (Ө — 01) + (sin(—20) — 1)Н(Ө — Ө₂)) х (cos(у)£₁ + sin(у)£₂).

Композиция находится в безмоментном состоянии. В этом случае система уравнений безмоментной осесимметричной термоупругости для композиции сферы-цилиндра-сферы имеет вид

(V^G22^TП) ,1 + Д^СЙ^{Т 12,}2 ^— (Д^С22) ,1 ^{Т 22 +} V^Gn^G2291 = О,

< VG11T22,2 + (VG22T12) ,1 + (VG22) ,1 Т12 + VG11G2292 = 0,            (17)

Т 11^1 + Т ²²^2 = 93-

Здесь Сц = (ту)² - параметры Ламе, г = 1, 2, 1 - соответствует 0 и 2 - соответствует у. кг = пт^ - главные кривизны для данной оболочки, ттг = £,1- х —0= - вектор нормали ^ ii                                                                V^11    V^22

к касательной плоскости оболочки.

т,1 = Н (Ө — f) + (—2cos(20) — 0)Н (6 — 3^)] ( х х (cos(у)£1 + sin(у)£2) +

+^R [sin⁶ + (SisJrs — sin») ^Н (6 — 2) + (—2sm(2⁰) — s^;) ^H (6 — 32)] Ь.

T, 2 = (R [sin Ө + (1 — sin Ө) Н (Ө — 2) + (sin( —20) — 1)Н (Ө — 32)]) (— sin(у)£1 + cos(у)£2) .

Параметры Ламе для оболочки из трех элементов сфера-цилиндр-сфера:

^ = ^R [^{1 +} (^,

^— 0^н (^{ө —т})⁺(^2—

лУН(Ө — т)],

VG22 = R

sin Ө + (1 —

sin Ө)Н (ө — ^т) + (sin(—2Ө) — 1)Н (ө — 3^Т) .

Запишем вектор нормали п к касательной плоскости оболочки, и координаты данного вектора будут равны:

п =

^т,1 _х    ^т,2

VG11   VG22 ,

п = — (sin Ө + (1 — sin Ө) Н (Ө — ?) + (— sin(20) — 1) Н (Ө — 3 ? )^ х (cos(у)£₁ + sin(у)£₂)+ + ⁽cos Ө + (0 — cos Ө)Н (Ө — 2) +(— cos(26) — 0) Н (Ө — ³²£3,

Вычислим главные кривизны к1 и к2:

к1 = П • ^у1 и к2 = П • ^Д,

С11            С22

к1 = R (1 + (0 — D Н (ө — т) + (1 — 0) Н (ө — і^) у к2=R(1+(1—1)Н (Ө—т)+(1—1)н(ө—3т) )=R -

Парамеры Ламе VСц, VG22 и главные кривизны к1, к2 полученные для композиции сфера-цилиндр-сфера удовлетворяют условию Кодацци-Гаусса-Петерсона.

Получим аналитическое решение для усилий Т ¹¹ и Т ²² оболочки вращения, зависящих от Ө и <р. Построим и проанализируем их графики.

Так как оболочка вращения находится под постоянным давлением, то q 2 = q₁ = 0 и Т ¹² = 0. таким образом, в системе пропадет второе уравнение. Выразим Т ²² из 3-го уравнения системы (3):

Т ²² = Т (q3 -Т ¹¹ к 1 )

К 2

и подставим это в (3).

Решение ищем для Т ¹¹ в виде

Т ¹¹ = Т1 + (Т 2 - Т1) Н(Ө - Ө1) + (Тз - Т 2 )Н(Ө - Ө2).

Подставим выражение главных кривизн, параметра Ламе и (19) в (3), получим

(Тз),1

-

(Ті Ц + 2Т1 ctg Ө = Rq₃ ctg Ө,

(Т2),1

-

^(Т1 ),1 = ^Rq 3 ^{(- ctg(—2Ө))},

№),1 - 4Т3 ctg(-2Ө) + 4Т 2 ctg(-2Ө) = -2Rq3 ctg(-2Ө),

<

[Тз - Т2]

[Т2 - Т1]

= 0, 0 = 0 2

= 0 . 0 = 0 1

Решая (20), получим

Т ¹¹ = Д2 3 и Т ²² = Д2 3 (1 + (2 - 1) Н (Ө - Ө₁) + (1 - 2) Н (Ө - Ө₂)).

На рис. 3 и 4 приведены усилия Т ¹¹ и Т ²² для композиции сферы-цилиндра-сферы гладко сопряженных между собой, находящейся под постоянным давлением. Как видно из рисунков, усилие Т ²² в месте сопряжения элементов терпит разрыв 1-го рода - скачок на величину ^23. При решении задачи с введением дополнительной нагрузки на цилиндре в виде q = Р(Н (Ө - Ө₁) - Н (Ө - Ө2)), в которой коэффициент Р подбирается таким образом, чтобы уменьшить величину скачка, добиться положительного результата не удалось.

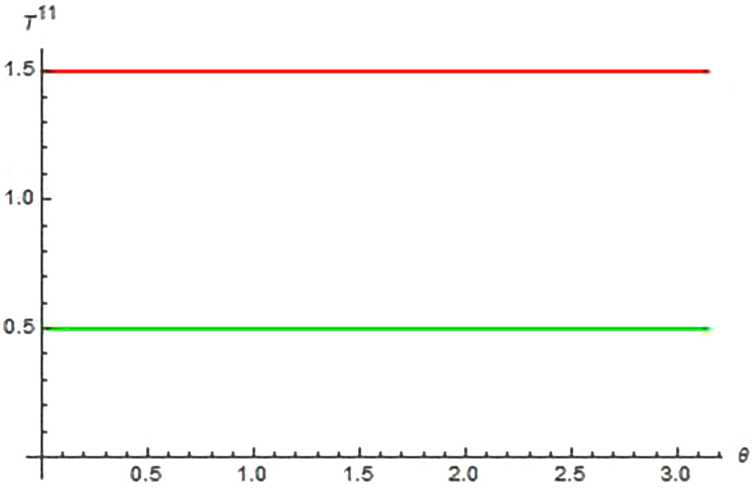
Рис. 3. Усилие Т 11, при R = 3, qa = 1 - верхняя линия, R = 2, q3 = 0.5 - нижняя линия

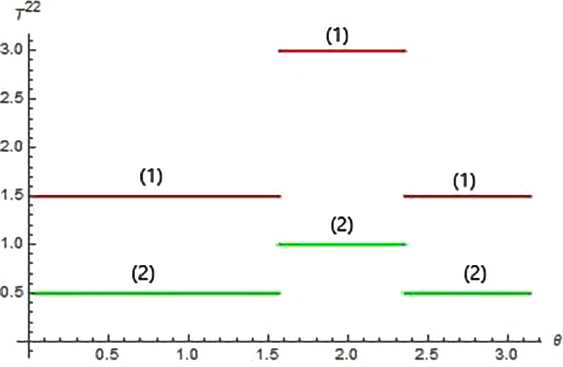
Рис. 4. Усилие Т 22, при R = 3, дз = 1 - линия (1), R = 2, дз == 0.5 - линия (2)