Метод решения некоторых многомерных обратных граничных задач параболического типа без начальных условий

Обратные задачи определения неизвестных граничных условий для параболических уравнений возникают в прикладных задачах в ситуациях, когда на одной части границы известна функция, являющаяся решением уравнения, и ее производная по направлению нормали, а на других ее участках эти характеристики не могут быть определены. К таким задачам относятся, например, задачи теплопроводности, рассмотренные в работе [1], а также модель роста зародышей новой фазы в многокомпонентном растворе в процессе нанокристаллизации твердого аморфного сплава [2]. Как правило, решение этих обратных граничных задач осуществляется при известных начальных условиях. Вместе с тем, существует целый ряд прикладных исследований, при проведении которых невозможно определить начальные условия. К таким задачам относятся, например, исследование электромагнитных и тепловых характеристик работающих двигателей и энергетических установок [3, 4], задачи геофизики, связанные с нагревом и охлаждением поверхности мирового океана [5]. При описании этих процессов и возникают обратные граничные задачи с неизвестными начальными условиями.

Данная статья посвящена разработке численного метода решения такого рода задач. Разработка и исследование методов решения обратных граничных задач является динамично развивающейся областью научных знаний. Основополагающие принципы исследований в этой сфере были сформулированы в работах [6–8]. В настоящее время с этим научным направлением связаны труды многих исследователей. Так, например, в работе [9] рассмотрены итерационные регу-ляризирующие алгоритмы, в статье [10] представлены методы регуляризации в банаховых пространствах, в работе [11] предложен нелинейный метод проекционной регуляризации. Построению алгоритмов решения обратных граничных задач, основанных на использовании метода Треффица, посвящены работы [12, 13]. Методам решения обратной задачи теплопроводности с неподвижной границей, основанным на применении преобразований Лапласа, посвящены работы [14, 15].

В данной статье указана принципиальная возможность построения метода решения и предложена вычислительная схема метода, с помощью которой впервые построено численное решение обратной граничной задачи с неизвестными начальными условиями. В статье приведены результаты вычислительного эксперимента, свидетельствующие о достаточной устойчивости полученных решений.

Постановка задачи

Пусть Q с Rⁿ - замкнутое, ограниченное, выпуклое множество с кусочно-гладкой границей дQ , а Г с дП и Q T = Qx (0; T ) для всех T >  0 . Обозначим

д            д2   Л д

A =д "^ 1 j ^x ■ t ) a x^ jjj x • ¹ ) aj"c ⁽ x ’ t ) .                                ⁽¹⁾

Предположим, что выполнены условия aij (x, t) e C 1(QT), bj (x, t) e C(QT), i, j = 1..n, c(x, t) e C(QT) и для любых (x, t) e QT справедливо n1 I 5 |2< aij (x, t)£i5j < П2 I 5 |2, где n1, П — фиксированные числа, а £ = (^.^n) - произвольный вещественный вектор. Рассмот- рим уравнение:

Au = f ,(2)

где и ( x , t ) e H ^4,2( Q_T ), функция f ( x , t ) e H ^2,1( Rⁿ x [0, T ]), и граничные условия:

, x ,ди , и (x, t )1г=ф( x, t), — 1г = ф( x, t),(3)

ди где ф( x, t), ф( x, t) e H 4,2(QT), ап - вектор нормали. Задача состоит в том, чтобы найти функцию, удовлетворяющую (2), (3), а также найти граничную функцию и (x, t )к=ф( x, t)•

Предположим, что при некоторых f ( x , t ) = f 0 ( x , t ) , ф ( x , t ) = ф ₀( x , t ) и ф ( x , t ) = ф ₀( x , t ) существует функция и o ( x , t ) , удовлетворяющая (2), (3), и известно, что ф ( x , t ) e H ^{2,1 +e} ( Q_T ), где в e (0,1) . Из результатов, представленных в [16, 17] следует единственность решения задачи (2)(4) в некоторой области Q _T с Q T . Для решения задачи (2)-(4) предлагается применить метод дискретной регуляризации.

Метод дискретной регуляризации

Предположим, что существуют Ф , в , R >  0 такие, что

{ maxЬ^{2 u} |, maxЬ^{2 u} |, max x ^u } <  ^R .

max | и ( x , y , t )| < Ф e ^в t , Q _T

В данной статье изложена идея метода дискретной регуляризации многомерных задач, которая заключается в следующем.

В области Q_T вместо исходного уравнения (2) рассмотрим уравнение

Аи + а и = f, где а - параметр регуляризации. Обозначим координаты точки (x, t) e QT как (xi, t) = (x1, x 2,., xn, t) и введем в области QT конечно-разностную сетку из узлов (xk, ts) = (xi, x 2,., xn, ts), i = 1, n, k = 1, N, k = 1, Nt, где индексы (ki, s) соответствуют узлу сетки. Далее, следуя подходу, предложенному Самарским в работе [18], составляем конечноразностный аналог частных производных по каждой переменной в каждом узле сетки (xiki ,ts) . Затем, используя явные схемы, определяем значение функции в точке (xki+1, ts).

Схема легко реализуется как для Q с R , так и на Q с Rⁿ . Для краткости изложения остановимся на рассмотрении схемы метода для Q = [0, X ] x [0, Y ] задачи (2)-(4), имеющей вид:

и, = a(x, y, t) (uxx + uyy ) + f(x, y, tX (x, y, t )e QT,(6)

и(x,0,t) = ф(x,t),Uy (x,0,t) = ф(x,t), (x,t)e Mx, u (0 y^ t ) = g (y^ t) ^               (y, t )e My, где Mx ={(x,t):(x,t)e(0,X)x(0,T)} и My ={(y,t):(y,t)e(0,Y)x(0,T)}, а коэффициент a (x, У, t )e C ( Qt ).

Вместо точных значений функций ф ( x , t ) , ф ( x , t ) , g ( y , t ) и даны некоторые приближения ф_б ( x , t ) , ф₅ ( x , t ) , g _б ( y , t ) и уровень погрешности б >  0 такие, что в каждой точке области уклонение функций ф б ( x , t ) , ф_б ( x , t ) , g б ( y , t ) , от соответствующих ф ( x , t ) , ф ( x , t ) , g ( y , t ) не превосходит б, а именно:

max | ф ( x , t ) -ф б ( x , t )| <б ,   max | ф ( x , t ) -ф₅ ( x , t )| < б ,                                       (9)

(x, t )eMx                                 (x, t )e Mx max | g (y, t) - gб (y, t)<6,                                                                            (10)

⁽ y , t ^{) e} M y

Требуется по этим исходным данным найти u ( x , y , t ) , являющуюся решением задачи (6)–(8) при ( x , y , t ) e Q_T , граничную функцию u ( x , Y , t ) при ( x , t ) e M_x , а также ф ( t ) = u ( x , Y , t ) для всех t e [ 0, T ] .

Заметим, что предложенный численный метод может быть применен для решения обратной граничной задачи для параболического уравнения с погрешностями во всех исходных данных. Тем не менее, выбор именно такой задачи для рассмотрения связан с тем, что с одной стороны, реализация предложенного численного метода для этого уравнения является достаточно простой, а с другой стороны, позволяет наглядно продемонстрировать особенности рассматриваемого численного метода, проверить теоретические результаты и получить экспериментальные значения соотношений между погрешностью исходных данных, величинами шагов и параметра регуляризации.

Численная схема метода дискретной регуляризации

Введем конечно-разностную сетку G в прямоугольнике Q_T ,

G =          ( ^x i , y j , t j ) ^{: x} = ⁽ i ^- 1) h x , y = ( j - 1 ) h y , t = ⁽ k - 1) h t ,

[ h_x = X / N_x ; h_y = Y / N_y ; h_t = T / N t ; i = 1,., N_x + 1; k = 1,., N t + 1, где h_x , h_y и h_t – шаги сетки по переменным x , y и t соответственно.

Следуя подходу, предложенному Самарским в работе [18], конечно-разностный аналог частных производных в каждой точке ( x i , y j -, t_k ) e G определен следующим образом:

vxxj,k = vi+1,j,k - 2Vijk + v-ij,k , i = 2,Nx, j = 2, Ny + 1, k = 1, Nt +1, hx viyk = vi,j+i,k - 2V2j,k + vi,j-1,k , i = 1, Nx +1, j = 2-Ny, k = 1, Nt +1 ,                             (11)

hy vt, j, k = vi, j, k+1 - vi, j, k , i = i,N-+I, j = 2,NyT1, k = 1,Nt. ht

Обозначим через f_t j _k значения функции f e C ( Q_T ) в точках ( x i , y j -, t_k ) e G , значения коэффициентов оператора A обозначим a_{i , j , k} , а значения граничных функций ф ( x , t ) , y ( x , t ), g ⁽ y , t ), q ⁽ y , t ) обозначим ф ,_;k , ф i , k , g j , k , q j , k .

Конечно-разностный аналог уравнения (6) имеет вид:

vi,j,k = a,j,k (vxxj,k + vy/’k)+fi,j,k, k = 1, Nt, vi-j’Nt +1 = Yai,j,Nt +1 [vx^’Nt+1 + VyNt+1 ] + (1 - Y)ai j,Nt [v^’Nt + VyNt ] + fi,j,Nt +1 , где i = 2, Nx +1, j = 2, Ny +1.

Известно, что приведенная схема неустойчива, поэтому мы введем в (6) слагаемое a v i j к и выразим из этих уравнений величины v i j _{+ 1} к . Тогда при i = 2,.., N_x + 1, j = 2,.., N y + 1 получим:

v i , j + 1, к    ² v i , j , к

—

v i , j — 1, к

—

h y ²

a i , j , k

i, j,k , j , i, j ,k xx

—

^{V i} ’ j ’ ^{к + f}! , j , к ^+a v i , j , к ^] ’ ^к = 1, ^N t ’

v i , j + 1, N t + 1 = ^{2 v} i , j , N t + 1

—

v i , j — 1, N, + 1 ⁺ t a

h y ²

¹ i , j , N t + 1

V- j ', N + 1 i , j , N t + 1 v xx

—

v i , j , N t ^{+ 1}

fi , j , N t + 1    ^{a v} i, j , N t + 1

—

(1 — Y ) h y

^Y a i, j , N t + 1

i , j , N_t                     i , j , N_t

’, N t v xx     ⁺ a i , j , N_t + 1 ^v yy

Уравнения (12), (13) эквивалентны добавлению слагаемого

a u

в уравнение (2). Таким обра-

зом, получаем итерационный процесс, позволяющий вычислять неизвестные значения vi j+1 к по следовательно при всех j = 2, Ny +1, к = 1, Nt +1.

Алгоритмические особенности метода дискретной регуляризации

Наиболее существенной особенностью метода является то, что величины N_x и N_y принимают небольшие значения. Такой вывод можно сделать, используя подход, принятый в теории регуляризации [19].

Определим функцию w_i следующим образом:

wj = mi1 aXvi,j+1,к — vi,j,к I’     j = 2-Ny + 1, где vi, j,k удовлетворяет (12), (13). Учитывая (9) и (10), получаем следующую оценку:

W <  (W + 8 ) h_y ,

где W = max |^ik |, i = 1, Nx +1, к = 1, Nt +1. Обозначим m = min|ai j к|. Имеем: i,k                                                                                                                  i, j,k vi, j+1, к    vi, j, к    ( vi, j, к   vi, j—1, к )+         ( vt        ai, j, kvxx      avi, j, к    fi, j, к )

a i , j , k

= ⁽ v i , j , к ^— v i , j — 1, к ^{) +}

h y ² h y ²

v i , j , к ⁺

hx2    ai,j,kht hy                 hy    ai, j, к /                    \               г

+        ,  vi, j, к+1               .2  (vi+1, j, к + vi—1, j, к ) + a vi, j, к + fi, j, к ai,j,kht              ai,j,к L hx

Полагая F = max | f^ j _к |, из последнего соотношения и условий (5) следует i , j , k ⁱ , ^j ,

W j _{+ 1} <  W j +

4 h l ₊ 2 - h i ₊ ^a h l ^h x ²

mht

m

h2

Ф e ^e t + ^FF .

m

h y ²        y

Полагая C = 4^- + 2^- h x ²

h

mht

a h 2                                  h y            --------

+ — y , получаем w j _{+ 1} <  w j + C Ф e ^e t +— F при j = 2, N y + 1. Учиты- m                          m^y

вая (14), получаем

^W N_y + 1 <  Wh y +5 ^h y + ( ^N y

—

. Г             //2)

1) C Ф ee t + h^F.

’m

V

Согласуем величину C так, что с уровнем погрешности 8 и N_y так, чтобы при численной реализации метода дискретной регуляризации вычислительной схемы гарантировано было выполнено условие w_N + 1 <  L 8 для некоторого L >  0 .

Это условие будет выполнено, если имеет место следующее соотношение:

C <Ф e ^{—e 1}

' L 8 — Why +8 5у

,   (N,—1)

—

-F F .

m

С другой стороны,

L 8 — Wh, +8 h Nv < 1 + m-----x.

^у       mC Ф e ^{e z} + h² F

Из (15), (16) следует, что величина N_y может принимать только небольшие значения.

Вычислительный эксперимент

С целью оценки эффективности предложенной вычислительной схемы был проведен вычислительный эксперимент при дополнительном условии u ( X , у , t ) = q ( у , t ) . Эксперимент проводился при разных уровнях погрешности 8 . В качестве тестовых функций выбирались решения следующей прямой задачи:

u t = a ^{( x} , у , ^{t )( u} xx ^{+ и} уу ),      ( x , у , ^t ) е Q T ,

u ( x ,0, t ) = ф ( x , t ) , М у ( x ,0, t ) = v ( x , t ) ,      ( x , t ) e M x ,

u ( ^X , у , г ¹ ) = q ( у , Z ¹) u ( 0, у , t ) = g ( у , t ) , u ( X , у , t ) = q ( у , t ) , ( у , t ) e М у .

Решения этой задачи можно находить с помощью различных известных численных методов. Получив решение этой задачи и используя конечномерный аналог для u_y ( x ,0, t ) , находим у ( t ) • Далее, выберем величины параметров разбиения по пространственным переменным в соответст- ^h y ^{2         h} y ²

вии с величиной h_t , соблюдая условия —— < 1 и -^ < 1, тогда количество узлов по пространст- mh      h ²

x венным переменным определим по формулам X = Nxhx и Y = Nyhy. Основные этапы вычислительного эксперимента состоят в следующем:

Шаг 1 . Моделирование тестовых функций. В качестве тестовых функций выбираются решения прямой задачи (17)–(19). Для ее численного решения используют метод конечных разностей. Величины шагов дискретизации по каждой переменной выбирают так, чтобы обеспечить устойчивость вычислительной схемы решения задачи (6)–(8). Далее, используя конечно-разностные аппроксимации, моделируем значения функции v ( x , t ) .

Шаг 2. Моделирование возмущенных исходных данных ф₈ ( x , t ) , v₈ ( x , t ) , g ₈ ( у , t ) и q ₈ ( у , t ) . Для этого к точным значениям граничных функций добавляем аддитивный шум следующим образом. Значения ф₈ ( x i , t k ) , v₈ ( x i , t k ) в каждом узле сетки ( x i ,0, t k ) вычисляем по формулам:

Ф 8 ( xi , 4 ) = Ф ⁽ xi , 4 ) + Ф err ⁽ xi , 4 X g 8 ⁽ x i , 4 ) = g ⁽ x i , 4 ) + g err ⁽ x i , ч );

V 8 ⁽ x i , 4 ) = V ⁽ x i , 4 ) + V err ⁽ x i , ^t k ), q 8 ⁽ xi, 4 ) = q ⁽ x i , 4 ) + q err ⁽ x i , 4 ),

где функции ф _err ( x , t ) , v _err ( x , t ) , g err ( у , t ) и q_err ( у , t ) являются значениями равномерно распределенных на [ —8 , 8 ] случайных величин.

Шаг 3. Величины параметров разбиения по пространственным переменным выберем в соот-

5 2 <  1.

h x ²

h y ²     1

ветствии с величиной h_t , отношениями и соблюдая следующие условия: —— < —, mh_t 2

Выбор параметра регуляризации а согласуем с уровнем погрешности 8 , параметром 5_у и величиной m , используя величину C и условие (15).

Шаг 4 . Построение регуляризованного решения в точках ( x ,0 + h y , t ). С этой целью используем (7), получаем:

^{и (} x , 0, t k ) = ^u_l^ ,k = Ф i . k , u ⁽ x ^{,0 +} h y , t k ) U ,2, k = Ф i . k ⁺ V i , k h y .

Шаг 5 . Решаем задачу (6)–(8) в оставшихся узлах сетки, используя итерационный процесс, основанный на вычислительной схеме (12), (13). На каждом новом шаге итерационного процесса находим и ( x , y + h y , t ) = и ( x i , y j- _{+ 1}, t k ) по пространственной переменной y при каждом j = 2, N + 1 и k = 1, N + 1.

yt

Предложенная схема была реализована для серии тестовых функций при постоянных и переменных коэффициентах a ( x , y , t ) . В каждой серии проводилось по несколько повторных расчетов для каждой функции. В статье приведены результаты вычислительных экспериментов для коэффициентов a ( x , y , t ) = 1 и a ( x , y , t ) = 1 + 022( x + y + t ) . Во всех тестах мы полагаем X = 1,5 и Y = 1, а T = 2 и, соответственно ^ = { ( x , y ) : ( x , y ) e [ 0,1.5 ] x [ 0,1 ] } , множества

M x = { ( ^x , t ) : ( x , у ) e [ 0,1.5 ] x [ 0,2 ] } и M y = { ( y , t ) : ( y , t ) e [ 0,1 ] x [ 0,2 ] } , а Q t = Qx [ 0,2 ] .

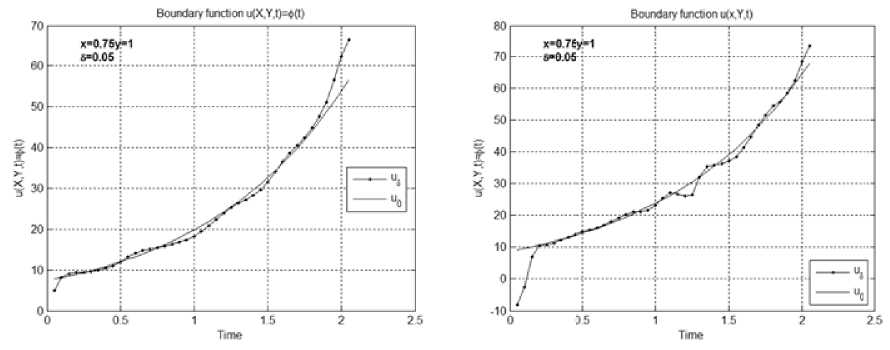
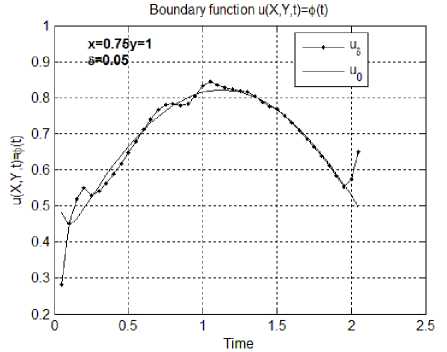
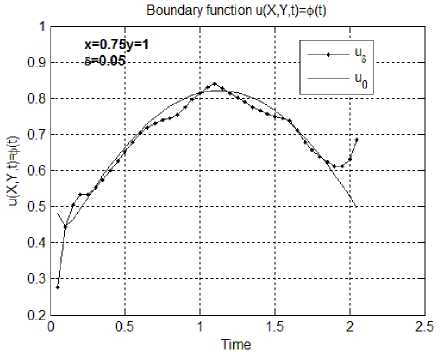
Результаты вычислительного эксперимента для некоторых тестовых функций проиллюстрированы на нижеприведенных рисунках. На всех рисунках используются одинаковые обозначения. Одномерные графики демонстрируют результаты вычислений граничной функции и (0.75,1, t ) = ф (0.75, t ) . Величина погрешности исходных данных, при которой проводились расчеты, обозначена 5. Обозначение и 0 соответствует точному значению тестовой функции и (0.75,1, t ) = ф (0.75, t ) , а и ₅ - численному решению, полученному в точках (0.75,1, t ) методом дискретной регуляризации. Выбор этих одномерных графиков в качестве иллюстративных связан с тем, что значения функции в этих точках (0,75,1, t ) являются наиболее удаленными от известных граничных условий.

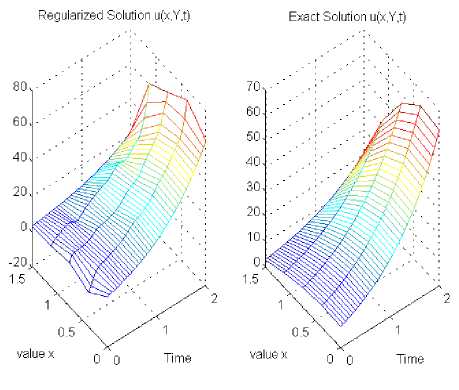
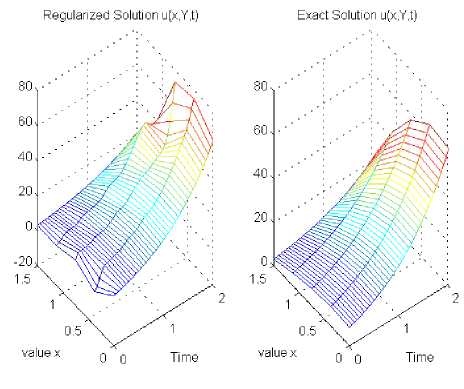
Двумерные поверхности, названные "Exact solution" изображают графики тестовой функций u ( x , y , t ) а поверхности, названные "Regularized solution" соответствуют численному решению и ₅ ( x , y , t ) задачи (6)-(8) в точках ( x ,1, t ) при ( x , t ) е M_x . Ось абсцисс соответствует значениям пространственной переменной x е [0,1.5] , ось ординат - переменной t е [0,2] , а ось аппликат связана со значениями функций и ( x ,1, t ) и и ₅ ( x ,1, t ) . Как одномерные, так и двумерные рисунки (а) соответствуют решению задачи, полученному при a ( x , y , t ) = 1 , а рисунки (б) - решению задачи, полученному при a ( x , y , t ) = 1 + 0.22( x + y + 1 ) .

Пример 1. В этой серии экспериментов в качестве тестовых функций рассматривают непрерывно дифференцируемые, возрастающие по времени, не монотонные по пространственным переменным функции. На рис. 1, а, б изображены результаты численного решения, полученные в точках (0.75,1, t ) для ф ( x , t ) = 26/3 e¹ • cos( x -n /12) , v ( x , t ) = 5 e t • cos( x -n /12) , g ( y , t ) = e t • cos( y -n /6) и q ( y , t ) = 1/3 e t • cos( y -n /6) . Двумерные поверхности "Regularized solution", изображенные на рис. 2, a, б изображают граничные поверхности численного решения и ( x ,1, t ) , полученные для всех точек ( x , t ) е M_x .

Пример 2 . В этой серии экспериментов в качестве тестовых функций рассматривают непрерывные функции, убывающие по времени и имеющие ограниченные производные по пространственным переменным. На рис. 3, а, б изображены результаты численного решения задачи (6)– (8), полученные в точках (0.75,1, t ) для тестовых функций ф ( x , t ) = 26/3 e ^- t • cos( x -n /12) , V ( x , t ) = 5 e ^- t • cos( x - pi /12) , g ( y , t ) = e ^- t • cos( y -n /6) и q ( y , t ) = 1/3 e ^- t • cos( y -n /6) .

а)

б)

Рис. 1. Результаты численного решения задачи (6)–(8) в точках (0.75, 1, t ) для тестовых функций из примера 1

а)

б)

Рис. 2. Результаты численного решения задачи (6)–(8) в точках ( x ,1, t ) для тестовых функций из примера 1

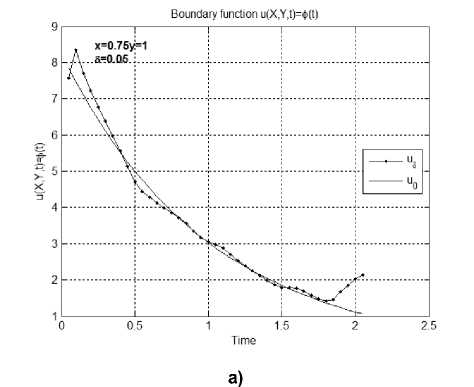
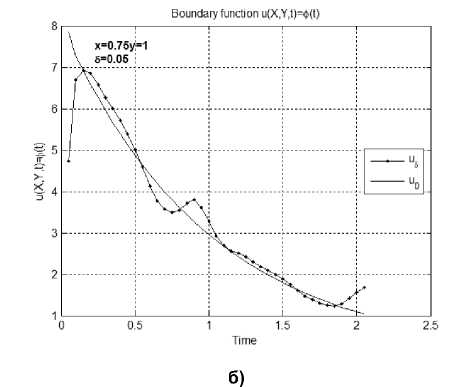
Рис. 3. Результаты численного решения задачи (6)–(8) в точках (0.75,1, t ) для тестовых функций из примера 2

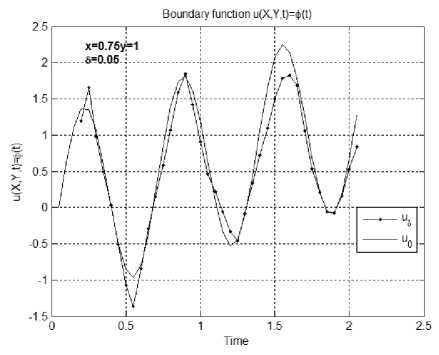
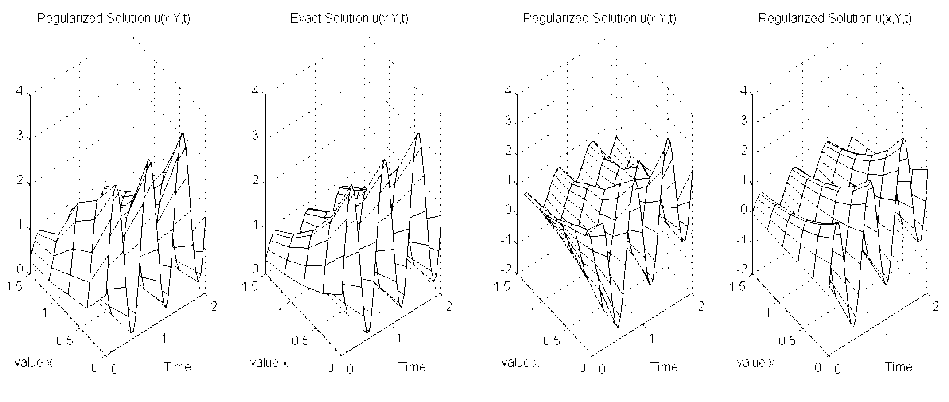
Пример 3 . В этой серии экспериментов построены решения задачи (6)–(8) для тестовых функций, имеющих ограниченную производную по переменной, характеризующей время, и монотонные производные по пространственным переменным. На рис. 4, а, б изображены результаты численного решения задачи (6)–(8), полученные в точках (0.75,1, t ) для тестовых функций ф ( x , t ) = v ( x , t ) = e - x (sin(3 n t ) + t /2) , g ( y , t ) = e y (sin(3 n t ) + t /2) q ( y , t ) = e^{y - 3/2}(sin(3 n t ) + t /2) в точках (075,1, t ) . Рис. 5, a, б иллюстрируют граничные поверхности u ( x ,1, t ) численного решения задачи (6)-(8), полученные при a ( x , y , t ) = 1 и a ( x , y , t ) = 1 + 0.22( x + y + t ) соответственно.

а)

Рис. 4. Результаты численного решения задачи (6)–(8) в точках (0.75,1, t ) для функций из примера 3

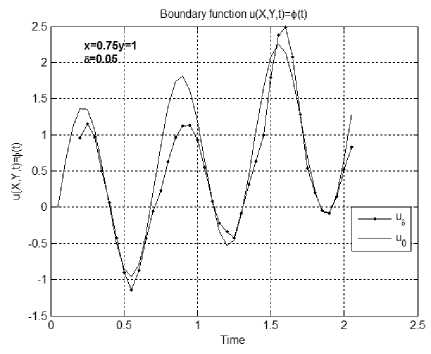
б)

а)

б)

Рис. 5. Результаты численного решения задачи (6)–(8) в точках ( x ,1, t ) для тестовых функций из примера 3

Пример 4. В этой серии экспериментов качестве тестовых функций рассматривают непрерывные функции, имеющие ограниченные производные по времени и пространственным переменным. На рис. 6 а, б изображены результаты решения задачи (6)–(8) в точках (0.75,1, t ) , полученные для тестовых функций

ф ( x , t ) = 0.43(cos( x - 1 + n /12) - cos( x + 1 + 5n /12)),

ф(x, t) = 0.5(cos(x +1 + 5n /12) - cos(x -1 -n /12)), g (y, t) = 0.35(sin(y +1) - sin(y -1)) и q (y, t) = 0.9(sin( y +1) - sin( y -1)).

а)

б)

Рис. 6. Результаты численного решения задачи (6)–(8) в точках (0.75,1, t ) для функций из примера 4

С целью проведения сравнительного анализа точности численных методов в каждой серии экспериментов были найдены величины Δ C = uδC - φ0 и ΔV = uδV - φ0 , где uδC – решение, построенное с использованием метода дискретной регуляризации для уравнения с постоянным коэффициентом, а uδV с использованием метода дискретной регуляризации для уравнения с пе- ременным коэффициентом, а φ0 – значение тестовой функции в точках (0.75,1, t) . Средние значения этих величин, полученных в каждой серии эксперимента для некоторых значений δ , представлены в таблице.

Экспериментальные оценки погрешностей

δ	Тестовая функция примера 1		Тестовая функция примера 2		Тестовая функция примера 3		Тестовая функция примера 4
	Δ C	Δ V	Δ C	Δ V	Δ C	Δ V	Δ C	Δ V
0,01	0,191	0,341	0,217	0,235	0,081	0,103	0,187	0,193
0,03	0,374	0,603	0,390	0,415	0,034	0,037	0,342	0,371
0,05	0,572	0,893	0,602	0,673	0,051	0,056	0,532	0,546

Заключение

В статье предложен метод решения обратных граничных задач с неизвестными начальными условиями, основанный на применении явных разностных схем. Этот метод позволил не только найти неизвестную граничную функцию, но и построить численное решение обратной граничной задачи во всей рассматриваемой области при неизвестных начальных условиях. На основании предложенной схемы был проведен вычислительный эксперимент. Результаты эксперимента свидетельствуют о достаточной эффективности метода, а экспериментальные оценки погрешности численных решений подтверждают устойчивость метода в соответствующей области.