Метод решения однородного интегрального уравнения с разностным ядром для плотности зарядов в преобразователе на поверхностных акустических волнах

Преобразователи на поверхностных акустических волнах (ПАВ) в последние годы находят все большее применение в качестве миниатюрных фильтров, линий задержки и измерительных преобразователей в системах радиолокации, радионавигации и в системах управления.

Основным элементом преобразователя на ПАВ является встречно-штыревой преобразователь (ВШП). Структура ВШП обычно представляется совокупностью идеально проводящих бесконечно тонких металлических электродов с произвольно чередующейся полярностью, произвольно меняющимся периодом и перекрытием соседних электродов на поверхности однородного упругого кристалла бесконечной длины, обладающего пьезоэлектрическими свойствами и граничащего с вакуумом (см. рисунок).

На рисунке слева подключен источник напряжения вида U ПАВ = U 0 exp( - j to t ), где U 0 — амплитуда, ω — круговая частота источника напряжения. Акустические волны, порождаемые приложенным к пьезоэлектрику напряжением, имеют эффективное волновое число k_z , пропорциональное круговой частоте k z = to / c z , где c z = const. — эффективная скорость перемещения фазы (фазовая скорость) поверхностной волны вдоль оси O z .

Если структура ВШП нанесена на деформируемый чувствительный элемент, то при деформации изменяются расстояние между электродами (период) ВШП, механические напряжения в кристалле и как следствие — эффективное волновое число. Этот эффект используется при создании различных измерительных преобразователей физических параметров.

При этом предполагается, что длина электродов (в направлении распространения поверхностной волны) в 40 - 100 раз больше длины поверхностной волны.

Динамичное развитие теории возбуждения ПАВ прошло ряд этапов. Физически и теоретически более обоснованным является решение задачи о возбуждении ПАВ на основе функции Грина,

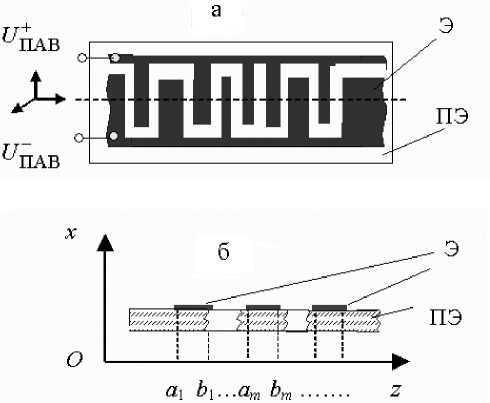
Встречно-штыревой преобразователь поверхностных акустических волн в проекциях на горизонтальную (а) и вертикальную (б) плоскости:

ПЭ — пьезоэлектрик; Э — электроды ВШП; a m , b _m — координаты начала и конца m -го электрода (по ширине)

наиболее корректное вычисление которой произведено в работе [2]. Там же содержится и подробный обзор публикаций, посвященных моделированию ПАВ:

• -    расчету распределения заряда под электродами ВШП в приближении слабой связи ПАВ с пьезоэлектриком;

• -    моделированию взаимодействия ПАВ с системой металлических электродов, когда исходная задача о распределении заряда под электродами сводится к неоднородному интегральному уравнению Фредгольма второго рода, учитывающего влияние генерации ПАВ и объемных волн;

• -    выводу интегрального уравнения для поверхностного распределения тангенциальной составляющей напряженности электрического поля, решение которого ищется в виде итерационного ряда;

• -    определению распределения заряда на основе решения системы алгебраических уравнений, связывающих поверхностный потенциал под каждым электродом с плотностью заряда в конечном числе точек данного электрода.

При решении задачи о распределении заряда на электродах ВШП ранее не учитывалось неразрывное изменение амплитуды волн, либо использовалась только часть функции Грина [2], либо некорректно определялась область существования полученных моделей. Поэтому модель функции Грина нуждается в уточнении области ее определения, а однородное интегральное уравнение для плотности зарядов под ВШП — в получении решения в замкнутой форме.

Исходные уравнения и граничные условия, необходимые для построения моделей функции Грина и распределения поверхностных зарядов, аналогичны уравнениям, обычно используемым при решении задачи о возбуждении акустических волн [2].

Предположение о том, что длина электродов много больше длины поверхностной волны, позволяет решать задачу распределения зарядов под электродом так, как если бы электрод имел бесконечно большую длину.

В статье ставится задача уточнения области определения функции Грина для поверхностных акустических волн, а также получения решения интегрального уравнения для поверхностного распределения тангенциальной составляющей напряженности электрического поля под электродом бесконечно большой длины.

• 1. ОБЛАСТИ ОПРЕДЕЛЕНИЯ ФУНКЦИИ ГРИНА

Связь преобразований Фурье поверхностного потенциала    ф т ( k z )    и точечного заряда

7 _т ( z ) = ст 8 ( z - z ₀) имеет вид [7]

Ф т ⁽ k z ) =

σ

| ^kz| ^£ S ⁽ k z ) ’

где e _S ( k_z ) — эффективная диэлектрическая проницаемость; k_z — эффективное волновое число; ст — поверхностный потенциал заряда в точке ^{( z} = ^z 0 ).

Выполняя обратное преобразование Фурье функции (1), получают

+∞

Ф т ^{( z} 0 ) =7" J

2п J

-∞

exp ^{( -} j kz 0 ) I k z l ^£ S ⁽ k z )

d k_z .

Соотношение (2) фактически определяет функцию Грина точечного источника G ( z ₀) = ф ( z ₀). Поверхностный потенциал, создаваемый произвольным распределением поверхностных зарядов а ( z ), можно найти в соответствии с принципом суперпозиции:

+∞

Ф ^{( z} ) = J G ^{( z} - ^z 0 ) 7 ^{( z} 0 ^{)d z} 0 ,          (3)

-∞ где G(z - z0) — функция Грина точечного источника в точке (z = z0) с единичной плотностью поверхностного заряда (ст = 1):

+∞

G ( z - z 0 ) = — J

2 п ^J

^eX P ^{[ -} j k z ^{( z} - ^z 0 ^)] I k z l ^£ S ⁽ k z )

d k_z .

Для эффективной диэлектрической проницаемости пользуются аппроксимацией Ингебригстена [6]

к ²-ГУ

^£ _s ( k z ) = ^£ S И ,   ,,             (5)

k-k zzS где е,(”) = е,(к)|,   ; ksn,ks — постоянные ве-

SV        S z \k ^^ zS 0 zS личины.

С учетом (5), разлагая дробь под знаком интеграла (4) на простые множители, можно представить функцию Грина потенциала ПАВ в виде суммы двух составляющих — неволновой и волновой:

^{G (} k zS 0 , ^{z - z} 0 ) = ^G C ^{( z - z} 0 ) + ^G K ⁽ k zS 0 , ^{z - z} 0 )» ⁽⁶⁾

где G C ( z - z ₀), G K ( k_{z S 0}, z - z ₀) — неволновая и волновая составляющие функции Грина соответственно.

c               7 ^e xP ^{[ -} j k z ^{( z - z} 0 ^{)] d} kz •

^G C ^{( z z} 0 ) ^G C 0 J                I, I               ;     ⁽⁷⁾

-∞             kz

G K ( k zS 0 , z z 0 )

^+J    k z l

= GK0 J j 2 ,2 exp [-jkz (z - zc)]d kz ;(8)

-L k z ^{- k} zS 0

_____%S . G = ^я zS 0   SS 2n £o ( l ) k ²  ’    K ⁰    2 n E_s ( l ) k ²

SzS0

Интегралы (7) и (8) являются несобственными интегралами, т. е. их значения существуют только как предельные (главные) значения при спрямлении контуров интегрирования.

Главное значение интеграла (7) можно найти с помощью таблиц [3, 5]

+l

G c ( z - z 0 ) = G c 0 J

exp ^{[ - j} k z ^{( z} — ^z 0 ^)] k z

d k_z

+l

= G C 0 J

exp ^{[ - j} k z ^{( z} - ^z 0 ^{)] +} exp [ ^j kz ^{( z} - ^z 0 ^)]

kz dkz

= - 2 G c 0 In | z - z 0| .                                   (9)

Вычислим составляющую (8) функции Грина, воспользовавшись таблицами интегралов [3, 4]. Для этого предварительно приведем интервал интегрирования ( - j , + l ) к интервалу [0, + l ). в результате получим:

при k_zS 0 >  0 и ⁽ z ^- z 0 ) * 0 —

^G K ⁽ k zS 0 , ^{z z} 0 ) ^{_ G} K ⁽ k zS 0 , ^{z z} 0 ) =

^+J      k z l

= G K 0 J , 2 , 2 exp ^{[ - j} kz ^{( z - z} 0 ^{)] d} k z =

• -L k z - k zS 0

_ +p exp ^{[ -} j k z ⁽ z ^{- z} 0 ^{)] +} exp [Jk ^{( z - z} 0 ^)] ,     _

^G K 0 I                    / 2 7 2                     k z ^d k z

0                  kz ^- k zS 0

= ^- G K 0 e ' 0¹ z " z 0¹ Ei ^{( - j} k zS 0 I ^{z - z} 0 I ) ^-

- G K 0 e" j k 0¹ z " z 0¹ Ei ^{( j} k zS 0 I ^{z - z} 0 I ) =

= - ² G K 0 c ^os( k zS 0 I z ^{- z} 0 I ) ci ⁽ k zS 0 I z ^{- z} 0 I ) ^-

^{- 2} G K 0 ^sin( k zS 0 I z ^{- z} <>| ) si ⁽ k zS 0 I z ^{- z} б| );         ⁽¹⁰⁾

при ^k zS 0 ^ ⁰ и ⁽ z - z 0 ) * ⁰ —

^G K ^{( k} zS 0 , ^{z z} 0 ) =

^+J k z l

= ^G K 0 J Vexp ^{[ - j k}z ^{( z - z} 0 ^{)] d} k z = k

-L z

^+j I k I

= ^G K 0 J lex exp ^[ - ^{j k} z ⁽ z - z 0 ^{)] d k} z +

₀ k_z ²

⁰ k_z

^{+ G} K 0 J W^eX p ^[ - ^{j k}z ⁽ z - z 0 ^{)] d k} z =

-L k z

L exp [ ^- j k_z ( z ^- z 0 )] ^- exp[ j k_z ( z ^- z 0 )]

= G K 0 J-----------------7------------------

0                        ^k z

= - j2G K 0 J sin ^{[ j} kz ⁽ z - z ) d k z =

₀           k_z

= ^{- j n g}k 0 sgn ^{( z - z} 0 );

при   k zS 0 * 0 и z ^ z 0 —

G k ( k zS 0, z - z 0) = G k 0 +f -J k z Ld k z = k, - k,_sn

-L z     zS 0

0     I k I                   +l Ъ

= G K 0 J T2 TT^{- d k}z ⁺ G K 0 J "72 zZT" ^{d k}z = ^{0 ;}

• -L ^k z ^{- k} zS 0             0 ^k z - ^k zS 0

при ^k zS 0 <  ⁰ и ⁽ z - z 0 ) * ⁰ —

G K ^{( k} zS 0 , ^{z z} 0 ) “ G K ^{( k} zS 0 , ^{z z} 0 ) =

= G K ( ^-| ^k zS 0b ^{z - z} 0 ) =

= - ^{2 G} K 0 cos [| ^k zS 0 ⁽ z - z 0)| ] • [ ^{П j +} ci I ^k zS 0 ⁽ z - z 0)| ] -

^{- 2} G K 0 sin [| k zS 0 ⁽ z - z 0 )| ^] • ^{[ П +} si I ^k zS 0 ⁽ z - z 0 )| ^] = =

= ^{- 2 n j} G K 0 exp ^{[- j}\^k S 0 ^{( z - z} 0 )1 ^{] +}

⁺ G K ( I k zS c| , ^{z - z} 0 ) ,                                   ⁽¹¹⁾

e где Ei(z) = — d p — интегральная показатель-p

-L ная функция;

L cos p ci(z) = - ----d p — интегральный косинус;

z p

L

si(z) = -J sin p dp — z p 1 при z>0; sgn( z) = - 0 при z = 0; -1 при z < 0. интегральный синус;

Заметим, что, как следует из (10), все составляющие (9) - (11) функции Грина при любом знаке k_{zS 0} симметричны относительно оси ординат

G ( k zS 0 , z - z 0 ) = G ( k zS 0,| z - z d )•             (12)

Другими словами, функция Грина

G ( k_{zS 0}, z - z ₀) зависит от модуля линейной координаты ( z - z ₀) и значения параметра k_{zS 0}. Полученные формы (10) - (11) представления функции Грина соответствуют [2], но отличаются областями значений аргумента ( z - z ₀) и параметра k_{zS 0}.

2. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ ПОВЕРХНОСТНОГО ЗАРЯДА НА ЭЛЕКТРОДАХ ВСТРЕЧНО-ШТЫРЕВОГО ПРЕОБРАЗОВАТЕЛЯ

= J_ J 3 G K ⁽ k „z z . ) J ( z d.        ₀₆₎

i to ^j d z

J -TO

Уравнение для плотности J ( z ) получают на основе граничного значения тангенциальной компоненты напряженности электрического поля на поверхности ВШП

E C ( у = 0, z ) + E K ( у = 0, z ) = 0,       (13)

где E C ( у = 0, z ) — составляющая тангенциальной компоненты напряженности электрического поля, соответствующая системе зарядовых полос на поверхности электродов в электростатическом приближении; E K ( у = 0, z ) — составляющая результирующей тангенциальной компоненты напряженности электрического поля, соответствующая системе акустических волн на поверхности пьезоэлектрика.

При моделировании плотности распределения зарядов в первом приближении можно пренебречь отражением от электродов и обратным преобразованием ПАВ [2]. При этом величины E C ( у = 0, z ) и E K ( у = 0, z ) на поверхности электродов связаны с потенциалом поверхностного заряда соотношением

E C ( z ) = Э фto ^- ) _; E^ z ) = 8ф^ ,  (14)

d z                  d z где

1 j to

1 j to

С учетом (15) - (16) граничное условие (13) можно привести к интегральному уравнению с разностным ядром относительно искомой плотности распределения поверхностного заряда J ( z ₀)

1 то

-1

i to^J

J - то

- 2 G c 0 + d G k ( k s 0 , z - z 0 )

I z ^- z 0I            d z

J ( z c )d z 0 = 0.

Ф с ^{( to} , z )

Ф к ( ^to , z )

J G c ^{( z - z} 0 ) J ^{( z} 0 ) ^{d z} 0 ;

-TO

TO

J G K ⁽ k zS 0 , ^{z - z} 0 ) ^{J ( z} 0 ) ^{d z} 0 ;

-TO

Ф _с ( to , z ), ф _к ( to , z ) — неволновая и волновая составляющие потенциала поверхностного заряда соответственно; G_c ( z - z ₀ ), G_K ( k_{S 0} , z - z ₀) — неволновая и волновая составляющие функции Грина, соответствующие формулам (9) - (11).

Подставляя (9) в (14), получим:

EC(z) д Фс(to .z) = zd

=jlrG:лdzo = ito 2d

J —TO

TO 1

= —- Ji-----1J(z0) dz0,(15)

j to -TO | z - z 0I

EK(z) = 3 Фкto z = zd

Первый член в уравнении (17) учитывает напряженность электрического поля поверхностных зарядов в электростатическом приближении. Второе слагаемое в уравнении (17) учитывает напряженность электрического поля бегущих волн.

Уравнение (17) является однородным интегрально-разностным уравнением первого рода с разностным ядром, которое может быть представлено в виде суммы двух слагаемых, первое из которых симметрично относительно оси ординат и в каждой полуплоскости является нечетной функцией аргумента, а второе слагаемое имеет первообразную функцию, симметричную относительно оси ординат.

Уравнения типа (17) обычно решают методом последовательных приближений [2]. Даже с использованием компьютера с частотой 2.5 ГГц этот метод требует ощутимых затрат времени на получение достаточно точного решения.

Ускорить расчеты можно, получив выражение для J ( z ) в замкнутом виде. Для этого преобразуем интеграл в уравнении (17) с помощью интегрирования по частям. Согласно (12), функция G_K ( k_{zS 0}, z - z ₀) симметрична относительно оси ординат на плоскости ( ( z - z ₀), G_K ) при любом знаке k_{zS 0}. Как следует из дальнейшего, при условии (12) и распределение плотности заряда J ( z ₀) = J ( - z ₀) также оказывается функцией, симметричной относительно оси ординат. Поэтому на обоих концах интервала интегрирования ( -то , + то ) разность значений произведения G_K ( k_{zS 0}, z - z ₀) J ( z ₀) оказывается равной нулю.

Преобразуем интеграл (16) с учетом того, что d GK(kzS0,z-z0) _ d Gk(ks0,z-z0) = .

d z d z ₀

В результате интегрирования по частям получим

E z^K ( z ) = — J G K ( k s 0 , z - z 0 ) ^ J ^ z ⁰^ d z 0 . (18) i to ^J                        d z_n

-TO                                    0

Чтобы не использовать нелинейную операцию вычисления модуля ( z - z ₀), приведем интеграл (15)

к сумме интегралов по интервалу [0, то ):

то уравнение (21) можно представить:

E^CC ( z ) =

— 2 G c 0 7 j to -L | z

I J ^{( z} о ) ^{d z} 0 ^z o|

-

- 2 G_c о

Г J ( z 0 )

^{j to} zl z - z о|

^d z о ^-

2 G c 0 г J ( z 0)     _

——J I----1d z 0 = jto L |z-zo|

ТО

2 G

—— [ J ( и - z ) + J ( z + и ) ] + u

+ G k ( k zS 0 , и )

d [ J ( и - z ) + J ( z + и ) ]

d и

d и = 0. (23)

^{2 G} C ⁰ f J ⁽ z ^{+ U 1 )} d U 1 ^{j to}   0     ^u 1

2 G.

ТО

^{j to}  0

Jz-^ d и 2 , (19) u 2

где в соответствии с порядком следования интегралов выполнены замены переменных интегрирования z ₀ = z - u и z ₀ = z - и ₂.

Поскольку G K ( k_{zS 0}, - z ₀) также зависит от модуля ( z - z ₀), интеграл (18) также приведем к сумме интегралов по интервалу [0, то ):

х 1 С             ^d J ( z ) я

Ez (z) =— I GK (kzS 0, z - z 0Н--- d z 0 = jto -TO

1 7^/7         A^d J ( z ₀ )

= . I GK(kzS 0,z z 0) Д      d z 0 + jto z

1 Г л             \d J ( z ₀)

+ ~ I GK (kzS 0,z  z 0) 4     d z 0 = jto -TO

_ 1 l'z- /7, A^{d J ( z} + ^и 1 )_д_

. I GK(kzS 0, ^ Д jto b

-—jGk(kzS0,и2)d J(z - u2) dи2 = 0,(20)

jto '

При получении решения уравнения (23) необходимо также учесть ограничение на выбор пути интегрирования, включающего заранее не обусловленные границы электродов. Следовательно, значение верхнего предела интегрирования в (23) должно быть не только достаточно большим, но и произвольным числом. Поэтому интегральноразностное уравнение (23) можно заменить дифференциально-разностным уравнением для подынтегральной функции

- 2 G

----— [ J ( и - z ) + J ( z + и ) ] +

u d Г J (и - z) + J (z + и )1

+ G k ( k zS 0 , и )                           = 0 .       (24)

d и

Решение дифференциально-разностного уравнения (24) при z ^ 0 будем искать в виде суммы экспоненциальных функций:

при k zS 0 >  ⁰ —

[ J ( и - z ) + J ( z + и ) ] ⁺ =

где в соответствии с порядком следования интегралов выполнена замена переменных интегрирования z0 = z + u1, z0 = z - и2. Кроме того, использована замена переменных дифференцирования d = d_ d z 0     d и 2

Подставляя (19) и (20) в (13), получим интегрально-разностное уравнение относительно плотности заряда:

= c ( z ) 1 exp

"7   2 Gc 0 d t

- z t G K ( k zS 0 , t )

+ exp

2 G_{c 0} d t t G K ( k zS 0 , t )

при ^k zS 0 <  ⁰ —

[ J ( и - z ) + J ( z + и ) ] =

7 J ( z - и )_Д   „   JJ ( z + и ),

• -2 Gc 0 -------d и - 2 Gc 0

0 и0 iV          J(z - и)

• - Gk (kzS 0, и)----d

^{д и}

+jGk(kzS0,и)d J(z + и) dи = 0.

'd

Если выполнены условия d J(z - и) =-d J(и - z); J (z - и) = J (и - z), (22) d иd

= ^{c ( z} ) u [f

2 G_{c 0} d t t G K - ( k zS 0 , t )

+ exp

2 G_{c 0}d t t G k ( k zS 0 , t )

где [ J ( и - z ) + J ( z + и ) ] ⁺ , G K ( k zS 0 , t ) и [ J ( и - z ) + J ( z + и ) ] ^- , G K - ( k_{zS 0}, t ) — распределения плотностей зарядов и функции Грина при k_{zS 0} >  0 и при k_{zS 0} <  0 соответственно; c ( z ) — постоянная интегрирования.

Определим c ( z ), исходя из начальных условий: при и = 0 — c ( z ) = J ( - z ) + J ( z );

при z = 0 — C (0) = 2 J (0).

Следовательно, плотность распределения зарядов может быть определена по формулам:

при ^k zS 0 >  ^{0 —}

J ⁺ ( u ± z ) = J ( ± z ) exp

Т   2 G_c 0 d t

±^J t G K ( k S 0 , t )

при ^k zS 0 <  ^{0 —}

J ( u ± z ) = J ( z ) exp

(    2 G c 0 d t

±^J t G_K ( k zS 0 , t )

Поскольку J ± ( u ) = J ± ( - u ), т. е. изменение

знака верхнего предела интегрирования в (27) - (28) не приводит к изменению знака интеграла, то условия (22) выполняются, обеспечивая корректность перехода от интегрального уравнения (17) с разностным ядром к интегральноразностному уравнению (21).

Функции (27) - (28) могут быть использованы в качестве первого приближения при расчете параметров структуры ВШП. Располагая функцией Грина и выражением для плотности распределения поверхностного заряда, можно получить все остальные характеристики поверхностной акустической структуры, например, выражение для проводи-

ю мости УВх (to) = J ^(to,z)J* (z) dz, где УВх (to) —

-^

входная проводимость ВШП для частоты входно-

1 f„, го сигнала to ; ф ( to ,z ) = — G ( z - z ₀) J ( z ₀) d z ₀ j to ^J

-TO

—

поверхностный потенциал; J * ( z ) — сопряженная

величина плотности заряда.

Вычисления сингулярных интегралов (27) - (28) можно еще более упростить, если интегралы пред-

ставить в виде суммы интегралов по конечным

интервалам

V п (V +1) п

2 ’    2

и подынтегральную

функцию на каждом интервале ( v = 2, 3, „.) аппроксимировать дробно-рациональным выражением

t G k ( k zS 0 , t )

^b v

П ( t - t ± m )

« V± m

(t - V, m )

где b _v — постоянный коэффициент; n , t ; _m — соответственно степень и корни полинома, аппроксимирующего функцию t G K ( k_{zS 0}, t ) на интервале

V п (V +1) п

2 ’    2

; t — аргумент полинома; a _{v m} —

коэффициенты разложения левой части выражения (29) на простейшие дроби.

Например, на интервалах

V П (V +1) п

2 ,    2

при

( v > > 1) функция Грина G K (1, | t | ) является почти периодической и хорошо аппроксимируется полиномом не выше четвертой степени, который с точностью до постоянного сомножителя не-

трудно представить в 4 п [ 2 u 1 |          | tv, m , где r 2u m =1 (v п, (v п виде произведения

— дробная часть от

числа 2-u- . V п

Тогда распределение плотности заряда на ин-

тервалах

V П (V +1) п

2 ,    2

ной функции

J ( u ) =

= J

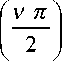
u

будет иметь вид степен-

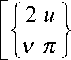
t

V , m

П [-1.,. ]

m = 1

При использовании аппроксимации (29) задача вычисления плотности распределения зарядов под электродами встречно-штыревого преобразователя сводится к вычислению значений произведения (30).

Методы разложения в асимптотические ряды интегралов со степенным ядром типа (30) рассмотрены в [1].

ЗАКЛЮЧЕНИЕ

В работе уточнены области определения функции Грина, используемой при анализе и синтезе преобразователей на поверхностных акустических волнах.

Предложен метод решения интегрального уравнения с разностным ядром для плотности распределения зарядов под электродом бесконечной длины.

Интегральное уравнение с разностным ядром с помощью интегрирования по частям сведено к дифференциально-разностному уравнению, решение которого получено в замкнутой форме.