Метод решения задачи линейного стохастического программирования с несовместными ограничениями
Автор: Щепалов Сергей Владимирович, Кузнецов Владимир Алексеевич
Журнал: Ученые записки Петрозаводского государственного университета @uchzap-petrsu
Рубрика: Прикладная математика и информатика
Статья в выпуске: 2 (107), 2010 года.
Бесплатный доступ
Стохастическое программирование, приближенное решение, стохастическая модель, линейная оптимизация, несовмест- ные ограничения
Короткий адрес: https://sciup.org/14749686
IDR: 14749686
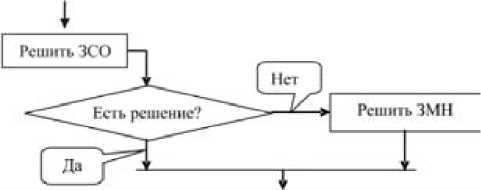
Список литературы Метод решения задачи линейного стохастического программирования с несовместными ограничениями
- Бравый М. Я., Соболев И. В. Опыт решения задачи линейного программирования со случайными технологическими коэффициентами//Математические методы в экономических исследованиях. Сер. «Оптимальное планирование и управление»/Академия наук СССР. М.: Наука, 1974. С. 17-25.
- Воронов А. А. Исследование операций и управление. М.: Наука, 1970. 128 с.
- Воронов Р. В. Генетический алгоритм для задачи линейного раскроя//Тр. ПетрГУ. Сер. «Прикладная математика и информатика». Петрозаводск: Изд-во ПетрГУ, 2007. С. 35-49.
- Соболев И. В. Управление производством пиломатериалов. Петрозаводск: Карелия, 1976. 173 с.
- Фидлер М., Недома Й., Рамик Я. Задачи линейной оптимизации с неточными данными. Ижевск: НИЦ РХД, 2008. 288 с.
- Шерстобитов В. В. Математическое программирование. Ч. 1. Элементы линейной алгебры: Учеб. пособие. Л.: ЛТА им. С. М. Кирова, 1969. 88 с.
Статья
