Метод решения задачи множественного рассеяния электромагнитных волн в однородной безграничной среде

Задаче множественного рассеяния волн, в частности электромагнитных волн, когда в некотором первичном поле находится не менее двух рассеивателей, а их взаимным влиянием друг на друга (вторичным перерассеянием) пренебречь нельзя, посвящено большое число публикаций. Упомянем лишь некоторые из них — [1–15].

Рассмотренная впервые в работе [ 1 ] для взаимодействия двух рассеивающих тел в задаче дифракции на щели проблема множественного рассеяния получила свое значительное развитие. Укажем лишь некоторые методы ее решения.

Так, в работе [ 2 ] дан обзор метода, когда решение ищется в виде суммы первичной волны и результирующих полей всех рассеивателей. На границах рассеивателей накладываются краевые условия и условия излучения на бесконечности для рассеянного поля. В работах [ 3-6 ] рассматривается метод решения задачи множественного рассеяния на объемных рассеивателях путем сведения ее к решению интегральных уравнений. В работе [ 7 ] метод, развитый в работах [ 3-6 ] , применяется для решения соответствующей задачи в плоских волноводах. В работах [ 8-12 ] решение ищется с привлечением теорем сложения для различных решений векторного уравнения Гельмгольца, позволяющих аналитически решать задачу множественного рассеяния. Наконец в работах [ 14, 15 ] рассматриваемая задача решается методом Т-матриц, развитым в работе [ 13 ] для случая одиночного рассеивателя.

В настоящей работе для решения задачи множественного электромагнитного рассеяния на нескольких телах предлагается альтернативный подход, заключающийся в учете многократно переот-раженных (перерассеянных) между телами плоских волн. Учет перерассеянных плоских волн осуществляется с помощью использования невозмущенных матриц рассеяния каждого из тел, что приводит к интегральным уравнениям, позволяющим вычислять возмущенные матрицы рассеяния через невозмущенные. Ранее сходная методика была применена автором при решении аналогичной акустической задачи [16], а также задач расчета результирующего акустического рассеяния протяженных излучателей и рассеивателей в условиях влияния границ раздела и слоистой неоднородности среды [17–19].

Единственное ограничение предлагаемого подхода заключается в том, что должны быть известны невозмущенные матрицы рассеяния тел, однако это требование не представляется чрезмерным, т. к. "паспортом" рассеивателя является именно его матрица рассеяния в условиях однородной безграничной среды при отсутствии посторонних тел.

ПОСТАНОВКА ЗАДАЧИ

Без ограничения общности рассмотрим задачу для вакуума в случае трехмерного неограниченного пространства. Вначале сформулируем математически прямую задачу рассеяния для случая единичного рассеивателя, занимающего ограничен- ную область D с R 3, находящегося в поле первичной электромагнитной плоской волны. Суммарное поле, как обычно, рассматривается в виде суммы падающей ui и рассеянной волны us (i в индексах — признак принадлежности к падающей волне (от "incident")). Обычно рассматриваются две классические постановки прямой задачи рассеяния: а) рассеиватель представляет собой прозрачную ограниченную неоднородную область D с R3; б) рассеиватель представляет собой непрозрачное неоднородное включение, ограниченное поверхностью dD, где dD — граница области D.

Пусть падающая волна имеет вид (временнóй фактор полагаем равным exp( -itot ))

E i^{( x )} = E 0i ^ex P ⁽ i ^k i ^x X

^H i^{( x )} = —^Vx E i^{( x )} = ^k i ^x E 0i ^e xp ⁽ i ^k i ^{x )} .

ik

Здесь и везде i — мнимая единица.

Следуя в основном [20], запишем выражения для падающей (2–4) и рассеянной (5–8) волн:

Vx E - ik H = 0,

Vx H + ikn ( x ) E = 0, x e R 3 ;

E ⁽ x ) = E 0i exp ⁽ i k i x ) + E s⁽ x ),

H ^{( x )} = ki ^x E 0i exp ⁽ i k i x ) + H s ( x );

lim( H _s x x - R E _s) = 0,

R ^~ lim(E s x x + RH s) = 0 .

R ^~

Здесь Ei , Hi и Es , Hs — компоненты падающей и рассеянной электромагнитных волн соответственно; n = e / e0 — показатель преломления; e(x) (xe D) и e0— диэлектрические посто- янные неоднородной среды и окружающего вакуума соответственно (магнитная проницаемость полагается постоянной во всем пространстве x = = (x,y,z) e R3); R = |x|; ki = kki — волновой вектор падающей волны; k = to /c — волновое число; kˆ i — единичный вектор, совпадающий по на- правлению с вектором ki (далее везде вектор с "крышечкой" обозначает единичный вектор); c — скорость света в вакууме; E0i — постоянный вектор поляризации электрического поля падающей плоской волны. Условия излучения Сильвера—Мюллера (4) служат для выделения единственного решения прямой задачи рассеяния, каждое из них является следствием другого (обычно ограничиваются одним из них), и для векторного уравнения Гельмгольца они переходят в условия излучения Зоммерфельда для компонентов векторного поля (см., напр., [21]).

Для рассеянной волны:

Vx E - ikH = 0,(5)

Vx H + ik E = 0,      x e R ³\ D ;

E(x) = E0i exP(ikix) + Es (x),

0i           i          s

H ^{( x )} = k i ^x E 0i exp ⁽ i k i x ) + H s^{( x )} ;

r(E(x), H(x)) = 0,   x edD;(7)

lim( H _s x x - R E _s) = 0,

R ^~ lim(Es xx + RHs) = 0.

Здесь условие (7) символически определяет краевые условия на границе непрозрачного рассеивателя D .

В дальнейшем везде будем полагать, что решения прямых задач рассеяния (2–4) или (5–8) для одиночного рассеивателя существуют и единственны. Расчеты будут вестись для электрической составляющей поля, магнитная составляющая вне рассеивателя может быть найдена из уравнений Максвелла (2)

H = — VxE.

ik

ПРЕДСТАВЛЕНИЯ ПОЛЯ РАССЕЯНИЯ

Пусть для определенности начало координат находится внутри области D . Как известно ([22] для скалярного случая и [23] для случая электромагнитного поля), поле излучателя (рассеивателя), компоненты которого удовлетворяют условиям излучения Зоммерфельда, можно единственным образом представить вне полосы ^ _D = { x , У e R ², z ₂ ^ z ^ z 1 } , включающей этот излучатель, в виде двумерного интеграла Фурье. Здесь z ₁ и z ₂ соответственно максимальная и минимальная аппликаты области D . Используя, к примеру, результаты работы [22], справедливые для решения скалярного уравнения Гельмгольца, легко выписать выражение для векторного потенциала электромагнитного поля рассеяния, являющегося решением векторного уравнения Гельмгольца при произвольном первичном поле

^A s ^{( x )} =     Ja ( k ^ 2 exp ⁽ i k m ^{x )} d k x d k ,

2n   a

R ²

m = 1,2; x e R ³ \ Q _D .

Здесь k 1 = (kx, ky, a) и k 2 = (kx, ky ,-a) — сопря- женные волновые векторы; а = (к2 - kx2 - ky2)1/2; к — волновое число; m = 1 соответствует полю в верхнем полупространстве z > z 1, m = 2 — в нижнем полупространстве z < z2; a(k m) — спектр векторного потенциала.

Если применить к каждой плоской волне в (9) тождество из [ 24 ]

E = ik (A + ^ W * A), то для рассеянного электрического поля получим:

^E 5 =     JTk m ) exp ⁽ i k m ^{x )} d ^kx d ^ky ,

^{2 п} RR 2 ^а                                  (10)

m = 1,2,    xeR 3\QD, где векторы

T ( k m ) = ik ( a ( k m ) +    W * a ( k m ))

k ²

представляют собой векторы, лежащие в плоскости, нормальной к векторам k _m (см., напр., [ 23 ] ). Таким образом, как видно из (10), падающая волна вызывает сплошной спектр плоских рассеянных волн не только однородных k x ² + k y ² <  k , но и неоднородных k x ² + k y ² >  k .

Асимптотическая оценка интегралов (10) при R ^^ в направлении ( 0 , ф ) ( k x ² + k_y ² <  k ² , что соответствует так называемой области видимости), где R = |х| и ( R,0,ф ) — сферические координаты, дает [ 22-24 ]

дальнего поля рассеивателя) [25, 26]. Для определения матрицы рассеяния введем следующие системы координат, связанные с векторами падающей k i и рассеянной k _s плоских волн. Пусть k i и k _s — соответствующие им единичные вектора, тогда остальные два вектора этих систем координат вычисляются следующим образом [ 26 ] :

/X                     /X                                       /X           /X h is = z X k is,        v is = h is X k is, где z — единичный орт вдоль оси OZ ; h — соответствующий горизонтальный орт, лежащий в плоскости, нормальной к k; V — вертикальный орт, лежащий в той же нормальной плоскости. Отметим, что орт h лежит в плоскости, параллельной плоскости k Ok , и действительно явля-xy ется горизонтальным вектором. Впредь подразумеваем, что вектора h и V зависят от вектора k.

Пусть на рассеиватель падает плоская электромагнитная волна вида (1). Разложим вектор E _0i по системе векторов ( h i , v i ):

E 0i = (E 0 h h i + E 0 v Vi), а амплитуду рассеяния по направлению ks по системе векторов (h s, vs)

/X

T ( k s ) = ( T h ( k s ) h 5 + T v ( k s ) V s ).

Тогда, как показано в [ 25, 26 ] , для данного конкретного рассеивателя справедливо следующее матричное равенство:

Г T h ^{( k} • > ]

T (k ) | v v s /у

(T T T ¹¹ T ¹²

T T

I ^T 21 ^T 22

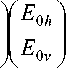
E ' _s ( R , 0 , ф ) = T ' _s ( 0 , ф)^exp(i ^k Rl R

Здесь

T '_s ( 0 , ф ) = T ( k 1 ),

T '_s ( п - 0 , ф ) = T ( k 2 ),

1 + O | — I kR

. (11)

Матрица T ( k i , k _s)

Г ^T„ T ,2 ]

T T

I T 21 T 22 у

называется мат-

рицей рассеяния (мр). Она не зависит от свойств

падающей плоской волны, а зависит только от

/X              /X свойств рассеивателя и векторов k i и k s (отме-

0 e [ 0, п /2 ] , ф е [ 0,2 п ] , а e [ k ,0 ] ; а = k cos 0 ; k x = £ cos ф ; k y = ^ sin ф ; ^ = k sin 0 ; ^ = = ( k x , k y ) = ( 5 , ф ) — горизонтальная проекция волнового вектора. Функция T '_s ( 0 , ф ) носит название амплитуды рассеяния, а ее значение совпадает с весовым множителем в (10) плоской волны, распространяющейся в данном направлении.

Фундаментальную роль в дальнейшем изложении играет матрица рассеяния (характеристика

тим, что речь идет о матрице рассеяния по электрической составляющей поля рассеяния, по магнитной составляющей мр вводится аналогично, и они аналитически связаны). В работе [ 25 ] приведена техника вычисления матриц рассеяния для конкретных рассеивателей.

Таким образом, мр напрямую ассоциируется с откликом рассеивателя на падение плоских волн. Поскольку выражение (10) двузначно зависит от переменных интегрирования k x , k y , обозначим матрицу рассеяния следующим образом: t m ( k i , k s ), n , m = 1,2 . Нижний индекс m = 1,2 ха-

рактеризует направление движения падающей плоской волны: m = 1 — волна движется в сторону возрастания z , (т.е. снизу вверх), m = 2 — наоборот. Индекс n характеризует направление рассеяния n = 1 — рассматривается рассеяние вверх (значение + а ), n = 2 — рассеяние вниз ( - а ). Рассматриваются области определения как внутри, так и вне области видимости.

Для введения необходимого в дальнейшем векторного оператора образуем следующий аффинор A_m ⁿ ( k _i , k _s ) , ассоциированный с мр:

A m ( k i , k s ) =

ˆ nˆ n h s\(^11) m h i + (T12) m v i +

+ v s ( ( t 21 ) m • h i + ( t 22 ) m • V i ).            (12)

Отметим, что все слагаемые зависят от векторов k _i , k _s ; ( T_lj ) ⁿ _m — соответствующие элементы матрицы T m ( k i , k _s), 1 , j = 1,2. После этого легко найти поле рассеяния при падении плоской волны с произвольным вектором поляризации E _0i :

E =     f Am (ki,ks)Eoi exp(ik )dk dk s   2n R2       as               s “ sy   (13)

x e R ³ \ Q D .

Следует обратить внимание, что в (13) и далее имеет значение порядок следования аффинора и вектора вследствие невыполнения коммутативности их произведения в общем случае.

Когда центр рассеивателя смещается из начала координат в точку x ₀ , вследствие линейности задачи отклик на падение плоской волны (1) имеет вид

E s = -i- exp(k i x o) x 2n xJ

R ²

A mⁿ ( k i , k s ) E 0i

^a s

exp( i k _s( x - x ₀))d k _{s x} d k _{s y} ,      (14)

x e R ³ \ Q D .

Пусть центр источника первичного падающего поля находится в начале координат. Тогда электрическое поле источника может быть представлено в виде, аналогичном полю рассеяния (10) [ 22, 23 ] :

^E i =      f ^{D ( k} m ) exP ⁽ i k m x ^{)d k}x ^d k y ,

^{2 n} R 2 ^a                            (15)

m = 1,2; x e R ³\ Q D .

Здесь D ( k _m ) — вектор диаграммы направленности электрического поля, лежащий в нормальной плоскости к вектору k _m . В случае когда рассеиватель с центром в точке x ₀ находится в первичном поле (15), результирующий вектор поляризации рассеянного поля может быть найден с помощью техники, изложенной в [ 16, 17 ] , и имеет вид

^T n ⁽ k s , x o ) =

= г J An(ki,ks)Dm(ki) exp(ikixo)dkixdkiy, (16) 2n R 2        a i n = 1,2.

Здесь для устранения избыточных индексов принято обозначение D _m ( k ) = D ( k _m ) ( D ( k _m ) фигурирует в (15)).

Знание результирующего вектора поляризации рассеянного поля позволяет находить поле рассеивателя в виде

E s = г J ^{T n ( k s}, ^{x o)} exp ⁽ i k s ( x - x o^))d k s x d k s y , ^{2 П} R 2     ^a s                                 (17)

n = 1,2.

Величину T n ( k _s, x ₀) из (16) при переменном x ₀ можно трактовать как некое поле рассеяния, т. к. оно по форме совпадает с (13–15) и удовлетворяет векторному уравнению Гельмгольца. В случае электромагнитных волн, как и в скалярном случае, имеет место полезное разложение из [ 21 ] , которое справедливо в случае выполнения условий (4), (8). А именно любое решение векторного уравнения Гельмгольца вне наименьшей сферы, включающей источник, может быть представлено в виде абсолютно сходящегося ряда

E    = exp( ikR ) у E i ( 0 , Ф )

R     l ^o ( kR ) ¹ ,

E i + 1 ( 0 , ф ) = L [ E i ( 0 , ф )]( 0 , ф, 1 ).          (19)

Здесь L — оператор, определяемый выражением

дтж ф, 1 )

^Л 9 , ф + ¹ ( ¹ + 1) 2 i ( 1 + 1)

W, ф ),

V

позволяет рекурсивно найти все члены ряда (18) по члену с индексом 0, который в свою очередь легко находится с помощью асимптотической оценки интегралов типа (10) и представляющих собой двумерные преобразования Фурье. Как видно из (11), они представляют собой соответствующее значение спектра, представленное в сферической системе координат, поделенное на exp( iaz I)

функцию ------!—. Тогда применительно, на- a пример, к (10) имеем

E о ( 9 , ф ) = T *_s ( 9 , ф ).               (21)

Окончательно для (16) имеем

T '( R о , 9 о , ф о , 9 s , ф s ) =

= ^ex p ⁽ ikR о ) у A i ^{( 9} о , ф о , ⁹ s , Ф s^{)           (22)}

^R о      1 = о       ^{( kR} о ) ¹

A 1 + 1^{( 9} о , ф о , ⁹ s , ф s ) =

= L[ A _z ( 9 о , ф о , 9 s , ф s )]( 9 о , ф о , 1 ),

A о^{( 9} о , ф о , ⁹ s , ф s ) =

= •                                     (24)

= A m ( 9 о , ф о 9 , ф s ) D '( 9 о , ф о ).

Здесь приняты обозначения: ( R _о, 9 _о, ф _о) — сферические координаты точки x _о = ( x _о, у _о, z _о), центра рассеивателя; ( R _s, 9 _s, ф _s) — сферические координаты произвольной точки относительно точки-центра ( x _о, у _о, z _о); Л _9ф — оператор Бельтрами на сфере (угловая часть лапласиана); штрих вверху функции говорит о том, что она рассматривается в соответствующей сферической системе координат.

Представление (22-24) позволяет легко проанализировать ошибки при вычислениях результирующего вектора поляризации в виде конечной суммы. Так, в зоне Фраунгофера можно ограни -читься нулевым приближением

T'(R о,9 о, фо,9 в, ф s) = n т т т \ eXp(ikR о) ,

= A m ^{( 9} о , ^ф о , ⁹ s , ^ф s^{) D ( 9} о , ^фо)    _D ^{+    (25)}

^R о

+ O

IT

что соответствует представлению о том, что поле источника в точке рассеивателя представляет собой плоскую волну с весом n т О            т Cxp(ikR о)

^Am ^{( 9} о , ^ф о , ⁹ s , ^ф s ) ^{D ( 9} о , ^ф о )     _D •

^R о

Если подставить T из (25) в интеграл для поля рассеяния (17), то получаем следующую асимптотику:

E s ( R s , 9 s , ф s ) =

= exp(ikRо) exp(ikRs) у A1 (9s,Фs)

R о        R s ^у ( kR s ) ¹ ’

A1+1 (9s, ф s) = L [A 1 (9s, ф s )](9 s, Фs, 1),(27)

'

Aо(9s,фs) = Amn (9о,фо,9s,фs)D'(9о,фо).(28)

Если теперь уже в (26-28) ограничиться нулевым приближением, то получим лучевую версию рассеяния:

E s ( R s , 9 s , ф s ) =

'

= A mn ( 9 о , ф о , 9 s , ф s ) D '( 9 о , ф о ) x ,        (29)

exp(ikRо) exp(ikRs ) x, R о       Rs а именно, луч, вышедший из направленного источника в сторону рассеивателя под углами 9о, фо в системе координат источника, взвешивается его диаграммой направленности D' (9о, фо), достигает рассеивателя в точке (Rо,9о,фо), отражается под углами 9s, фs относительно рассеивателя, одновременно взвешиваясь мр, и, достигая точки (Rs,9s,фs) в системе координат рассеивателя, приобретает амплитуду (29).

ДВА РАССЕИВАТЕЛЯ В ПОЛЕ ПЛОСКОЙ ВОЛНЫ

Рассмотрим далее случай, когда в однородном пространстве расположено два рассеивателя S 1 и S2 с соответствующими исходными мр (невозмущенными, когда их влияние друг на друга исключено), из которых строятся соответствующие аффиноры 1 Amn (k i, k s) и 2 Amn(k i, k s) (назовем их аффиноры рассеяния (ар)). Пусть центр первого z рассеивателя расположен в точке (о,о,——), вто- z рого в точке (о,о,-^-). Будем рассматривать сум- марное поле рассеяния в случае падения на указанную пару рассеивателей плоской волны E0i exp(ikix) , распространяющейся для определенности в сторону возрастания величины z , т. е. снизу вверх. Поле ищется суммированием многократно рассеянных плоских волн (принцип суперпозиции уместен, т. к. каждой падающей плоской волне соответствует своя совокупность рассеянных волн, которые вместе с падающей обеспечивают выполнение граничных условий на рассеивателе, и так для всех пар (падающая плоская вол-на—соответствующие ей рассеянные волны)). Отметим, кроме того, что построенное таким образом решение является единственным в силу единственности составляющих его слагаемых, начиная с первичных полей рассеяния, что определяется выбором соответствующих условий излучения Сильвера—Мюллера (а следовательно, и Зоммер-фельда).

Пусть результирующее поле каждого рассеивателя после всех переотражений определяется выражением (17), где под x ₀ понимаются координаты центра соответствующего рассеивателя. Обозначим в (17) результирующие спектры векторов поляризации (рсвп) ¹ T _m ⁿ ( k _i, k _s) и ² T _m ⁿ ( k _i, k _s) соответственно. Рассмотрим, например, процесс формирования рсвп S ₁ в верхней полусфере, т. е. ¹ T ₁¹( k _i , k _s) . Происходит следующее. Плоская волна E _0i exp( i k _i x ) , распространившись мимо рассеивателей S ₁ и S ₂ , вызовет на них первичные поля рассеяния соответственно со спектрами векторов поляризации (свп)

1 A 1 n ( k i , k s ) E 0i exP ^{( -} i ^a i 4 ° ) и

2Ain(ki,ks)Eoi exp(iai 40), которые и окажут влияние на формирование интересующей нас рсвп 1 T11(ki,ks) (множители exp(±iai Z°) отвечают фазе падающей плоской волны соответственно на S2 и S1 ). Поясним это на примере первичного рассеянного поля с свп 1 A11(ki,ks)E0i exp(-iai Z°). Это поле, порожденное плоской волной на S1 , распространяется вверх, достигает S2 , переотражается от него, идет далее вниз, переотражается от S1 , порождая первую добавку к рсвп, снова идет вверх и т. д. до бесконечности. В итоге формируется составляю- щая 11T11(ki,ks) рсвп 1 T11 (k i , k s ) , обусловленная первичным рассеянным полем на S1 с свп 1 A11(ki,ks)E0i exp(-iai 4°). Аналогично формируется составляющая 12T11(ki,ks) рсвп 1 T11(ki,ks), вызванная первичным рассеянным на S2 полем с свп 2 A12 (k i, k s) E 0i exp(iai Z°): первичное поле 2A12(ki,ks)E0i exp(iai -20-) на S2 распространится вниз, переотразится от S1 , вызвав свою первую добавку к 12T11(ki ,ks) , затем пойдет вверх, снова переотразится от S2 и т.д. до бесконечности. Таким образом, необходимо вычислить сумму

• ¹    T/ ( k i , k s ) = 1 T ¹( k i , k s ) + 2 T i1 ( k i , k s ). (30)

Используя выражение (16) для расчетов вторичных свп и действуя совершенно идентично тому, как это проделывалось для скалярного случая [16] или когда роль второго рассеивателя играла граница раздела [17], получим следующие ставления

¹ 1 T 1 ¹( k i , k s )

exp( - ia i z ₀ /2)

= £ ( A¹ ) n [ 1 A E 01 ] ( k i , k s ) = n = 0

= (l - A11 )—1 [1 AEoi ](ki,ks), пред-

• 2    T/( k i , k s ) =

= :£(A11)n [1 T11 ](k i, k s) = n=0

= ( l - A 1 ¹ )^- 1 [ 1 T 1 ¹ ] ( k i , k s ),                (32)

где ¹ T ^ˆ ₁¹( k _i, k _s) определяется выражением

• ¹    T 11 ( k i , k s ) =

zi

= exp( ia i —) — x 2 2n

[¹ A 2 ¹( k n , k s )][² A 1 ²( k i , k n ) E 0i ]

------------------------x xj

R ²

an x exp(ianzo)dknxdkny ,

а оператор A ₁¹ определяется следующим образом:

^ 1 ¹[ T ]( R i , k s ) =

( i ) 2Г1 A 21 ( k m , k s ) f _f ² A i ²( k n , k m ) T ( k i , k n ) I

V ^П J R 2 ^a m V R 2           ^a n

exP ^{( i a} n z 0^)d k nx ^d k ny

X exp ⁽ i«_mZ 0^)d k mx d k my .

Как видно из (34), оператор A ₁¹ вычисляет добавку к рсвп ¹ T ₁¹( k _i, k _s) за один цикл: рассеянная на S ₁ волна достигает S ₂ , переотражается обратно, достигает S ₁ и вызывает очередное приращение рсвп ¹ T ₁¹ ( k _i , k _s ) . Заметим, что учет конечного числа членов рядов (31), (32) может быть использовано для приближенного вычисления составляющих рсвп.

Формально ряды Неймана (31), (32) сходятся, когда норма оператора (34) меньше единицы. Однако из физических соображений ясно, что если соответствующие рсвп существуют, то по построению единственного решения представляют собой именно ряды типа (31), (32), т. к. эти ряды лишь отражают физику происходящих процессов и представляют собой решение, альтернативное описанному в работах [ 1-15 ] .

Для сходящихся рядов (31), (32) можно обратить оператор ( l - A 1 ¹ ) стандартным образом, после чего получаем интегральные уравнения для определения составляющих рсвп ¹ T ₁¹( k _i , k _s) :

( l — 41 ^T ] ( k i , k s ) =

= 1 A 1 ^{1 ( k} i , ^k s^{) E} 0i exP ⁽ - ^{i a} i y).           (35)

( l - 41 )[ 2 T 1¹ ] ( k i , k s ) = 1 T/ ( k i , k s ),        (36)

где оператор A ₁¹ определяется из (34).

Отметим, что после определения величины рсвп ¹ T ₁¹( k _i, k _s) рассеивателя S ₁, легко получить рсвп ² T ₁¹( k _i, k _s) рассеивателя S ₂ . Для этого, как легко заметить, к первичной составляющей ² A 11 ( k i , k _s) E _0i exp( ia i “ у), вызванной падением плоской первичной волны, необходимо добавить составляющую, вызванную рассеянием на S ₂ суммарного поля рассеяния рассеивателя S ₁ с рсвп ¹ T ₁¹ ( k _i , k _s ) . Или в окончательном виде

² T 11 ( k i , k s ) = ² A /( k i , k s ) E oi exp( ia i Z ⁰) +

i     ² A 1 ¹( k n , k s )¹ T 1 ¹( k i , k n )

+X

^{2 П} R 2            ^a n

^X exp ^{( i a} n z o^)d k nx d k ny .                     ⁽³⁷⁾

Поступая совершенно аналогично, найдем соответствующие интегральные уравнения для ²₁ T ₁²( k _i, k _s) и ²₂ T ₁²( k _i, k _s) , являющихся составляющими рсвп ² T ₁²( k _i, k _s) рассеивателя S ₂ в нижнем полупространстве:

2 T12(k i, k s)=21T12(k i, k s)+^(k i, ks),(38)

( l - A 22 )[ ² 1 T 1 ² ] ( k i , k s ) =

=2A12(ki, ks)E0i exp(iai Z0),(39)

(i - A22 )[22T12 ](ki,ks)=2T12(ki,ks),(40)

где ² T ^ˆ ₁² ( k _i, k _s) определяется выражением

2 T12(k i, ks) = zi

= exp( - ia _i⁰) X

2 2 n

Xj

R ²

[² A 1 ²( k n , k s )][ 1 A 11 ( k i , k n ) E 0i ] _X

a n

^X exp ^{( i a} n z o^)d k nx ^d k ny ,

а оператор A ₂²[ T ]( k _i, k _s) равен:

A 2 ²[ T ]( k i , k s ) =

(

Xj

^V R ²

² A 1 ²( k m , k s )

X

^T J R 2      ^a m

¹ A 2 ¹( k n , k m ) T ( k i , k n )

^a n

^ ^e xp ^{( i a} n z 0^{)d k} nx d k ny

J

X

^{X e}xp^{( i a} m z 0 ^{)d k}mx d k my .

Рсвп рассеивателя S ₁ в нижнем полупространстве определяется из выражения

1 T i ²( k i , k s ) =

=1 A12(ki, ks)Eoi exP(-iai zO) + i     1A12 (kn ,ks)2 T12(ki,kn)

+                                 X

^{2 n} R 2            ^a n

X exp ⁽ KZ^ o^)d k nx d k ny .             ⁽⁴²⁾

Пусть теперь первичная волна распространяется сверху вниз. Тогда останутся верными все выражения (30–42), если в них произвести следующие изменения. Первичные свп будут соответственно

¹ An ( k i , k s ) E 0i exp( i a i z⁰-)    и

• ²    A 2 n ( k i , k s ) E oi exp( - i a i z 2).

Далее в выражениях (30–42) во всех функциях свп, содержащих аргумент k _i , необходимо правый нижний индекс в обозначении функции и аффинора поменять с 1 на 2, а во всех экспонентах, содержащих a i , поменять знак на противоположный. Все остальные обозначения и выражения останутся без изменений. Например, выражения (39), (40) примут соответственно вид

( l - A 22 ) [ 21 T 2 ² ] ( k i , k s ) =

= ² A 22 ^{( k} i , k s ^{) E} 01 exP ⁽ — ^{i a} i ^ Z ⁰) ,

( l — A 22 )[ 22 T 2 ² ] ( k i , k s ) = 2 T 22 ( k i , k s ).

Таким образом, получены все выра ж ения для определения рсвп двух рассеивателей ¹ T _m ⁿ ( k _i, k _s) и ² T mⁿ ( k i , k _s), m , n = 1,2 . Такая информация является, безусловно, полезной хотя бы для того, чтобы судить о степени возмущения исходных свп ¹ A mⁿ ( k i , k s ) E 0i и ² A mⁿ ( k i , k s ) E 0i .

ОБОБЩЕНИЕ НА ПРОИЗВОЛЬНОЕ ЧИСЛО РАССЕИВАТЕЛЕЙ И ПРОИЗВОЛЬНОЕ

ПЕРВИЧНОЕ ПОЛЕ

В тех случаях, когда возмущением свп пренебречь нельзя, практически более значимой является, по-видимому, информация о совокупной свп системы, состоящей из рассматриваемых двух рассеивателей. Последнюю легко получить, пользуясь выражением (17) и принципом суперпозиции. Окончательно имеем для совокупной свп T mⁿ ( k i , k s ):

T> i , k s ) =

= ¹ T 1 ( k i , k s )exp( ia s Z 0 ) +

+ 2 Tm(k i, k s)exp(-ias yX Tm2(k i, k s) = m = 1,2 .

= ¹ T m 2 ( k i , k s )exp( - ia s Z 0 ) + + ² T m 2 ( k i , k s )exp( ia s Z 0 )

После вычисления свп уже можно проделать три важные вещи.

Во-первых, вычислить результирующую мр. В скалярном случае рассматриваемой задачи [16] вычисление скалярного спектра, аналогичного свп (43), уже означало вычисление совокупной амплитуды рассеяния, аналогичной мр для двух тел при падающей плоской волне единичной амплитуды и нулевой фазы. В векторном случае это не так. Анализ показывает, что в этом случае необходимо для определения четырех элементов результирующей мр дважды находить свп (43): отдельно для падающих плоских волн единичной амплитуды и нулевой фазы, поляризованных по hi и vˆ i векторам соответственно. Тогда элементы резуль- n тирующей мр T m (k i, k s) = nn

T m ,_и T m ,12

г ⁿ t"

^ T m ,21 ^T m ,22

равны

n n   n n

T m,11 = hihs T m (ki,ks), T m,21 = hivs T m (ki,ks), nn  nn

T ^m ,12 = v i h s ^T m ^{( k} i , ^k s ), ^{T m} ,22 = v i v s ^{T m ( k} i , ^k s ),

где, например, h _i v _s T ⁿm ( k _i, k _s) означает v ˆ_s -составляющую свп (43), вычисленную при падении h _i -поляризованной плоской волны единичной амплитуды и нулевой фазы, и т.д. Как показывает (17), центр совокупного рассеивателя, состоящего из описанных двух рассеивателей, находится посредине между центрами обоих рассеивателей, т. е. в данном случае в начале координат.

Во-вторых, умение вычислять результирую- щую мр Tm(ki ,ks) системы, состоящей из двух рассеивателей, позволяет последовательно решить задачу о N рассеивателях. А именно: сначала рассматривается система из двух рассеивателей, находится их результирующая мр, и оба рассеивателя заменяются одним, фиктивным, который обладает их результирующей мр с центром, лежа- щим посредине между центрами исходных рассеивателей. Затем рассматривается система рассеивателей, состоящая из третьего рассеивателя и описанного фиктивного, находится их результирующая мр и т.д., пока не будут исчерпаны все рассеиватели и не найдена единая результирующая мр всех N рассеивателей. Правомерность описанной итерационной процедуры следует из принципа суперпозиции.

В-третьих, после вычисления результирующей мр необходимого числа рассеивателей можно вычислить результирующий свп (16) всей системы рассеивателей при облучении системы рассеивателей направленным источником с полем (15). В (16) теперь уже будет фигурировать аффинор, ассоциированный с результирующей мр. Само поле рассеяния можно вычислить из выражения (17). При этом очевидно, что центр системы рассеивателей находится в их геометрическом центре.

МНОЖЕСТВЕННОЕ РАССЕЯНИЕ В СИСТЕМЕ: (ПЛОСКАЯ ГРАНИЦА РАЗДЕЛА— РАССЕИВАТЕЛЬ)

Представляет интерес получить из вышеприведенных выражений для системы двух рассеивателей результаты для случая, когда одним из рассеивателей является отражающая плоскость (плоская граница раздела). Для этого вначале найдем матрицу рассеяния границы раздела.

Пусть плоскость z = 0 служит границей раздела однородного верхнего полупространства z >  0 и нижнего слоисто-неоднородного полупространства z <  0 (идеальные границы являются частным случаем этой модели). При падении плоской волны ^E oi exp ⁽ i ⁽ k ix x + к у у - a l z )) из верхнего полупространства на границу раздела в нем образуется отраженная от границы плоская волна E _s exp( i ( k_lxx + k ly y + a l z )), где E _s — вектор поляризации отраженной волны. Для вычисления мр отражающей плоскости формально воспользуемся выражением (13). В этом случае имеем

^E 5 exP ⁽ i ^{( k}ix x ^{+ к}у У ^{+ a} i z )) =

= —V_n i ( a s ) a s S ( k i x - k sx ) S ( k i у - k s у ), i                                            (46)

• n , l = 1,2.

Здесь использовано фильтрующее свойство δ -функций. Функции V_nl (a i ) = V_nl (a _s) имеют смысл соответствующих коэффициентов отражения для волн различной поляризации, рассмотренных во многих работах, например в [ 27 ] . Действительно, пусть единичный вектор падающей плоской волны горизонтально поляризован, тогда формально вектор E _s из (45) равен:

E s = E _H( a i ) h s + V 2i ( a i ) v_s.              (47)

В случае вертикальной поляризации имеем

E s = V ,2 ( a i ) h s + V 22 ( a i )v_s.              (48)

Впрочем, в случае плоскослоистой среды из физических соображений следует, что недиагональные члены мр должны быть равны нулю V ₁₂ = V 21 = 0 и мр — диагональная.

Перейдем к постановке задачи. Пусть центр рассеивателя S ₂ по-прежнему находится в точке ^z

(0,0, 20 ) , рассеиватель S1 отсутствует, однако присутствует граница раздела z = -z0 /2 с элементами мр вида (46). Первичное поле имеет вид E 01 exp( i ( k ixx + k 1уу - ai z)). Найдем поле рассеяния выше и ниже рассеивателя. Для этого в выражениях (30–42) во всех функциях свп, содержащих аргумент ki необходимо правый нижний индекс в обозначении функции и аффинора поменять с 1 на 2, а во всех экспонентах, содержащих ai, поменять знак на противоположный. Все остальные обозначения и выражения останутся без изменений. Роль S1 , разумеется, играет отражающая плоскость. С учетом этих замечаний и выражения (46) выпишем выражения для операторов (34) и (41). Для оператора A11 имеем i f A> i, k s)E oi x

2n j     as x exp(i(ksxx + ksуУ + asz))dksxdksу .

A l [ T ]( k i , k s ) =

i

= — exp( ia s z 0 ) x

2 n

Анализ последнего выражения показывает, что элементы мр отражающей плоскости равны:

Tnl ,2 ( k l , k s ) =

= '^V ( aa ( k i x - k s x ) S ( k _t у - k s у ) =

xj

R ²

(¹ a 2 ¹( k s ))² A 1 ²( k n , k s ) T ( k i , k n )

x

an x exp(ianz0)dk„xdk„y ,

где ¹ a ₂¹( k _s) — аффинор, равный

• 1    a> s) = hs Vn(as)h s + Vs V„(as)Vs.(50)

Для оператора A ₂² имеем

A 2 [ T ]( k i , k s ) =

= f ² A 1 ²( k m , k s V a 2 ( k m ) T ( k i , k m ) _x

2П R2

X exP(i2amz0)dkmxdkmy ,(51)

где ¹ a ₂ 1 ( k m ) также определяется из (50) при k = = ^k m .

Теперь для определения свп поля рассеяния ниже рассеивателя S ₂ необходимо воспользоваться видоизмененными интегральными уравнениями (39), (40):

( l - A 2 ) [ 21 T 22 ] ( k i , k s ) =

= ² A ²( k i , k s ) E 0i exp( ia i z ⁰),

(l - A 2 )[22 T22 ](k i, k s) = 2 T22(k i, k s), где

• ²    T> i , k s ) =

= [² A ² ( k i , k s )][ 1 a 2 ( k i ) E 0i ] exp( ia i 32), а также (35), (36)

( l — A i ¹ ’I T' ] ( k i , k s ) =

= A 2 ^{1 ( k} i , ^k s^{) E} 0i ^e xp ^{( - i a} i y),              (52)

( l - A )[ 2 T 2 ¹ ] ( k i , k s ) = 1 T ₂ * ( k i , k s ),        (53)

где

• ^{1    r}T 2 ¹( k i , k s ) =

= [ 1 a 2 ¹ ( k s )][² A ² ( k i , k s ) E 0i ] exp( ia i z ⁰).

Кроме того, необходимо видоизменить выражение (37), а именно

• ²    T 21 ( k i , k s ) = ² A 2 ¹ ( k i , k s ) E 0i exp( ia i z ⁰) +

i     ² A 1 ¹( k n , k s )¹ T 2 ¹( k i , k n )

+x

2 ⁿ R 2          a

• ^x exp ^{( i a} n z 0^)d k nx d k ny .

Эти выражения позволяют вычислить рсвп ¹ T 2 ¹( k i , k s ), ² T 2 ¹( k i , k s ) и ² T 2 ²( k i , k s ). Однако в данном случае объединять рассеиватели в виде совокупной свп (43) нецелесообразно, а следует представить поле рассеяния в виде полей реального и мнимого рассеивателей. Центр мнимого рассеивателя, очевидно, находится в зеркальной от-3

носительно границы точке (0,0, - —z ₀). Воспользовавшись выражением (17), получаем для поля рассеивателя

Es = —J s   2n 12

^{1 T} 21^{( k} i , ^k s^)ex P ⁽ ia s z 0^/2)

+

• ² T2 ( k i , k s )exp( - ia s z 0 /2) +

a

X exp(i(ksxx + ksуУ + as z))dksxdksy выше рассеивателя и

E s

=f

2 n J,

R

¹ T 2 ^{1 (} k i , k s^)e xp ⁽ ia s z 0^/2)

x as

X exp(i(ksxx + ksуУ + asz))dksxdksу + f T2 (k i, ks)exp(ias z0/2) +X

1 2                ^a s

^{X e} xp ⁽ i ⁽ k s x x ⁺ k s у У ^{+ a} s ^{z ))d} k s x ^d k s у

ниже рассеивателя.

После этого выделятся составляющие поля реального и мнимого рассеивателя, как в скалярном случае [17]. Кроме того, использование выражений (18–20) позволяет получить геометрооптическое представление поля рассеяния реального и мнимого рассеивателей.

ГЕОМЕТРООПТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЕШЕНИЯ ЗАДАЧИ МНОЖЕСТВЕННОГО

РАССЕЯНИЯ

Рассмотрим далее случай, когда в поле первичной волны, образованной некоторым излучателем, по-прежнему находятся два рассеивателя. При этом ограничимся ситуацией, когда можно принять допущение, что рассеиватели находятся друг по отношению к другу и к излучателю в зоне Фраунгофера. Тогда можно воспользоваться выражениями (25), (29) для расчета свп рассеивателей и далее вычислить результирующие свп рассеивателей. Выражения (25), (29) при фиксированных расстояниях между объектами имеют порядок точности O(к -2), т. е. точность этих приближений растет с частотой.

Как всегда, отклик вначале будем искать на воздействие первичной плоской волны. Рассеяние при произвольной падающей волне может быть найдено по вышеописанной методике. Пусть плоская первичная волна E _0i exp( i k _i x ), идущая для определенности снизу вверх, вызовет на рассеивателях S 1 и S ₂ два невозмущенных рассеянных поля с свп соответственно

¹ A '^{( 6} i , Ф i , 6 1s , Ф s ) E 0i ^ex P ⁽ - i ^a i у) и

² A '^{( 6} i , Ф i , ⁶ 2s , Ф s ) E 01 ^ex P ^{( i a} i y)

(свп представлены в сферических координатах; 6 _1s, ф_s,6 _2s, ф _s — сферические углы относительно центров). Как показано выше, каждое из этих первичных рассеянных полей будет принимать участие в формировании результирующих рассеянных полей обоих рассеивателей. Получим приближение, например, для рсвп ¹ T '( 6 _i, ф _i, 6_1s, ф _s),

6 1s е [0,-]:

• ¹    T '( 6 i , ф i , 6 1s , Ф s ) =

= 1 T '( 6 i , Ф i , 6 1s , Ф s ) + 2 T '( 6 i , Ф i , 6 1s , Ф s ).

Как нетрудно увидеть, вычисление последней рсвп распадается в этом случае на вычисление двух геометрических прогрессий:

mT'(6i,Фi,61s,Фs) ^(q)la0m , m = 1,2, l=0

где a01 =1 A'(6i,Фi,61s,Фs)E0i exp(-iai Z°);(58)

a 02 = P A '(61i = П 61s, Фs)]x x2A'E0iexp(iai z0) exp^ikzo);(59)

q =

^{2 e} xp ⁽ ikz 0 ) ) ²

V

x

^z 0

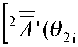
[ 1 A '( 6 _H = п , 6 1s , Ф s ) ] x 0, 6 2s = п ) ] .

Здесь q — аффинор, ассоциированный с матрицей, равной произведению матриц, ассоциированных с аффинорами ¹ A ' и ² A ' из (60) (произведение осуществляется в том же порядке, что и в (60)); в (59-60) учтено также, что при 6 = 0 или 6 = п зависимость от ф пропадает.

Полагая справедливым условие ||T=||< 1, где Г= — матрица, ассоциированная с аффинором q , q получим для рсвп

¹ T '( 6 i , ф i , 6 1s , ф s ) = Q ' ( a 01 + a 02 ) , 6 1s е [0, П -].

Здесь Q ' — аффинор, ассоциированный с матрицей ( I - T q ) ^{- 1}, где I — единичная матрица. Равенство (61) следует из того факта, что ряду (57) соответствует матричный операторный ряд

Y = 2 TqX • где X , Y — вектор-столбцы. Тогда имеем

Y = ( I - T ₌) ^{- 1} X .

q

Учитывая, что

X ' = (( a 01 + a 02 ) h , ,( a 01 + a 02 ) v/ ), Y ' =( * T h s , * T . ), имеем (61) (штрих означает здесь транспонирование).

П

Используя (37), получаем для 6 _2s е [0,— ]

• ²    T '( 6 1 , ф i , 6 2s , ф s ) =

= ² A ' ( ⁶ 1 , Ф i , ⁶ 2s , Ф s ) E 0i exp( i ^a i Z ° ) +

+ ^x^ [ 2 A '( 6 i = 0, 6 „, ф . )] x z ₀

x [ * T '( 6 i , Ф i , 6 1s = 0)].                         ⁽⁶²⁾

В выражениях (61), (62) фs е [0,2п]. Аналогично находятся результирующие свп в оставшейся п области определения 6s е [—, п], фs е [0,2п].

А именно:

• ²    T '( 6 1 , Ф 1 ,6 2s , Ф s ) = P '(а 01 + a 02 ),         (63)

  
  

  ¹ T '( 6 1 , ф i , 6 1s , Ф s ) =

  
  

= 1 A '^{( 6} i , ф i , ⁶ 1s , ф s^{) E} 0i exp ^{( -} i ^a i 4 ° ) +

+ ^p z ) [ 1 1че,,= п, 6 „, ф s )] X z ₀

X[2 T'(6 i, ф i,6 2s = П )], где a 01 = 2A ' (6i , Фi , 62s , фs ) exP(iai ^ ;

~ 02 =^{[ 2} A '^{( 6} 1i = 0, ⁶ 2s , Ф s^{) ] x}

x["A '(6,, ф,, 6„ = 0)]x x E 0i exp(-ia i z0)exP*ikz0>;

P'— аффинор, ассоциированный с матрицей (I - Tp)-1. Матрица T= ассоциирована с аффино- ром p , равным:

p =

Г e^ ) ²

I z o J

[² A '( 6 2i = 0, 6 2s , ф s )] X

X [ 1 A '( 6 ii = П , 6 s = 0)].

Выражения для случая, когда плоская первичная волна набегает на рассеиватели сверху вниз получаются из (58–67), если во всех экспонентах, содержащих a i , поменять знак на противоположный. Отметим, что при условии R _s >>  z ₀ ( R _s, 6 _s, ф _s— сферические координаты точки наблюдения относительно центра системы рассеивателей), в выражениях (58–67) можно положить 6 1s = 6 2s = 6 s .

Выражение для совокупной свп двух рассеивателей в геометрооптическом случае может быть получено из выражения (43), выписанного в сферической системе координат по отношению к началу координат (т.е. к средине отрезка, соединяющего центры рассеивателей):

T '( 6 i , ф i , 6 s , ф s ) =

= 1 T '( 6 i , ф i , 6 s , ф s )exp( ik cos( 6 s ) z ^) +

+ ² T ' ( 6 i , ф i , 6 s , ф s ) exp( - ik cos( 6 s ) z ^).         (68)

Аналогичный результат может быть получен стандартной процедурой перехода к предельным расстояниям. Пусть R— радиус-вектор точки на- блюдения относительно начала координат, а Rm— радиус-векторы, соединяющие центры рассеивателей с точкой наблюдения (m = 1,2); rm — радиус-векторы центров рассеивателей относительно начала координат. Тогда при R, Rm ^^ ( R = |R| , Rm = |R m| ) имеем usm- = (m T' (6i, фi, 6s, Фs) exp(-ikRrm ))x exp(ikR)                            (69)

X p); m = 1,2, R где u sm^ — предельное поле m -го рассеивателя;

R

R = R — единичный вектор в направлении от начала координат к точке наблюдения. Суммируя поля (69) и выделяя предэкспоненту, снова придем к выражению (68) для совокупной свп двух рассматриваемых рассеивателей.

Далее может быть применена процедура вычисления совокупной свп системы произвольного числа рассеивателей, описанная выше.