Метод решения задачи о движении нагрузки по ледяному покрову водоема по сложной траектории
Автор: Галабурдин А.В.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 1 т.23, 2023 года.
Бесплатный доступ
Введение. Освоение полярных районов Мирового океана способствовало повышению интереса к изучению волновых процессов в водоемах с ледяным покровом, обусловленных действием подвижной нагрузки. В большинстве работ отечественных и зарубежных ученых ледяной покров рассматривался как упругая или вязкоупругая пластина, нагруженная прямолинейно движущейся вертикальной силой. Однако при моделировании воздействия транспортных средств на ледяной покров представляет интерес рассмотрение задач, в которых сила движется по более сложной траектории. Поэтому целью данного исследования является разработка метода исследования поведения ледяного покрова под действием силы, движущейся по траектории сложной формы, подчиняясь произвольному закону движения.Материалы и методы. Предложен метод решения задач о действии движущейся произвольным образом силы по ледяному покрову водоема конечной глубины, заполненного невязкой несжимаемой жидкостью. Ледяной покров рассматривался как вязкоупругая пластина, лежащая на поверхности жидкости, находящейся в состоянии потенциального течения. На верхнюю поверхность пластины приложена сосредоточенная сила, движущаяся по произвольной замкнутой траектории и являющаяся периодической по времени. На нижнюю поверхность пластины со стороны жидкости действует гидродинамическое давление. В силу периодичности приложенной к пластине нагрузки при решении дифференциальных уравнений, описывающих поведение данной системы, использовали интегральное преобразование по времени. Далее, применяя традиционные методы, получили формулы для вычисления напряжений и перемещений в пластине и компонент вектора скорости частиц жидкости. Эти формулы представили в виде повторного интеграла. Для вычисления интегралов использовали численные методы.Результаты исследования. Расчеты показали, что прогиб ледяного покрова заметно увеличивается с ростом скорости и касательного ускорения движения нагрузки. К росту прогиба также приводят увеличение времени релаксации льда и уменьшение радиуса траектории движения нагрузки. Рассчитано распределение вектора скорости частиц жидкости по глубине водоема.Обсуждение и заключения. Предложенный метод показал свою эффективность при решении задач о действии подвижной нагрузки на ледяной покров водоема. С его помощью исследовано влияние на прогиб ледяного покрова кривизны траектории движения и механических свойств льда, кинематических характеристик движения нагрузки. Метод моделирует воздействие транспортных средств на ледяной покров водоема. Результаты его применения могут быть использованы при строительстве ледовых дорог или аэродромов на льду.
Бесконечный ледяной покров, движущаяся нагрузка, произвольная замкнутая траектория, переменная скорость
Короткий адрес: https://sciup.org/142237664
IDR: 142237664 | УДК: 539.3 | DOI: 10.23947/2687-1653-2023-23-1-34-40
Текст научной статьи Метод решения задачи о движении нагрузки по ледяному покрову водоема по сложной траектории
Original article
Method for Solving the Problem of Load Movement over the Ice Cover of a Reservoir along a Complex Trajectory
Alexander V Galaburdin
Don State Technical University, 1, Gagarin sq., Rostov-on-Don, Russian Federation
Introduction. The development of the polar regions of the World Ocean contributed to an increased interest in studying wave processes in water bodies with ice cover caused by the action of a mobile load. In most papers of domestic and foreign scientists, the ice sheet was considered as an elastic or viscoelastic plate loaded with a rectilinearly moving vertical force. However, when modeling the impact of vehicles on the ice cover, it is of interest to investigate problems in which the force moves along a more complex trajectory. Therefore, this study aims at developing a method for studying the behavior of the ice cover under the action of a force moving along a trajectory of a complex shape, obeying an arbitrary law of motion.
Materials and Methods. A method for solving problems of the action of an arbitrarily moving force on the ice cover of a reservoir of finite depth filled with an inviscid incompressible fluid is proposed. The ice cover was considered as a viscoelastic plate lying on the surface of a liquid in a state of potential flow. A concentrated force moving along an arbitrary closed trajectory and being periodic in time was applied to the upper surface of the plate. Hydrodynamic pressure acted on the lower surface of the plate from the liquid side. Due to the periodicity of the load applied to the plate, an integral time transformation was used to solve differential equations describing the behavior of this system. Further, using traditional methods, formulas were obtained for calculating stresses and displacements in the plate and components of the velocity vector of liquid particles. These formulas were presented in the form of an iterated integral. Numerical methods were used to calculate integrals.
Results. Calculations showed that the deflection of the ice cover increased markedly with the growth of speed and tangential acceleration of the load movement. An increase in the relaxation time of ice and a decrease in the radius of the trajectory of the load also caused an increase in deflection. The distribution of the fluid particle velocity vector over the depth of the reservoir was calculated.
Discussion and Conclusions. The proposed method has shown its efficiency in solving problems about the impact of a moving load on the ice cover of a reservoir. With its help, the influence of the curvature of the trajectory of motion and the mechanical properties of ice, the kinematic characteristics of the movement of the load on the deflection of the ice cover was investigated. The method simulates the impact of vehicles on the ice cover of a reservoir. The results of its application can be used under the construction of ice roads or airdromes on ice.
Введение. В последнее время, в связи с освоением северных территорий и районов Мирового океана, огромное внимание уделяется проблемам изучения поведения ледяного покрова под действием внешней нагрузки. Этим вопросам посвящено большое количество работ отечественных и зарубежных ученых. Воздействие на вязкоупругую плавающую пластину импульсной движущейся нагрузки рассматривалось в [1]. Воздействие подвижной нагрузки на ледяной покров, примороженный к стенкам канала, представлено в [2, 3]. Колебания ледяного покрова, обусловленные движущейся с постоянной скоростью нагрузкой, рассматривались в [4]. Поведение полубесконечного ледяного покрова при действии на него равномерно движущейся нагрузки изучалось в [5]. Распространения волн, возбуждаемых вдоль канала с ледяным покровом, рассмотрены в работе [6]. В [7] при моделировании применялись нелинейные модели. В монографии [8] приведены результаты исследований поверхностных волн в море с плавающим битым и сплошным ледяным покровом. Разрушение льда под действием движущейся нагрузки рассматривалось в [9]. В приведенных выше работах в основном рассматривалось прямолинейное движение нагрузки. Целью данного исследования являлась разработка метода решения задачи о воздействии силы, движущейся по ледяному покрову произвольным образом. Достижение
Механика
поставленной цели позволяет более точно моделировать воздействие на ледяной покров транспортных средств, движение которых происходит часто по достаточно сложным траекториям и по сложному закону.
Постановка задачи. Рассматриваются колебания бесконечного ледяного покрова, лежащего на поверхности водоема конечной глубины, под действием силы, движущейся произвольно по замкнутой траектории. Ледяной покров моделируется тонкой вязкоупругой пластиной, механические свойства которой описываются моделью Кельвина-Фойгта. Водоем наполнен несжимаемой жидкостью.
Материалы и методы. Изгиб ледяного покрова описывается дифференциальным уравнением [7]:
где W(x,y,t) — прогиб ледяного покрова; D=Eh3/(12( 1–μ2 )); Е — модуль Юнга; μ — коэффициент Пуассона; h — толщина ледяного покрова; τ o — время релаксации деформаций; ∆2 =∂ x 4+2∂ x 2 ∂ y 2+∂ y 4 ; ρ л — плотность льда; ρ в — плотность воды; с-2 = ρ л h/D, k= ρ в g/D, b= ρ в /D; P(x,y,t) — действующая на поверхности льда нагрузка; Ф (x,y,z,t) — потенциал движения жидкости. Поведение жидкости подчинено уравнению:
∆Ф=0.
Граничные условия на границе лед-вода при z =0 и на дне водоема z=–H ( H — глубина водоема) имели вид: ∂ t W=∂ z Ф | z=0 , ∂ z Ф | z=-H =0.
Предполагалось, что сила P (x, y, t) перемещается по произвольной замкнутой траектории γ произвольным образом. При этом полагалось, что P=P(s(t)), где s — дуговая координата, отсчитываемая от некоторой фиксированной точки кривой γ. Если функция s(t) является периодической с периодом T, то вполне очевидно, что периодической будет и величина P(s(t)), причем также с периодом T. Параметрическое задание траектории принималось в виде:
где t — время.
Рассматривая установившийся процесс и применяя интегральное преобразование по переменным x и y , а также конечное интегральное преобразование по t на интервале [ 0; T ], получим:
(1– i ω n τ o ) p 4 W 0 – с- 2ω n 2 W 0 + kW 0 + bi ω k Ф 0 | z=0 = P 0 /D ,
∂z Ф0 – p Ф0=0, где W0, Ф0 — изображения неизвестных функций W и Ф, p2=λ2+ α2; λ; α — параметры интегральных преобразований, соответственно, по переменным x и y; ωn=2πn/T, n=0, 1, 2, 3, … . Решая второе уравнение с учетом граничных условий, получим:
Ф0 =-i ω nW0ch(p(z+H))/psh(pH).
Тогда из первого уравнения следует:
W 0 =P 0 /((c-2+bcth(pH)/p) ω n 2-p4-k+i ω n τ o p4).
Движущаяся сосредоточенная сила аппроксимировалась функцией:
P(x,y,t)=ε2exp(–ε2((x–xo(t))2+(y–yo(t))2))/π, где ε — параметр.
Далее, выполняя вполне очевидные преобразования, можно получить:
T to
2nD JJ
p
to
n = 1
' r ln cos ( to n ( t - T ) )
r 2 n sin ( Ю n ( t - T )) ^
J o ( pR ) e - p 2 /4"
d τ dp
r in =(c2+bcth (pH)/p) to „-р4-к, r 2n = го n т o p4, R2= 5 2 + в 2 , δ =x o ( τ )–x, β = y o ( τ )–y.
Зная W , можно по известным соотношениям определить формулы для вычисления компонентов вектора перемещения и тензора напряжений в любой точке ледяного покрова.
При численной реализации предлагаемого метода возникает проблема, связанная с необходимостью вычисления интегралов, один из которых в качестве подынтегральной функции имеет сильно осциллирующую функцию при достаточно больших n , а второй является несобственным с бесконечным верхним пределом.
Для вычисления интегралов от сильно осциллирующих функций применялась квадратурная формула, полученная на основе использования метода кубических сплайнов [11]:
b N-1 'toxj+1 _ itoxj a to j=1 hj где hj — длины элементарных отрезков, на которые разбивается интервал [a; b]; S(x) — аппроксимация f(x)кубическим сплайном, Mj = 5 (Xj).
При вычислении несобственного интеграла использовалось приближенное соотношение J ” f(p)dp ~ - ^ f(p^)dp при достаточно большом A. Значение А выбиралось таким, чтобы оценка допускаемой ошибки Ц-^ f (p)dp| была достаточно малой.
Используя традиционные методы, можно получить необходимые оценки для вычисляемых величин. Например, для величины прогиба ледяного покрова данная оценка имеет вид:
X
Jw
A
( p ) dp < 4е
2 — A 2 /4е 2
W^ w(p)dp + J” w(p)dp.
При вычислении суммы ряда для ускорения его сходимости применялся метод сигма-множителей Ланцоша.
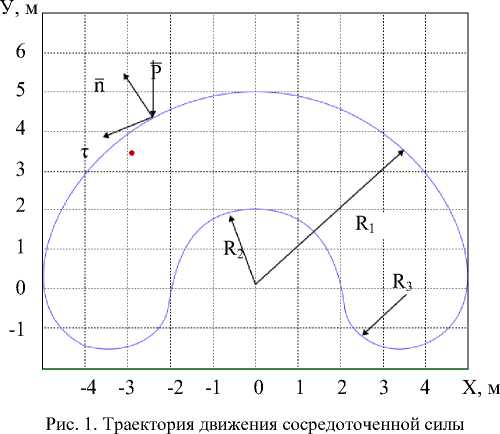
Результаты исследования. Расчеты проводились для случая действия единичной сосредоточенной силы, которая двигалась по замкнутой кривой, представленной на рис. 1:
—
s ( t ) =
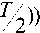
L • sin( a ( t
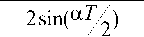
L
При этом полагалось, что толщина ледяного покрова h = 0,25 м , модуль Юнга материала пластины E= 500 000 000 H/м2 , коэффициент Пуассона μ = 1/3 , плотность льда ρ=900кг/м3, плотность воды ρ=1000 кг/м3, глубина водоема H =5 м, ε=2,5. Радиусы, определяющие форму траектории движения силы, принимались равными R1 =15 м , R2 =9 м , R3 =3 м (рис. 1).
На рис. 2 а приведено изменение прогиба ледяного покрова, а также максимальных значений нормальных напряжений (при z=±h) Sx и Sy (рис. б, в)
и при скорости движения единичной сосредоточенной силы v =7,4022 м/c и касательном ускорении wt=0.
W, м × 10
-5
-50
-6
Х, м
-50
а)
Sx, Н/м2
-200
У, м
-50
Х, м
-50
б)
Sy, Н/м2
У, м
-200
-50
Х, м
У, м
Рис. 2. Изменение прогиба и напряжений ледяного покрова: а — изменение прогиба; б — изменение напряжения Sx;
в — изменение напряжения Sy
На указанных графиках красной точкой обозначено место приложения силы, а синим цветом — траектория движения.
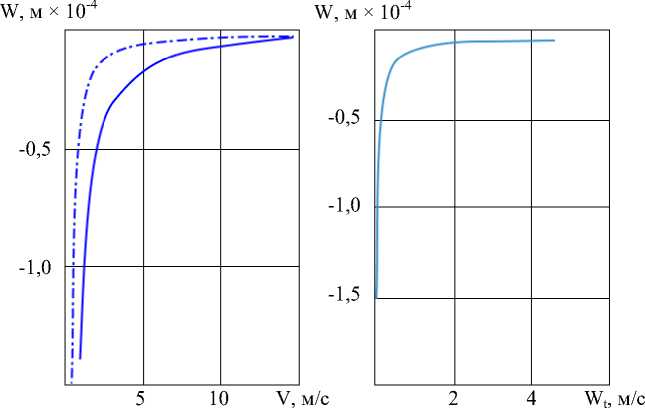
На рис. 3 представлена зависимость изменения максимального значения прогиба ледяного покрова от величины скорости движения силы ( а ) в момент t=T/2. Положение силы на траектории в данный момент отмечено красной точкой (рис. 1), при этом касательное ускорение w t =0. Приведено два графика, один из которых соответствует радиусу траектории R 1 =15 м (сплошная линия), а второй — радиусу R 1 =5 м (пунктирная линия). На графике б на рис. 3 изображена зависимость максимального значения прогиба ледяного покрова от величины касательного ускорения в момент t=T в точке траектории (2;0) на рис. 1 при скорости v=0. На графике на рис. 3 изображена зависимость максимального значения прогиба от величины времени релаксации деформации.
а) б)
-1,0
-1,2
-1,4
-1,6
-1,8
W, м×10-5
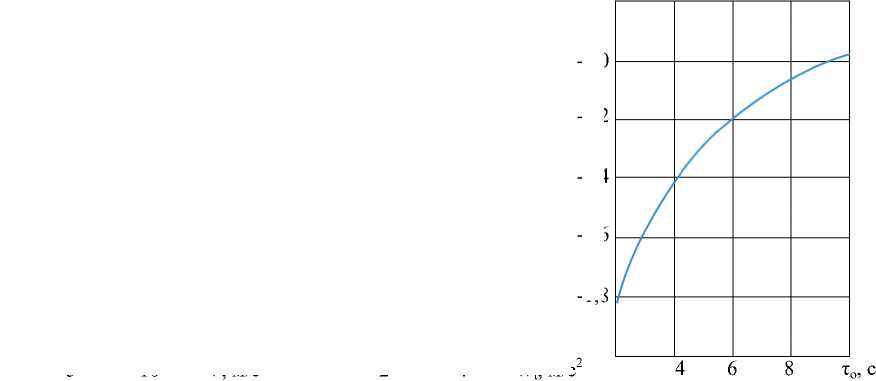
в)
Рис. 3. Зависимости прогиба ледяного покрова от: а — от скорости; б — касательного ускорения; в — времени релаксации
Поведение жидкости представлено на рис. 4, где изображено распределение вектора скоростей частиц жидкости по глубине водоема при t=T/2, скорости движения силы v=3,7011 м/c и ускорении wt=0.
Z, м
-5
-10
У, м
-50
20 0
X, м
Рис. 4. Распределение вектора скоростей частиц жидкости по глубине водоема
Обсуждение и заключения. Исследовано влияние кривизны траектории движения и механических свойств льда на прогиб ледяного покрова скорости и ускорения движения нагрузки. Расчеты показали, что прогиб ледяного покрова существенно зависит от скорости движения силы и ускорения движения.
Однако характер качественного изменения перемещений и напряжений в ледяном покрове, обусловленных действием движущейся силы при изменении скорости и ускорения движения, менялся слабо.
Заметное влияние на прогиб ледяного покрова оказывают механические свойства льда, в частности, время релаксации.
Полученные результаты и предложенный метод решения подобных задач могут быть использованы при строительстве ледовых дорог или аэродромов на льду. Кроме того, предложенный метод решения показал свою эффективность и может быть использован при решении других подобных задач.
Список литературы Метод решения задачи о движении нагрузки по ледяному покрову водоема по сложной траектории
- Wang K., Hosking R.J., Milinazzo F. Time-Dependent Response of a Floating Viscoelastic Plate to an Impulsively Started Moving Load. Journal of Fluid Mechanics. 2004;521:295-317.
- Shishmarev K., Khabakhpasheva T., Korobkin A. The Response of Ice Cover to a Load Moving along a Frozen Channel. Applied Ocean Research. 2016;59:313-326.
- Шишмарев К.А. Постановка задачи о вязкоупругих колебаниях ледовой пластины в канале в результате движения нагрузки. Известия Алтайского государственного университета. 2015;1-2:189-194.
- Козин В.М., Земляк В.Л., Кожаев А.В. Влияние физико-механических свойств льда на параметры резонансных изгибно-гравитационных волн. Ученые записки Комсомольского на Амуре государственного технического университета. 2019;1:36-45.
- Ткачева Л.А. Поведение полубесконечного ледяного покрова при равномерном движении нагрузки. Прикладная механика и техническая физика.2018;59(2):82-98.
- Korobkin A., Khabakhpasheva T., Papin A. Waves Propagating along a Channel with Ice Cover. European Journal of Mechanics - B/Fluids. 2014;47:166-175.
- Guyenne P., Pǎrǎu E.I. Computations of Fully Nonlinear Hydroelastic Solitary Waves on Deep Water. Journal of Fluid Mechanics. 2012;713:307-329.
- Букатов А.Е., Букатов А.А., Жарков В.В. и др. Распространение поверхностных волн в ледовых условиях. Севастополь: ФГБУН ФИЦ МГИ; 2019. 204 с.
- Маленко Ж.В., Ярошенко А.А. Изгибно-гравитационные волны в море с ледяным покровом от движущихся возмущений. Морские интеллектуальные технологии. 2021;4(2):157-161.
- Галабурдин А.В. Бесконечная пластина, нагруженная нормальной силой, движущейся по сложной траектории. Advanced Engineering Research (Russia). 2020;20(4):370-381.


