Метод решения задачи расчета надежности сложных систем при переменных параметрах потоков отказов агрегатов

В работах [1–3] предложен метод расчета надежности сложных функциональных систем самолетов гражданской авиации при стационарности потока отказов ω . В соответствии с ним вероятность отказа функциональной системы рассчитывается на дискретных отрезках времени [0, t ].

Для вероятности отказа агрегатов принято следующее распределение равномерной плотности, при котором интегральная функция распределения записывается в виде

q ( t ) = ω ⋅ t . (1)

Распределение с равномерной плотностью вероятности соответствует условию стационарности, накладываемому на пуассоновский поток отказов. Здесь уместно отметить, что на практике потоки отказов функциональных систем более редкие, чем агрегатов, и также пуассоновские.

Приняв t = 1, из выражения (1) можно определить вероятность отказа за 1 ч, как этого требуют нормы летной годности самолетов:

q (1) = ω ⋅ 1 = ω 1 . (2)

Для принятия дискретного отрезка времени [0, t ] протяженностью τ как единичного (например, 3 600 с или продолжительность типового полета самолета) в указанных работах предложено приводить к τ параметр потока отказов, при этом

ω τ = ω ⋅ τ . (3)

Тогда выражение (2) запишется в виде

q (τ) = ω τ ⋅ 1. (4)

При определении вероятности отказа агрегата на отрезке τ, принятом за единичный, интегральная функция определена уже как дискретное событие. Это обеспечивает корректность применения теоремы умножения вероятности для расчета надежности сложной системы.

Для системы с общим резервированием, состоящей из n параллельно включенных подсистем, содержащих по n последовательно соединенных агрегатов, выражение для расчета вероятности отказа записывается в виде

Q c = {1 – [1 – q (τ)] ⁿ } ⁿ . (5)

В отмеченных работах по выражению (5) определяется вероятность отказа системы только на дискретных отрезках времени [0, t ]. Ему не приписываются свойства интегральной функции вероятности отказа системы.

В монографии [4] отмечается, что даже у обслуживаемых (восстанавливаемых) агрегатов потоки отказов могут быть медленно меняющимися во времени, т. е. ω = var . При работе необслуживаемых систем, имеющих различные виды резервирования (горячий резерв, холодный резерв, скользящее резервирование), потоки отказов агрегатов, естественно, возрастают по мере увеличения наработки. В связи с этим задача построения решения для расчета надежности системы при переменных по времени параметрах потоков отказов агрегатов является актуальной.

Для решения поставленной задачи необходимо заменить на единичном отрезке времени [0, t ] переменный параметр потока отказов эквивалентным постоянным. Для этого можно использовать метод, разработанный в [1–3]. В теории колебаний для решения задачи с нелинейным трением широко применяется метод эквивалентной линеаризации. В ряде случаев нелинейные дифференциальные уравнения с нелинейным диссипативным звеном не имеют решения. Для приведения таких уравнений к линейным дифференциальным уравнениям и используется этот метод.

Нелинейное диссипативное звено заменяют линейным при условии равенства диссипируемой энергии колебаний при одинаковой амплитуде колебаний.

В рассматриваемой работе предлагается метод замены на отрезке времени [0, t ] переменного параметра потока отказов ю ( t ) постоянным ю _э при условии равенства вероятности отказа агрегата q ( t ) при постоянном и переменном параметрах потоков отказов (рис. 1).

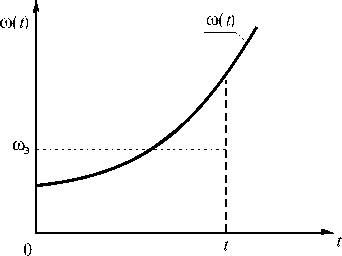
Рис. 1. Замена переменного параметра потока отказов ю ( t ) постоянным ю_э

Интегральная функция вероятности отказа агрегата вида (1) предполагает параметр потока отказов ю численно равным плотности вероятности распределения с равномерной плотностью. Тогда условие эквивалентности ю ( t ) и ю _э на отрезке [0, t ] определится в виде

t

юэ ■ t = J ю(т)dт ,                     (6)

о откуда

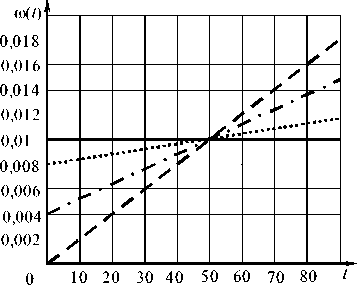
Рис. 2. Пример зависимостей параметра потока

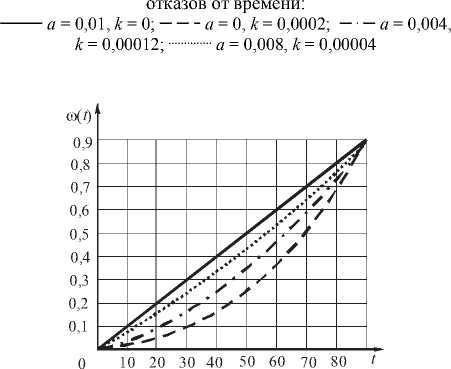
Рис. 3. Интегральные функции распределения вероятности отказа агрегата, построенные методом эквивалентной линеаризации:

----а = 0,01, к = 0;--- а = 0, к = 0,0002;--- а = 0,004, к = 0,00012;............ а = 0,008, к = 0,00004

t

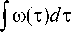
ю э =     ----.                       (7)

В левой части равенства (6) ю _э принимается постоянным на отрезке времени [0, t ]. Вместе с этим при изменении протяженности отрезка [0, t ] изменяется и величина ю э . Но в пределах рассматриваемого отрезка [0, t ] запись ю э ■ t означает не что иное, как определение вероятности отказа на отрезке при распределении с равномерной плотностью вероятности. Это обеспечивает возможность построения для агрегата интегральной функции распределения вероятности отказа, если задаться различными значениями протяженности отрезка [0, t ].

В качестве иллюстрации предлагаемого метода (рис. 2) приведены различные реализации переменного значения параметра потока отказов ю ( t ) в виде

ю ( t ) = a + kt                    (9)

для ряда значений a и k .

Для рассматриваемого примера приведены интегральные функции распределения вероятности отказа агрегата, построенные в соответствии с предложенным методом эквивалентной линеаризации (рис. 3).

Разработанный метод эквивалентной линеаризации обеспечивает возможность решения задачи расчета надежности сложных функциональных систем, приведенных в работах [1-3] для случая, когда параметры потоков отказов агрегатов переменны во времени.