Метод Ритца при дискретной аппроксимации перемещений для расчета плит мостовых сооружений, подкрепленных ребрами различной формы

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2025PNRPU MECHANICS BULLETIN

Плиты, подкрепленные ребрами жесткости, находят применение во многих сферах инженерной деятельности. Широкое распространение такие конструкции получили среди мостовых сооружений и гражданских зданий и сооружений. Ребристые плиты позволяют перекрывать более значительные пролеты, чем плиты, не имеющие ребер жесткости [1]. Граничные условия в виде жесткого защемления по двум противоположным граням при свободных двух других гранях часто можно встретить при однопролетной схеме работы мостовых конструкций. Среди них можно отметить такие конструктивные системы, являющиеся жестко защемленными ребристыми плитами, как арочные, рамные балочные мосты и путепроводы типа «Бегущая лань» с V-образными опорами [2–5]. В промышленном и гражданском строительстве тоже часто можно встретить плиты, подкрепленные ребрами жесткости. Ребристые перекрытия и покрытия зданий можно назвать классическим решением, обеспечивающим значительную экономию материалов по сравнению с плитами без ребер [6].

Чаще всего для расчета напряженно-деформированного состояния (НДС) плит используется метод конечных элементов (МКЭ) [7]. Однако численные методы расчета плит и оболочек разнообразны и активно развиваются [8; 9]. Некоторые из методов расчета основаны на разбиении области на элементы (метод конечных элементов [7], метод конечных разностей [10]), другие требуют только узлов (бессеточные методы [11]), третьи можно назвать полуаналитическими (метод дифференциальных квадратур [12]), четвертые позволяют найти точное решение краевой задачи при определенных упрощениях (метод конструктивной анизотропии [13; 14]). Иногда плиту, подкрепленную ребрами, допустимо рассматривать как осесимметричную [15], что можно считать одной из наиболее простых методик расчета.

Метод Л.В. Канторовича достаточно широко используется применительно к плоским плитам [16–19]. Этот метод позволяет понизить мерность задачи и свести двумерный функционал к одномерному, что значительно упрощает расчет. Ранее автором совместно с В.В. Карповым метод Л.В. Канторовича был применен к ребристым плитам [15]. Однако минимум полученного одномерного функционала находился аналитически, при помощи метода конструктивной анизотропии, при котором ребристая плита приводилась к эквивалентной плите постоянной толщины. В данной же статье учитывается дискретное расположение ребер. Поэтому в дополнение к методу Л.В. Канторовича применяется метод Ритца, который часто используется при расчетах плит [20; 21].

Распространенным математическим способом учета дискретного расположения ребер жесткости являются единичные столбчатые функции и дельта-функции [22– 25]. Эти функции, включенные в функционал, позволяют учесть местоположение ребер и, при необходимости, изменение их геометрических характеристик по длине. В настоящем исследовании применялись единичные столбчатые функции и анализировалось удобство их применения и сходимость решения с таковым, полученным с помощью метода конструктивной анизотропии при точном решении краевой задачи для обыкновенных дифференциальных уравнений (в дальнейшем будем говорить «ранее полученное решение»).

Целью статьи является разработка оптимальной с точки зрения трудоемкости и при этом точной методики расчета прямоугольных плит, подкрепленных ребрами жесткости и опертых по двум противоположным сторонам. Для этого объединены метод Ритца при дискретной аппроксимации перемещений и метод Канторовича.

Общий вид рассматриваемой плиты

На рис. 1 представлен общий вид рассматриваемой плиты и направления координатных осей. Будем считать, что при у = 0, y = b плита жестко закреплена, а при x = 0, x = а она свободна. Ребра расположены в одном направлении, параллельно оси 0 y .

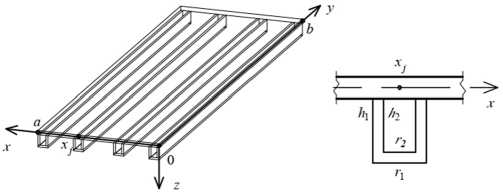
Рис. 1 Общий вид рассматриваемых плит

Fig. 1 General view of the plates under consideration

Функционал полной потенциальной энергии

Рассматриваются жесткие плиты, допускающие малые перемещения, для которых справедлива гипотеза прямых нормалей. Вывод функционала полной потенциальной энергии таких плит выполнен ранее в статье [15], поэтому здесь не приводится. По аналогии с [15], к функционалу полной потенциальной энергии деформации плиты применен метод Л.В. Канторовича. В соответствии с краевыми условиями при y = 0 и y = b разложение функции прогиба W принято в виде [26; 27]:

W ( x , У ) = f ( x ) sin 2 [ ^{П У} v b

Здесь W – перемещение плиты в направлении оси z .

Запишем финальный вид функционала:

a

E s =        П ! a ( f ) ^{+ a} 2 f 2 ^{+ a} з f f ^{+ a} 4 ( f ^ - ² q 2 f 1 “x , ⁽¹⁾

• ²    ( 1 - ^ц ) 0

где

3b a d , 181

π4             π2

a^    2 ~ d , a^ d-j ,

2 _b 3   23_{2 b} 3

a

π2

d ₄, 2 b

b q 2 = 2 qi,

h ³

= Jr +-- , “ 2 = Jv

1 x 12     2 y h3

d 3 = ц ( d 1 + d ₂ ) ,

d 4 = 2 (1 - ') [ J + h- ^ , q i = J' q. v 12 J           E

Jx , Jy – моменты инерции сечения ребер в направлениях x и у соответственно (0 <  x <  a , 0 <  у <  b ),

Jxy = 2 (Jx + J у ) , E, ' - модуль упругости и коэффици- ент Пуассона материала плиты, f – неизвестные функции, аппроксимирующие функцию прогибов W, зависящие от x, a – ширина плиты в направлении x, b – длина плиты в направлении y, h – толщина плиты.

Минимизация функционала (1) должна проводиться при краевых условиях при x = 0, x = a . Получение краевых условий при x = 0, x = a из условия минимума функционала полной потенциальной энергии приведено в [15]. Они имеют вид:

2 a 1 f ' + a 3 f = 0, 2 a 1 f "+( a 3 - 2 a ₄ ) f ' = 0.     (2)

Типы ребер и их жесткостные характеристики

Ребра расположены вдоль свободных граней плит (ось 0 y ) и имеют одинаковые размеры. На рис. 2–5 показаны варианты ребер. Используется уточненный дискретный метод ввода ребер жесткости [14; 28]. Для этого применяются единичные столбчатые функции, равные разности двух единичных функций [14], которые обозначаются 5 ( x - x j ) .

Вариант I (см. рис. 2).

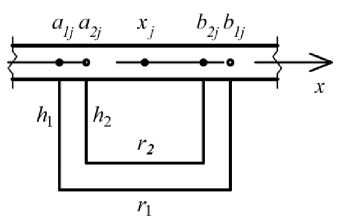
Рис. 2. Ребро коробчатого сечения

Fig. 2. s tiffener in the shape of a box

Моменты инерции для ребра коробчатого сечения:

Моменты инерции для ребра таврового сечения:

^m rr

Jx = E J1-51 ( x - xj )-J2-82 ( x - xj )

j “ i L    a                    a ^{x 7}

J_x = _E J 1 - $ ( x - x , ) + J21 8 2 ( x - x , )

“! L a '       ⁷ a ^{x 7}

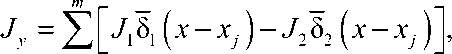
j = i

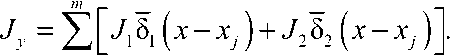
j = i

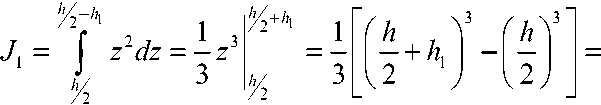
Вариант IV (см. рис. 5).

h ₁

h 7 I h

2 + hi I + 2 (h + hi)

2 2 _h

J2 = j z dz = — h3

h 7 I h

+ h + (h + h

2 21

Здесь и далее в формулах обозначено:

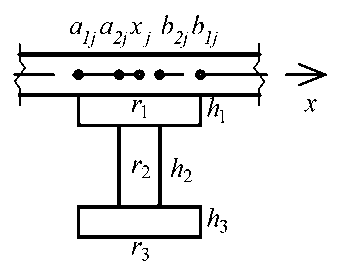
Рис. 5. Ребро двутаврового сечения

5i (x-xj ) = U(x-aij )-U(x-bij ), 82 (x - xj) = U (x - a 2 j) - U (x - b2 j), $3 ( x - xj ) = U ( x - a3 j)-U ( x - b3 j) ,

Fig. 5. s tiffener in the shape of an I-beam

Моменты инерции для ребра двутаврового сечения:

a i j = x j

rr

2’ bi j = xj + 2’ a 2j= xj

^{r 2} , b 2²

r ₂

2,

-m    r

)

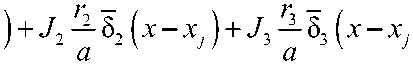
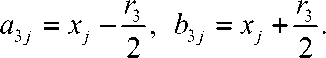
^Jx = E ^J i- § ( x ^- x j , = i L    ^a

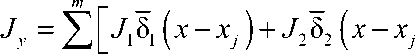
j = i

) + J3 §3 (x - xj )].

Вариант II (см. рис. 3).

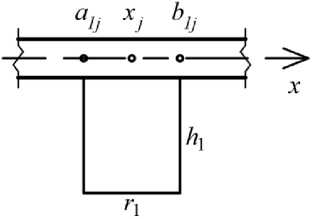
Рис. 3. Ребро сплошного сечения

Для вариантов II – IV:

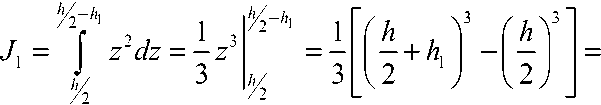
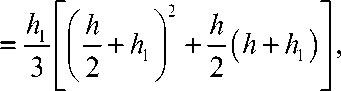
h 2 ⁺ h i ⁺ h 2             j      h2 + h _i + h 2

J 2 =    j   z² dz = —z³

h 2 + h _i             ³     h 2 ⁺ h i

Fig. 3. s tiffener in the shape of a solid rectangular section

Моменты инерции для ребра сплошного сечения:

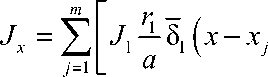
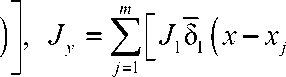
) J

( h 1 7 I ³ ( h 7 I ³ ^ 2 ⁺ h i ^{+ h} 2 I - ^ 2 ⁺ h i I

Вариант III (см. рис. 4).

h ₂

h + hi + h 2 | + (2 + h | (h + 2 hi + h 2)

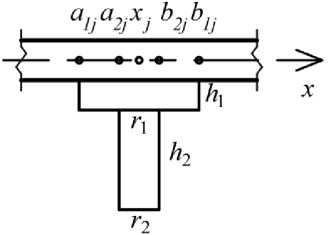
Рис. 4. Ребро таврового сечения

^h/2 ⁺ h i ⁺ h ₂ ⁺ h 3                   h / + h _i + h ₂ + h₃

J ₃ =     j    z² dz = —z³

h 2 + h _i + h ₂              ³ h 2 ⁺ h i ^{+ h}2

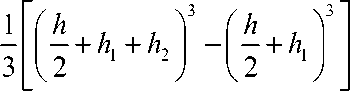
Fig. 4. s tiffener in the shape of a T-beam

h

2 ⁺ h i ^{+ h} 2 ^{+ h} 3 |

2 + h_i + h ₂ 1 ( h + 2 h_i + 2 h ₂ + h ₃ ) .

Применение метода Ритца при дискретной аппроксимации перемещений (МРДАП) для одномерного функционала

Для минимизации функционала (1) при краевых условиях (2) и нахождения прогиба W ( x ) применялся метод Ритца при дискретной аппроксимации перемещений. Отрезок [0, a ] разбивается на n частей точками x i , которые будем называть узловыми (рис. 6). Обозначим x_t - x i - 1 = А .

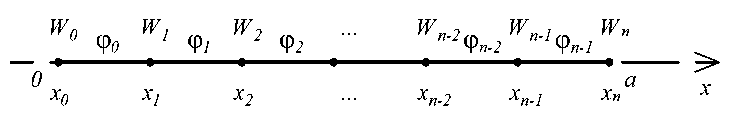
Рис. 6. Разбиение отрезка [0, a ] узловыми точками

Fig. 6. Partition of the segment [0, a ] by nodal points

a

b

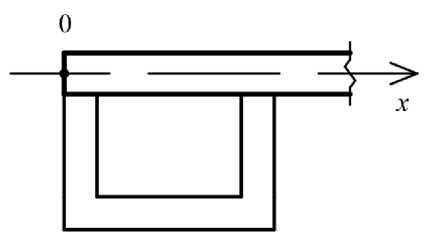
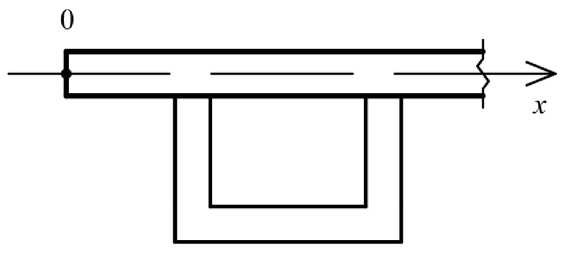
Рис. 7. Ребра у края плиты

Отрезки [ x i -1 , x i ] по аналогии с методом конечных элементов будем называть конечными элементами (КЭ). На каждом конечном элементе функция W ( x ) аппроксимировалась многочленом третьей степени:

Ф i ( x ) = b_{0 i} + b 1i x + b_{2 i} x ² + b_{3 i} x ³. (3)

Из непрерывности прогибов W ( x ) и углов поворотов W’ ( x ) в узловых точках для примыкающих к узлу конечных элементов получается зависимость функций ф i ( x ) от перемещений и углов поворотов. Эти условия записываются в виде:

ф,(xM) = W_1, ф'(xw) = W-„ ф,(x,) = W, ф'(x) = W

Для формирования системы линейных алгебраических уравнений, из решения которой находятся все W i и W' , находятся производные от функционала (1) по W i и W i' , и приравниваются нулю. Эта операция проводится для каждого внутреннего узла x i . Внутренних узлов будет n – 1, то есть уравнений будет 2 n – 2. Недостающие уравнения получаются при использовании двух краевых условий в точках x = 0, x = a.

Краевые условия при дискретной аппроксимации перемещений

Так как в коэффициентах a 1 – a 4 уравнений (2) содержатся единичные столбчатые функции, а сами краевые условия (2) задаются не в интегральной форме, то жест-костные характеристики ребер в (2) задаются с использованием следующих предпосылок:

– если элемент ребра (стенка или полка) попадает в крайнюю точку отрезка [0, a ], в которой рассматриваются граничные условия, то жесткостные характеристики этого элемента учитываются при составлении уравнений (рис. 7, a );

– если элемент ребра не попадает в соответствующую точку, то его характеристики не учитываются (рис . 7, b ).

• Fig. 7.    s tiffener at the edge of the plate

Из краевых условий (2) получаются четыре недостающие уравнения. Производные в краевых условиях (2) получаются путем дифференцирования функций (3).

Учет ребер при помощи единичных столбчатых функций

В функционале (1) коэффициенты d 1 – d 4 и соответственно a 1 – a 4 зависят от обобщенных функций. Поэтому элементы функционала можно разделить на зависящие от ребер и не зависящие. Таким образом, функционал (1) можно представить в виде:

a

E s = f A o ( f ) - 2 q 2 f + EE A k ( f )⁵ k (

0 L                         k = 1 j = 1

-

:j ) d ^x , ⁽⁴⁾

где A 0 ( f ) – оператор функции f , включающий в себя элементы обшивки; A k ( f ) – операторы функции f , зависящие от ребер, m – количество ребер, n – количество входящих в моменты инерции параметров J 1 , J 2 , J 3 .

При использовании единичных столбчатых функций 5 ( x - x j ) интеграл на отрезке [ x i -1 , x i ], если он пересекает участок, определяющий ребро j , [ a 1 ,j , b 1 ,j ], в функционале (4) примет следующий вид:

xi                                              a2,j f Ak(f)5k (x - xj)dx = f Ak(f) dx. xi-1                                                 a1, j

Если отрезки [xi-1, xi] и [a1,j, b1,j] не пересекаются, то xi f A1( f)51 (x - xj)dx = 0.

x i - 1

На рис. 8 крестообразной штриховкой показана область пересечения конечного элемента и единичной столбчатой функции ребра.

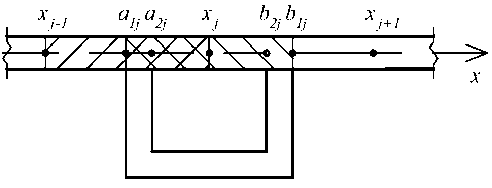
Рис. 8. Пересечение конечного элемента и ребра

• Fig. 8.    Intersection of a finite element and a stiffener

Было рассмотрено два способа вычисления жест-костных характеристик ребер. Покажем на примере ребер варианта I:

• •    Тип 1. Интегралы, образованные каждой столбчатой функцией, вычислялись в соответствии с пределами интегрирования этой функции:

xi f [ A1( f )8 ( x - xj)-A2 (f )82 ( x - xj ) ] dx = xi--1

x j x j

= f A i ( f ) dx — f A ( f ) dx .

^a 1, j^a 2, j

• •    Тип 2. Пределы интегрирования образованных столбчатыми функциями одного ребра интегралов выбираются по максимальной ширине элемента (чаще всего это ширина полки). Учет ширины остальных элементов (стенка, нижняя полка) осуществляется при помощи отношения ширины элемента к наибольшей ширине. Интеграл примет вид:

f ^[ A ^{( f} ) 8 1 ( x ^- x j)^- A ⁽ f )§ 2 ( x ^- x j) ] dx = ^xi - 1

= f A 1 ( f ) dx - f r^ A ( f ) dx .

^a 1, j                       ^a 1, j ^{r 1}

Численный эксперимент

Для апробации методики рассматривались конкретные размеры плиты, материал и нагрузка. Общий вид такой плиты был показан на рис. 1. Исходные данные: a = 6 м, b = 40 м, h = 0,2 м, q = 10^-2 МПа (240 т на всю плиту), E = 4∙10⁴ МПа, μ = 0,2. Плита в направлении оси 0 y равномерно подкреплена четырьмя ребрами одинакового размера, причем крайние ребра являются контурными (см. рис. 7, а ), поэтому в краевых условиях учитывалась их жесткость. Площадь поперечного сечения всех ребер одинаковая и равна 0,15 м². В табл. 1 указаны геометрические характеристики ребер. Разбиение отрезка [0, a ] на конечные элементы выполнялось таким образом, чтобы узлы попадали в крайнюю и центральную точку ребер.

В табл. 2 приведены перемещения в центре плиты с ребрами коробчатого сечения, полученные в результате расчета. В табл. 3 приведены перемещения в центре плиты с ребрами сплошного сечения, полученные в результате расчета.

В табл. 4 приведены перемещения в центре плиты с ребрами таврового сечения, полученные в результате расчета. В табл. 5 приведены перемещения в центре плиты с ребрами двутаврового сечения, полученные в результате расчета.

Таблица 1

Геометрические характеристики ребер

Table 1

Geometric characteristics of stiffeners

Номер варианта	I	II	III	IV
Графическое отображение	A A r2		I n 1 ^ A	1 П J ^ >2 A 1__________1*3 A
Размеры ребер	h 1 = 0,6 м h 2 = 0,5 м r 1 = 0,5 м r 2 = 0,3 м	h 1 = 0,5 м r 1 = 0,3 м	h 1 = 0,1 м h 2 = 0,75 м r 1 = 0,75 м r 2 = 0,1 м	h 1 = 0,1 м h 2 = 0,5 м h 3 = 0,1 м r 1 = 0,5 м r 2 = 0,1 м r 3 = 0,5 м

Таблица 2

Ребро коробчатого сечения (Вариант I)

Table 2

Stiffener in the shape of a box (Version 1)

Количество КЭ по ширине ребра	Всего элементов по ширине	Перемещение в центре плиты, мм		Ранее полученное решение, мм	Относительная разница с ранее полученным решением, %
		Тип 1	Тип 2		Тип 1	Тип 2
2	24	-3,15	70,26	64,87	104,8	6,1
4	48	-0,17	68,80		100,3	3,8
6	72	69,24	68,35		4,5	3,2
8	96	68,83	68,12		3,9	2,8
10	120	68,59	67,99		3,5	2,6
20	240	68,11	67,76		2,8	2,3
40	480	68,35	68,08		3,2	2,8

Таблица 3

Сплошное прямоугольное ребро (Вариант II)

Table 3

Stiffener in the shape of a solid rectangular section (Version 2)

Количество КЭ по ширине ребра	Всего элементов по ширине	Перемещение в центре плиты, мм		Ранее полученное решение, мм	Относительная разница с ранее полученным решением, %
		Тип 1	Тип 2		Тип 1	Тип 2
2	24	114,7	114,7	64,87	6,2	6,2
4	48	113,4	113,4		5,0	5,0
6	72	113,0	113,0		4,6	4,6
8	96	112,8	112,8		4,4	4,4
10	120	112,7	112,7		4,3	4,3
20	240	112,6	112,6		4,3	4,3
40	480	119,8	119,8		10,9	10,9

Таблица 4

Тавровое ребро (Вариант III)

Table 4

Stiffener in the shape of a T-beam (Version 3)

Количество КЭ по ширине ребра	Всего элементов по ширине	Перемещение в центре плиты, мм		Ранее полученное решение, мм	Относительная разница с ранее полученным решением, %
		Тип 1	Тип 2		Тип 1	Тип 2
2	24	4,76	78,69	64,87	94,0	0,5
4	48	87,36	80,75		10,4	2,1
6	72	88,48	81,45		11,8	3,0
8	96	88,90	81,80		12,4	3,4
10	120	89,24	82,01		12,8	3,7
20	240	90,28	82,44		14,1	4,2
40	480	90,78	82,51		14,8	4,3

Таблица 5

Двутавровое ребро (Вариант IV)

Table 5

Stiffener in the shape of an I-beam (Version 4)

Количество КЭ по ширине ребра	Всего элементов по ширине	Перемещение в центре плиты, мм		Ранее полученное решение, мм	Относительная разница с ранее полученным решением, %
		Тип 1	Тип 2		Тип 1	Тип 2
2	24	5,60	61,52	64,87	90,5	5,0
4	48	61,05	60,88		4,2	3,9
6	72	60,94	60,68		4,0	3,6
8	96	60,88	60,58		3,9	3,4
10	120	60,90	60,52		3,9	3,3
20	240	58,28	60,41		0,5	3,1
40	480	61,55	60,97		5,0	4,0

На рис. 9 и 10 показано сравнение прогибов центральной части плиты вдоль оси 0 x , полученных методом конструктивной анизотропии и предложенным в статье методом.

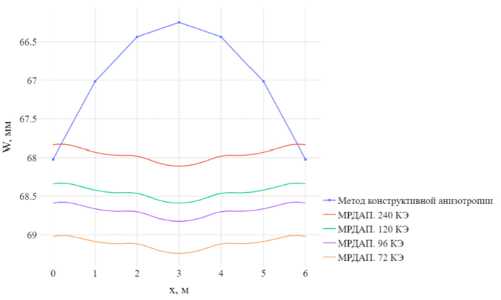
Рис. 9. Сравнение с методом конструктивной анизотропии. Ребра: Вариант 1, тип решения 1

• Fig. 9.    Comparison with the constructive anisotropy method. stiffeners: Version 1, solution type 1

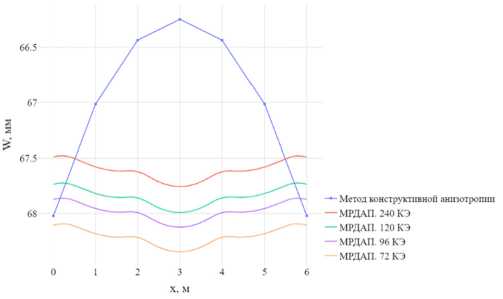
Рис. 10. Сравнение с методом конструктивной анизотропии.

Ребра: Вариант 1, тип решения 2

• Fig. 10.    Comparison with the constructive anisotropy method.

Stiffeners: Version 1, solution type 2

Обсуждение и заключение

Разработана методика расчета ребристых плит, подкрепленных по двум противолежащим сторонам.

На основе вычислительного эксперимента с четырьмя видами ребер различной конфигурации можно сделать следующие выводы.

В рассмотренном численном эксперименте оптимальное количество КЭ по ширине ребра равно 6, при этом общее число КЭ на отрезке 6 м при разных видах ребер разное, но не менее 48 для ребер таврового сечения и не более 120 для ребер сплошного сечения.

Во всех случаях отмечается небольшое (порядка 2–5 %) расхождение решения, полученное предложенным в статье методом от ранее полученного решения (метод конструктивной анизотропии). Здесь на 6 м длины отрезка интегрирования приходится 4 м контакта ребер с обшивкой. Следовательно, при отношении суммарной ширины ребер к ширине плиты а , равном 1:3 и более, можно использовать метод конструктивной анизотропии.

На рис. 9 и 10 видно, что характер деформаций в направлении оси 0 x при расчетах методом конструктивной анизотропии и методом дискретной аппроксимации перемещений отличаются. Наибольший прогиб при расчете методом конструктивной анизотропии достигается на краю плиты. При расчете методом дискретной аппроксимации максимальный прогиб в центре. Это объясняется тем, что при расчетах методом конструктивной анизотропии плита деформируется как гладкая, имеющая эквивалентную ребристой жесткость. При использовании метода дискретной аппроксимации плита имеет максимальные прогибы в центре, между ребрами, что больше соответствует действительной работе конструкции.

Было рассмотрено два типа вычисления жесткостных характеристик ребер. По первому типу, когда ребра коробчатого вида, в виде двутавра и тавра, только первая единичная функция при х = 0 не равна нулю, а остальные равны нулю, поэтому неверно будут заданы краевые условия и в результате решение получается с ошибкой. По второму типу жесткостные характеристики контурных ребер учитываются верно, поэтому при разбиении ребра на две части решение сразу начинает сходиться к точному.