Метод сильного улучшения управления для неоднородных дискретных систем

Системы неоднородной структуры, т.е. процессы с изменяющимся во времени описанием, как непрерывные, так и дискретные, широко распространены на практике. Примерами могут служить сложные космические операции (например, перелет между планетами), динамика роботов, процессы химического производства, развитие организмов и популяций. Описание некоторых из них приведено в [1] . Далее будут рассматриваться неоднородные дискретные процессы (НДС).

Поскольку непосредственное использование необходимых и достаточных условий оптимальности для различных типов управляемых систем не представляется возможным из-за трудностей разрешимости в аналитическом виде содержащихся в них соотношений, то внимание исследователей всегда было сосредоточено на построении на их основе разнообразных итерационных методов. При этом следует заметить, что львиная доля таких методов позволяет найти лишь локальный, а не глобальный минимум функционала. Подобные методы более просты как в их разработке, так и реализации.

В классической задаче оптимального управления для непрерывных систем различают сильный и слабый относительный минимум [2] . Итак, пусть z = (x, u), где x — состояние, a u — управление, элемент из класса допустимых, на котором функционал достигает относительного минимума. Будем называть такой относительный минимум сильным, если он достигается среди элементов z, удовлетворяющих условию | x — х | < е. И в свою очередь слабым, если он достигается среди элементов z , удовлетворяющих условиям | x — х | < е, | u — и | < е.

В дискретных системах в силу специфики их структуры говорят просто об относительном минимуме, который по своей сути является слабым [2] . Здесь достаточно требования близости элементов по управлению, из которого автоматически следует близость по состоянию.

Если же речь идет об управляемых системах неоднородной структуры, которые являются двухуровневыми, где на нижнем уровне чередуются непрерывные системы, а на верхнем — дискретные (ДНС), естественным для нижнего уровня будет требование близости элементов, как только по состоянию, так по состоянию и управлению. Для верхнего уровня только по управлению. По схеме: на нижнем близость по состоянию, на верхнем — по управлению, был построен метод улучшения в [3] . Когда же оба уровня дискретные (НДС), то по аналогии с классикой можно говорить о близости по управлению на обоих уровнях.

И все же возникает естественный вопрос: а можно ли для НДС построить метод, в котором на обоих уровнях элементы близки лишь по состоянию и будет ли этот метод работоспособным. Далее в статье рассматривается именно эта ситуация.

При постановке задачи оптимального управления использовалась математическая модель НДС с промежуточными критериями из [4] , а для построения метода — аналог достаточных условий оптимальности Кротова, полученный в этой же работе.

1.    Неоднородные дискретные процессы с промежуточными критериями

Рассмотрим двухуровневую модель, в которой нижний уровень составляют дискретные динамические системы однородной структуры. На верхнем уровне фигурирует дискретная модель общего вида (1)                          x(k + 1) = f (k,x(k'),u(k')'), k G K = {kI,kI + 1,...,kF}, u G U(k,x), где k — номер шага (этапа), x и u — соответственно переменные состояния и управления произвольной природы (возможно различной) для различных k, U(k,x) — заданное при каждом k и x множество.

На некотором подмножестве K ‘ С K , k F / K ‘ , u(k) интерпретируется как пара (u v (k), m d (k) , где m d (k) — процесс (x^d(k,t),u^d(k,t)), t G T (k,z(k)), m ^d (k) G D d (k,z(k)), а D d — множество допустимых процессов m ^d , удовлетворяющих системе

(2)                 xd(k, t + 1) = fd (k, z, t, xd(k, t),ud(k, t)) , t G T = {ti (z),ti (z) + 1,...,tF (z)}, xd G Xd(k,z,t), ud G Ud (k,z,t,xd) , z = (k,x,uv) .

Здесь u ^v управляющее воздействие верхнего уровня на нижний. Для этой системы на множестве T задана промежуточная цель в виде функционала, который необходимо минимизировать:

I k = E f k (t,x ^d (k,t),u ^d (k,t)) ^ inf .

T ( z ) \ t F ( z )

Здесь X ^d (k,z,t), U d (k,z, t, x ^d — заданные при каждом t , z и x ^d множества. Оператор правой части (1) сводится к следующему:

f (k, x,u) = в (z, Yd(z)) , Yd = (ti ,xi, tF ,xdF) G rd(k, z), rd(z) = {Yd: ti = т(k,z), tF = ^(k,z), xd = ^(k,z), xF G rdF(k,z)}, где θ и τ , ϑ, ξ — заданные оператор и функции.

На множестве D процессов m = (x(k), u(k),xd(k, t),ud(k, t)) , удовлетворяющих (1), (2), рассматривается задача оптимального управления о минимизации концевого функционала I = F (x (kF)) при фиксированных ki = 0, kF, x(ki) и дополнительных ограничениях x(k) е X(k).

2.    Используемый математический аппарат

Далее для удобства читателей приведем используемые для построения метода конструкции и теоремы.

Имеем [4] :

L = G (x (k F )) — ^ R(k,x(k'),u(k')') + K \ K ‘ \ k F

+ Y^G d Z) — E R d (z,t,x ^d (k,t),u ^d (k,t^ K ‘              T (z) \ t F

G(x(k F )) = F((x(k F )) + ф (k F ,x(k F )) — ф (k i ,x (k i )),

R (k,x,u) = ф (k + 1, f (k, x, u)) — ф (k, x),

G ^d (k, z, y ^d ) = —ф (k + 1,9 (k, z, Y d )) + ф (k, x(k)) +

• + ф ^d (k, z, t F , x F ) — ф ^d (k, z, t i ,x^d) , R d (k, z, t, x ^d , u ^d ) = ф^а ((k, z,t + 1, f ^d (k, z, t, x ^d , u ^d )) —

• — f k (t,x ^d (k,t),u ^d (k,t) — ф ^d (k,z,t,x ^d ),

V d (k, z, t) = sup {R d (ki, z, t, x ^d , u ^d ) : x ^d е X ^d (k, z, t),u ^d е U d (k, z, t, x^d){, l ^d (k, z) = inf {G ^d (k, z, y ^{d )} : Y d е r ^d (k, z), x ^d е X ^d (k, z, t F )},

V (k)

{sup {R (k, x,u) : x е X(k), u е U (k, x)}, — inf {ld (z) : x е X (k) , uv е Uv (k, x)}, t е k\k', k е K',

l = inf {G (x) : x е Г П X (k _F )}.

Здесь ф (k,x) — произвольный функционал, ф ^d (k,z,t,x^d') — произвольное параметрическое семейство функционалов (с параметрами k , z ). В дальнейшем указанные функционалы φ, φ ^d подлежат определению.

Теорема 1. Для любого элемента m е D и любых ф, фd имеет место оценка

I(m) — inf I <  A = I(m) — l.

Пусть имеются два процесса m ¹ G D и m¹¹ G E и функции ф и ф ^d такие, что L (m¹¹) <  L (m¹) = I (m¹) , и m ¹ G D .

Тогда I (m ¹¹ ) <  I(m¹).

Здесь E — множество, включающее в себя множество D , [2] .

Теорема 2. Пусть имеются последовательность процессов { m _s } ⊂ ⊂ D и функционалы φ, φ ^d , такие что:

• 1)    R (k, xs(k),u_s(k}) ^ [j, (k) , k G K;

• 2)    Rd (zs,t,xd(t),ud(t)) - j^d(zs,t) ^ 0, k G K‘, t G T (zs);

• 3)    G^d (z^d) - l^d(zs) ^ 0, k G K‘;

• 4)    G (xs (tF)) ^ l.

3.    Метод улучшения

Тогда последовательность { m _s } — минимизирующая для I на D .

Здесь и ниже предполагается, что все используемые объекты обладают необходимыми для выполняемых операций свойствами, такими как непрерывность, дифференцируемость и т.д.

Предположим, что X (k) = R ^m(k) , X ^d (z,t) = R ^n(k) , x I = ^ (z), k _I , x _I , k F , t I (k), t _F (k) — заданы, x F G R ^n(k) и системы нижнего уровня не зависят от управления u ^v . Последнее требование позволяет избежать излишней громоздкости метода. Рассматриваемая далее задача улучшения состоит, по существу, в построении оператора 0(m), 6 : D ^ D , такого что I(0(m)) <  I(m) [4] . При некотором заданном начальном элементе такой оператор генерирует улучшающую, в частности, минимизирующую последовательность {m s } : m s₊₁ = 0(m _s ).

Будем строить метод на основе принципов расширения [5] и локализации [6] . Согласно последнему, задача улучшения некоторого элемента m ¹ сводится к задаче о минимуме вспомогательного функционала

• (3)            I _a (m) = aI(m) + (1 — a)J(m\m), a G [0, 1],

где J(m¹,m) — функционал типа метрики. Изменяя а от 0 к 1, можно достичь необходимой степени близости m _a к m и эффективно использовать аппроксимации конструкций достаточных условий в окрестности m ¹ . В итоге получается алгоритм с параметром а, играющим роль регулятора, настраиваемого при конкретном применении. Этот параметр выбирается так, чтобы разность I(m ¹ ) — I(m_a) была наибольшей, тогда соответствующий элемент m _a принимается за m ¹¹ .

Вспомогательный функционал зададим в виде:

Ia = al +2(1 - a) l£ |Ax (k) |2 + £ £ |Axd (k,t) |2 | , \K\K‘                K‘ T(z)\tF               / где a G [0,1], Ax = x — xI, Axd = xd — xdI. Из выше приведенной формулы следует, что в данном случае функционал J(mI,m) представляет собой половину квадрата по состояниям процесса.

Согласно указанному принципу расширения по заданному элементу m I G D требуется найти элемент m II G D , на котором I _a (m II ) = L _a (m II) < <  I _a (m ) = L _a (mI) , или L _a (m II) — L _a (mI) < 0. Рассмотрим приращение функционала L _a (m), по формуле Тейлора имеем:

AL a - GIF Ax f + 2ax F G x f X F Ax f —

• —   £  ^R T Ax + R T Au + ^-Au ^T R _UU Au + ^Ax^TR _XX Ax +

K \ K ‘ \ k F

• +    Ax^RxUAu \ + £ (,GXTAxd + GdT Ax + -A(xd)TGdd d Axd + xF   F x       2 F    xF xF

K ^′

• +    A(xd)TGdd x Axf\ — £ (RdT Axd + RdT Ax + RdT Aud + xFxF                      x           x

T ( z ) \ t F

• +    ^AudTRdd dAud + ^AxdTRdd d Axd + AxTRd Ax + u u                  x xxx

• +    A x^dr T R^d d _u d Au ^d + Ax T R Xu d Au ^d + Ax d T R d d x Ax^ ,

где Au = u — u I , Ax = x — x I , Au d = u ^d — u ^dI , Ax ^d = x ^d — x ^dI , Ax F = = x F — x FI , x _F = x(k _F ). Здесь функции R, G, R d , G ^d определены для функционала I _α , а их первые и вторые производные подсчитаны при u = u I (k), x = x I (k), x ^d = x ^dI (k,t), u ^d = u^dI(k,t).

Найдем Au, Au ^d доставляющие максимум выражениям, стоящим под знаками сумм        и       соответственно. Имеем:

K\K‘\kF T(z)\tF d d  dd  dd ud      udud           xdud           xud          .

Тогда Aud = —(RUdud)-1(Rdd + RUdxdAxd + RUdxAx) Аналогично Au = = —(RUU)-1 (Ru + RXUAx). Найденные формулы для приращений управлений обоих уровней подставим в выражение для приращения функционала ALa и выполним необходимые преобразования, итог которых обозначим через AMa. Имеем:

AM a « G T F Ax f + 2^x F G x f X F ^X F -

• ^—   ^  ^(R x ^— R xu (R uu ) ^{1 R} T ^)Ax +

K \ K ‘ \ k F

+ 2^x ^{T (}R xx ^{— R} xu ^(R uu ) ^{1 R} T _u ^{)Ax —} 2 R T ^(R uu ) 1 ^R u \ +

+ VfG dT Ax X + G d T Ax + 1A(x X ) ^T G^X_{d d} Ax X + x F F x        2 F    x F x F    F

K ^′

+ A(x F ) ^T G d _F x f Axf) -

d

R _x d

Rx_{d u d} (R^ u d ) ^-1 R u T )Ax ^d +

T (z) \ t F

+

2^Ax d ^{T (R} x d x d

d R x ^d u ^d

(R du d u d ) ^-1 R x T u d )Ax ^d

+ (R d — R dxu d (R^   R" )Ax +

+ Ax ^T (R xx - R xu d R du d u d ^-1 R Xu d )Ax +

¹ pXT X — 1 X>d \ 2 ^R u ^{d (R} u ^d u ^d !   ^R u ^d .

+ Ax ^T (R xx d - R xu d (R du d u d ) ^-1 R dx d u d )Ax ^X

Зададим функции ф и ф ^Х (z) в виде:

ф = ф ^т (k) x (k) +— Ax ^T (k)a(k)Ax(k), ф ^Х = A ^T (k,t)x(k) + ^ ^XT (k,t)x ^x (k,t) +

+ | Ax ^XT (k, t)^ ^x (k, t)Ax ^X (k, t) + | Ax ^T (k)A(k, t)Ax ^X (k, t) +

G x = 0,   G x. = 0,

G xx = 0, G X d _x d = 0, Gx. = 0,

d

R x ^d

R x - R xu R — u R = 0,

R xx

R xu R^R T = 0,

dd

- R x ^d u ^d (R u ^d u ^d

₎ — 1 _R

d T u ^d

= 0,

d xx ^d

d R xu ^d

X — 1   X T

(R u ^d u ^d )   R x ^d u ^d

= 0.

Расшифровка указанных условий приводит к задаче Коши для НДС относительно ф, фx, A, ст, ctx, Л с начальными условиями на правом конце, в которых E — единичные матрицы соответствующих размеров:

^Y (k F ) = ^-aF x ( k F ) ,

Y(k) = H x - f T ^(k + 1)f u + H xu ) X

X (f T ^(k + 1)f u + (H uu ) ^- 1 H T , k e K \ K ‘ \ k F ,

4^(k F ) = ^-aF x ( k F ) x ( k _F ) + ^{(1 — a)E},

W) = f T ^(k + 1)f x + H xx — f T ^(k + 1)f u + H xu ) X

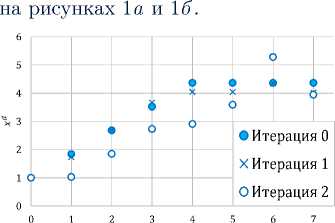
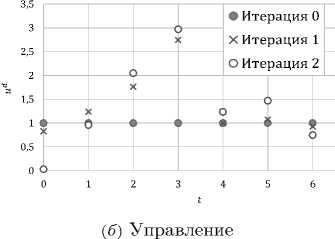
X (fT^(k + 1)fu + HuuY\fT

Yd (k,tF) = Hdd (Y(k + 1)), x_F

^d(k,t) = Hxd + (fxTvd^t + 1)fd + Hxdud )Hdud )-1 HT k e K‘,

^d(k,tF) = 0T ^(k + 1)0,d + Hdd_xd, x_{F            F}x_Fx_F

°^d(k, t) = fY°^d(k, t+f+Hddxd — fT^ t+1fUd +

+ Hxdud) X (,fdT^^d(k,t +1f + HUdud)^-1X

X (fY^Y,t + 1)fdd + HxTud)^T, k e K‘,

Y(k) = Hx(^(k +1)) + \(ti) + £\(ti) — x(tF),

X(k,tF) = Hxf ^(k + 1)),

x(k,t) = HxW(k,t + 1)).

Здесь для краткости в правых частях указаны лишь аргументы Y(k +1) и

Y^d(k,t + 1), необходимые для понимания соотношений.

^(k) = eT^(k + 1)0x + Hxx + gw ^(k + 1)0x+

+ QT^k + 1)0_xd ^x + ^x^Td ^(k + 1)0_xd ^x +

+ £,_x°^d(k,tWx + £x^E(k,tiW л^т (k,tiYT,

^Ek, t) = ^fxd ^E(k, t ^{+ 1)f}x^{T — f}xxd ,

A(k,t_F) = 9xa(k + 1)0_xd + H_xd _x(k,ti),

H (k,^,x^d ,xF) = YT 0(z, x^d, xF), k e K‘,

H^d(k, t, z, Yd, x^d, u^d) = YdTf ^d(k, z, x^d, u^d) —

— f^k(k,z,x^d,u^d) — (1 — a)2\Ax^d(k,t)\2

x(ki )= Xi , x(kF )= XF, Xd(k,ti) = Xd, X^d(k,tF )= xF.

При этом приращения управляющих воздействий имеют вид:

Au(k) = — (.fUfk + 1)fu + HuuT'x x {Hu + ff + f + HfAx(k) ,

Aud(k, t) = - ff, t+if+н^и^ )-1 x x {f + ff, t + if + Hf )TAxd(k, t)+

+ ffk, t + if + Hu fx(k)} .

Замечание 1. Отметим тот факт, что приращения управлений обоих уровней зависят от соответствующих состояний этих же уровней. Следовательно решение поставленной задачи представляет собой линейный приближенный синтез оптимального управления.

Замечание 2. Уравнения для матриц σ и σ^d представляют собой матричные уравнения Риккати, которые могут и не иметь решения. В этом случае алгоритм должен быть дополнен специальной процедурой построения управляющих воздействий. Разработка такой процедуры требует проведения специального исследования и подбора примеров, что выходит за рамки этой статьи.

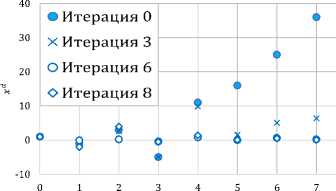
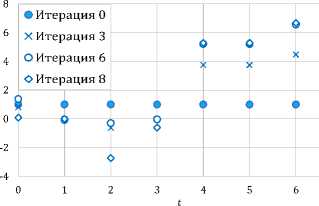
4.    Итерационная процедура

На основе полученных соотношений можно сформулировать следующую итерационную процедуру.

• 1.    «Слева направо» просчитывается НДС (1), (2) при u = us(k), u^d= ud(k, t) и заданных начальных условиях, получается соответствующая траектория (xs(k), x^(k,t)).

• 2.    «Справа налево» разрешается НДС относительно Д (k), Д (k,t), X(k,t),a(k), a^d(k, t), A(k, t).

• 3.    Находятся Au, Au^d и новые управления u = us(k) + Au, u^d= ud(k, t) + Aud.

• 4.    При найденных управлениях и начальном условии x(kI) = XI просчитывается «слева направо» исходная НДС (1), (2). Тем самым определяется новый элемент ms+1 .

5.    Примеры

Процесс итераций заканчивается, когда |Is+₁— Is| ~ 0 с заданной точностью.

Работоспособность построенного метода была проверена на двух иллюстративных примерах. Пример 2 был ранее использован в работе [7] и специально решен предлагаемым методом для сравнения.

Пример 1. Пусть задана НДС, состоящая из двух этапов, обозначенных номерами 0 и 1. На нулевом этапе управляемый процесс описывается одним уравнением:

xd(t + 1) = xd(t) + sin (ud(t)), xd(0) = 1, t = 0,1, 2, 3.

Задан промежуточный функционал этапа:

10 = (ud(t) -1)2.

Следующий первый этап характеризуется другим уравнением и своим промежуточным функционалом:

xd(t + 1) = xd(t)u2(t), t = 4, 5, 6, 1¹= 2((xd(t))² + (ud(t))²).

Задан общий функционал задачи:

I = xd(7) ^ min .

Нетрудно видеть, что K = 0,1, 2, K‘ = 1. Поскольку роль связующей переменной на двух рассматриваемых этапах играет x^d, то в терминах этой переменной легко записать процесс верхнего уровня:

x(0) = xd(0, 0), x(1) = xd(0,4), x(2) = xd(1, 7), xd(1,4) = x(1).

Так как множество K^′состоит из одного элемента, то для удобства расчетов, модель может быть дополнена третьим мгновенным этапом, не имеющим протяженности во времени и состоящим лишь в передачи информации об окончании второго этапа на верхний уровень. Тогда

x(3) = x(2) = xd(1,7), K‘ = 1,2, 0(k) = xd(k,t_F), e(k) = x(k).

Заметим, что на обоих этапах процесс нижнего уровня не зависит от переменных состояния верхнего уровня, тогда

A(0, t) = A(1, t) = 0,   Л(0, t) = Л(1, t) = 0.

Запишем задачу и конструкции в терминах НДС. Имеем: f d(0,t) = xd(t)+sin (ud(t)), f d(1,t) = xd(t)u2(t), fXd (0,t) = 1,                     fXd (1,t) = u2(t), fdd (0,t)=cos (ud(t)) ,         fdd (1,t) = xd (t);

H^d(0, t) = f ^d(0, t +1) (x^d(t) + sin (ud(t))) —

• - (ud^t - t)² - 2⁽¹ - ^a)lл^xd(0,t)|2,

Hdd(0,t) = f^d(0,t + 1),                     Hddxd (0,t) = a - 1,

Hdd(0,t) = ^^d(0,t + 1)cos (ud(t)) +2(t - ud(t)), H^(0,t) = -f^d(0,t +1)sin (ud(t)) - 2,   Hbud(0,t) = 0;

H ^d(1,t) = ^^d(1,t+1)_Xd(t)ud(t)-2((x^d(t))2+(ud(t))²)-2(1-a)^x^d(1,t)p,

H^d_d(1,t) = f^d(1,t + 1)u2(t) - x^d(t),   HXdxd(1,t) = a - 2,

Hdd(1,t) = -2f^d(1,t + 1)(t - ud(t)) - 1,

HUddud (1,t) = -1,                           Hdd_ud (1,t) = f^d(1,t + 1).

Управляющие воздействия являются результатом решения следующих уравнений:

f(2) = f (3) = -a, f (1) = ^W = 0, f d(1,7) = f (2)ud(6) - xd(1,7),     f d(0, 4) = f (1), f d(1, t) = f d(1, t + 1)ud(t) - xd(t) + (xd(t)ud(t)ad(1,t + 1) +

+ fd(1,t + 1)) x (2fd(1,t + 1)(t - ud(t)) + 1), fd(0, t) = f d(0, t +1) - (cos (ud(t))ad(0, t +1) x x (f d(0, t +1) cos (ud(t)) + 2(t - ud(t)))) x x (fd(0,t +1)sin (ud(t)) +2) 1;

ct(2) = 1 - a,                   a(1) = a(2) + ad(1, 7) = -a, vd(1, 7) = ct(2) + a - 2 = -1, ad(0,4) = ct(1) + a - 1 = -1, ad(1,t) = (ud(t))2ad(1,t + 1) + a - 2 -

• - ((u2(t)^^d(1,t + 1)x^d(t) + f^d(1,t + 1))²) x

x ((xd(t))V(1,t +1) - 1)Л ad(0, t) = ad(0, t + 1) + a - 1 - (ad(0, t +1) cos (ud(t)))2 x x (ad(0,t +1)cos2 (ud(t)) - fd(0,t + 1) sin (ud(t)) - 2) 1;

Au^d(0,t) = - (f^d(0,t +1)cos (ud(t)) +2(t - ud(t)) +

+ ad(0,t + 1) cos (ud(t))Axd(0, t)) x x (ad(Q,t +1)cos2 (ud(t)) — ^d(Q,t + 1)sin (ud(t)) — 2) 1, Aud(1, t) = (2^d(1, t + 1)(t — ud(t)) + 1 — (xd(t)ud(t)ad(1,t + 1) +

+ ^d(1,t + 1))Axd(1,t)) x ((x^d(t))²a^d(1,t + 1) — 1) ¹.

Решение получено за 2 итерации. Изменение функционала по итерациям представлено в таблице 1.

Таблица 1. Результаты расчетов примера 1

Итерация j	α	I = xd(7) ^ min	|Ij —Ij-11
0		4.366
1	0.2	4.024	0.342
2	0.6	3.947	0.077

При расчетах выбор значения α осуществлялся для обеспечения минимума функционала и находился перебором в диапазоне от 0 до 1 с шагом 0.1. Графики переменных состояния и управления приведены

(а) Состояние

Рисунок 1. Результаты расчетов примера 1

Пример 2. Двухэтапная задача:

1-й этап:

x^d(t + 1) = —2xd(t) + (ud(t))², xd(Q) = 1, t = Q, 1, 2, 3,

1⁰= 1(xd (t))²+ |(ud(t))³;

2-й этап:

x^d(t + 1) = (t — ud(t))2 t = 4, 5, 6, 1¹= 2(x^d(t))2 + ud(t);

I = x^d(7) ^ min .

Как и в предыдущем примере, представим эту систему в виде НДС. Имеем K = 0,1,2, K‘ = 1. Поскольку роль связующей переменной на двух рассматриваемых этапах играет x^d, то в терминах этой переменной легко записать процесс верхнего уровня:

x(0) = xd(0,0), x(1) = xd(0,4), x(2) = xd(1, 7), xd(1,4) = x(1).

Так как множество K^′состоит из одного элемента, то для удобства расчетов, модель может быть дополнена третьим мгновенным этапом, не имеющим протяженности во времени и состоящим лишь в передачи информации об окончании второго этапа на верхний уровень. Тогда

x(3) = x(2) = xd(1,7), K‘ = 1,2, 0(k) = xd(k,t_F), £(k) = x(k).

На обоих этапах процесс нижнего уровня также не зависит от переменных состояния верхнего уровня, тогда

A(0, t) = A(1,t) = 0, Л(0, t) = Л(1,t) = 0.

fd(0,t) = -2xd(t) + (ud(t))2, fd(1,t) = (t - ud(t))2, fXd (0,t) = -2,                  fXd (1,t) = 0, fdd (0,t) = 2ud(t),               fUd (1,t) = -2(t - ud(t));

H^d(0,t) = ^^d(0,t + 1)(-2x^d(t) + (ud(t))²) - |(x^d(t))²-

• — |(ud)3 - |(1 - a)|Ax^d(0)|², 32

HXd (0,t) = -2^^d(0,t +1) - x^d(t),   HXdxd (0,t) = a - 2,

Hdd(0,t) = 2^^d(0,t +1)ud(t) - (ud(t))²,

H^d(0,t) = 2^^d(0,t +1) - 2ud(t),    Hddud(0,t) = 0;

H^d(1,t) = ^^d(1, t + 1)(t - ud)²- |(x^d)²- ud(t) - |(1 - a)|Ax^d(1)|²,

Hdd(1,t) = -x^d(t),         Hddxd(1,t) = a - 2,

Hdd(1,t) = -2^^d(1,t +1)(t - ud(t)) - 1,

Hddduudd (1,t) = 2^^d(1,t + 1), Hdd_ud (1,t) = 0;

^⁽²⁾ = ^⁽³⁾ = ^-a,  ^⁽¹⁾ = ^W = ⁰,

^^d(1, 7) = -x^d(1, 7),     ^^d(0,4) = -2^(1) - x^d(0,4),

^d(1,t) = —xd(t),

^^d(0, t) = -2^d(0, t + 1) — x^d(t) —

• - 2    •   ■   0 + 1)(2^^d(0,t +1) — ud(t))) x

X (^d(0,t + 1) — ud(t)) 1;

ct(2) = 1 — a,                   ff(1) = a(2) + ad(1, 7) = —a, ad(1, 7) = ct(2) + a — 2 = —1, ad(0,4) = ct(1) + a — 2 = —2, ad(1,t) = a — 2, ad(0, t) = 4ad(0, t + 1) + a — 2 — 8 (ud(t)ad(0, t + 1))2 x x (2(ud(t)) V(0, t + 1) + ^d(0, t +1) — ud(t))^1;

Aud(0, t) = —ud(t) (2^d(0, t + 1) — ud(t) — 4ad(0, t + 1)Axd(0, t)) x x (4(ud(t))2CTd(0, t +1) + 2^d(0,t + 1) — 2ud(t)) 1,

Aud(1,t) = (2^d(1,t +1)(t — ud(t)) + 1) x x f Hd,|, t + 1)(t — ud(t))2 + 2^d(1, t + 1))-1.

Решение получено за 8 итераций. Изменение функционала по итерациям представлено в таблице 2.

Таблица 2. Результаты расчетов примера 2

Итерация j	α	I = xd(7) ^ min	|Ij —Ij-1|
0		36
1	0.5	23.702	12.298
2	0.5	13.197	10.505
3	0.5	6.379	6.818
4	0.4	2.199	4.180
5	0.4	0.506	1.693
6	0.4	0.195	0.311
7	0.3	0.117	0.078
8	0.3	0.109	0.008

Графики переменных состояния и управления приведены на рисунках 2а и 2б .

Отметим, что этот пример имеет более сложную структуру. Его решение другим методом приведено в работе [7]. Варьирование параметра альфа позволило получить меньшее значение функционала по сравнению

(а) Состояние

(б) Управление

Рисунок 2. Результаты расчетов примера 2

с результатом работы [7].

Заключение

Таким образом, решенные примеры подтверждают работоспособность построенного метода, который имеет более сложную структуру по сравнению с методом из работы [7] за счет необходимости решения матричных уравнений Риккати для сопряженных переменных. При этом количество итераций незначительно увеличивается, но позволяет получить меньшее значение функционала, чем в [7].

Также дан ответ на вопрос, поставленный в начале статьи: понятие сильного относительного минимума можно использовать для построения метода улучшения для НДС.