Метод синтеза управления движением космического аппарата вокруг центра масс при ограничениях на угловую скорость и угловое ускорение
Автор: Горбулин В.И., Мальцев Г.Н., Ортиков М.Ю., Фадин И.А.
Журнал: Космическая техника и технологии @ktt-energia
Рубрика: Динамика, баллистика, управление движением летательных аппаратов
Статья в выпуске: 4 (47), 2024 года.
Бесплатный доступ
В настоящее время для оперативной передачи информации дистанционного зондирования Земли используются космические системы связи и ретрансляции. Перспективным направлением развития этих систем является использование лазерного канала передачи данных, обладающего большей пропускной способностью. Необходимость удержания узкого луча на космическом аппарате связи и ретрансляции накладывает ограничения на динамику движения космического аппарата дистанционного зондирования Земли вокруг центра масс. В статье предложен метод, позволяющий решить задачу синтеза управления движением космического аппарата вокруг центра масс при ограничениях на угловую скорость и угловое ускорение в классе полиномиальных функций. Получаемое решение является оптимальным по показателю энергозатрат.
Геостационарная орбита, движение вокруг центра масс, космический аппарат, низкая околоземная орбита
Короткий адрес: https://sciup.org/143183664
IDR: 143183664 | УДК: 629.7.076.6:531.381
Текст научной статьи Метод синтеза управления движением космического аппарата вокруг центра масс при ограничениях на угловую скорость и угловое ускорение
Управление движением космического аппарата (КА) вокруг центра масс (ЦМ) является элементом управления движением КА и осуществляется исходя из потребностей выполнения программы полёта и решения КА задач по предназначению [1–4]. При этом особенности выполнения КА целевых задач, с одной стороны, определяют требования к функциональным возможностям бортовой системы управления движением КА вокруг ЦМ, с другой стороны, могут приводить к ограничениям на управление движением КА вокруг ЦМ.
Наиболее сложной во многих случаях оказывается реализация управления движением вокруг ЦМ КА, оснащённых бортовыми оптическими информационными системами различного назначения. Малые размеры углового поля зрения приёмных оптических систем и узкие диаграммы направленности передающих оптических систем приводят к необходимости использования специальных систем их наведения. Для них движение КА вокруг ЦМ является внешним возмущением, которое может приводить к срыву наведения оптической системы. И в то же время управление движением КА необходимо для применения по назначению бортовых оптических информационных систем, жёстко закреплённых в корпусе КА. Так, при дистанционном зондировании Земли необходимо обеспечивать перенацеливание бортовой оптической аппаратуры наблюдения для реализации различных режимов съёмки [5], а при межспутниковой лазерной связи необходимо обеспечивать взаимное наведение бортовых лазерных терминалов [1].
В рассматриваемых случаях, когда применение КА требует изменения ориентации бортовых оптических информационных систем, жёстко закреплённых в корпусе КА, основным ограничением на управление движением КА вокруг ЦМ оказывается ограничение на угловую скорость и угловое ускорение, которые не должны превышать требуемых значений и должны быть минимизированы. В то же время при синтезе управления движением КА вокруг ЦМ эти ограничения, как правило, не выступают в качестве основных. Результаты анализа существующего научнометодического задела в области синтеза управления движением КА вокруг ЦМ с учётом различных ограничений показывают, что к настоящему времени разработаны общие подходы к решению данной задачи, заканчивающиеся построением системы нелинейных дифференциальных уравнений, неразрешимых в общем виде [4], и частные методы синтеза управления движением КА вокруг ЦМ, квази-оптимального по энергии [2] или быстродействию [3]. В настоящей статье на основе общего подхода к решению задачи синтеза управления движением КА вокруг ЦМ получено решение при ограничениях на угловую скорость и угловое ускорение связанной системы координат КА.
Математическая постановка задачи
Дано :
-
• Λ 0 — кватернион ориентации КА относительно абсолютной геоцентрической
экваториальной системы координат (АГЭСК) в начальный момент времени t 0;
-
• Λ b — кватернион ориентации КА относительно АГЭСК в момент времени tb ;
-
• ω 0 — угловая скорость КА в проекциях на оси АГЭСК в момент времени t 0;
-
• ε 0 = 0 — угловое ускорение КА в проекциях на оси АГЭСК в момент времени t 0. Данный параметр можно определить численным дифференцированием измерений угловой скорости или при помощи специализированного измерителя [6];
-
• ω s max — максимально допустимое значение угловой скорости КА;
-
• ε s max — максимально допустимое значение углового ускорения КА;
-
• Mp — область вариации кинетического момента инерционных исполнительных органов;
-
• ω b — угловая скорость КА в момент времени tb ;
-
• ε b — угловое ускорение КА в момент времени tb . Данный параметр определяется в соответствии с целевой задачей, например из условия наведения на наблюдаемый объект;
-
• I 1, I 2, I 3 — главные центральные моменты инерции;
-
• связанные оси КА параллельны главным центральным осям инерции.
Критерий синтеза: минимизация затрат энергии.
Найти:
M(t) = [M1(t), M2(t), M3(t)]T — управление движением КА вокруг ЦМ при переориентации (проекции управляющего момента на оси связанной системы tb координат), fМ(t)dt e Mp V t.
Содержательное описание метода
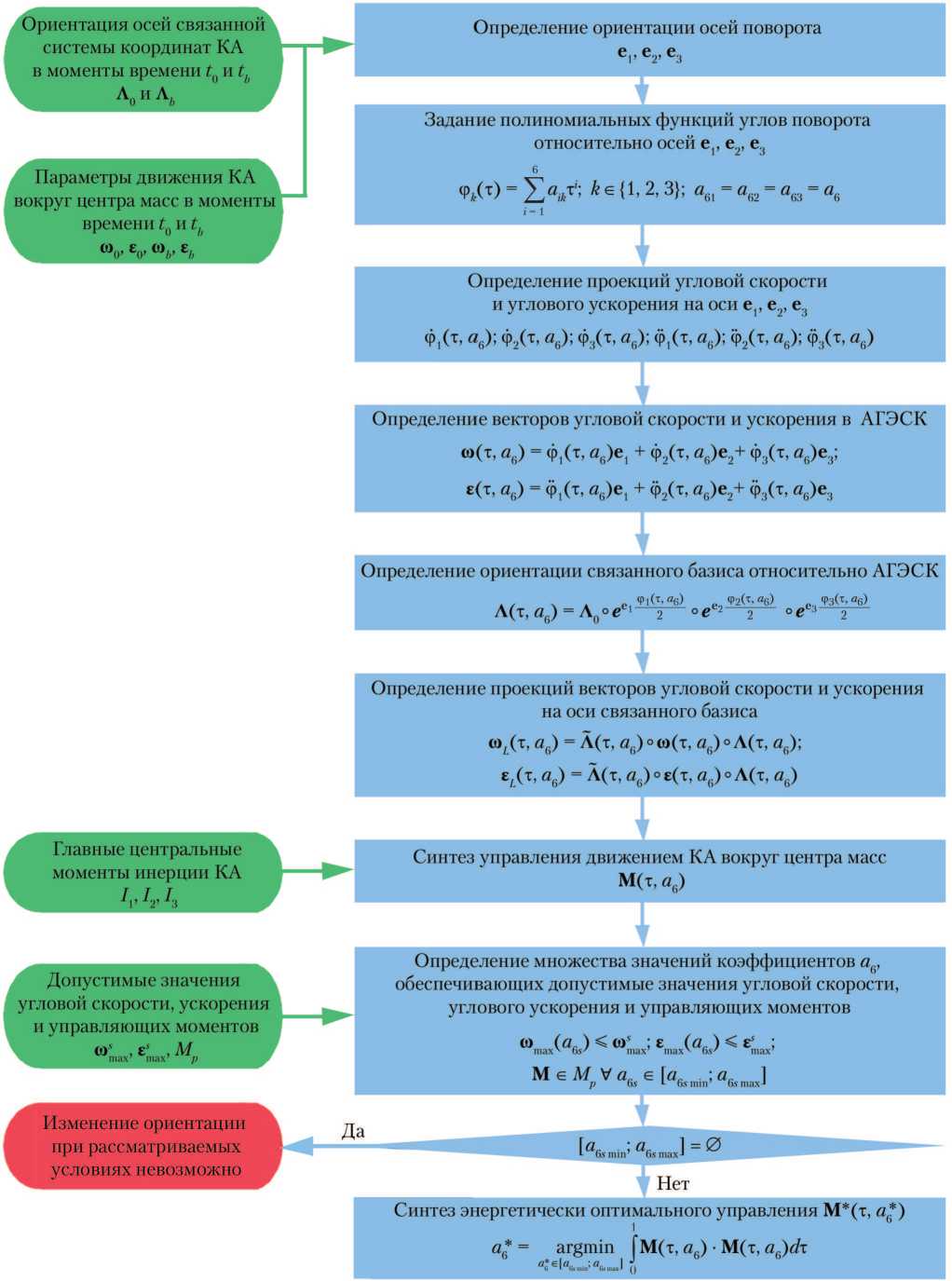
Структурная схема метода синтеза управления движением КА вокруг ЦМ при ограничениях на угловую скорость и угловое ускорение связанной системы координат КА представлена на рис. 1.
Поворот, переводящий КА из ориентации Λ 0 в ориентацию Λ b , представляется в виде трёх элементарных поворотов относительно осей с ортами е 1, е 2, е 3 [2] на углы ϕ 1, ϕ 2, ϕ 3 соответственно.
Параметры движения КА вокруг центра масс в моменты времени t0 и tb «О’ £0> Ч’ Е/,
Главные центральные моменты инерции КА
Ориентация осей связанной системы координат КА в моменты времени 70 и tb Л0ИЛ6
Допустимые значения угловой скорости, ускорения и управляющих моментов со5 , е5 ,М max7 max7 р
( Изменение ориентации при рассматриваемых условиях невозможно
Нет
L ox min7 os max-
Определение множества значений коэффициентов а6, обеспечивающих допустимые значения угловой скорости, углового ускорения и управляющих моментов ю ) < max' 6sz max7 max' bsz max7 M eM Va„ e k . ; 1 p os L os min7 bs maxJ Определение проекций векторов угловой скорости и ускорения на оси связанного базиса «А а6) = Мт, я6)°40(т, а6)°А(т, а6); Е£(т, а6) = Мт, а6) °е(т, а6) °Л(т, а6) Задание полиномиальных функций углов поворота относительно осей ер е„ е3 Ф,(т) = V л.,т"; ^ е {1, 2, 3}; л„. = а_ = а,,., = а,, zZ jik * ’ 7 J7 61 62 63 6 Определение векторов угловой скорости и ускорения в АГЭСК «(т, л6) = ФМ, а6)е, + ф2(т, д6)е2+ ф3(т, а6)е3; £<Л «6) = ф/т а^е, + ф2(т, а6)е2+ ф3(т, л6)е3 Определение проекций угловой скорости и углового ускорения на оси е(, е2, е3 ф/^ «6); Ф2(т, я6); ф3(т, а6); ф/т, л6); ф2(т, л6); ф3(т, л6) Синтез энергетически оптимального управления М*(т, а*) а* = argmin [М(т, л(.) • М(т, aJA Определение ориентации связанного базиса относительно АГЭСК . , . . „ <Р1С«б) „ Ф2С«б) „ ФзС°б) Л(т, л6) = Ло ° е 1 2 °е 2 2 °е 3 2 Определение ориентации осей поворота е1’ е2’ е3 Синтез управления движением КА вокруг центра масс М(т, л6) Рис. 1. Структурная схема метода синтеза управления движением космического аппарата (КА) вокруг центра масс при ограничениях на угловую скорость и угловое ускорение: АГЭСК — абсолютная геоцентрическая экваториальная система координат; a6s— значения a6, соответствующие допустимым значениям угловой скорости, ускорения и управляющих моментов (рисунок создан авторами). Примечание. Остальные обозначения см. в тексте. Углы поворота относительно осей е1, е2, е3 задаются в виде полиномов шестой степени: фк(т)= Е aikтi; i = 1 k ■ {1, 2, 3}; (1) a61 = a62 = a63 = a6, где aik — коэффициенты полинома; т — модифицированное время, t – t0 ' = tb - t0 , т е [0, 1]; t — текущий момент времени, t е [10, tb]; 10 — момент начала разворота. Орт е3 определяется из следующего соотношения: Ф * ф * ~ Л* = cos — + e3 sin — = Л0 ° лb, где Λ* — кватернион поворота в момент времени t = tb; ф* — угол поворота вокруг оси е3 в момент времени t = tb; Λ0 — сопряжённый кватернион в момент начала разворота; знак «°» обозначает кватернионное умножение, тогда Л1(т b) = Л2(т b) = 1;(2) Ф *ф л3(т b) = cos + e3sin T ’ 2) a = eωb – (eωb · e3) · e3. Если |a| > 0,001, то e1 = aa , конец алгоритма. В противном случае выполняется следующий шаг. 3) a = eε0 – (e0ε· e3) · e3. a Если |a| > 0,001, то e1 = a , конец алгоритма. В противном случае выполняется следующий шаг. 4) a = eεb – (eεb · e3) · e3. a Если |a| > 0,001, то e1 = a , иначе поворот вокруг оси е3 — единственный, т. е. Л1(т) ^ 1; Л2(т) ^ 1. Орт оси второго поворота е2 = е3х е1. Проекция угловой скорости на ось ek ю ek(т)= «(т)• ek = фk(т)= a 1 к + 2a2кТ + 3a3кТ2 + 4a4кт3 + 5a5кТ4 + 6a, (4) tb – t0 проекция углового ускорения на ось еk еek(т)= Ф) • ek = фk(т)= 2a2k где Л1(т), Л2(т), Л3(т) кватернионы + 6 a 3 k т + 12 a 4 kт2+ 20 a 5 k т3+ 30 a6т4 (5) (tb – t0)2 . ( ) поворотов относительно осей е1, е2, е3 соответственно, Л1(т) = e61 ^; Л2(т) = e62^2Е; Из соотношения дует, что (4) при t = 0 сле- ФзСО лз(т)= e е 2; тb модифицированное а 1 k Ю0 ek(tb t 0), время в момент времени t = tb. Координаты орта e1 определяются по следующему алгоритму [2]: a 1) если а > 0,001, то e1 = a , конец алгоритма. В противном случае выполняется следующий шаг. где Ю0 ek = юek(0)- Из соотношения дует, что (5) при t = 0 сле- _ S0ek(tb t0) _ „ a 2 k = 2 = 0 гДе е0 ek = еek(0)= 0- Из уравнений (1), (4), (5) с учётом формул (6) и (7) коэффициенты а3k, a4k и а5k выражаются через а6: . Фbk- ФоК(Ть- Т0) - Ф0k(Ч- Т0)2 – a 6 (ф,, - Ф„,)(t, - tn) - Ф„,(t, - tn)2 bk 0k b 0 0k b 0 – 6a . (Фbk Фй)(t, - t.)2 - 30А 0k b 0 6 Таким образом, закон вокруг ЦМ задаётся в мостей фk(т, a6). движения КА виде зависи- Компоненты вектора управления М(т, a6) определяются из следующего соотношения: 11sL 1(Т’ A6) + (13 - 12>®L2(’ A6)®L3(’ A6) М(т, а6) = 12SL2(’ A6) + (11 13)®L 1(^’ A6)®L3(^’ A6) 13sL3(Т, A6) + (12 - 11)®L2(, A6)®L 1(Т, A6) где етLk, sLk — проекции векторов угловой скорости и углового ускорения на оси связанной системы координат соответственно: w L (т, a 6) = Л(т, a 6) ° ю(т, a 6) о Л (т, a 6); £ L (т, a 6) = Л(т, a 6) ° £(т, a 6) ° Л(т, a 6); , . . , „, Ф1(т- a б) „,, Ф2У.А) _ Ф3<3 a б) Л(т, aR) = Л„ ° e12 ° e 2 2 ° e 32 . Проекции векторов угловой скорости и углового ускорения на оси АГЭСК, соответственно, можно выразить в следующем виде: ®(т, a6) = ЕФk(т, a6)ek; k = 1 £(т, a 6) = Е Ф k (т, a 6)e k. k = 1 С помощью соотношений (4)–(9) определяется множество значений А = [a6s min, a6s max] коэффициента а6, на котором выполняются условия ®(т, a 6) < ®max; е(т, a 6) < Smax; > М(т, a6) e Mp, z где ет(т, a 6) Ею2(т, aR)• k , 6 ; k = 1 е(т, a6) Ееl^, a6). к = i Если множество А является пустым, то решение задачи изменения ориентации КА при данных условиях и ограничениях невозможно. Если множество А не является пустым, то осуществляется синтез оптимального по критерию минимума затрат энергии управления М(т, a6*) a6* = argminjM(т, a6) • М(т, a6)dт. (11) a,, e A 0 При решении задачи синтеза управления учитывается определённость углов фbk с точностью до целого числа оборотов: ф*k = фbk+ 2пnk; nkeZ• Выбор значений nk наряду с а6 позволяет уменьшить максимальные величины как угловых скоростей и ускорений на интервале т e [0, 1], так и функционала |М(т, a6) • М(т, a6)dт.
ω ω0 0 ®0;
ω ωb e b ® в ’
ε0
ε
e0 е0;
ε
ε
e b е ь"
a = e“ - (e“ • e3) • e3; a = |a|.
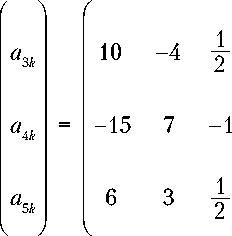

Список литературы Метод синтеза управления движением космического аппарата вокруг центра масс при ограничениях на угловую скорость и угловое ускорение
- Космические системы связи и ретрансляции: монография / Под ред. А.В. Кузовникова. М.: Радиотехника, 2017. 448 с.
- Сомов Е.И. Оптимизация поворотного манёвра и синтез законов гиро-силового наведения космических аппаратов и свободнолетающих роботов // Известия Самарского научного центра РАН. 2007. Т. 9. № 3. С. 824-834. Режим доступа: http://www.ssc.smr.ru/media/journals/izvestia/2007/2007_3_824_834.pdf (дата обращения 05.03.2024). EDN: QAUQLV
- Власов В.А., Горбулин В.И., Зозуля Л.П. Расчёт оптимального по быстродействию перенацеливания оптикоэлектронной аппаратуры космического аппарата дистанционного зондирования Земли // Информация и космос. 2009. № 1. С. 71-81. EDN: KWBTFH
- Молоденков А.В., Сапунков Я.Г. Аналитическое квазиоптимальное решение задачи поворота осесимметричного твёрдого тела с комбинированным функционалом // Известия РАН. Теория и системы управления. 2020. № 3. С. 39-49. EDN: OYYEJS
- Zhuo Wang, Rui Xu. Rapid Search method for a spacecraft attitude maneuver path with multiple constraints // Aerospace Science and Technology. 2021. Vol. 117. URL: 10.1016/jMst.2021.106904 (accessed 05.03.2024). DOI: 10.1016/jMst.2021.106904(accessed05.03.2024)
- Патент RU 2593935 C1, МПК G01P 15/18. Способ измерения линейных ускорений, угловых скоростей и ускорений на борту космического аппарата в условиях, близких к невесомости и устройство для его осуществления / Борисов Б.А., Емельянов Г.А., Лысак А.С., Лукичёв А.С., Медов В.М.; заявитель и патентообладатель - ФГУП ЦНИИмаш. Заявка № 2015115192/28 от 22.04.15. Опубл. 10.08.16. Бюл. № 22.


