Метод скаляризации в задачах распространения поверхностных упругих волн во вращающемся трансверсально-изотропном полупространстве

конструкции при многократном воздействии локальных динамических нагрузок. В [6] дан анализ динамического поведения анизотропных многослойных конструкций и т. д.

Целью настоящей работы является обобщение данного метода на задачи для трансверсально-изотропных сред, вращающихся с постоянной угловой скоростью Ω , а также получение соотношений для описания влияния вращения на параметры поверхностных акустических волн (ПАВ), которые могут использоваться в гироскопах [7–9]. Исходные соотношения. Уравнение движения в перемещениях для монохроматических волн (e’i “t), содержащих массовые силы, по [10, 11] имеет вид:

- to2 р U = VjCijr V( rus)+ F1, где Fi - вектор плотности объемных сил; р — плотность; to — частота.

Для трансверсально-изотропных материалов тензор коэффициентов упругости C ^ijrs может быть разложен на неприводимые части следующим образом [12]:

C irs=Cig ijg rs+C2 (g irg^+gisgr)+C3 [(3 n in j-gij) g-s+(3 n rn s-g rs)g j]+ +C4[(3ninr-gi)gjs+(3njn s-gis)gr+(3n ins-gis)gjr+(3njnr -gF)gir]+ +C5(35 ninjnrns-30 n(in grs))+3 g(ijgrs), где ni — единичный вектор главной оси симметрии;

C = 3 (c|4} + 2C,") ; C2 = 3 (c|4>-c|22^);(2)

c - — (ri4} + гс^22})'   r      (r''4i   X--1221V   c -- H4} c3 = 12 C + 2cg );  c4 = 12 Cg   cg );  c5 = 8 cn ;(3)

c | ^4} = 115 ( 8 C 11 + 3 C 33 + 4 C 13 + 8 C 44 ) ;

C l ²²! = 1 ( - C n + 3 C 12 + 4 C 13 - 4 C 44 ) ;     C^ =    ( - 8 C _n + 6 C 33 + 2 C _n + 4 C 44 ) ;

C?! = 3 (2CH - 6C12 + 4C13 - 4C44);  C{4} = 35 (Cn + C33 - 2C13 - 4C44).(4)

Константы, входящие в коэффициенты разложения (4), являются элементами матрицы упругих постоянных, записанной по свернутому индексу.

Пренебрегая центробежными силами как малой величиной второго порядка, а также учитывая, что О = const , представим массовые силы в виде сил Кориолиса. Тогда вектор плотности объемных сил можно записать следующим образом:

F ^s =- i 2to²p - 8 ^sjk О j u k ,                                               (5)

ω

где Q j — вектор угловой скорости, £ sjk — дискриминантный тензор.

Для квазипродольных и квазипоперечных волн, учитывая работу [3] и принимая во внимание выражение (5), уравнения движения могут быть записаны в виде следующей системы:

• (k) (k)(k)                 (k)          i             1,

V s V sUJ + bl UJ + b 2V J V sus =-7Г" 2to2p-8 Jjs 0 jus;(6)

C44ω

• (k) (k)(k)                 (k)          i 9 1,

VeVa ua + b3 uв + b4VJVe Uj = -—2to2p-8ejs0j us.(7)

C11

Здесь:

( k )      1

b 1 = —

C 44

(         ( к )

®^{2 p} - h ^{2 (} - C 13 + C 33

I

-

2 C 44 )

J

b 2 =7^⁽ C 13 + C 44 ) ;

C 44

^{( k} )      1

b = —

^{3    C} 11

-P - У C 44 I            J

b 4 = 7^ ( C 13 + C 44 );

C 11

( к ) = L, T, индекс L относится к квазипродольным волнам, а индекс T — к квазипоперечным;

( к )

h - проекция волново-

^{( к} )

го вектора g на ось материальной симметрии; индекс J — фиксированный, он соответствует главной оси симметрии материала, в = K,N; фиксированные индексы J, K, N относятся к локальному аффинному реперу eJ, eK, eN, имеющему один инвариантный базисный вектор eJ, когда справедливы уравнения (6) и (7).

Решаемая научная задача заключается в том, чтобы найти аналитическое решение уравнений (6), (7) для трансверсально-изотропного полупространства, вращающегося с постоянной скоростью.

Постановка задачи. Конкретизируем задачу рассмотрением плоских волн, распространяющихся в плоскости, перпендикулярной оси вращения.

Рассмотрим трансверсально-изотропное полупространство, граница которого представляет собой плоскость. Нормаль к границе составляет угол α с направлением оси симметрии полупространства.

Для описания волн в полупространстве введем соответствующую аффинному реперу e J , e_K, e_N Декартову систему координат x J , x K , x N , где ось x J совпадает с осью симметрии материала полупространства, а ось x K лежит в плоскости распространения волн. Вращение полупространства производится вокруг оси x N с угловой скоростью Ω .

( K )                  ( K )

Направление распространения волн определяется волновым вектором g . Вектор g составляет угол θ с осью x J (рис.1).

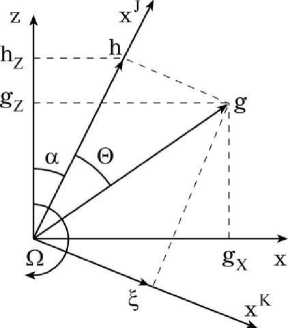
Рис. 1. Расчетная схема плоских волн, распространяющихся в плоскости, перпендикулярной оси вращения

Компоненты перемещений квазипродольных и квазипоперечных волн во вращающемся полупространстве являются решением уравнений движения (6), (7).

Компоненты напряжения могут быть определены из закона Гука:

a ij = C ir V ( _ru_s ) .                                                          (9)

Поле также должно удовлетворять граничным условиям свободной поверхности полупространства.

Механика

Решение задачи.

Объемные волны. Используя метод скаляризации, запишем компоненты перемещений через скалярные потенциалы для квазипродольных волн ф и для квазипоперечных волн W , как это сделано в [3]:

где 5 J — символ Кронекера.

д

U =—⁷ д x i

1 ф + - ^g

(

⁵ J g +

V

д г дxi дxJ

)

W,

Функции ф и W являются решениями уравнений Гельмгольца с собственными значениями

V ( l ) и V ( _т ) — скорости квазипродольных и квазипоперечных волн.

Представим решение уравнений Гельмгольца в виде плоских волн:

.(L) J    -(L) K                    .<т) J   .<т) K i h x i ^ x              i h x i E x ф = фоe e W = Woe    e E ,

( K )  ( K )   ( K )

где h ² +^ ² = g ² .

Используя (10), из выражений (6) и (7) соответственно получим:

P 11 Ф + P 12 W = 0;  P 21 Ф + P 22 W = 0,

где:

( L ) ( к )            ( K )      ⁽ L^L )         _-

P 11 = ^ih [ ^— g ^{2 ( 1 + b} 2 ) ⁺ b ] + — ²® 2P— ^; C 44

ω

( т )

_£ ² (K)  ⁽ K )

P 12 =^ K ) ^{( b}1 ^{— g} ) ⁺

g

( т )( т )

i ^ h . 2 ^ I K T ^{2 и Р} _И ^;

^С 44

g

(к)       , g = И V(к);

(L) (K)  (L)    (L)                 Q p21 = i^ (b3 — ^2 — b4h2) — -h-2и2р- ;

С_п     и

^в 22

(т)(т) м й2Е (т) (K) ' (^ 2 — b 3

—

—

( т )

b 4 5 ² ) +

( т )

g

^ ²_? 2 - -----r—_x 2и p . C_n ^{( K} )     и

i

g

Приравнивая к нулю определитель системы уравнений (12), найдем соотношение для определения

( к )

g . В ре-

зультате получившееся уравнение отличается от аналогичного в [3, 11] наличием слагаемых, учитывающих вращение среды. Если вращение отсутствует (— = 0), то это соотношение совпадает с соответствующим уравнением для одно- осных кристаллов [11].

Из выражения (12) следует соотношение В= ^ф Ду =- в;₂/Р_т] = - Р₂₂/в₂р используя которое запишем формулу (10) для определения перемещений через скалярные потенциалы в форме, аналогичной [3]:

f^{( L} ) д    ^{( L} )   д J )

U; = I D    + D₇ —г 5, ф +

¹ V ¹ д x i      ² д x J  ¹ 7

( L )Г( L )   ( L )

( L )

D = 1

—

1 (т)    д2       (т) J т D1    x + g 5i

W ;

V g

( L )( L )

( ^L ) ( l )    ( ^L )

h2 b1— g2(1 + b2) + i7^2®2p~ J С44      и wn —;

^{L L ( L )}c L ) i       о

^² (b — g ² ) + i^ h -^2rn²p^-

^C 44      И

( L )

D 2 =

( L ) ( L )   ( L )   ( L )

i 2 ( 2² — b 3 — 2 2 b 4 )

I—

( L )

1  2 2, 2 □

2to p —

C ₄₄ ⁽ L )        to

44 h

(L)(L) (L1      (L1     (L)     2 Q i2 (b3 — 22—b4 h2) — -h-2to2p-

C 11 ^to

;

( t )

D 1 = 1 +

( T )

12         ( T )       ₁ ( T )

i I) (b — g ² ) —    I ^V| p'’

^{( 1} )              C₄₄           m

h

( t )Г   ( t )

ih

—

T"

.

Компоненты тензора напряжений находятся из закона Гука:

<3 =

^U j

+

g ^{2 (} 1 + b ₂ ^{) +} b 1 + -|- 2to²p° C 44       to

(L)        (L)   ,   ,    (L )1      , d 15 ij + d 2 5 J 5 J + d 3 2 5 J

/

V

J

i

"( t )      5     ( t ) , , 5

d 5,-, -^7 + d ₂ 5 J 5 J -^d₇ +

^{1 j} 5 x^{J 2} i ^j 5 x^J

где в соответствии с [3] имеем:

( l )       ^{( L} 2       ⁽ L ) f ( l ) ( l )

d 1 = — g a i + h a 3 I D i + D 2

;

( L )

( L )

( L )    ( L )

d ₃ = 2 a ₂ D ₂ + 2 a ₄ I 2 D 1 + D ₂ I ;

^{( t} )       ^{( t} /     ^{( t} ))      f ^{( t} )  ^{( T} ) ^{( T} ) ⁽ T ))

d 1 = a 1 g 11 — D 1 1 + a 3 g — h ² g ¹ D 1

V

5 ²

5 x^j d x^J

+ 5'

■ j 5

A

^j 5 x i 5 x J ₇

d

5 J —- + 5' 5 x j

( L ) d 2 =

( L )

—

;

( t )         ( t )       f ( t ) ^{( t} 2 ^{( T} ) ( t )

d 3 = 2 a ₂ g + 2 a 4 g — 2 h ² g ¹ D 1

;

V

^a 1 = ^C12 ; ^a 2 = 2 ^(C 11 ^{— C} 12 ) ;

^a 4 = 2 ^(C 11

—

C 12 ) + C 44 ;

5    ⁽ l )  d ²

^”7 ^{+ d} 4~^~ d x^J     d x d xj

J ⁵ )   ⁽ T )

---7 I ^{+ d} 4

5 x 7     5 x 5 x j 5 x^J

( L )

g 2 a

( L )

Ф +

W ,

^{( L} ₂ ⁾f       ( l )        ( l )       ( l )

— h I 2 a 4 D 2 + a 5 D 2 + a 5 D 1

d ₄ = 2 a ₂ D 1 ;

;

f( t )  ⁽ T H ^t )( t )

(T)      (T )f    (t )^        (t )     [_ d2 = a3 g| 1 — D1 | + 2a4 g + a5 g — h2 g1 D1

( T )

( t ) ^{( t} )

d 4 = 2 a 2 D i g

;

^a 3 = ^{— C} 12 ^{+ C} 13^;

Л

;

V

a₅ = C 11 + C 33 — 2 (C 13 + 2 C 44 ) .

Таким образом, формулы (14) и (16) описывают тензорные поля перемещений и напряжений через скалярные потенциалы и могут использоваться при расчете параметров упругих волн, находящихся в поле сил Кориолиса. Заметим, что форма соотношений (14) и (16) совпадает с формулами для полей, записанных через скалярные потенциалы в [3]. Отличие заключается в значении коэффициентов (15), в которых есть слагаемые, учитывающие вращение.

Поверхностные волны. С целью удовлетворения граничным условиям для удобства введем связанную с границей декартову систему координат x, y, z , которая образуется поворотом системы координат x J , x K , x N путем против часовой стрелки вокруг оси x N на угол α (см. рис. 1). В этом случае уравнения преобразования имеют вид:

z = — x^K sin a + x^J cos a;                         x^K = xcos a — zsin a ;

x = x^K cos a + x^J sin a;                            x^J = xsin a + zcos a ;

y = x N ;                                          x^N = y .                                 (19)

При этом ось z совпадает с нормалью к границе, а оси x, y направлены параллельно ей.

Компоненты полей в системе координат x, y, z могут быть выражены через компоненты в системе координат x J , x K , x N следующим образом [13]:

dxJ     dxK uz = -^uj+ -^uK; dz       dz

ux

5 x ^J

d x ^K

Механика

5 x

J

+--u

K ;

_ 5 x^J 5 x m      5 x^K 5 xm     ,

^ zz = -    -  ^ Jm ⁺ -   -  ^ Km ^;

o z  d z        d z   о z

_ 5 x^J 5 x m      5 x K 5 x m

^ zx = -.       ^ Jm +          ^ Km- dz  dx       dz  dx

Зависимости проекций h , £, волнового вектора g на оси координат x J , x K , x^N и проекции этого вектора на оси

координат x, y, z выглядят так:

h =

cos θ

cos θ

sin ( a + 9 ) g x    cos ( a + 9 ) gz ’

5 =

sin θ

sin θ

sin ( a + 9 ) g x    cos ( a + 9 ) gz ’

g 2 = h ² + ^ ² = g_z ² + g x ² .

Используя выражения (19)–(21) из соотношений (14), (16) и (20), после несложных преобразований получим

формулы для описания полей в системе координат x, y, z :

( t )

.(L ’"(L ’ cos 9 cos а (L )7     (T)"      n(T ’     cos а 7 g uz = igz\D1+          D2 |ф+igz\— cos9D1+          krW;

V      cos ( а + 9 )    J       V             cos ( а + 9 ) 7⁽ T ’

(.1

^{( L} )| cos 9 cos а\⁽ L ’ ( L ’7 sin 9 cos а^ ^ ’)- g ^(T )i u x = igz\            l D - ⁺ D 2 | ⁺            D - ф ⁺ i -ay g z I

| cos ( а + 9 )              cos ( а + 9 )    J     ⁽ T ’

—

sin ( а + 9 ) cos 9 ( T ’      sin а 7

—v—   — D1 +-- 7 ---z | W ;

cos ( а + 9 )        cos ( а + 9 ) J

^σ zz

= S cos a

⁽ L ’ ⁽ L ’ "( L ’ ( L )7 cos ² 9 ⁽ L 2 ^d 1 ^{+ d} 2 ^— \ ^d 3 ^{+ d} 4 ¹ “7 ^g z

V       J cos ² ( a + 9 )

\ 1 ^{( L} ) ^{( L} ))     sin 29     ⁽ L 2

+ sin 2al d ₃ + d ₄ |-----—,-----г g 2 +

V 2 ^{3   4} J 2 cos ² ( a + 9 ) z

\( L )  ( L )

+ sin² а d 1 — d

sin ² 9

( L Л1-

V

4 cos ² ( а + 9 )

g z ²

^Ф 7j

( t )

g ₂

— cos а ^

cos 9 cos ( а + 9 )

( T )(( T )  ( T )    ( T )    ( T )

g z ^d 1 ^{+ d} 2 ^{+ d} 3 V

— d

cos ² 9

⁴ cos ² ( а + 9 )

^(T )) g

—

— sin 2 а

sin 9 g z

/

cos ( а + 9 ) 2

1 ( t )   ( t )

- d 3 — ’

d

cos ² 9

⁴ cos ² ( а + 9 )

^{( T} ) ) ^g z

( t )

cos 9 g + sin а---z---z cos (а + 9)

" ( T ) ( T ) ^d 1 ^— d 4

V

sin ² 9     ^T2

cos ² ( а + 9) ^ z ₇

W ;

σ zx

f 1           ( L )

= < — sin 2а d₂

1 ^{2           2}

( L )

( L )

—

d 3 + d 4

cos2θ cos 2 (a + 9)

( L ₂)   ( L )

^g z ^{+ d} 4

cos

sin ² θ

² ( а + б )

^{( L} )" g 2

(         ₂ f 1 ( L ) ( L ’7

— ( 1 — 2 sin ²al — d 3 + d ₄ I x

sin 29

x"—

2 cos ² ( а + 9 )

( L ’b g^T ’f 1

g z ^{2 :ф}    _: \^{sin 2а}

^   ²

cos 9 cos ( а + 9 )

( T )\ ( T )    ( T )    ( T )

g z ^d 2 ^{+ d} 3

V

^— d

cos 29

⁴ cos ² ( а + 9 )

^{( T} ’7 g

+

+ ( 1 — 2 sin ² a

\ sin 9    ^{( T} ’"

^; ’ gz ?

cos ( a + 9 )    \ 2

1 ( T ) ( T )

- d 3 — d 4   2

cos

cos

2 _θ

( а + 9 )

^(T ’) g z

W .

^{( L} )      ^{( L} )      ___ ( T )      ( T )

Здесь ф = ф о e^{l g}zz e^lg x^x ; W = W ₀ e^{l g}z^z e^lg,x

( l ) g_x

.

Таким образом, найдены выражения для компонентов полей, которые входят в граничные условия.

Так как в полупространстве существуют падающие и отраженные волны, а в силу закона Снеллиуса

⁽ T )                     _

= g x = g , функции ф и W могут быть записаны в виде:

(       ( L )

Ф =\ ф ⁺ e^ig z ^z

—

+Ф e

( L ) A

:^—ig z ^z e^V ¹ ,

_  \     ( T )

W = 1 W ⁺ e i ^g z z + W e

( T ) A

■^—ig z ^z I e ig x x e ^{— i m} t

.

Здесь ф±, W ± — амплитуды, подлежащие определению из граничных условий.

Для удобства дальнейшего изложения представим компоненты перемещений ui и напряжений σij, входящие в граничные условия, в виде вектор-столбца:

B = ( u_z,u x , с zz , с zx ) ^T = ( u, c T .

Для определения этих компонентов запишем следующее матричное соотношение:

B = CF V ,

где:

C = ( ^C 1 1 )   ^C 1 2 )1 ; F J ^F *    0 1 ; T = ( ^T ‘ 1 ;

I C ( 3 )   ^C ( 4 ) J’         ( 0 F - J’         ( T ^— J’

F *

e№ z

. T )      ^;

e ig z z

F ^—

(    ( L )               1

e "^igzZ 0

0     e-z ;

V *

ф *

W *

V —

ф

( W ^—

^C ( 1 ) =

1 C ⁽¹"

I ^C ( 21 )

C ( 12 )

C ( 22 )

c (И C ⁽³¹⁾ C ⁽³²⁾1

I C (41) C (42) J g x   — itot

Здесь опущены фазовый и временной множители e ^x , e

Блоки C (₂) и C ( 4 ) совпадают соответственно с C ( 1 ) и C (₃), если у элементов главной диагонали матрицы C ( 1 )

и побочной диагонали матрицы C (₃) изменить знаки на противоположные.

Элементы С (у) матрицы C определяются из формул (22)-(25). Они представляют собой выражения, которые являются множителями, стоящими в формулах (22)-(25) перед функциями ф и W . Например, элемент С ( 11 ) — это множитель перед ф в формуле (22), элемент С (₁₂ ) — множитель перед W в этой формуле, элемент С ( ₂₁ ) — множитель перед ф в формуле (23) и т. д.

Зная значения элементов матрицы С, можно для различных материалов определить параметры волны в зависимости от вращения Q полупространства, а также от углов а и 9 .

Граничные условия в данных обозначениях запишутся так:

• 1    u 1

B = I    I , при z = 0.                                                   (29)

Компоненты вектор-столбца V представляют собой амплитуды падающих и отраженных полей в полупро- странстве. Если представить падающее поле в виде продольной волны с единичной амплитудой, то отраженное поле будет определяться коэффициентами отражения Гфф, ГфЖ и вектор-столбец V = (1, 0, Гфф, ГфW) T. При падающей поперечной волне единичной амплитуды V =(0, 1, rWф,rWW)T. Подставляя эти значения V в соотношение (28) и учитывая, что напряжение на свободной поверхности равно 0 (29), можно найти формулы для компонентов Г . Совокупность этих формул запишем в виде выражения для матрицы Г следующим образом:

( г г= ^Г ф W

r w ф '     C — 1 C . = L 1 C ( 42 ) C ( 31 ) * C ( 32 ) C ( 41 )        2 C ( 42 ) C ( 32 )     \                  (30) I        ( 4 ) ( 3 )                                                                            I ;                       () r WW J                  A 1 (      2C ( 41 ) C ( 31 )         C ( 41 ) C ( 32 ) * C ( 31 ) C ( 42) J ^ 1 = C ( 33 ) C ( 44 ) — C ( 43 ) C ( 34 ) .                                                   (31)

Механика

Для определения скорости распространения ПАВ вдоль свободной границы достаточно приравнять к нулю определитель A 1 (31) и решить получившееся уравнение относительно g x = ю/ V R , где V R - скорость ПАВ.

Компоненты перемещений для волн, распространяющихся в приграничном слое, могут быть найдены из выражений:

(                  (L)( i g7 z                 ig7 z   ig-Л -- iюt uz = A01 C(11) C(42)e     - C(12) C(41) e     Ie e ;

Г                  (L)(

Ux = A о I C(21) C(42) eigzz - C(22) C(41) e8*1 Ieigxe-i" t.(32)

Для поверхностных волн, когда они убывают при удалении от границы, величины gz являются мнимыми (L)     (L) (T)( gz = iaz, gz = iaz, и вещественные значения uz и ux описывают траекторию частиц, участвующих в переносе ПАВ.

Таким образом, полученные соотношения позволяют исследовать влияние вращения на параметры ПАВ в трансверсально-изотропном полупространстве. Для этого достаточно найти коэффициенты C ij из выражений (22)– ( к )

(25), где g определяются из (12) при А = 0. Далее по формуле (31) при А1 = 0 вычислить фазовую скорость и, сле- довательно, частоту ПАВ. Затем, используя (32), можно определить изменение амплитуды колебаний частиц, участвующих в переносе ПАВ, а также форму эллиптической траектории движения частиц.

Изотропные среды. В качестве примера рассмотрим изменение параметров ПАВ в изотропном вращающемся полу- пространстве.

В изотропном случае имеем:

С 11 = С зз = X + 2ц;    С 13 =- С 12 = X ;    С 44 = ц ;

а 1 = X ;          а ₂ = ц;    а₃ = a ₄ = а₅ = 0;

( L )            ₂            ( L )                  ( L )

d 1 =- Xq х ²; d ₂ = 0; d 3 = 2p R 2 ;

( t )

d ₂ = 0;

^{( L} )      ( a      ( t )           *

d 4 = 2 ц ( 1 — R 3 ) ;    d 1 = - XqR 1 ;

( t )

^d 3 = 2цх ;

⁽ T )

d ₄ = 2ц- ( 1 + R ) . ^χ

( ^L )            * ( L )       » ( T )           .

Здесь D 1 = 1 + R ₃ ; D ₂ = R ₂ ; D 1 = 1 + R 1 ; R 1

-2

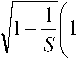
- q

Ω

ω

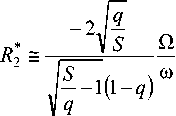
R * =

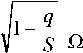
V ⁽ 1 ^- q ) ^ю

_w                     „      Г П A²

Малой величиной второго порядка I — I l ю ;

пренебрегли.

(,K)   (L)  (T)   Ю2р , X + ц b1 = b1 = b1 =      ; b 2 =       ;

μμ

⁽ K )_ Ю 2 Р - h2Ц . ,  _ X + ц .

³ " X + 2ц ;  ⁴ = X + 2ц ;

λ, μ — упругие константы Ламе.

Элементы матрицы C имеют вид:

C ( 11 ) = i ^{( r} 2 ^{- R} 3 )X V q ^- 5 + i X V q ^- 5 ^;

C ( 12 ) = - > k 5 - x ( 1 - 5 ) R * ] ;

C ( 21 ) ^- - i^R + i ^ s ; C ( 22 ) - i (xV1 ^- S + xV1 ^- SR i ^{) ;}

C ( 31 ) - -MX² ( 1 - 2 S ) - 2цх ² ( q - S X R * - R * ) ;

C(32) - --4 fMX2f1 - 2SJЛ-SR* - 2mx2SЛ-S V S (   (q JJ

C ( 41 ) - - X ² Jq-S Ss 2M f 1 + 2 R ** J + X ² V q - S V S 2p R * ;

C(42)--X2(1 -S)2mR* + X22pfS -2J.(35)

„          K2   „ g 2 to to        to          I X + 2ц

Здесь q -—у ; S - —x ; k - —; x - — ; g x - —; Vi -J-----; v t -    ; v l — скорость продольных волн; v t —ско-

χ 2 χ2      vl      vt        vR             ρρ рость поперечных волн; vR — скорость ПАВ.

Скорость распространения ПАВ определяется при А1 - 0 из уравнения (31), которое в явном виде выглядит следующим образом:

[ ( 1 - 2 S ) ² + 4 S V q - S Л- S ] + 2

( 1 - 2 S )( 1 - S ) - V q - S ЛЛ ? 1 ¹ - 2 S I q .

R * +

+ 2 [ ( 1 - 2 S X q - S ) + S Л- S_vq SR* - 2 [ ( 1 - 2 S X q - S ) + 2 S Л- S_vq SR* - 0,

где необходимо брать вещественные корни.

Это уравнение отличается от известного [14] наличием слагаемых, учитывающих вращение полупространства. Определив из уравнения (36) величину S при заданных q и Ω , можно использовать формулы (35) для нахож- дения компонентов поля (27).

Для волн, распространяющихся в приграничном слое, эти компоненты могут быть записаны в виде:

(L)( uz - C(П)ф++ C(12)^+eigzz;

(L)(

Ux - CИФ+eigzz + C(22W+eigzz;(37)

(L)( azz - CФ +eigz + C(32W+eigzz ;

(L)( azx - C(41)Ф+eigzz + C(42W+eigzz.(38)

Найдем амплитуды потенциалов ф ⁺ и W ⁺ . Для этого предположим, что источники в виде давления расположены на границе. Тогда, используя граничные условия, можно решить систему уравнений (38) и, подставив решение в (37), получим выражение для компонентов перемещений. Восстанавливая множитель e i ^ю t e ig x x , имеем:

(                  ( l )                        ( t ) А g7 z    z-ч             i g7 z    -itot igvx uz - A0 IC(11)C(42)e     - C(12) C(41)e      Iee

Механика

f                       ,( L )                              ,( T ) A

^ i g? z                  i g₇ z - i to t ^ig_Yx

I C(21)C(42)e z - C(22)C(41)e z Iee

Для поверхностных волн, когда волны убывают при удалении от границы, величины g z являются мнимыми

(L)     (L) (T)( gz - i a, gz - i а и вещественные значения uz и ux описывают траекторию частиц, участвующих в переносе ПАВ.

Движение частиц вблизи поверхности может быть найдено из (39) при z = 0 и после подстановки элементов матрицы C ( ij ) из (35) определяется следующими формулами:

u z = A 2 V s - q [ - 1 +⁽ s - 1 ) R * + ^R* ] sin ⁽ g x x - ® t ) ;

ux

= A W [o , 5 - s +

s - 0 , 5

-

*

s -1 V s - q R *

+

+ 0 , 5V s -1V s - qR * ] cos ( g x x - № t ) .

Здесь s находится из уравнения (36).

Из этих формул видно, что траектория смещения частиц в поверхностной волне представляет собой эллипс, оси которого зависят от скорости вращения различным образом.

Численное моделирование и анализ его результатов. В качестве иллюстрации на рис. 2 приведен график, со- v2

ответствующий зависимости скорости распространения ПАВ S = 2 от скорости вращения полупространства vR2

Ω w = при q = 0,33 .

ω

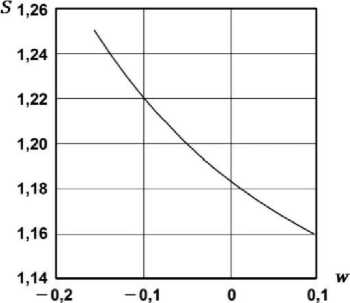
Рис. 2. График зависимости скорости распространения ПАВ от скорости вращения полупространства

Как видно из данного графика, фазовая скорость увеличивается или уменьшается в зависимости от направления вращения Ω полупространства. При малом вращении эта зависимость имеет почти линейный характер.

На рис. 3 приведены траектории движения частиц на поверхности при w = 0 , w = 0 , 01 , w = 0 , 02 и w = 0 , 08 соответственно для q = 0 , 33 .

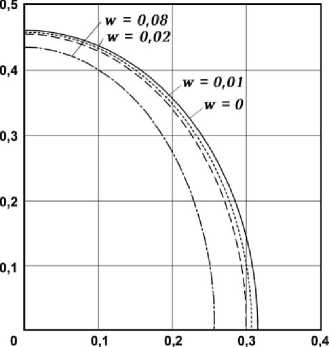
Рис. 3. Траектории движения частиц на поверхности при различных скоростях вращения полупространства

Как видно, траектория движения частиц вблизи поверхности изменяется при вращении полупространства. Причем малая ось эллипса изменяется в большей степени, чем большая.

Вывод. Таким образом, с помощью метода скаляризации найдено аналитическое решение задачи исследования параметров ПАВ при вращении трансверсально-изотропного полупространства. Кроме того, приведены соотношения для расчета фазовой скорости (и, следовательно, частоты ПАВ), а также амплитуды и формы движения частиц, участвующих в переносе ПАВ. Все эти факторы могут использоваться при конструировании гироскопов на акустических волнах.