Метод согласованной идентификации в задаче определения соответственных точек на изображениях

Задача трансформации изображений, заключающаяся в формировании строк соответственных точек на изображениях, является одной из распространённых и востребованных задач обработки изображений. Эта проблема является актуальной в задачах построения цифровой модели рельефа (ЦМР), нахождения ключевых точек для формирования HOG-дескрипторов в задаче распознавания и др.

Для построения преобразований используется так называемая фундаментальная матрица [1], [2], формируемая по небольшому числу заданных соответственных точек. Для нахождения фундаментальной матрицы обычно используется алгоритм RANSAC [3], [4]. При использовании этого алгоритма ищется единственный набор данных, наилучшим образом соответствующих модели в заданном смысле.

Популярность этого алгоритма связана с его высокой устойчивостью к грубым ошибкам типа сбоев. На сегодняшний день он признаётся одним из наиболее эффективных в условиях сильного зашумления исходных данных. Тем не менее построение модели лишь на одном наборе данных иногда приводит к грубым ошибкам в определении модели.

В настоящей работе предлагается новый подход к определению параметров моделей в условиях сильной зашумлённости, основанный на согласованной идентификации [5]. Идея метода состоит в определении модели по некоторому подмножеству наиболее согласованных данных. В работе рассматривается применение этого метода к задаче определения фундаментальной матрицы. Приводятся результаты исследования эффективности применения этого метода по сравнению с алгоритмом RANSAC.

1. Формулировка задачи построения фундаментальной матрицы

Рассмотрим общую задачу восстановления сцены по двум видам. Эта задача решается в рамках эпиполярной геометрии - проективной геометрии между двумя изображениями.

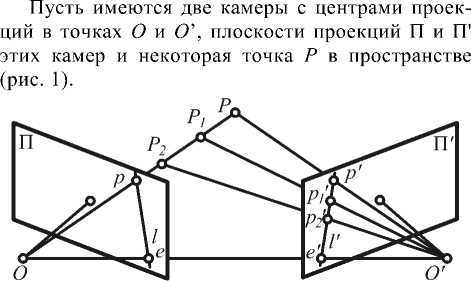
Рис. 1. Модель эпиполярной геометрии

Точки е и е’, пересечения линии ОО’ с плоскостями П и П’, называются эпиполюсами, а линии / и / ’ пересечения плоскости ОО ’Р с плоскостями П и П’ - эпиполярными линиями для точки Р. Точки на двух изображениях, которые являются проекциями одной и той же точки сцены, называются соответственными.

Соответственные точки на двух проекциях связаны фундаментальной Зх3-матрицей F, в частности, для соответственных точек, координаты которых заданы 3 х 1-векторами х, х':

X =

и

3'

и' у'

выполняется условие

(x')7’Fx = 0,

^и

где F = Р_гх

LEi

^12

f22

^32

Fa

F^_

(D

Для одной пары заданных соответственных точек соотношение (1) является линейным однородным уравнением относительно коэффициентов

F_kj, ij = \,3 фундаментальной матрицы.

Для N пар (W>8) соответственных точек, полагая во всех соотношениях F₃₃ = 1, можно записать систему N неоднородных линейных уравнений [6] вида

У = Хс + §,                                  (2)

где с - вектор искомых параметров, составленный из коэффициентов фундаментальной матрицы F:

c = [q, с₂, •••, c₈f =

= [Г1 ^12 ^13 ^21 ^22 ^23 ^31 ^32 ] ’ a Nx 8 -матрица X и Nx 8 -векторы у и § определяются как

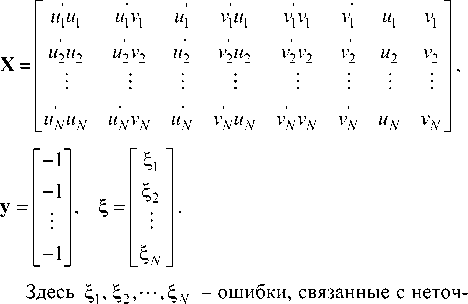
ным заданием координат соответственных точек.

Оценку с вектора с, составленного из элементов фундаментальной матрицы, можно получить применяя метод наименьших квадратов (МНК). Поскольку МНК чувствителен к грубым ошибкам, которые могут иметь место при задании соответственных точек, обычно применяют алгоритм RANSAC.

Как уже отмечалось выше, алгоритм RANSAC, обладая несомненно высокой точностью, в ряде случаев оказывается недостаточно надёжным, т.к. для построения модели используется единственный набор данных. В настоящей работе исследуется возможность повышения надёжности оценок за счёт применения метода согласованной идентификации как альтернативы RANSAC.

• 2.    Описание алгоритмов

Приведём краткое описание алгоритмов решения описанной задачи с использованием методов RANSAC [3], [4] и согласованной идентификации [5].

Идея метода RANSAC (RANdom SAmple Consensus) состоит в том, что по имеющимся данным последовательно строятся модели («гипотезы»). При этом все исходные данные разделяют на два типа: удовлетворяющие модели, «не-выбросы», или «ин-лаеры» (inlier), и ложные точки, искажённые (возможно аномальными) ошибками, - случайные включения в исходные данные, «выбросы», или «аутлае-ры» (outlier).

Качество гипотезы определяется количеством элементов исходных данных, ей удовлетворяющих. Степень согласия гипотезы и исходных данных вычисляется следующим образом:

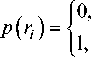
п>т,

где г, (с_к ) - невязка, вычисленная в i -й строке матрицы X, для оценки с_к, удовлетворяющей некоторой гиперплоскости, а Г - фиксированный порог, задаваемый из некоторых общих соображений или свойств исходных данных. Принимается та гипотеза, для которой величина Р^с^ принимает мини-мальноезначение.

В методе согласованной идентификации из исходной системы (2) формируется множество так называемых подсистем нижнего уровня:

у, =Х_А+^Д=1,2,..„ (3)

где

Ук =G.y, X_k=G_kX, ^=G,y,

G - диагональная матрица, составленная из нулей и единиц: rankG_k = dimG_t =8 (рассматривается простейший случай согласованной идентификации, когда подсистемы нижнего уровня задаются квадратными матрицами 8x8). Ясно, что при этом число подсистем нижнего уровня не превышает C_N .

Вычисляя для каждой из построенных таким образом подсистем МНК-оценку с^СХ^ХГ'х^у,             (4)

получаем множество Е всех возможных оценок на подсистемах нижнего уровня.

Аналогичным образом (из нулей и единиц) строится множество диагональных Р^Р-матриц H_z:

гаиШ,=Л (8<Р<А), / = 1, L, L

С использованием этих матриц формируются так называемые подсистемы верхнего уровня:

y/=X_zc_z+^_z,                            (5)

где xz =Н,Х, yz =Hzy, ^z =Hzy, l = \,L.

Каждой подсистеме верхнего уровня принадлежит некоторое множество подсистем нижнего уровня и, соответственно, множество 0Z оценок (4):

0,={ctes, |s|<4],|oz|

Для характеристики множеств 0Z вводится критерий взаимной близости оценок:

^ [©/]=!

0=1

где К = С^%_Р.

Множество 0,, для которого W (0Z) принимает минимальное значение, называют наиболее согласованным. Задача заключается в отыскании этого мно- жества и построении на нём точечной оценки. По существу, задача сводится к отысканию индекса / :

^(Z) = min^(0/).

• 3.    Результаты экспериментальных исследований

Сравнительные экспериментальные исследования метода согласованной идентификации и алгоритма RAN SAC проводились с целью сопоставления их точности в одинаковых условиях функционирования. Эксперименты проводились на наборах данных, которые моделировались следующим образом.

Строились различные системы вида (2) с числом оцениваемых параметров М, равным 8, и числом наблюдений N, равным, соответственно, 12 и 16. Компоненты вектора параметров с задавались в виде равномерно распределённых случайных чисел (РРСЧ) в диапазоне от 1 до 10. Элементы матрицы X вычислялись в соответствии с (2) по координатам соответственных точек, которые моделировались как случайные последовательности с заданными дисперсиями.

Компоненты вектора ошибок формировались таким образом, чтобы для нормальных ошибок отношение сигнал/шум находилось в пределах 40-60 дБ. Для аномальных ошибок отношение сигнал/шум задавалось в пределах 0-10 дБ.

В большинстве известных модельных примеров, используемых в публикациях, посвящённых исследованию эффективности метода RANSAC, число наблюдений N значительно (на 2-3 порядка) превышает число оцениваемых параметров М. Если при этом интенсивность помех находится в разумных пределах, традиционные статистические схемы обработки дают хороший результат. Поэтому при большом числе степеней свободы цель большинства работ состоит в том, чтобы показать преимущества метода RANSAC в условиях, когда число аномальных ошибок достигает 80-90% от общего числа наблюдений.

В рассматриваемой задаче число наблюдений N обычно ненамного превышает М(не более, чем в 2-3 раза). В данном случае статистические схемы обработки принципиально непригодны. В настоящей работе исследуется именно этот случай. При этом интенсивность аномальных ошибок задавалась более реалистичной - 50-60% от числа степеней свободы N-М полученной системы.

Для сравнительной оценки точности и надёжности алгоритмов используются следующие показатели: идентификация считается верной, если отношение нормы вектора погрешности к норме вектора параметров не превосходит 0,3.

На рис. 2 приведены графики зависимости средних значений погрешности верных идентификаций от числа аномальных ошибок для различных значений числа оцениваемых параметров (светлый - для метода RANSAC, тёмный - для метода согласованной идентификации). На рис. 3 для тех же значений числа оцениваемых параметров приведены графики зависимости числа ложных идентификаций на 100 экспериментов от числа аномальных ошибок. Нетрудно заметить, что на всех реализациях метод согласованной идентификации показывает лучшие результаты как по надёжности, так и по точности.

Рис. 2. Средняя погрешность верных идентификации: N=12, М=8 (a); N=16, М=8 (б)

Рис. 3. Число ложных идентификаций на 100 экспериментов: N=12, М=8 (a): N=16, М=8 (б)

На рис. 4 приведён пример нахождения соответственных точек. Показанные на рисунке эпиполярные линии определены с использованием фунда-

ментальной матрицы, которая оценивалась методом согласованной идентификации. Соответственные точки находятся на эпиполярных линях любым известным методом, например, с использованием нормированного коэффициента корреляции.

Рис. 4. Пример нахождения соответственных точек на эпиполярных линиях

Применение метода согласованной идентификации позволяет существенно повысить точность и надёжность определения коэффициентов фундаментальной матрицы, что в конечном итоге обеспечивает повышение точности обнаружения соответственных точек.

Заключение

Показана возможность достижения более высокой точности формирования фундаментальной матрицы и определения соответственных точек с использованием метода согласованной идентифика ции. К сожалению, вычислительная сложность метода согласованной идентификации выше, чем у алгоритма RANS АС, однако это не является серьёзным препятствием для применения метода, т.к. достижение максимальной точности обычно является важнейшим требованием. Кроме того, при реализации на многопроцессорных системах это не является серьёзной проблемой, т.к. алгоритм обладает высокой степенью параллелизма.

Работа выполнена при поддержке Министерства образования и науки РФ (ГК № 07.514.11.4105), РФФИ (проекты №№11-07-12051, 11-07-13164) и гранта Президента РФ № 4128.2012.9.