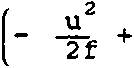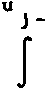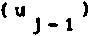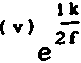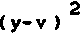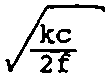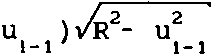Метод согласованных прямоугольников для расчета фокусаторов в плоскую область

Геометрооптическому расчету фокусаторов в фокальную кривую посвящено большое число работ [1,2,3,4]. Расчет фокусаторов в плоскую область геометрооптическим методом менее исследован. Фокусировка освещающего гауссового пучка в прямоугольник рассмотрена в работе [5] геометрооптическим методом, а в работах [6,7] численно исследована градиентными методами. Общего метода расчета фокусаторов в плоскую область в настоящее время не разработано. В данной работе предложен новый численный истод расчета и полного исследования фокусаторов в сложные плоские области.

• 2.    ПОСТАНОВКА ЗАДАЧИ ФОКУСИРОВКИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ В ПЛОСКУЮ ОБЛАСТЬ

• 3.    ГЕОМЕТРООПТИЧЕСКОЕ РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ ФОКУСИРОВКИ В ПЛОСКУЮ ОБЛАСТЬ

Для уяснения физической сущности задачи фокусировки лазерног излучения рассмотрим рис. 1. На фокусатор Ф с апертурой G плоскости и = (и, v) падает пучок лазерного излучения с интенсивностью IQ(u)» эйконалом $о(и), т. е. с комплексной амплитудой

WQ (и) = / 1о (и) ехр [1кФо(и)], где к =-^-. X - длина волны.

Рис. 1. Геометрия задачи фокусировки

В дальнейшем предполагается, что область G соответствует форме сечения падающего пучка. Требуется сформировать в области фокусировки D плоскости х = (х-У) волновое поле с заданным распределением интенсивности 1(х). Решение задачи фокусировки сводится к отысканию фазовой функции фокусатора <Р(и), обеспечивающей формирование требуемого волнового поля из освещающего пучка.

Геометрооптическая фазовая функция фокусатора <рД в "^аксиальном приближении может быть получена из решения следующе системь _р r <р(и) = ад^) - ^0(и)] X = U + f у = V + f * I (5)

< (“)

< у' ' < У и I фокусировки.

1(Х) х' = у' , U       V где f - расстояние до плоскости

Решение вышеприведенной системы (1) в общем случае задача. Геометрооптическое решение задачи фокусировки существенно Упрощается для прямоугольной апертуры фокусатора G. прямоугольной области Фокусировки D при условии факторизуемости функций w0(u) = W](u)W2(v). I(x) = 1,(х) 12(У).

то есть I_o(3) = I_O1(U)I_O2(V). Ф_о(^ = »_0l(u) ⁺ *O2^(V).

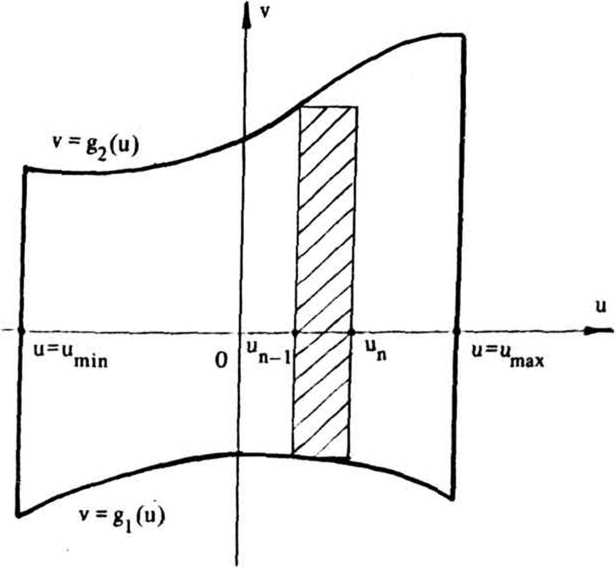
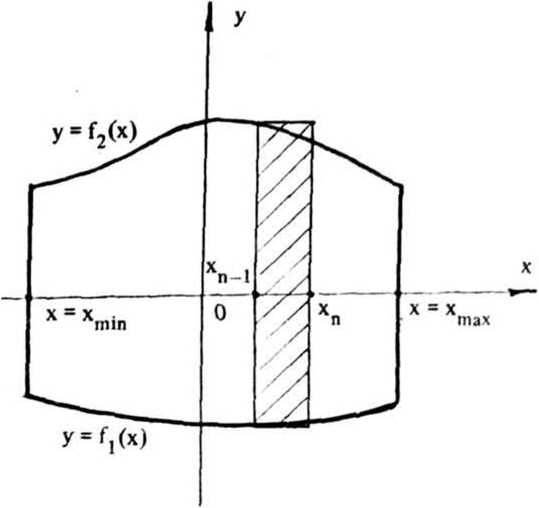
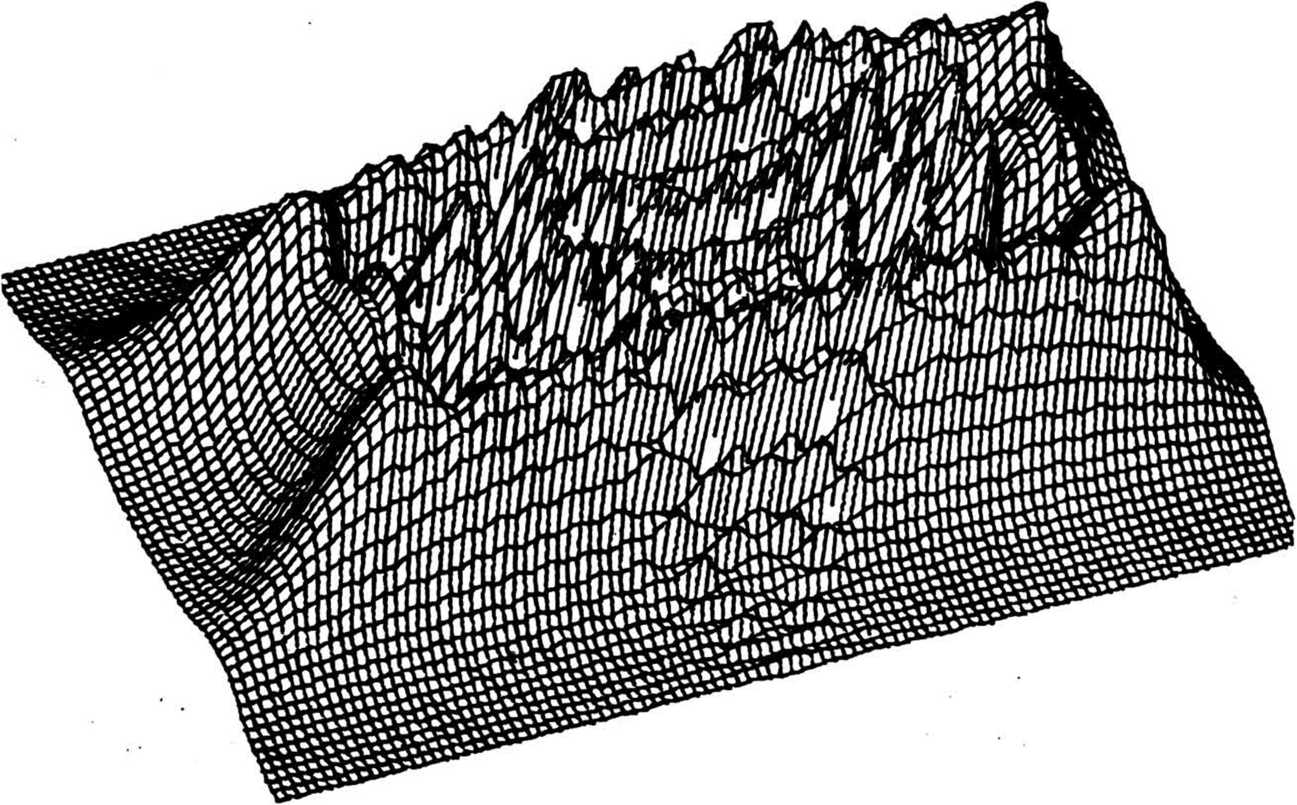
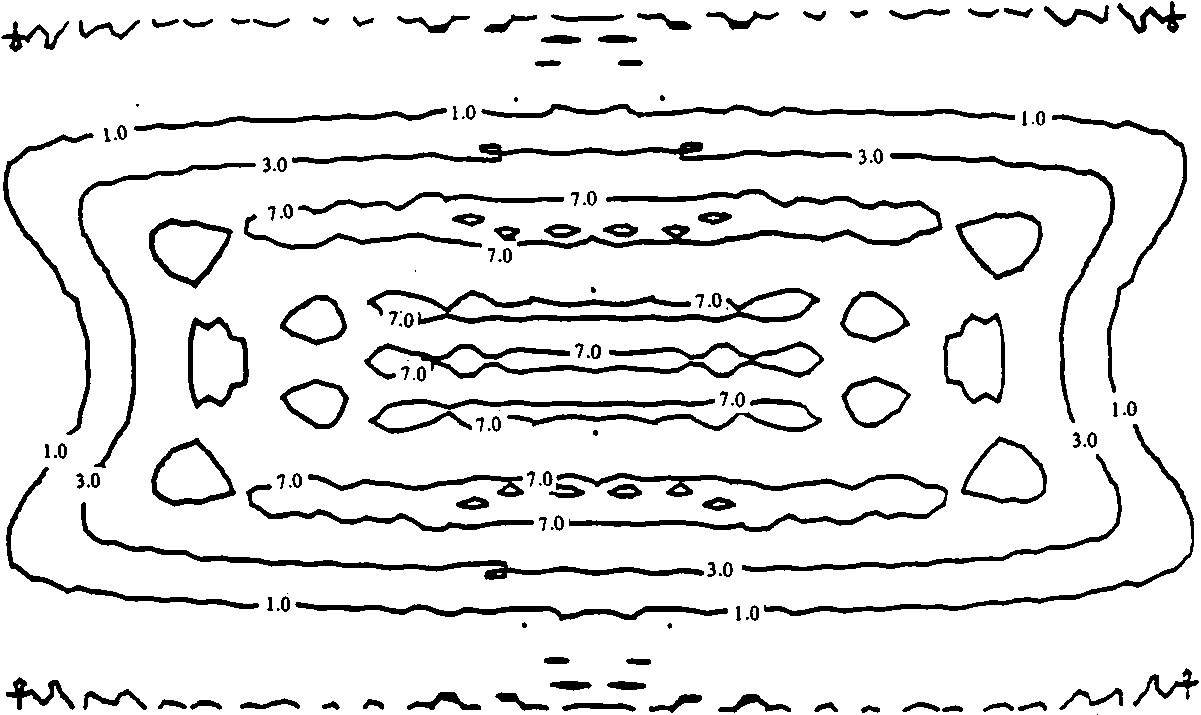
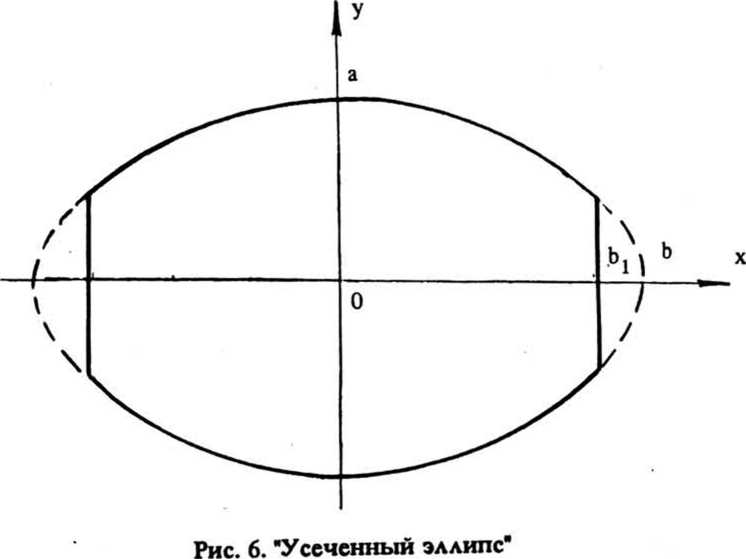
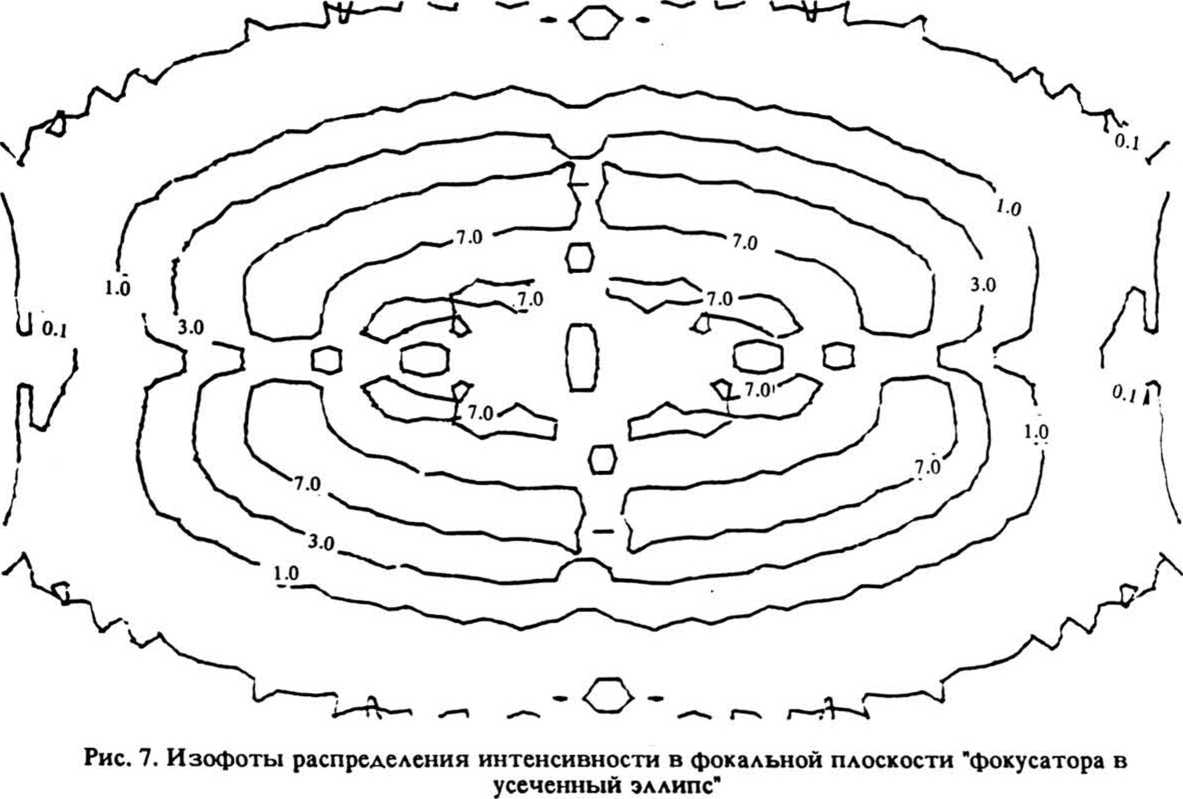
В этом случае решение двух одномерных задач позволяет определить двумерную фазовую функцию фокусатора <р(5) = ^(и) +

Фазовая функция Ф_х(и) одномерного (цилиндрического) фокусатора, осуществляющего заданное преобразование светового пучка, определяется из следующей системы уравнений:

Решение системы уравнений(2) существенно проще, чем решение системы уравнений (1). Например, для случая

I (х) = f I , х s х s х

Iх' 4  10      1

I 0, иначе решение системы уравнений (2), имеет вид:

Ф_х(и) = к

4- П г, fv^ - \Н" ^(и))

и, следовательно, двумерная фазовая функция фокусатора с прямоугольной

апертурой в прямоугольную область фокусировки с постоянным распределением интенсивности имеет вид:

фЙ) = к

1 Г Г 1 Г

⁺ т] [т J ^Io.'¹»^d7> - ^xo]^di^⁺

ти. По этому методу область G и область D аппроксимируются наборами прямоугольников Gj и D , i = 1, N соответственно, и решается задача фокусировки из G в D . Таким образом, апертура фокусатора приближается на-н бором G = U Gf апертурных прямоугольников G^ область фокусировки N

D также приближается набором D = U^ Dt соответствующих фокальных прямоугольников D . Функции 1о(5), 1^5) предполагаются продолженными в области G и D соответственно. Для каждого прямоугольного сегмента Gj рассчитывается фазовая функция ф^ (it), обеспечивающая фокусировку излучения в соответствующий фокальный прямоугольник D^ Рассмотрим описанный способ расчета более детально.

Пусть апертура фокусатора G ограничена кривыми V = g^u), V = g2(u)

и прямыми u = u , u = и (рис. 2), а область фокусировки D - кривыми mln           max у = f (х), у = f (х) и прямыми X = X . X = х (рис.3).

1                 2                               Bin           вех

Рис. 2. Апертура фокусатора

Рис. 3. Область фокусировки

Введем разбиение u., i = О, N, и = и , , и = и отрезка (и , и ] 1                  О min N max              и mln max и апертурные прямоугольники Gf = [u , uf ] x (g^u^), g2(u[ J]. Разбиение x , i = 0, N, x = x , x = x отрезка [x , x 1 1                          0 mln        N max                        mln max'

определяется из решения следующего нелинейного рекуррентного уравнения:

"i ^‘“l-l’      Х1 V^-l1

J JlQ (it) d2^ = J Ji (St) d2x .                      (4)

u □ (u )           x Г (x )

1 -1 9 1 1-1         1-11 1-1

Уравнение (4) получено исходя из сохранения светового потока при распространении света из апертурного прямоугольника G^ в соответствующий фокальный прямоугольник D^

W

g

J2

g

2-к(х-и) 2f du ,

10 „ e J2

dv.

В случае синтеза фокусатора плоского пучка в область с постоянным распределением интенсивности фазовые функции ф^(и), P_J2(^V) содержат квадратичные и линейные по u, v члены соответственно, и, следовательно, вычисление интегралов W^, Проводится к интегралу вида:

+ х и + -1^2Н2_) 1 du. о 2      '

Путем

несложных преобразований можно получить:

где

Кх;^. е2.с,ио,хо)

/2f   2

Тсс" е

Г 2Г о е

[sign(7) С(у) - signCz^CUJ +

sign (x) =

1,

О,

X = о

1, x < 0 ,

/кс . _

У у 2f (^2

2 О

о

i^sign(y)S(y) - signf/JS^)

U

о

X о

с

X

С

и о

х о

с

X с

С(х), S(x) - интегралы Френеля,

о

I sin(t2) dt. о

Используя (9), поле от фокусатора плоского пучка в произвольную плоскую область с постоянным распределением интенсивности можно представить в виде:

kelltf м г                         х - х

w(x) =            Л   * I(x; u , и , —----l^L  и    х

2Л1Г О J = 1  [               j-i> j»  Uj- u '   j-t,  xj-i) x fjx, J - f (x )                 <10)

• ¹    J-i' V j-i'* g u J - g (u )’

• 2    j-i'        ' j-i'

• 7.    РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА

М^-Л fi

Для характеристики качества фокального изображения используются следующие величины: значения энергетической эффективности Р и среднеквадратичного отклонения интенсивности б. Величина

JJl(3)da3

Л1.^*

характеризует долю энергии пучка, попавшую в область фокусировки. Величина

Решив уравнение (4), получаем приближение области D набором прямоугольников

D, = [X,.,. X,] х [fjx,.,). ^(Х^)], i - 1. N.

Для определения фазовой функции у^ (х? ) = Pu(u) + P12(v) прямоугольного сегмента Gf необходимо дважды решить систему уравнений вида (2).

Фазовая функция фокусатора н               / 2u-(ut t+ uK

VW =,?! ^(u, v)rect               | x x rect

( ^2V~ Qi <^u,-,) ♦ у\Л I ^O,.,) - s^.J J

k l»0(u, v).

где rect (u)

0,

терпит разрывы вдоль интерференции на стыках величины интерференционных

прямых u = u^ i = 1, N-1, что приводит к прямоугольников фокусировки. Для уменьшения эффектов фазовую функцию ф(3) можно сделать непрерывной вдоль некоторой кривой v = f(u). Для этого положим

1 -1

где ф= 0, ^ = Е

^,(3) = <Р,(Й)+ q>_f

[y^u^ f (и^ ) - yj41(ujf f (up ) ].

• 5.    СИНТЕЗ ФОКУСАТОРА ПУЧКА КРУГЛОГО СЕЧЕНИЯ

В ПРЯМОУГОЛЬНИК С ПОСТОЯННОЙ ИНТЕНСИВНОСТЬЮ

В качестве примера рассмотрим синтез фокусатора с круглой апертурой, фокусирующего освещающий пучок круглого сечения с плоским волновым фронтом в прямоугольник с постоянной интенсивностью («круглый фокусатор в прямоугольник»).

Интенсивность освещающего пучка имеет вид:

'I 3 € G - 0

(о, u £ G , где G — -|(u, v) |u + v s R j- - апертура фокусатора;

R — радиус освещающего пучка.

Интенсивность в фокальной области I (х) = /1» х € О

(О, иначе,

[ а> а] область расположения фокального прямоугольника.

В данном случае область G приближается набором прямоугольников

°! " (“,.,• U,] X [V^2- ц2 ' , . v^_ u2 ' ,

IN»                1-1        1-1J о ^’ un ^’ a область D - набором прямоугольников

^D! = [x^^ xj x [-a, a], i = 1, N, x_q = -b, x_n = b.

Решение уравнения (4), определяющее разбиение фокальной области, имеет вид:

I (и -

О ' 1

1а

, i = 1,

N-1.

Фазовая функция ^(Заявляющаяся геометрооптическим решением задачи фокусировки прямоугольника G_} в прямоугольник D^ может быть легко получена из (3), причем содержит квадратичные и линейные по u, v члены. Для синтезируемого фокусатора фазовая добавка ф ₁выбирается из условия непрерывности фазовой функции вдоль оси и:

О, i = 1

1 -1

У [ф (U ,0)-ф (и 0)], 2 5 i S N.

• 6.    ДИФРАКЦИОННЫЙ РАСЧЕТ

Работоспособность вышеприведенного подхода к расчету фокусаторов может быть исследована средствами вычислительного эксперимента. В связи с этим ниже будет рассмотрен метод дифракционного расчета поля от синтезиро-рованных фокусаторов плоского пучка в область с постоянным распределением интенсивности. Для расчета поля в фокальной области будем использовать параксиальное приближение интеграла Кирхгофа

1k .->->. 2

W($) = ^ J j-Adbe-^-’e” (X"U) d= 3,

G где W(x) — комплексная амплитуда в плоскости фокусировки;

А (и) — амплитуда падающего пучка;

R0(5) — фаза пучка за фокусатором.

Будем предполагать интенсивность освещающего пучка постоянной, А(3) = A_q, а волновой фронт - плоским, 0_q(3)= 0. Фазовую функцию фокусатора ф(п) считаем определенной согласно равенству (5). Тогда, по равенству (6), поле в фокальной области можно представить в виде:

где ф^и) - фазовая функция сегмента G^.

Учитывая факторизуемость функций е j = 1, N, выражение (7) приводят к виду:

Рис. 4. Распределение интенсивности в фокальной плоскости фокусатора в прямоугольник

Рис. 5. Изофоты распределения интенсивности в фокальной плоскости фокусатора в прямоугольник

Расчет поля от «фокусатора в усеченный эллипс» проводился по формуле (10) при X = 10,6 мкм, f = 800 мм, радиусе освещающего пучка R=20, 5 мм для следующих характерных размеров усеченного эллипса: а = 2 мм, Ь = 4 мм, b * 3,5 мм. Энергетическая эффективность фокусировки в усеченный эллипс составила 87,6%, а среднеквадратичное отклонение интенсивности - 38,2%.

На рис. 7 представлены изофоты трехмерного распределения интенсивности при фокусировке в усеченный эллипс.

Результаты вычислительного эксперимента подтверждают работоспособность разработанного метода «согласованных прямоугольников» при геометрооптическом расчете сложных фокусаторов.