Метод совместного применения дробно-интервальной предварительной коррекции и расширения спектра цифрового сигнала для PLC-сетей и беспроводных каналов связи
Автор: Багманов Валерий Хусаинович, Любопытов Владимир Сергеевич, Султанов Альберт Ханович, Тлявлин Анвар Зуфарович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 3 т.10, 2012 года.
Бесплатный доступ
В статье рассматривается метод обработки цифрового сигнала на передающей стороне канала, предусматривающий совместное применение дробно-интервальной коррекции и расширения спектра сигнала. При этом одновременно решаются две основные проблемы обеспечения надежной передачи цифрового сигнала по искажающему каналу с аддитивным шумом, имеющим сосредоточенный спектр: предварительная коррекция компенсирует межсимвольную интерференцию, возникающую из-за искажений в канале, а расширение спектра позволяет повысить помехоустойчивость приема. Проанализирована эффективность применения данного метода с точки зрения минимизации вероятности ошибки при приеме и мощности передаваемого сигнала.
Межсимвольная интерференция, линейные искажения, предварительная коррекция сигнала, цифровая обработка сигнала, расширение спектра
Короткий адрес: https://sciup.org/140191562
IDR: 140191562
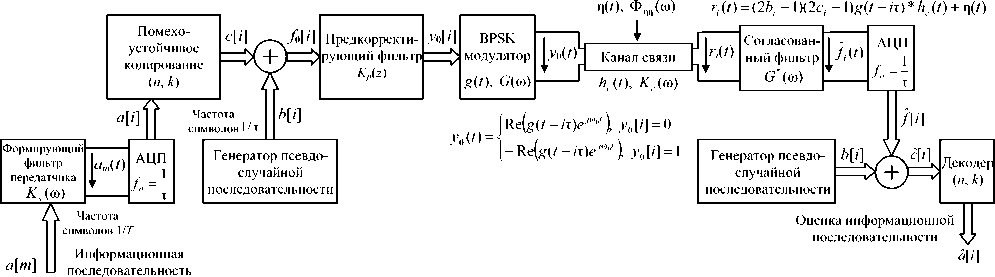
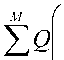
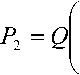
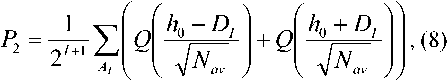
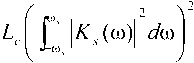
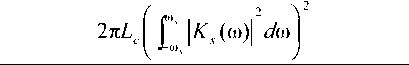
Список литературы Метод совместного применения дробно-интервальной предварительной коррекции и расширения спектра цифрового сигнала для PLC-сетей и беспроводных каналов связи
- Hrasnica H., Haidine A., Lehnert R. Broadband Powerline Communications Networks. John Wiley & Sons, Chichester, 2004. -275 p.
- Dostert K. Powerline Communications. Prentice Hall, New Jersey, 2001. -352 p.
- Fischer R.F.H. Precoding and Signal Shaping for Digital Transmission. John Wiley & Sons, New York, 2002. -492 p.
- Adaptive Equalization/Quereshi S.U.H.//Proceedings of the IEEE. Vol. 73, № 9, September 1985. -Р. 1349-1387.
- Proakis J.G. Digital Communications. McGrawHill, New York, 2001. -928 p.
- Ungerbock G. Fractional tap-spacing equalizer and consequences for clock recovery in data modems///IEEE Transactions on Communications. Vol. 24, August 1976. -Р. 856-864.
- Qureshi S.U.H., Forney G.D. Performance and properties of a T/2 equalizer//National Telecommunications Conference, Los Angeles, CA, December 1977. -Р. 11:1.1-11:1.9.
- Gitlin R.D., Weinstein S.B. Fractionally-Spaced Equalization: An Improved Digital Transversal Equalizer//The Bell System Technical Journal. Vol. 60, № 2, February 1981. -Р. 275-296.
- Hamid K., Stuber G.L. A Fractionally Spaced MLSE Receiver//Proc. IEEE Intern. Conf. Commun. (ICC’95), June 1995. Vol. 1. -P. 18-22.
- Jingxian Wu, Yahong Rosa Zheng, Khaled Ben Letaief, Chengshan Xiao. On the Error Performance of Wireless Systems with Frequency Selective Fading and Receiver Timing Phase Offset//IEEE Transactions on Wireless Communication. Vol. 6, №2, February 2007. -P. 720-729.
- Sultanov A., Tlyavlin A., Lyubopytov V. Method for Linear Distortion Compensation in Metallic Cable Lines//17th International Work-shop EUNICE 2011 «Energy-Aware Communications». Dresden, Germany, September 2011 Proceedings. Springer-Verlag, Berlin Heidelberg, 2011. -P. 195-198.
- Кабанихин С.И. Обратные и некорректные задачи. Новосибирск: Сибирское научное издательство, 2009. -457 с.
- Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. -284 с.
- Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа, 1983. -536 с.
- Анго А. Математика для электро-и радиоинженеров. Пер. с франц. М.: Наука, 1964. -772 с.
- Сергиенко А.Б. Цифровая обработка сигналов. Спб.: «Питер», 2002. -608 с.
- Simon M.K., Omura J.K., Scholtz R.A, Levitt B.K. Spread Spectrum Communications Handbook. McGraw-Hill, Inc., New York, 2002. -1229 p.
- Pickholtz R.L., Schilling D.L., Milstein L.B. Theory of Spread-Spectrum Communications -A Tutorial//IEEE Transactions on Communications. Vol. C0M-30, № 5, May 1982. -P. 855-884.
- Теория электрической связи: Учебник для вузов. Под ред. Д.Д.Кловского. М.: Радио и связь, 1999. -432 с.
