Метод спектральной динамической жесткости в задачах флаттера составных пластин

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2023PNRPU MECHANICS BULLETIN

Во многом благодаря явлению панельного флаттера теория динамической устойчивости пластин в сверхзвуковом потоке газа стала предметом пристального внимания научной общественности, начиная с середины прошлого столетия. Существенный вклад в математическое описание этого явления и его понимание внесли работы А.А. Ильюшина, который впервые представил проблему флаттера как проблему аэроупругости в рамках линейного приближения поршневой теории (закон плоских сечений) [1; 2]. Основные результаты по панельному флаттеру пластин представлены в [3; 4]. Заметим, что даже в рамках линейного приближения задача о динамической устойчивости прямоугольных пластин имеет точное аналитическое решение [5–7], лишь когда две противоположные стороны пластины шарнирно оперты либо в случае цилиндрического изгиба панели. Только тогда переменные в разрешающем дифференциальном уравнении разделяются, и оказывается возможным получить решение в форме ряда. В случае других граничных условий, тем более в случае геометрии, отличной от прямоугольной, для решения задачи используются приближенные аналитические методы и численные методы.

В частности, Olson [8] одним из первых применил конечно-элементный подход (FEM) для решения проблемы флаттера. Yang и Han [9] используют FEM для исследования флаттера термически нагруженных плоских панелей. В работе Prakash и Ganapathi [10] также рассмотрен конечно-элементный подход к исследова- нию панельного флаттера с учетом температурных характеристик газовой среды. Librescu и др. [11] представили исследование флаттера длинной тонкостенной цилиндрической панели в сверхзвуковом потоке. Singha и Mandal [12] исследовали флаттер многослойных композитных пластин и цилиндрических панелей. В работе Bismarck-Nasr и Bones [13] рассмотрены стабилизирующие эффекты структурного демпфирования в задачах флаттера. Song et al. [14] исследуют флаттер плоских консольно-защемленных пластин со структурной нелинейностью в сверхзвуковом потоке газа. Mei et al. [15] используют Fluid-Structure Coupling Algorithm для более точного учета влияния характеристик потока на флаттер панели на основе уравнений Навье – Стокса. В работе [16] представлены результаты эксперимента и численного моделирования для косоугольной панели. Во всех указанных работах авторы используют численный подход при моделировании. Однако, как было замечено в [17], в задачах флаттера применение традиционных численных методов, в том числе метода конечных элементов, зачастую оказывается малоэффективным. По этой причине для задач аэродинамической устойчивости продолжают развиваться аналитикочисленные подходы (обзор работ и описание можно найти в монографиях [1; 2; 4; 5]). Например, в статье [18] метод Бубнова – Галеркина используется для исследования флаттера шарнирно-опертой прямоугольной пластины переменной толщины, этот же метод используется в работе [19] для исследования флаттера стенки топливного бака, в качестве базисных функций берутся комбинации тригонометрических функций. Авторы [20]

используют метод Бубнова – Галеркина для анализа панельного флаттера прямоугольной пластины при наличии сжимающих сил в плоскости пластины. Chen и La [21] также используют метод Галеркина для анализа флаттера и нелинейной динамики композитных пластин. Метод Галеркина был также применяется в [22] для анализа флаттера защемленной ортотропной пластин. Заметим, что сходимость и точность метода Бубнова – Галеркина в задачах флаттера во многом зависят от выбора базисных функций.

Метод динамической жесткости (DSM), который развивается в последние годы для решения задач колебаний и устойчивости, имеет ряд преимуществ по сравнению с FEM, так как опирается на точное аналитическое решение для структурного элемента. Wittrick и Williams разработали [23] DSM для изотропных и анизотропных прямоугольных пластин в случае шарнирно-опертых противоположных сторон пластины на основе точного решения уравнения колебаний. Существенное обобщение DSM для пластин с произвольными граничными условиями было предложено [24], которое дало возможность для анализа сложных конструкций с элементами в форме пластин при произвольных классических граничных условиях. Langley [25] представил формулы динамической жесткости для подкрепленных оболочек. Liu [26] развил идеи [24], предложив формулировки динамической жесткости подкрепленной пластины произвольного сечения при произвольных граничных условиях. В работе [27] представлено обобщение результатов для теории толстых пластин. Поскольку элементы динамической жесткости могут быть непосредственно объединены при моделировании сложных конструкций, а также обладают преимуществами высокой эффективности и точности в широком диапазоне частот, многие исследователи разработали программы и применили их для решения сложных инженерных задач. Williams, Banerjee et al. в сотрудничестве с NASA разработал BUNVIS-RG для анализа вибрации и потери устойчивости сложных стержневых конструкций. Williams, Kennedy и др. разработали VICONOPT для анализа вибрации и потери устойчивости конструкций из композитных пластин. Исследовательская группа Liu разработала программы DSM при поддержке китайского фонда NSFC, которые применялись для анализа вибрации конструкций мостов, многослойных грунтов и строительных конструкций, вагонов высокоскоростных поездов.

Несмотря на значительный прогресс, достигнутый за эти годы, DSM все еще не зарекомендовал себя как достаточно универсальный инструмент, такой как FEM, хотя DSM должным образом признан мощной и точной альтернативой FEM, но, по общему признанию, данный подход на сегодняшний день используется для решения узкого круга задач колебаний. В представленной статье предлагается использовать подход DSM при построении собственных форм колебаний составной пластины для последующего их использования в качестве базис- ных функций метода Галеркина, тем самым расширяя круг приложений на задачи аэродинамической устойчивости.

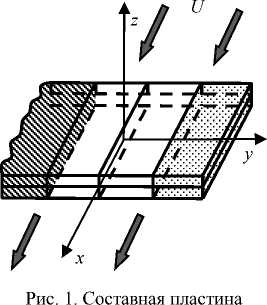
Fig. 1. Combined plate

1. Основные уравнения и структура общего решения задачи

Рассмотрим составную конструкцию (рис. 1), отдельными элементами которой являются прямоугольные пластины из различных материалов и разных размеров толщины h , обтекаемую потоком газа в направлении оси Ox . Для каждой отдельной пластины ансамбля упругие свойства ортотропного материала можно описать при помощи четырех упругих констант: модулей Юнга E ₁ и E 2 вдоль направления осей x и y , модуля сдвига G и коэффициента Пуассона ν ₁₂ . Заметим, что согласно тождеству Бетти, второй коэффициент Пуассона ν 21 можно найти из равенства ν 12 E 2 = ν 21 E 1 .

Уравнение, описывающее аэродинамическую устойчивость, может быть записано следующим образом

„ d⁴ W 4 WW „ d⁴ W , d² W , d W

D —+ 2 2 D 3 —5—7 + D 2 —r + P h—у + sp h --+ P = 0, (1)

1 dx4      3 dx2dy2    2 У44       dr2        dr где W(x, y, t) – прогиб; ρ – плотность материала, ε – коэффициент затухания,

E h 3      ; D =      V 21 E i h ³     ;

12(1-V 12 V 21 );    ²   12v i2 (1 - V 12 V 21 )’

D 3 =

v ₂₁ E 1 h ³       Gh ³

12(1 - V 12 V 21 )⁺ 6

Заметим, что в уравнении (1) упругие коэффициенты D ₁, D ₂ и D ₃ и плотность ρ, вообще говоря, различны для каждой отдельной пластины ансамбля, то есть представляют для составной пластины разрывные функции.

В линейном приближении поршневой теории [1; 2] составляющая аэродинамического давления P может быть выражена через прогиб пластины p = kpo raW+и dW , c0 ( dt      6x )

где p о - давление в невозмущенном потоке, c ₀ - скорость звука в невозмущенном потоке, к - показатель политропы газа, U - скорость потока.

Следуя стандартной процедуре, запишем уравнение (1), отделяя временную составляющую W = w ( x , y )e °* относительно амплитуды прогиба w ( x , y ) в виде

где

U = KP 0L и

U 0        U, c0 D,

X = -^PQ ² - g Q , P

d ⁴ w , „ d ⁴ w „ d ⁴ w K pU d w

Dx —T+2 D3 2 2 + D: 4 + —+ ex4      dx dy     dyc

(         (                 0

+ ст ² p h +ст| ep h +^K p ⁰ I w = 0.

I I

Предположим также, что на сторонах составной пластины реализуется комбинация классических граничных условий: защемление (C) - шарнирное опирание (S) - свободный край (F). Например, на сторонах вида x = а эти условия для тонкой ортотропной пластины могут быть записаны в форме

(С) полное защемление w = о;    ■ = 0, dx

I h        K p ₀

g = ^ep J — ⁺    p=— .

V ^D 1 P c 0 V D 1 P h

Заметим, что задача на собственные значения (6) для отдельной пластины достаточно хорошо изучена. Известно [1; 5], что Re X > 0, с увеличением параметра скорости U ₀ собственные значения X последовательно переходят в комплексную область. С учетом введенных обозначений критерием устойчивости движения будет условие

Q² + ^{p g} Q + —= 0;

P P                      (7)

Re Q< 0.

(S) условие шарнирно опертого края w = 0;    w = 0, дxx

(F) условие свободного края ,, С d ² w d ² w ) „

M, = - D -- T + V]2- D 2 -- T = 0;

x ( ¹ d x ^{2    12 2} d y ² )

Предположим далее, что известна система собственных функций пластины { w “ ( x , y ) } в вакууме, соответствующая собственным частотам колебаний {ю m } при тех же граничных условиях, что и исходная задача аэроупругости. Тогда будет верно, что

84 и0      54 w0     54 w0

D1 -wm+2 D3 —-^+D2 -wm=D1®mwm.(8)

8x      dx dy

<

In ⁵ ' w L Gh ³ 1 d ³ w I л

Vx =- D\—? + 1 D₃ + I--- 2 = 0.

Id x ³ (       6 ) d x d y )

Следуя процедуре метода Бубнова - Галеркина [1], решение задачи будем искать в виде ряда по системе собственных функций составной пластины в вакууме

На сторонах пластины вида y = b граничные условия записываются аналогично.

Исследование задачи на собственные значения для (3) при указанных граничных условиях позволяет ответить на вопрос об устойчивости колебаний. Действительно [1], колебания пластины будут устойчивы при Re ст < 0 и обратно, при Re ст > 0 являются неустойчивыми.

Обозначим как р l и D 1, l - плотность и цилиндрическую жесткость в направлении оси Ox каждой отдельной пластины ансамбля, тогда плотность и цилиндрическая жесткость в данном направлении составной пластины могут быть записаны как

№ w (x, y) = Z A™w0( x, y).               (9)

m = 1

Форма решения (9) такова, что удовлетворяет краевым условиям на сторонах составной пластины, таким образом, остается выполнить разрешающее дифференциальное уравнение (6). Подставим (9) в дифференциальное уравнение (6), тогда, учитывая дифференциальное соотношение (8), получаем равенство

№                        № °ллР

2 A n ( х-ю . ) w 0 = U 0 2 A n ^w^ n = 1                            n = 1 ^d x

р = 2 S р , ; D 1 = E S-D„          (4)

l S l S

где S l и S - площади l -й составляющей и всей составной пластины соответственно.

Тогда частотный параметр может быть записан в форме

Учтем также, что собственные функции { w m ⁽ x , y ) } являются ортогональными в функциональном пространстве интегрируемых с квадратом функций в области K , которую занимает составная пластина, то есть при m * n :

Q =P h ст 2 . D

jj w m w ⁰ dxdy = 0.

K

А уравнение (3) может быть представлено в виде

„ d4w п d4w ww - dw -„

ЦтТ + 2 D3 2д.2 + D21TT + U0 Д™ = DX w dx      dx dy     dy

Умножая (10) на wm(x, y) и интегрируя по области пластины K с учетом ортогональности (11), получаем однородную бесконечную систему линейных алгебраических уравнений вида to

Y m ( X-» m ) A m = U 0 Z M mn A n , ( m = 1, 2, ---), (12) n = 1

d w ⁰

где ^Mmn = JJ w m     dxdy ; Y m = JJ ( w m )² dxdy .

K    ^{d x}            K

Очевидно, что при практической реализации уравнения (12) дают задачу на собственные числа λ для матрицы с элементами

^Л N   I ^ mn ® m

N

+ U 0 M mn |

Y

' ^m       m , n = 1

(^mn — символ Кронекера) при N ^ ю, а определитель матрицы det (Лn -XEn ) = 0

может рассматриваться как дисперсионное уравнение для определения собственных чисел λ.

В [1] доказывается сходимость определителя (14) в случае шарнирно-опертых краев прямоугольной пластины (напомним, в этом случае задача аэроупругости имеет точное решение в виде тригонометрического ряда), соответственно сходится и процесс вычисления собственных чисел λ. Для полностью защемленной ортотропной пластины процесс сходимости (14) был исследован в [22] численно, было показано, что удержание N = 16 базисных функций в представлении (9) обеспечивает хорошую сходимость метода Бубнова – Галеркина.

Таким образом, алгоритм исследования устойчивости для составной пластины имеет вид:

• 1)    при заданном значении параметра скорости U ₀ , из (13), (14) определяются собственные значения { X j };

• 2)    для каждого собственного значения X j определяются соответствующие корни { Q j l } квадратного уравнения (7) для каждой l -й пластины ансамбля;

• 3)    проводится проверка корней { Q j l } на устойчивость: Re Q< 0.

• 4)    проходя диапазон изменения U ₀ от нуля с некоторым малым шагом, находится критическое значение параметра скорости U ₀ ^кр , при котором одно из значений { Q ± l } дает неустойчивость, т.е. Re Q ± l >  0.

• 2.    Метод спектральной динамической жесткости

Рассмотрим структурный элемент в виде ортотропной прямоугольной пластины (рис. 2), колебания которого описываются уравнением (8).

Пусть на границах пластины x = ± a и y = ± b заданы кинематические характеристики ( w , ф _x , ф _y ) и силовые характеристики ( M_x , M_y , V_x , V_y ) пластины в виде

d = ■ Фa W ф; Wa = ■ W( a, у) " фу(a, у) w(x,b) фx ( x , Ь ) W(-a, у) и f = Г V:1 Ma Vb+ Mb V = ■ Vx (a, у ) " Mx (a, у) Vy (x, b) Му (x, b) Vx(-a, у) (15) , ■ Фa фу(-a, у) Ma Mx(-a, у) W_ w( x, -b) Vb Vy (x, - b) _ф-_ _фx (x, -b) _ _ m;_ _ Му (x, - b) _ где, согласно теории тонких ортотропных пластин,

5 w     5 w ф x = ^; фу = ^; о у       о x f d3w

V =— D . + (Di + 2 D6 б) x 1366 ( dx d3 w dxdу у

f   d3w

V y = —^2     + ( D 3 + 2 D 66 )

I   d У 3

d ³ w d x ² d у

( d2w

Mx =— D ^ + D 2

x I ¹ d x ^{2      12}

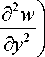
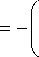
d ² w

² Я 2 ⁺ D 12 d у

d ² w ix^

M y

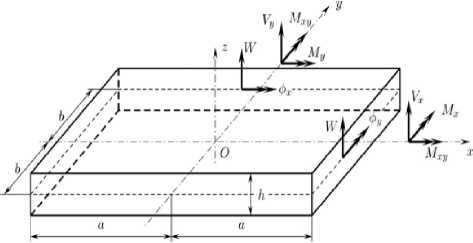
Рис. 2. Структурный элемент в виде прямоугольной пластины

Fig. 2. Structural element in the form of rectangular plate

Далее введем разложение этих величин в ряды по модифицированной тригонометрической системе функций { T k }:

1 to d = ZZ k=0 n=1 WankTk (в пку) ф+X (впку) Wb+kTk (ankx) ф+X (a nkx) 1 to и f = ZZ k=0 n=1 ■v+kT (в„kУ)" MankTk (в „kУ) Vb+kTk (a nkx) MbnkTk (a nkx) , (19) Wan Tk (вnkX) Va-kTk (вnkУ) ф -nTk (в „ку) м;Х (в „у) Wb-kTk (a nkx) Vb-Tk (a nkx) _ф-kTk (ankx) _ _ M_X (a nkx) _ где тригонометрические функции Tk в зависимости от типа симметрии определяются следующим образом

T k ( z ) = cos

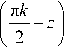
cos z , sin z ,

k = 0 1 k = 1

Константы разделения в (19) выбираются в форме п ( ,   к)   „     п (, а nk = -|n -1 + ^1,  e nk = т|и -1 + ^1 • a I       2)         b <

Заметим, что при подобном выборе, вне зависимости от типа симметрии, будет верно

T k ( a ^a ) = T j ( в j ) = ( - 1) n ^{+ 1} и T>^a ) = Г / ф n b ) = 0.

Под спектральной динамической матрицей жесткости пластины будем понимать такую, вообще говоря, бесконечную матрицу K , которая дает связь между коэффициентами Фурье кинематических и силовых граничных характеристик (19).

f = К " d s ,                     (22)

где

1      ( +0     + 1 + 0 + 1     + 0     + 1 + 0 + 1     - 0

d s = { w an , w an , ф an , ф an , w bn , w bn , ф bn , ф bn , w an ,

-1 ^-0 -1 . -0 . -1 _-0 -1) от wan , фan , фan , wbn , wbn , фbn , фbn } , , n = 1

f =S,V ⁺⁰ F⁺ⁱ M⁺⁰ M⁺ⁱ F⁺⁰ F⁺ⁱ M+° M+' F^-0 F^-'

J s [ an , an , an , an , bn , bn , bn , bn , an , an , м-0 m-' f-0 F-1 м;0 м-1 Г an , an , bn , bn , bn , bn n ==' .

В частности, общее решение для уравнения колебаний (8) может быть построено с учетом обозначений (20) для всех четырех случаев симметрии в виде от w = Z (AnHj (Pnky) + BnHj (pnky))Tk (ankx) + n='                                                    (23)

от

+ Z ( CH ( q nj X ) + D n H k ( j )) T j (в п, у ), n = 1

где H ₀ = ch( z ) и H 1 = sh( z ).

Величины p_nk , p k и q_nj, q j являются корнями следующих характеристических уравнений

D ₂ p ⁴ - 2 D ₃a ² p ² + D 1 a ⁴ - Ди² = 0, D 1 q ⁴ - 2 D ₃ p ² q ² + D ₂P ⁴ - Дю² = 0.

Из предыдущей статьи [24] можно увидеть, что анализ каждого случая симметрии представляет собой отдельную задачу, при этом приходится отдельно удерживать слагаемые, отвечающие постоянным составляющим в тригонометрических разложениях. Предложенная форма общего решения (23) позволяет унифицировать эти выкладки и получить единообразные выражения для всех случаев симметрии.

Далее, вычисляя углы поворота и сдвиговые силы по (16), (17), получаем от фy = Z(AkHj (Рп1У) + BkHj (pnky))ankTk(ankx) + n='                                                     (24)

от

+ Z ( C nk q n H k ( q nj X ) + D j ( q nj X ))T j (P n y );

n = 1

фx = Z(AkPnkH‘ (Pnky) + BkPnkH‘ (Рп1У))Tk (ankx) + n='от

+ Z ( C nk H k ( q nj X )+ D nk H k ( q nj X ))P nj T /(P n y ); n = 1

V x = Z A k T D ' “ nk - ( ^D3 + ^{2 D}66 )P nkk ] H ( P nk y ) +

+ Bk [D,«2k -(D3 + 2D66)P2 ]H,(pnky))a„kT/(a^x) +

+ ] * ! ( C k q n, [ ( D 3 + 2 D 66 ) P 2 , - D,q ² ] H k ( q nj x ) +

+ D nk q nj [ ( D 3 + 2 D 66 ) P nj - D ' q 2 ] H k ( q j x )) T (P nj y );

V y =^Z( A k P k [ ( D 3 + 2 D 66 ) a 2 k - D 2 P nk ] H j : ( P nk y ) +

+ BkPnk [(D3 + 2 D66)a2k - D, p2 ] Hj( pnky ))Tk (a^x) +

+] = : ( C k [ D 2 P 2 j - ( D 3 + 2 D 66 ) q ² ] H k ( q nj x ) +

+ D k l D 2 P 2 j - ( D , + 2 D 66 ) q j ] H k ( qj x ))P, T '(P, y ).

Выразим неопределенные коэффициенты C и D k для каждого случая симметрии ( k , j ) через коэффициенты разложения величин ф _y ( ± a , y ), V_x ( ± a , y ). Приравнивая записанные выше выражения с граничными разложениями (19), складывая и вычитая данные равенства, получаем систему четырех уравнений относительно неопределенных констант C nk и D nk :

C°^Jq k_J H ' ( q nj a ) + D ° ^j q k, H ' ( qja ) J^n-^L ;

C'qnjHi'( qnja)+D'qnjHX q„ja) = ф+n +ф -nj.

2 ;

Cn¹ q nj [ ( D 3 + 2 D ₆₆) P nj - D i q n , ] H 0 ( q nj a ) +

V + j - V

+ D j q j [ ( D 3 + 2 D ₆₆) P nj - D i q^H 0 ( q₄a ) = ^{V a}^ -V ^a

C 1 q j [ ( D 3 + 2 D ₆₆) P n. - D i q 2 j ] H ' ( q nj a ) +

V + j + V - + D nj q nj [ ( D 3 + 2 D ₆₆) P 2 j - D i q ² ] H ' ( q nj a ) = ^a 2 ^a

Из данных соотношений можно выразить константы C_n^kj и D_n^kj следующим образом

C k q nj H k ⁽ q nj ^a )

D k q nj H k ⁽ qj a )

D i q ^2-( D 3 + ^{2 D} ₆₆) p nj. _ . +       1       , V k ;

^D i ⁽ q n ^{2 -} q j       ^{an D} i⁽ q j ^- q nj' ) ^an’ (28)

_ D i q 2 ^{- (} D 3 ^{+ 2 D} ₆₆) P nj _mkj         i        _Kkj

D1(q2 -q2)      'фan   D1(q^ -q2) an, k .ф +l - (-')kф-j  yk  v:nj - с-pkVn де фan                       , Van

Аналогичным образом можно выразить величины A k , B nk через коэффициенты разложений (19) величин ф x ( x , ± b ) и V y, ( x , ± b ) как

. kJ p и'(п кх- D² p   ( D³ + ² D66 ) ^ank , .j

A j p nk H j ⁽ pnkb ) =       „ ,-2     2 \      ^ф bn +

^D 2⁽ Pnk ^- Pnk )

¹ jt¹-'^bn ’

D 2 ⁽ pnk ^- pnk )

D kj-kk —  D2 ^Pnk  ⁽ D^{3 + 2 D} 66^{) a} nk j

B n p nk H j ⁽ pnkb ) = П^ф bn - D 2⁽ P jk - P jk )

H k ⁽ q j a ) [ D, 2

Т . н j ( q j a ) ^{L( 1 4nj}

- ( D 3 + 2 D 66 ) P nj ) Ф .j + V an ]l _T -T n y ) . 1 =

-J D X , nj ^- ,nj )

1 »

Ц WjT j ( P n y ).

j = 0 n = 1

D 2⁽ Pnk - p ^k )

kj

' bn ’

Переходя далее к двум равенствам для выражений w (a, y) ± w (-a, y)

2            ’

можно получить следующие соотношения

⁺ k -f-IV, ^k        JZ+ k -f-lV V- k

PUP m kj — ф bn ( 1) ф bn k/kj _ V bn    ( 1) V bn где фbn =       ~       , Vbn =        ~

Используя формулы (28) и (29), функция прогиба пластины w может быть выражена через коэффициенты Фурье граничных характеристик (19) в виде

n = 1

' H j (p . y ) [ ( D 2 p n. - ( D 3 + 2 С б₆ ) « 2 . ) ф .п + v bn - D 2⁽ p n. ^- P* ) P nk^H' j (P nk b )

H j (p . y ) [ ( D 2 p J. - ( D 3 + 2 D 6₆ ) « 2 k ) ф . + V b^nl —

-

w =у щ HPУ¹» [ ( D , p nk - ( D , + 2 D .. ) « 2 k у » + » у- ■     n = 1 [ P nk ^H / ( P nk ^b ) ^{L                                     -}

^H j ⁽ p , y )

-^^--x

P nk H j ( P nk b )

x[ ( D.. p j. - ( D , + ² D kti ) ф i+ V ]} DTj ,) +

+ j - H T T n ^[ ( DA. - ( D , + 2 D .) ₽; ) ф j + V l ]-[ , nj ^H j ⁽ A nj a ) ^L

⁽ p jk ^- p j. ) P nk H j ( P nk b )

> ( - 1) ^{n + k} +

*

2 ] n = 1

' H k ( , nj a ) [ ( Dq jj - ( D 3 + 2 D 6₆ ) P 2 j ) v kn + V- T nj H j X , nj a )

H . ( T j a ) [ ( Dj - ( D 3 + 2 D 66 ) P 2 j ) v .n + V-	Т ( Р п, у )
q nj H j X q nj a )	D ( q 2 - q jj )

*

= 2 w aj T j ( в nj- y ), n = 1

—^h. ( q nj x ) [/ D 2 - ( D ₊ 2 D ) p₂ \ k, , , H ' ( q^ a ) L^{( 1 ,j 3       66} n ) an

+ V k an

^p n y ) 1 . (30)

D 1 ( q jj ^- q j

где w aj =

w ^{+ j} + (-l) ^k w ^j an an

Подставляя в формулы моментов M_x и M y вместо неопределенных коэффициентов C . , D . ^j и A . , B , представления (28) и (29) через коэффициенты Фурье граничных разложений, получаем, что и значения функции прогиба w , и значения моментов M_x , M_y оказываются выраженными через коэффициенты Фурье граничных значений ф _x , ф y и V_x , V_y . Далее, приравнивая полученные выражения для прогиба w , и моментов M x , M y к их граничным представлениям (19), можно получить связь между коэффициентами Фурье Ф™ , Ф и , ' k, , V bnk ^и коэффициентами w , , w ±. , M , , M b,* .

Рассмотрим вывод подобного соотношения для w ( ± a , y ). Положим x = ± a в формуле (30) и приравняем к соответствующему граничному разложению из (19) w ( ± a , y ) = ]Г J jr ( ^Hj(P ;k ^y) [ ( D 2 p k - ( D 3 + 2 D 66 ) a 2 k ) ф j + kj ) [ n = 1 [ PnkH j⁽ Pnkb ) ^L

+ Vk ]- ^{H ( P}-^ky ) x ^{bn J} P nk H j ( p^b )

x[ ( D 2 P nk - ( D 3 + 2 D 66 ) a 2 k ) Ф kn + V^ (±¹¹-₂^{( - 1)} n ⁺\ +

^{L                                  J}' D 2 ⁽ P nk - P nk )

+ ( ± 1) ^k | ^H^q ^ a- [ ( DT n. - ( D 3 + 2 D 66 ) P 2 j ) v an + v an ]-

[ T nj H j⁽ .T nj a ) ^L                                           ■

Для алгебраизации последнего функционального равенства используем разложение входящих в него гиперболических функций по тригонометрической системе { t . ( в _njy ) } согласно известным формулам [28], которые с учетом введенных обозначений принимают вид

^Hj ⁽ Py ) = p у h J ( pb ) = b T :1

( - 1) т ^{+ 1} ( 2 -5 j o 5 _{l m} ) в т + P ²

T j ( в _m j^p ).

Тогда, подставляя (32) в равенства (31) и меняя порядок суммирования, получаем после алгебраических преобразований первую часть уравнений бесконечной системы линейных уравнений, связывающей коэффициенты граничных разложений

2 -S j o 8 1 . у _{( - 1)} n + m ( D 2 p mj + D 12 a j. ) ф bn ⁺ V ^j ^b D 1    J "1            ^{( a} J. ⁺ q mj )( ^a Jk ⁺ q j )

₊ f H . ( , mj a ) . D 1 q² mj - ( D 3 + 2 D 66 )e mj -

( ^Hk ⁽ , mj a )       , mj ⁽ q j ^- q mj)

- H . ( , mj a ) . D 1 q m .- ( D 3 + 2 D бб )в т ) ф km + ^Hk ⁽ q mj a )       q_m j⁽ q ²,^- q j     ) D 1

+ f , mj^Hk ⁽ , mj a ) I ^Hk ⁽ , mj a )

, mj^Hk ⁽ , mj a ) )      V am

^Hk ⁽ q mj a ) J D 1 ⁽ q m -^- q mj )

= w am .(33)

( m = 1, 2, ^)

Рассматривая граничные соотношения w(x, ± b), Mx (± a, y) и My (x, ± b), можно аналогично получить другие уравнения системы. Если обозначить wbknj

■ + ( i) w b _Mk _; m^ + ( - 1) ^k M - n

, M an

D 2 A m = D 2 p m ^{к (} DD ^{3 +} 2^j⁾⁶ 6 ^{)a mk} Cth j ( P mk b ) - pmk ^{( P}mk - ^Pmk )

_ D 2 pmk - ⁽ D 3 ^{+ 2} D 66 ^)a mk     /— LX.

₂₂     Cth _j ( p _mkb );

pmk ⁽ pmk - pmk )

M kn =

M + + ( 1) M

D 2 ^A m = 2-2 ¹ 2 . ( Pmk ^Cth j ⁽ Pmk^b ) - Pmk ^Cth j ⁽ P mk^b ) ) ; ( P mk - P mk )

данные соотношения можно записать в форме бесконечной системы линейных уравнений

2 -5j05,m       ,+m (D2Pmj + D12< )vj + V bD   £? ^    ^ + qmj )(a2k + q^)

1kj 2kj kj m • am 1 mm’am    wam;

2-5Я5,„ -    n+m ((D — 4D66 — did2 j - D2Dm )vj -(DX + D,ajk) Vk bDi tT )             « + XX + qj

+ Am V km +Amvm =- Mkm;(36)

2 -5к051 m y1 (- 1)n + m (D,amk + D12вnj )vaj + Vai + aD 2  £      (j Pmк Xj Pmк)

+ Am V j +AmVm = wm;(37)

7 = s . DD ,2 - 4 D.2 - D.D, №a2. - D.,D. ш2)®k - ID. ,a2 + D, R2 Vj 2-5 к 05l m у (-1) n+m W 3______66    1 2/ jV mk 12 1 Man У 12 mk 2 ^1 an aD 2    П=1                                  (P2j + Pm к )(P2j + P2k )

7 kj 8 kj kj

^{+ A} m ^V bm ^+A m V bm    ^M bm ;

(m = 1,2,...), где Cthk (z)

H k ( z ) _; н к ( ^ );

2 m

( D 2 P mk к - ( D 3 + 2 D 66 )a mk )( D 2 P m к - D^^ mk ) _m z „ ,x

₂₂             Cth _j ( p_mkb )

P mk ⁽ P m к ^- P m к )

⁽ D 2 P m к ^{- (} D 3 ⁺ 2 D 66^)a mk ⁾⁽ D 2 P mk ^- Dn^ mk )_т z- LX

₂₂             Cth _j ( p _mkb )

P mk ⁽ P mk - P mk )

D 2 A m = D ^{2 P}7_ 2 - D ^'a m* oh j ( P mk b ) - P mk ( P mk - P mk )

- D 2 P m к - D^a kk p mk ( p m к - p m к )

Cth _j ( p _mkb ).

Таким образом, уравнения (35)–(38) определяют связь между граничными значениями кинематических и силовых характеристик пластины, а бесконечная матрица системы позволяет найти спектральную динамическую матрицу жесткости (22), которая в точной постановке задачи также является бесконечной. При практической реализации данная бесконечная матрица приближенно редуцируется в конечную матрицу порядка N .

Процедура стыковки матриц динамической жесткости каждой из пластин ансамбля близка к аналогичной процедуре метода конечных элементов, но с тем отличием, что стыковка проводится не через точечные узлы, а через линии стыковки, в которых полагаем совпадающими кинематические и силовые характеристики.

• 3.    Численные результаты

  1 m

  
  

  1 ^q mj   366 mj

  
  

  ^qmj ^{( q}mj ^{- q}mj )

  
  

  Cth _k ( q_mja )

  
  
  
  

  1 ^qmj   366 mj

  q mj ⁽ q mj ^{- q}mj )

  
  

  Cth _k ( q_mja );

  
  

  D ^A m = _r2¹ 2 x ( q m ,^Cth к ⁽ q mj^a ) ^- q m ,^Cth к ⁽ q mj^a ) ) ; ⁽ q mj    q mj )

  
  

  1 m

  
  

  ( D . q mjj - ( D 3 + 2 D ₆₆)e mj )( D ₁ q mj - DX ) q mj ⁽ q mj - q mj )

  
  

  Cth _k ( q_mja )

  
  

  _-

  
  

  ( D 1 q mj - ( D 3 +2 D 66 )e mj )( D 1 q m, q mj ⁽ q mj - q mjj )

  
  

  D 12 β mj )

  Cth _k ( q_mja );

  
  

  1 m

  
  

  1 ^qmj      12 mj

  q mj ⁽ q mj    q mj )

  
  

  ^Cth к ⁽ q mj^a ) ^-

  
  

  1 ^q mj      12 mj

  q mj -⁽ q mj - q mj )

  
  

  Cth _k ( q_mja );

  
  

  Представленный в статье алгоритм исследования динамической устойчивости составных пластин был реализован в среде пакета Mathematica. При этом на первом этапе для заданных физико-механических и геометрических параметров составной пластины рассчитывались на основе метода спектральной динамической жесткости первые собственные частоты колебаний пластины ω m в вакууме и соответствующие им собственные формы { w m ( x , y ) } , далее реализовывался алгоритм Бубнова – Галеркина, описанный в первом разделе статьи.

  В качестве численного примера рассмотрим составную пластину (рис. 3), левая половина которой – стальная пластина с упругими параметрами р = 7,8 ■ 10³ кг/м³, E = 1,9982 ■ 10¹¹ Па, v = 0,3, а правая половина - алюминиевая пластина с параметрами р = 2,75 ■Ю³ кг/м³, E = 0,7 ■ 10¹¹ Па, v = 0,34. Воздушный поток имеет следующие характеристики p ₀ = 1,0126 ■Ю ⁵ Па, р ₀ = 1,2928

  
  

кг/м 3 , κ= 1,4. . В табл. 1 представлены первые собственные частоты { ω n } данной составной пластины при полностью защемленных краях, вычисленные при помощи метода динамической жесткости.

y

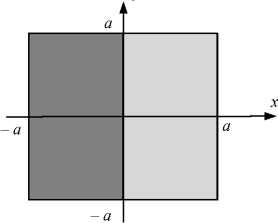
Рис. 3. Составная пластина

Fig.3. Combined plate

Таблица 1

Первые собственные частоты составной пластины (сталь – алюминий) при полностью защемленных краях

Table 1

First natural frequencies of combined square plate (steel – aluminum) with fully clamped edges

N	1	2	3	4	5	6	7	8
ω n Составная пластина (сталь – алюминий)					о.	о"	ОО	О

Собственные частоты пластины в вакууме {ωn} дают возможность, согласно (30), получить аналитическое представление для соответствующих собственных форм колебаний wm0 (x, y) и аналитически вычислить значение интегралов из (12), что позволяет эффективно реализовать алгоритм метода Бубнова – Галеркина. В табл. 2 представлена сходимость этого метода при увеличении числа N, удерживаемых в расчетах собственных форм wm0 (x, y). Толщина пластины в расчетах принималась h/b = 0,0065.

Таблица 2

Сходимость метода Бубнова – Галеркина для составной пластины

Convergence of Bubnoff – Galerkin method for the combined plate

Table 2

N	U 0
8	128,76
12	94,77
16	96,92
20	96,92

Из данных табл. 2 можно увидеть, что N = 8 собственных форм недостаточно для получения достоверных данных, в то время как при N = 16 метод сходится с достаточной точностью. Заметим, что похожая ситуация со сходимостью метода Бубнова – Галеркина наблюдается и для других значений геометрических и упругих параметров задачи. На рис. 4 представлены формы потери устойчивости составной пластины (см. рис. 3) в двух случаях, когда воздушный поток направлен в направлении оси Ox ( a ) и когда воздушный поток направлен в направлении оси Oy ( b ). Можно увидеть, что в обоих случаях вспучивается часть пластины, противоположная направлению потока.

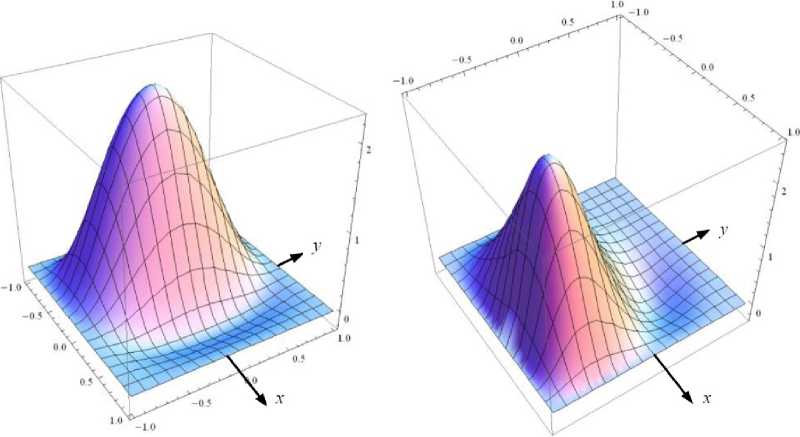
b

a

Рис. 4. Формы потери устойчивости квадратной составной пластины сталь–алюминий: a – U ₀ = 96.22; b – U ₀ = 93,02

Fig. 4. Buckling forms for the square combined plate steel–aluminum: a – U 0 = 96.22; b – U 0 = 93,02

Аналогичную ситуацию можно наблюдать и для форм потери устойчивости у однородных пластин при различных граничных условиях [2; 17; 22]. Составной характер представленной в примере пластины проявляется, скорее, количественно. Так, благодаря тому, что правая половина пластины сделана из более податливого материала (алюминий), в сравнении с аналогичной формой однородной пластины (рис. 5) правая часть составной пластины оказывается более вспученной.

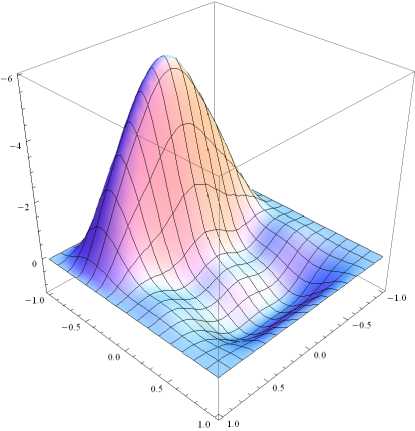
Рис. 5. Форма потери устойчивости квадратной однородной пластины (сталь), U ₀ = 106,39

Fig. 5. Buckling form for the steel square plate, U 0 = 106,39

мость метода Бубнова – Галеркина также наблюдается при удержании в расчетах N =16. На рис. 7 представлены формы потери устойчивости данной пластины при защемленных краях в двух случаях: первый – когда воздушный поток с параметрами р ₀ = 1,0 1 26 - 10 5 Па, р ₀ = 1,2928 кг/м³, к = 1,4 направлен вдоль большей стороны пластины, т.е. по оси Ox , и второй – когда воздушный поток перпендикулярен большей стороне, т.е. направлен по оси Oy .

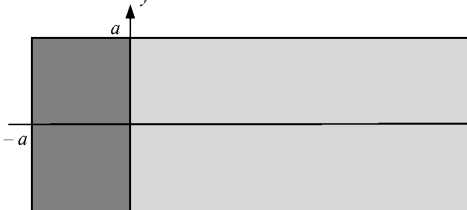
x

4 a

Рис. 6. Удлиненная составная пластина

Fig. 6. Long combined plate

В первом случае получаем значение параметра критической скорости U ₀ = 23,44, во втором случае U ₀ = 67,08. На рис. 7 представлены соответствующие формы потери устойчивости.

В табл. 3 представлена зависимость критической скорости потери устойчивости от безразмерной толщины h/b . В данной таблице для удобства представлен

U UD безразмерный параметр — =----, что позволяет уви-c0    КР 0

деть диапазон применимости результатов в рамках линейного приближения поршневой теории. Можно заметить, что значение критической скорости растет с увеличением толщины составной пластины.

Таблица 3

Зависимость критической скорости от толщины квадратной составной пластины

Dependence of critical velocity from the thickness of square combined plate

Table 3

Параметр	Значение
h/b	0,005	0,006	0,007	0,008	0,009	0,01
U / c 0	1,08	1,84	2,91	4,33	6,16	8,45

В качестве второго примера рассмотрим удлиненную составную пластину «сталь – алюминий» (сталь – р = 7,8 - 10 3 кг/м³, E = 1,9982 - 10¹¹ Па, v = 0,3, алюминий - р = 2,75 - 10³ кг/м³, E = 0,7 - 10¹¹ Па, v = 0,34), изображенную на рис. 6, асимметричную относительно начала координат. Заметим, что для данной пластины сходи-

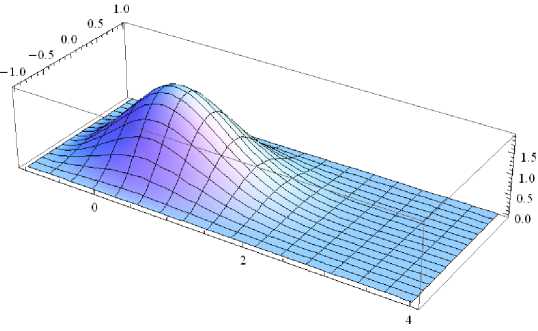
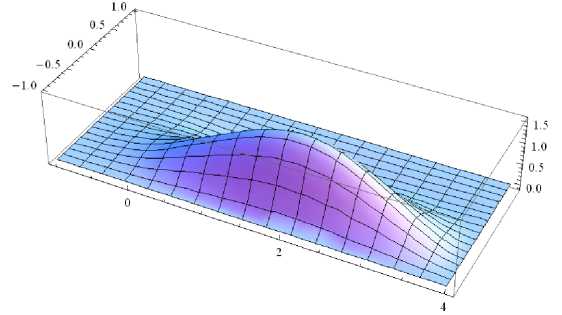
b

Рис. 7. Формы потери устойчивости составной удлиненной пластины сталь – алюминий: a – U ₀ = 23,44; b – U ₀ = 67,08

Fig. 7. Buckling forms for the long combined plate steel – aluminum: a – U 0 = 23,44; b – U 0 = 67,08

Опять вспучивание происходит в той части пластины, которая расположена против вектора потока. При этом более жесткая стальная вставка в левой части пластины приводит к тому, что эта часть оказывается менее вспученной: так, на рис. 7, b , этот факт иллюстрируется наиболее отчетливо, можно увидеть, что эта часть пластины имеет малые прогибы.

В табл. 4 представлена зависимость критической скорости потери устойчивости от безразмерной толщины h / b для удлиненной пластины, изображенной на рис. 6. Аналогично предыдущему случаю квадратной пластины можно увидеть, что с увеличением толщины критическая скорость быстро возрастает, оставаясь при этом меньше соответствующих значений для составной квадратной пластины.

Таблица 4

Зависимость критической скорости от толщины удлиненной составной пластины

Dependence of critical velocity from the thickness of long combined plate

Table 4

Параметр	Значение
h/b	0,0065	0,007	0,008	0,009	0,01
U / c 0	1,16	1,44	2,15	3,04	4,17

Заключение

Таким образом, в статье на основе метода спектральной динамической жесткости впервые предлагается алгоритм исследования динамической устойчивости составных пластин в потоке газа. Представлены