Метод стохастической оптимизации логистической инфраструктуры

Сущность ПСМ состоит в том, что движение к оптимуму в k-мерном пространстве управляемых переменных x i осуществляется последовательным отражением вершин симплекса. В k-мерном евклидовом пространстве k-мерный симплекс представляет собой фигуру, образованную k+1 точками (вершинами).

В одномерном пространстве симплекс есть отрезок прямой, в двумерном – треугольник, в трехмерном – тетраэдр. В ПСМ используются регулярные симплексы (расстояния между вершинами равны). Алгоритм перемещения симплекса в сторону цели состоит в зеркальном отражении вершины с наихудшим значением целевой функции. Например, при поиске максимума целевой функции целесообразно движение от вершины V s с наименьшим значением W к противоположной грани симплекса. Важное преимущество симплексного поиска перед другими методами состоит в том, что на каждый шаг требуется всего одно измерение целевой функции W, что значительно повышает эффективность поисковой оптимизации.

Вместе с тем постоянный размер симплекса не обеспечивает одновременно высокую скорость движения симплекса в начале поиска и точность отыскания экстремума на заключительном этапе оптимизации. Поэтому для достижения быстрого и точного решения требуется измерение размеров симплекса в процессе поиска. Деформация симплекса предусматривает сокращение или увеличение расстояния L между его вершинами с сохранением одной из них. В качестве последней можно выбрать вновь полученную вершину, либо вершину с наилучшим значением целевой функции y. При этом размеры ребер симплекса в процессе поиска определяются следующей зависимостью:

L n =L 0 * y n , (1) где n –номер шага;

y n – числовая последовательность, определяющая закон изменения шага.

Важно помнить о том, что шаги симплекса за пределы факторного пространства и в обратном направлении запрещены.

ПСМ является достаточно эффективной оптимизационной процедурой для широкого класса задач, связанных с поиском минимума/максимума унимодальных функций. В задачах глобальной оптимизации ПСМ приходится использовать многократно, каждый раз изменяя координаты центра начального симплекса. Эффективность глобальной оптимизации в ряде случаев может быть существенно увеличена, если процедуре

ПСМ придать свойства так называемого "случайного поиска".

Рассмотрим данный метод на конкретной задаче.

В регионе имеются три карьера природного сырья. Для освоения данных месторождений планируется построить горный обрабатывающий комбинат (ГОК). Координаты карьеров следующие: К 1 (10;90), К 2 (90;10), К 3 (80;80).

Стоимость перевозки 1 тонны сырья на 1 километр составляет: для первого карьера – 500 у.е., для второго – 600 у.е. и для третьего – 700 у.е.

Требуется выбрать оптимальное место для строительства ГОК, обеспечив минимум транспортных издержек.

В качестве целевой функции воспользуемся выражением:

w =500∙ у/ ( Xk 1- X гок) ²+( Yk 1- Y гок) ²

+

+ 600∙ ^j ( Xk 2- X гок) ²+( Yk 2- Y гок) ²

+

+ 700∙v( Xk 3- X гок) ²+( Y к 3- Y гок) ² (2)

В системе координат XY изобразим исходный симплекс со стороной в 15 км и

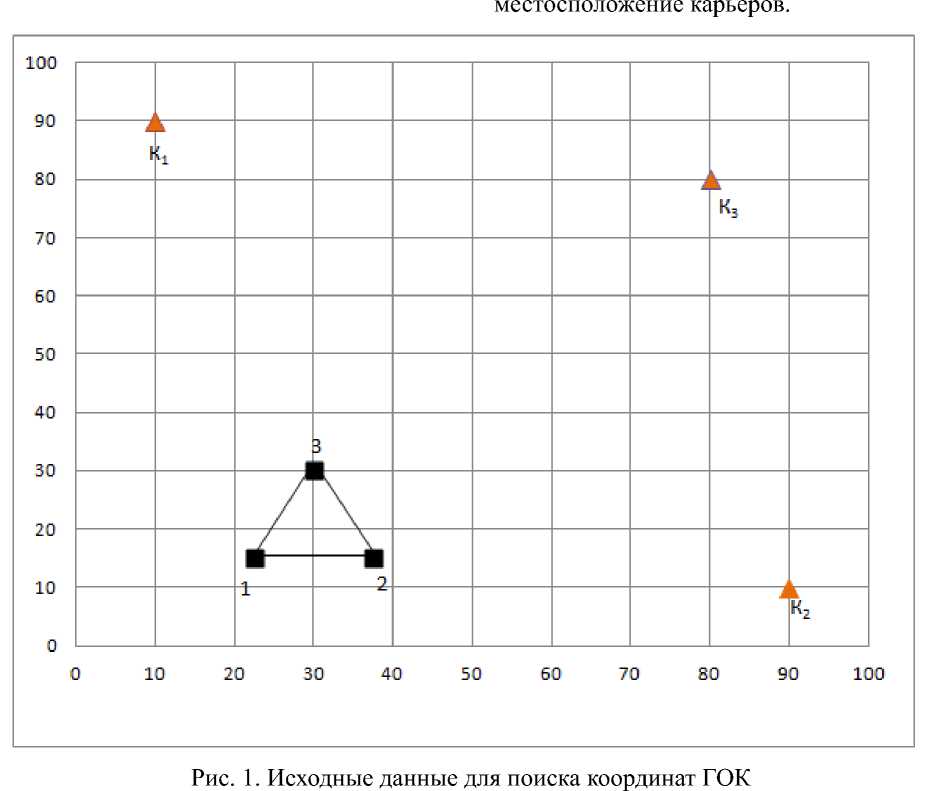
Алгоритм метода:

• 1.    Рассчитаем W для трёх вершин начального симплекса.

• 2.    Найдем сумму W1, W2, W3.

• 3.    Найдем р 1 , р 2 , р 3 :

• 4.    На отрезке числовой оси отметим

• 5.    С помощью генератора случайных чисел (ГСЧ) получаем число α є R (0;1), отмечаем его на отрезке числовой оси. В зависимости от того, в какой из трех образовавшихся интервалов 1, 2 и 3

р i = W i / ∑W j ; j= 1,3.                   (3)

значения р 1 и (р 1 + р 2 ) в интервале от 0 до 1.

попадет число, ту вершину и отражаем.

Оптимальным    месторасположением

ГОК является вершина, в которой значение W окажется минимальным в последнем симплексе.

Траектория поисковой оптимизации для n = 4 шагов представлена на рис. 2.

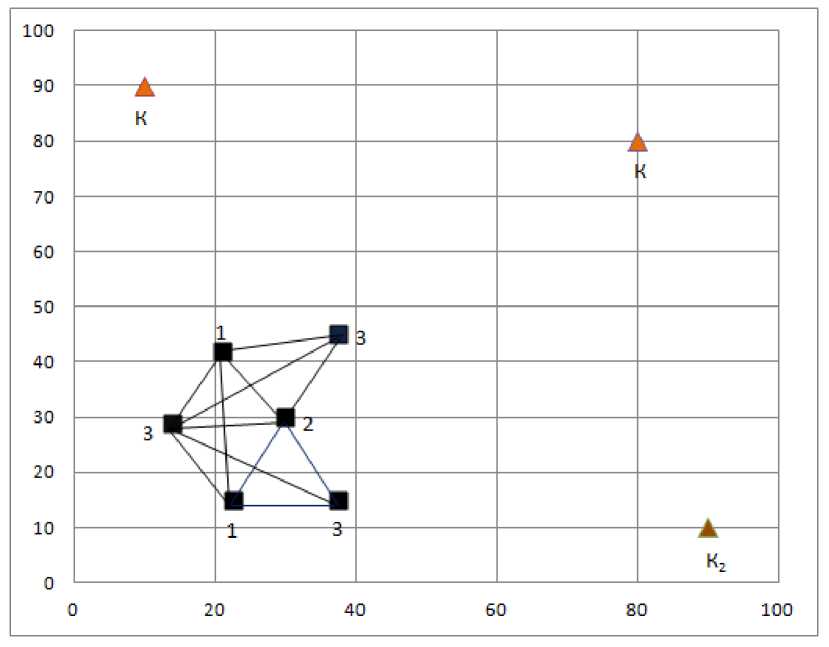
Рис. 2. Пример последовательного симплекса метода в режиме стохастической оптимизации

Таким образом, нами рассмотрена методика стохастической оптимизации логистической инфраструктуры, которая является универсальной и обладает, согласно закону больших чисел, вероятностной сходимостью к правильному результату.