Метод структурирования монотонно изменяющихся непрерывных функций на примере процессов АПК

Введение. Многие процессы в различных областях естественных наук описывают монотонно изменяющимися функциями [1–3]. Зачастую возникает необходимость их структурирования, когда в зависимости от варьирования аргумента функция изменяется наиболее интенсивно (существенно), менее интенсив- но (малосущественно) и с незначительной интенсивностью (несущественно).

Существует ряд способов, методов и приемов процедуры структурирования массива теоретических и экспериментальных данных, в том числе и авторами данной статьи. Так, в [4] использо- вали математический метод структурирования массива данных по анализу интегральной функции накопленных частот доли каждого фактора, но для дискретной функции.

В работе [5] нами предложен и реализован метод определения критической точки асимптотически изменяющейся (монотонно возрастающей) непрерывной зависимости, основанный на сравнении частного приращения искомой функции на каждом единичном интервале аргумента относительно гипотетической прямой со средним гипотетическим приращением на всем интервале изменения функции.

Такой подход позволяет определить критическую точку изменения функции только на границе выбранного единичного интервала аргумента, тогда как на практике критическая точка будет находиться часто в пределах единичного интервала (слева или справа). С этим связан ряд недостатков (неточностей) при определении координат критической точки, а на начальном этапе структуризации границы между существенной и малосущественной зонами.

Цель исследований: разработка метода структурирования монотонно изменяющихся функций (теоретических или экспериментальных после аппроксимации) и апробация его на примерах процессов АПК.

Материалы и методы исследования. Пусть функция f(x) непрерывна в интервале аргумента [x1; x2] и дифференцируема во всех внутренних точках этого интервала. Рассмотрим монотонно изменяющуюся непрерывную функцию (рисунок 1), определенную в интервале [x1; x2]. Согласно теореме Лагранжа [6] на интервале [x1; x2] найдется хотя бы одна точка (С), для которой справедливо равенство fM-fM-fW-^-xO. (1)

В графической интерпретации (рисунок 1) точка C – это точка, через которую проходит касательная А 1 В 1 к графику функции f ( x ), параллельная отрезку АВ , соединяющему точки графика с абсциссами x 1 и x 2 .

Рассматривая схему, представленную на рисунке 1, согласно методу, критической можно считать точку С , поскольку для последующей за ней точкой В выполняется условие

Δ y i +1 < Δ y ,

где среднее гипотетическое Δ y определяется как

A y =

^y max   y min

n

Точка С ограничивает область существования функции, где она изменяется существенно – это интервал [ x 1 ; x С ].

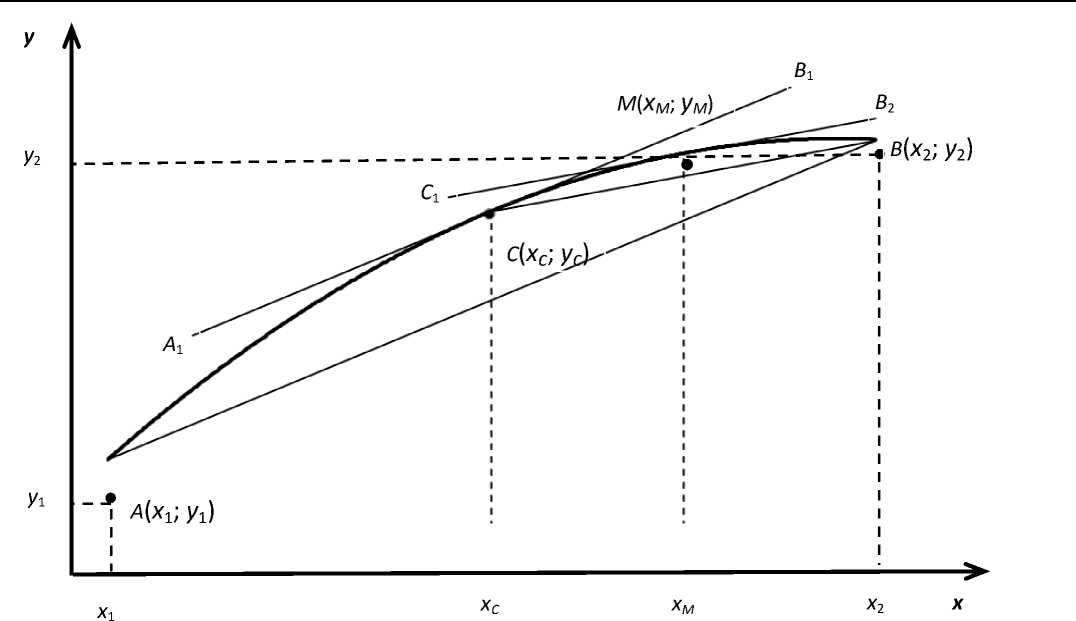
Рисунок 1 – Схема к определению критических точек изменения монотонно изменяющейся функции Figure 1 – Scheme for determining critical points of changing a monotonically changing function

Применив вышеописанный прием и теорему Лагранжа для интервала [xС; x2], можно аналогично определить точку среднего темпа изменения функции на этом интервале и получить точку М, проведя касательную С1В2 к графику функции f(x) на интервале [xС; x2], параллельную отрезку СВ, таким образом выделив интервал [xC; xM], где функция изменяется малосущественно, и интервал [xM; x2], где функция изменяется несущественно. Эти точки можно получить и теоретически после следующих рассуждений (рисунок 2). После ввода в разработанный в соответствии с [7, 8] алгоритм формулы или эмпирической зависимости, описывающей монотонно изменяющуюся функцию (блок 1, да), выбирают интервал или определяют изменения аргумента (блок 2). В случае их отсутствия (блок 1, нет), вводят массив экспериментальных данных {yi} (блок 3) и после их аппроксимации (блок 4) направляют для выбора или определения интервала изменения аргумента (блок 2). По полученной эмпирической зависимости или имеющейся формуле производят совместное их решение и с учетом выбранного интервала изменения аргумента находят интервал изменения функции (блок 5). Далее находят угловой коэффициент "существенности" (блок 6). Определяют первую производную искомой функции y′ (блок 7) и после её совместного решения с выражением для углового коэффициента "существенности" находят значение аргумента существенности (блок 8).

После подстановки в формулу или эмпирическую зависимость аргумента "существенности" (блок 9) устанавливают ординату "существенности" y c . С учетом значений аргумента и ординаты "существенности" рассчитывают угловой коэффициент «малосущественности» (блок 10).

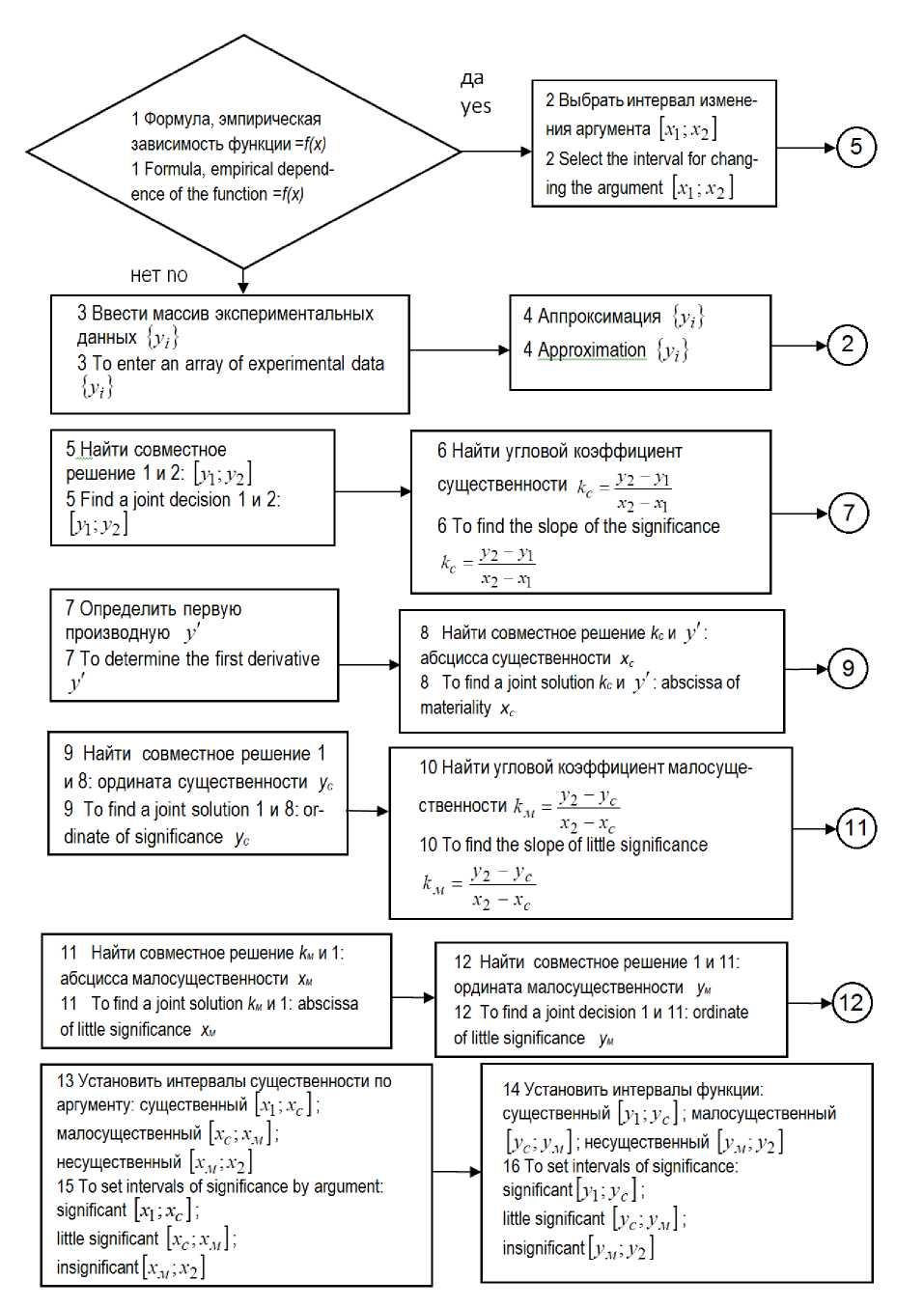
Рисунок 2 – Алгоритм определения граничных точек при структурировании монотонно изменяющейся функции

Figure 2 – Algorithm for determining boundary points when structuring a monotonically changing function

Решая совместно выражения для первой производной функции и углового коэффициента "малосущественности", определяют (блок 11) аргумент "малосу-щественности" и после подстановки его значения в формулу или эмпирическую зависимость находят значения ординаты "малосущественности" (блок 12). Далее устанавливают интервалы существенного, малосущественного и несущественного изменения аргумента (блок 13) и функции (блок 14).

Результаты исследования и их обсуждение. Практически метод был реализован по данным расчетов (таблица) при реализации вышеописанного алгоритма на примере определений полного сопротивления кормосмеси постоянному току от длительности замера (рисунок 3) как разделяющего признака при определении показателя неравномерности смешивания [9–11] ингредиентов зимнего кормового рациона для свиней на откорме.

Результаты расчета критических точек монотонно изменяющихся функций Results of calculation of critical points of monotonically changing functions

№ п/п	Поблоковая реализация алгоритма Block-by-block implementation of the algorithm	Номер рисунка Figure number
		1	2	3
1	[ x 1 ; x 2 ]	[0; 270]	[1,35; 17,22]	[0,5; 10]
2	[ y 1 ; y 2 ] (совместное решение (2) и (4)) [ y 1 ; y 2 ] (joint decision (2) и (4))	[1526,2; 2168,3]	[0,6213; 0,2867]	[51,6981; 13,3878]
3	Эмпирическая зависимость, f = y(x) Empirical dependence, f = y(x)	0,0098τ²+5,0242τ+ +1526,2	0,0016P2-0,0508P+ +0,687	37,819 V -0,451
4	Первая производная эмпирической зависимости, f ′ ( x ) First derivative of empirical dependence, f ′ ( x )	-0,0196τ+5,024	0,0032P-0,0508	- 17,0564 V -1,451
5	Угловой коэффициент, y 2 - y 1 x 2 - x 1 Slope, y 2- y 1 x 2 - x 1	2,3782	-0,0211	-4,0327
6	х с , совместное решение (5) и (6) х с , joint decision (5) и (6)	135	9,285	2,7702
7	y c , совместное решение (4) и (7) y s , joint decison (4) и (7)	2025,862	0,3533	24,1571
8	Угловой коэффициент, y 2 - y c x 2 - xc Slope, y 2 - y c x 2 - xc	1,0552	-0,0084	-1,4756
9	х м , совместное решение (5) и (9) х m , joint decision (5) и (9)	202,5	13,2525	5,4019
10	y м , совместное решение (4) и (10) y m , joint decision (4) и (10)	2141,739	0,2948	17,6739

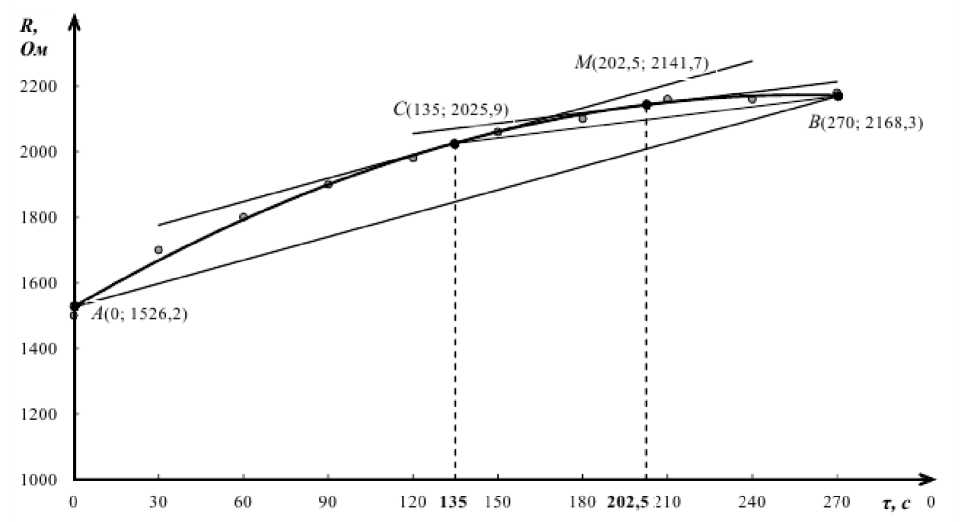
Рисунок 3 – Зависимость полного сопротивления кормосмесей постоянному току от длительности замера для алюминиевых электродов и относительной влажности кормосмеси 72,31%

Figure 3 – Dependence of the total resistance of feed mixtures to direct current on the duration of the measurement for aluminum electrodes and relative humidity of the feed mixture of 72.31%

При этом установили, что наиболее существенно значение функции изменяется до 135 с, малосущественно от 135 до 202,5 с и далее изменение идет несущественно. Это дает основание с большой долей вероятности и для удобства пользования фиксировать значение разделяющего признака в течение 150 с.

Далее при исследовании влияния вертикальной нагрузки в пределах от 0,78 до 16,67 кПа на коэффициент трения по стали, определенный в соответствии с [12, 13], кормовой свеклы влажностью 88,34% и средней степени измельчения 5,45 мм, установили (рисунок 4) следующее. С ростом вертикальной нагрузки до 9,29 кПа происходит относительно существенное изменение коэффициента внешнего трения от 0,62 до 0,35, далее при нагрузке от 9,29 до 13,25 кПа темп изменения не является существененным и находится в пределах [0,35; 0,29]. Таким образом, можно утверждать, что для практических расчетов следует учитывать изменение коэффициента внутреннего трения кукурузного силоса при вертикальном давлении до 13,25 кПа, используя полученную после аппроксимации зависимость, а с увеличением вертикальной нагрузки выше этого значения использовать значение коэффициента трения, соответствующее этой нагрузке, то есть 0,35.

Следующая реализация предлагаемого метода осуществлена (рисунок 5) при определении оптимального значения полезной вместимости порционного циркуляционного смесителя кормов для приготовления запариваемой кормосмеси для свинопоголовья с учетом методических положений, изложенных в [14, 15].

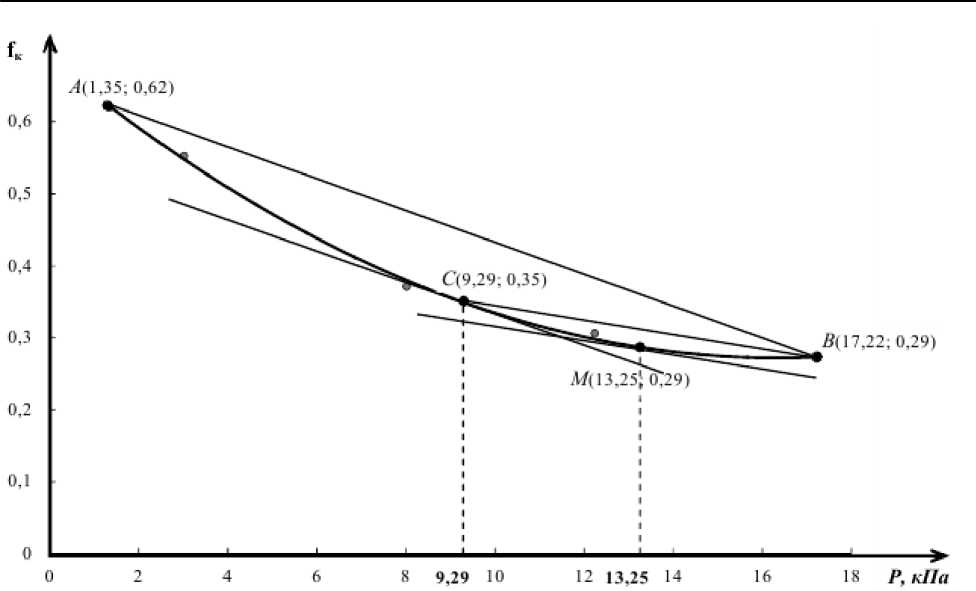
Рисунок 4 – Зависимость коэффициента внешнего трения по стали свеклы кормовой (средняя длина частиц 5,45 мм, относительная влажность 88,34%) от поверхностной нагрузки Figure 4 – Dependence of the coefficient of steel external friction on fodder beet (average particle length 5.45 mm, relative humidity 88.34%) on the surface load

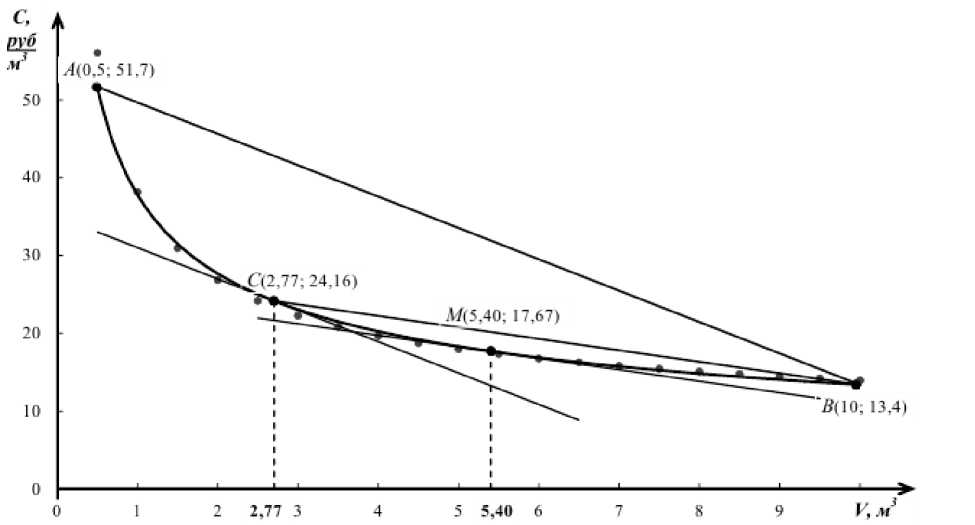
Рисунок 5 – Зависимость удельной стоимости запаривания кормосмеси для свиней от полезной вместимости порционного смесителя кормов при их суточной потребности 100 м3 Figure 5 – Dependence of the specific cost of steamed feed mixture for pigs on the useful capacity of a portioned feed mixer with a daily requirement of 100 m3

Выводы

• 1.    На основании теоремы Лагранжа разработан метод структурирования монотонно изменяющихся непрерывных функций, определяющий координаты точек существенности и малосущественно-сти в графической интерпретации как точки касания соответственно: прямой, параллельной отрезку, соединяющему начальную и конечную точки интервала задания функции (точка существенности) и прямой, параллельной отрезку, соединяющему точку существенности и конечную точку интервала задания функции (точка малосущественности).

• 2.    Разработан и представлен алгоритм реализации метода.

• 3.    Алгоритм реализован при исследовании ряда технологических процессов в отраслях животноводства АПК. Так:

  – значение полного сопротивления кормосмеси постоянному току от длительности замера наиболее существенно изменяется до 135 с, менее существенно от 135 до 202,5 с, а далее несущественно, что дало основание фиксировать этот разделительный признак через 150 с;

  – коэффициент трения по стали кормовой свеклы, измельченной до среднего размера 5,45 мм и относительной влажностью 88,34% при значении удельной вертикальной нагрузки до 9,29 кПа снижается наиболее резко (от 0,62 до 0,35), а при значении от 9,29 кПа до13,25 кПа менее резко (от 0,35 до 0,29). Это дает основание при практических расчетах принимать значение коэффициента трения при вертикальной нагрузке свыше 13,25 кПа от 0,35 до 0,29;

  – себестоимость приготовления

• 1    м³ кормосмеси для свинопоголовья в порционном смесителе наиболее заметно снижается с ростом его полезной вместимости до 2,77 м³, а далее до 5,40 м³ не дает значительного экономического

эффекта, что дает основание выбирать величину полезной вместимости в пределах до 2,77 м3.