Метод сжатия изображений для беспроводной капсульной эндоскопии

Данная статья посвящена вопросам сжатия изображений без потери качества в целях последующей передачи по специальному каналу для использования в перспективном направлении медицинских исследований – беспроводной капсульной эндоскопии. Так как в процессе диагностики желудочно-кишечного тракта пациента капсула производит два снимка в секунду, то к концу исследования накапливается более 57 тысяч изображений. После за- вершения исследования эти изображения передаются на стационарный компьютер, где происходит их дальнейшая обработка.

В системе беспроводной эндоскопии особенно остро стоит вопрос обеспечения достаточной мощности передатчика, длительности работы блока питания и размеров оборудования. Уменьшение передаваемой информации приведет к увеличению частоты получения изображений, снижению энергопотребле- ния, и, как следствие, – к более долгой работе эндоскопической капсулы. Таким образом, появляется задача сжатия изображений внутри капсулы, что позволит получить максимум данных для анализа, не увеличивая при этом размеры прибора.

Данные с камеры передаются в память, организованную в виде очереди по принципу FIFO (First In – First Out, первым пришел – первым ушел). Далее из памяти массив поступает на микросхе- му сжатия по однобитному порту. Цвет пикселя изображения определяется тремя составляющими по схеме RGB (Red, Green, Blue – красный, зеленый, синий). После чего данные сжимаются и отправляются по 8-битному порту на передатчик. Передатчик капсулы посылает кодовые слова на внешний приемник, который, в свою очередь, декодирует изображение.

Область применения устройства накладывает жесткие ограничения на схему сжатия:

• 1)    низкое энергопотребление – капсула работает на батарее, и высокое энергопотребление сократит время ее работы;

• 2)    массив памяти обновляется каждые 0,5 с – время сжатия не должно превышать этого ограничения;

• 3)    размеры капсулы составляют 1,5 – 2 см, что накладывает ограничение на размер микросхемы. Оптимальным вариантом станет размещение информации на кристалле размером 5×5 мм.

Для решения проблемы сжатия информации без потерь с учетом выдвигаемых требований к конечному устройству были выбраны следующие алгоритмы:

• 1)    кодирование тройками двоичных наборов (КТ);

• 2)    комбинация преобразования MTF (move-to-front – движение к началу) и кодирования Райса.

Кодирование тройками двоичных наборов

Кодирование тройками двоичных наборов относится к универсальному кодированию. Универсальное кодирование характеризуется тем, что статистическая избыточность в последовательности, полученной после кодирования, стремится к нулю с ростом длины блоков, на которые разбивается исходная бинарная последовательность.

Данный метод используется, когда требуется абсолютно точно восстановить исходную двоичную последовательность, а сжатие данных за счет потери части информации неприемлемо [1, 4, 5].

Исходная последовательность двоичных данных разбивается на блоки разрядностью n (n бит). Для каждого блока определяются три параметра, вычисляемые на основе его содержимого:

• 1)    количество единиц в блоке – k ;

• 2)    номер суммы их позиций – s ;

• 3)    номер данной конкретной комбинации в соответствующем классе (элемент пересечения множеств K и S ) – b(n,k,s) .

Доказано, что избыточность R_n в потоке выходных данных стремится к нулю с ростом длины исходных блоков n , т.е. кодирование является асимптотически оптимальным:

limR n = 0,                         (1)

где n → ∞ ; R_n – избыточность кодирования:

R n = sup R n (р) , где о < р < 1 ,

Rn(р) = nср/n – Н(р), где nср – средняя длина кодового слова, Н(р) = –(p log2p + q log2q) – энтропия источника.

Номер данной конкретной кодовой комбинации вычисляется по формуле,

b(n,k,s) = r(i k –1,k, i k + i k-1 +... + i 1 )+ + r(i k-1 – 1,k-1, i k-1 + i k-2 ...+i 1 )+… + r (i 2 – 1, 2, i 2 + i 1 ) = kj

- Z r(i j — i,j, 2 i m ) ,                  (2)

j '= 2                            m = 1

где i – номера позиций единиц в исходном блоке [1].

Для уменьшения трудоемкости реализации имеет смысл ввести адаптацию в КТ, т.е. добавить в кодовое слово дополнительный бит, содержащий указание на то, кодировать информацию или нет, в зависимости от количества единиц во входном блоке.

Комбинация преобразования MTF и кодирования Райса

MTF – это преобразование для кодирования данных (обычно потока байтов), разработанное для улучшения производительности энтропийного кодирования. Основной идеей преобразования является замена каждого входного символа его номером в специальном стэке – регистре недавно использованных символов. Последовательности идентичных символов, например, будут заменены оригинальным алгоритмом (начиная со второго символа) на последовательность нулей. Если же символ долго не появлялся во входной последовательности, он будет аналогичен большому числу. В ходе преобразования происходит замена последовательности входных символов на последовательность целых чисел. Если во входных данных было много локальных корреляций, то среди этих чисел будут преобладать небольшие, лучше сжимаемые энтропийным кодированием, чем исходные данные [2, 3]. Код Райса – это семейство двоичных префиксных кодов представления натуральных чисел и нуля. Коды различаются одним параметром k – количество битов, отводимых на мантиссу числа. Способ кодирования и декодирования зависит от значения параметра, так что он должен быть известен как передатчику, так и приемнику.

Кодируемое число в двоичном представлении разбивается на две части: k самых младших разрядов и все остальные от k -го и старше. Старшая часть кодируется унарным кодом, а младшая – записывается сразу следом за кодированной старшей частью. Для n -блока данный код представляется в ( n ⁄ m + k + 1 ) битами, где m = 2^k – некоторое выбранное число, являющееся степенью двойки [2].

В результате моделирования и тестирования разработанных устройств, реализующих работу алгоритмов кодирования тройками двоичных наборов, комбинации преобразования MTF и кодирования Райса, были исследованы зависимости размера выходного файла и длительности обработки от параметров кодирования. В качестве параметров КТ использовались наличие/отсутствие адаптации, а также, при наличии адаптации, различные минимальные количества единиц. По результатам тестирования были составлены табл. 1 и табл. 2 , в которых приняты следующие обозначения: k_min – минимальное значение. К_сж – коэффициент сжатия данных. t – число тактов в миллионах, КБ – килобайт.

В результате, было выбрано сжатие по методу КТ с приведенными выше параметрами по следующим причинам:

• 1)    КТ обрабатывает входной блок за меньшее количество тактов;

• 2)    КТ имеет больший коэффициент сжатия;

  Таблица 1. Зависимость коэффициента сжатия КТ от различных параметров

  n	t , млн. тактов	Размер, КБ	Адаптация	k min	К сж
  8	30,5	325	нет	-	0,94
  16	-	213	нет	-	1,44
  24	-	160	нет	-	1,92
  24	3,3	273	есть	2	1,12
  	3,7	267	есть	3	1,14
  	5,2	267	есть	4	1,14
  	11,2	267	есть	5	1,14
  	45,4	267	есть	6	1,14
  32	3,2	268	есть	2	1,15
  	3,5	264	есть	3	1,16
  	5,2	262	есть	4	1,17
  	15,5	260	есть	5	1,18
  	60,1	259	есть	6	1,19
  48	3,2	259	есть	3	1,19
  	3,6	255	есть	4	1,20
  	5,9	251	есть	5	1,22
  	15,35	249	есть	6	1,23
  64	80,5	254	есть	5	1,20
  128	8,4	255	есть	4	1,20
  256	12,6	256	есть	4	1,19
  512	24,1	259	есть	4	1,18

  
  

• 3)    для реализации КТ при длине блока в 48 бит требуется меньшее количество памяти.

Возможны следующие варианты реализации КТ:

• 1)    программный подход, при помощи ЭВМ;

• 2)    аппаратно-программный способ, при помощи одноплатного компьютера или при помощи ЭВМ на одном кристалле;

• 3)    разработка специализированного ус-

• тройства на основе создания оригинальной микросхемы, с использованием флэш-технологий.

С учетом специфики применения, наиболее перспективным представляется третий путь сжатия изображения без потерь. На вход микросхемы поступает бинарная последовательность со статистической избыточностью, а с выхода снимается последовательность, лишенная избыточности, т.е. обеспечивается сжатие данных.

На рис. 1 приведен алгоритм, реализующий КТ. Приняты следующие обозначения: k – количество единиц в исходном блоке; s – номер суммы позиций единиц в исходном блоке; b – номер данной конкретной кодовой комбинации для фиксированных значений k и s ; N , K , S – служебные параметры для вычисления номера b по формуле (2); r (n, k ,s) – количество двоичных комбинаций имеющих k единиц и сумму их позиций s в n -разрядном блоке; A(I) – одномерный массив анализируемых битов входного слова; I – служебный текущий индекс номеров позиций единиц.

Значение n считается заданным – длина блоков, на которые разбивается исходная последовательность двоичных символов (блок А1).

Под I понимается номер обрабатываемого разряда текущего n -блока; k – текущее значение количества единиц в блоке; S – сумма номеров их позиций; b – номер, вычисляемый по формуле (2); А(I) – содержимое I -го разряда n -блока. В блоках А2, А3, А4, А5 значениям параметров кодового слова присваиваются исходные значения.

Пусть с выхода канала поступают последовательно двоичные данные. В блоке А6 осуществляется прием очередного бита этой последовательности. В блоке А7 значение I увеличивается на единицу.

В блоке А 8 определяется, равно ли содержимое I -го разряда n -блока единице, и, если «да», то происходит вычисление соответствующего слагаемого формулы (2) номера кодовой комбинации (блоки А9, В1,2,3). В блоке В4 вычисленное слагаемое прибавляется к текущему значению номера b .

Если в блоке А8 выясняется, что содержимое I -го разряда n -блока равно нулю, то происходит переход на блок В5. Здесь выявляется, все ли разряды n -блока проверены, и, если «нет», то

Таблица 2. Зависимость коэффициента сжатия кодированием Райса от разных параметров сжатия

k min	2	3	4	5	6	2	3	4	5	6
Ксж	0,50	0,78	0,98	1,11	1,09	0,73	1,04	1,21	1,21	1,12
Размер, КБ	612	392	302	275	281	415	295	254	254	274
t , млн. тактов	1,8					23
MTF	нет					есть

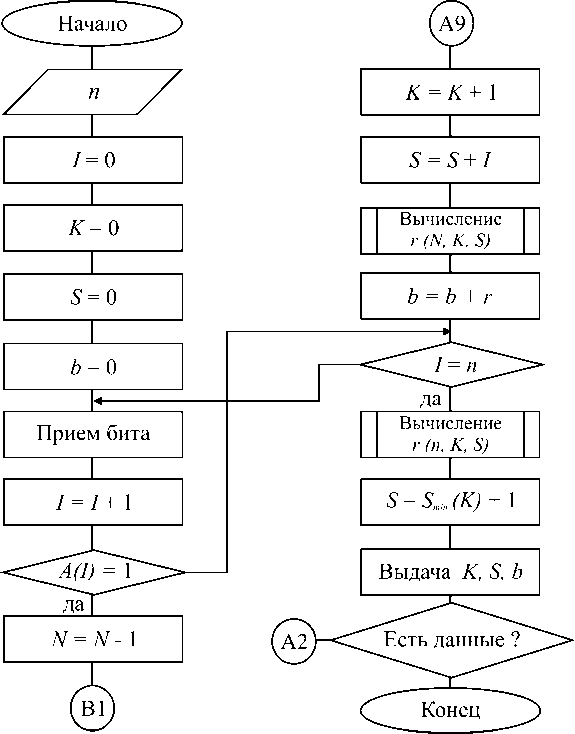
Рис. 1. Алгоритм кодирования

осуществляется переход на блок А6. Если «да», то в блоке В6 происходит модификация значения суммы позиций единиц исходного блока, т.е. осуществляется замена исходного значения S , на его номер.

В блоке В7 вычисляется коэффициент, необходимый для определения количества разрядов, требуемых для номера передаваемой кодовой комбинации. В блоке В8 происходят выдача сформированного кодового слова. Если по завершению передачи очередного кодового слова из канала продолжают поступать данные, осуществляется переход на блок А2.

Реализованное по итогам исследования устройство производит сжатие получаемых эндоскопической капсулой изображений без потерь примерно на 20% в реальном времени. При этом соблюдаются все технические требования, выдвигаемые к беспроводному эндоскопу.

В сочетании с программным обеспечением, установленным на приемнике, которое автоматически отбирает изображения, пригодные для исследования, разработанный метод позволяет получить наиболее полную картину ЖКТ пациента в удобной для анализа форме ■