Метод сжатия модели машинного обучения на основе итеративной фильтрации слоев

Развитие моделей машинного обучения привело к значительному росту количества модулей, слоев и числа обучаемых весов, что требует масштабной инфраструктуры для их функционирования касательно вычислительных операций и использования памяти. Современные модели могут включать миллиард [1,2] или более [3,4] обучаемых параметров, что делает невозможным их использование на компактных устройствах, таких, как портативные компьютеры или смартфоны.

Помимо запуска моделей машинного обучения на небольших устройствах, часто возникает задача их дообучения [5] под конкретные задачи, что также становится затруднительно из-за внушительного количества весов, ввиду необходимости хранения тензоров рассчитываемых градиентов и еще большего расхода памяти.

Одним из методов снижения сложности вычислений, а также сокращения количества параметров при сжатии модели является урезание весов в соответствии с заданными правилами (weight pruning - в англоязычной литературе) [6].

В данном исследовании рассматривается один из вариантов метода сжатия модели за счет фильтрации весов. Основной идеей метода является такая особенность моделей, как приведение обучаемых параметров к нормальной плотности распределения за счет повсеместного применения слоев нормализации [7]. В качестве критерия удаления (1) весов использовались интервалы среднеквадратичного отклонения шириной: один-сигма, два-сигмы и три-сигмы нормального распределения с последующим применением (2) масштабирующего коэффициента к оставшимся весам урезанных слоев (рис. 1).

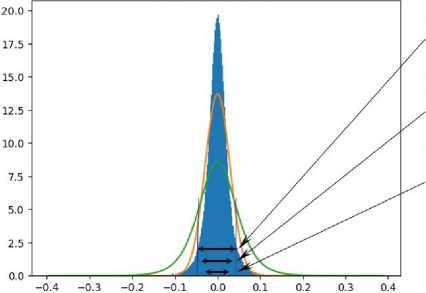
Ширина интервала три сигмы: [-0.0872, 0.0873]

Ширина интервала два сигмы: [-0.0581,0.0582]

Ширина интервала один сигма: [-0.0290, 0.0291]

Рис. 1. Пример распределения весов для произвольного слоя модели машинного обучения па базе архитектуры трансформера

Применение метода сжатия к слоям осуществлялось на основе итеративного алгоритма с получением промежуточных оценок качества (метрик). Помимо этого, был проведен (3) анализ зависимости обработанных слоев от параметров сжатия.

Процесс итеративного удаления весов по слоям с последующим масштабированием схематично представлен на рис. 2.

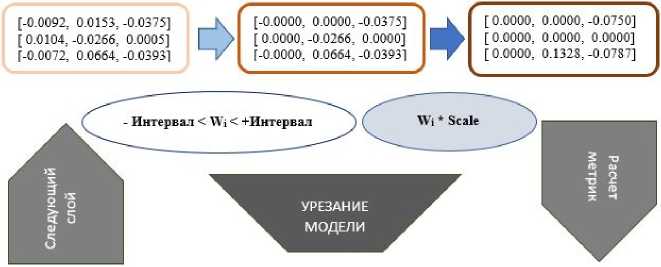
Рис. 2. Схема итеративного удаления и масштабирования параметров модели машинного обучения

Ввиду значительных ограничений вычислительных мощностей аппаратных средств (8GB RTX NVIDIA 4060М) для исследований была использована небольшая языковая модель «bert-base-uncase» размером ПО миллионов параметров, дообученная под задачи классификации текста.

2.    Обзор современных подходов к сжатию моделей машинного обучения посредством урезания весов

На сегодняшний день опубликовано несколько сотен научных работ, связанных с удалением модулей, слоев и весов моделей машинного обучения. Причем количество публикаций увеличивается по мере роста количества параметров [9], что подчеркивает актуальность исследований, связанных с сжатием и снижением количества вычислительных операций при использовании больших моделей.

Исходя из анализа ранее проведенных исследований, можно сделать вывод, что удаление элементов модели возможно осуществить несколькими способами: структурно, то есть, когда вырезаются полностью модули или слои [10], используя удаление параметров вне зависимости от структуры модели из всех или некоторых слоев, а также смешанным способом [11].

Немаловажным вопросом является: на каком этапе следует осуществлять фильтрацию весов. В частности, урезание может проводится перед обучением за счет случайной начальной инициализации весов и их дальнейшим удалением по выбранному критерию [12]. Помимо этого, веса могут удаляться в процессе обучения совместно с расчетом функции потерь, что позволяет настраивать модель параллельно с вычислением обратного распространения ошибки. Кроме того, удаление весов может осуществляться после завершения обучения модели [13].

В зависимости от этапа удаления могут применяться различные критерии урезания, как весов, так и слоев в целом. Некоторые методы в качестве оценки значимости весов используют рассчитанный градиент [14], величину веса, метрики расстояния и разреженность тензоров [15,16].

На основе используемого критерия сам процесс урезания может проходить итеративно по всей модели, постепенно или единожды. Итеративное удаление в значительной мере «завязано» на имеющиеся вычислительные мощности, так как периодическая обработка даже не всех весов в больших моделях может потребовать длительных расчетов.

Также удаление слоев и параметров модели используется для усиления других методов компрессии и дообучения подобно квантованию, адаптации с использованием низкоранговых тензоров и т. п. [17,18].

В данном исследовании рассматривается итерационный метод сжатия обученной модели на основе фильтрации слоев посредством урезания и масштабирования параметров по предлагаемому критерию. Разработанный метод обладает рядом преимуществ:

• -    инвариантность к архитектуре модели;

• -    итеративность удаления весов по слоям дает возможность последовательно оценивать промежуточный результат и при необходимости возвращаться на шаг назад;

• -    гибкость настройки фильтрации и возможность подбора наилучших параметров сжатия;

• -    связь критерия урезания весов непосредственно с особенностями функционирования модели - нормализации весов;

• -    возможность оценки качества обученной модели по нескольким хорошо известным метрикам, что позволяет в дальнейшем использовать их как условия для контроля результатов удаления параметров из выбранных слоев.

• 3.    Метод сжатия на основе итеративной фильтрации слоев

  3.1.    Критерий фильтрации параметров в слоях модели

Фильтрация значений на базе определенных критериев позволяет рационально урезать веса в слоях модели посредством чего осуществляется ее сжатие.

Одним из первых критериев фильтрации использовался порог в качестве правила для удаления весов [19]. В предлагаемом методе также применяется порог, который основывается на следствии от повсеместного применения послойной нормализации весов в модели.

Нормализация по слоям способствует повышению стабильности функционирования моделей машинного обучения за счет сведения весов к нулевому математическому ожиданию и единичной дисперсии. Это приводит к тому, что распределение весов в слоях модели стремится к аналогу нормального распределения [20] (рис. 1).

Основываясь на данном факте в качестве критериев для удаления весов, были приняты интервалы, соответствующие количеству среднеквадратичных отклонений нормальной плотности распределения. Помимо удаления весов, попадающих в указанные интервалы, предлагается умножать значения оставшихся весов на масштабирующий коэффициент, полученный опытным путем.

Подобный механизм нейронного взаимодействия реализован в живой природе, где при обучении формируется множество связей, которые могут быть как необходимыми для закрепления знаний, так и нет, что может привести к их разрушению со временем. В свою очередь важные связи с повторением знания усиливаются, тем самым закрепляя полученный опыт [21].

Предварительное воздействие масштабирующего коэффициента на параметры и в целом функциональность модели было рассмотрено на примере относительно небольшой сверточной сети (около 25 млн параметров) ResNet-50 [22], решающей задачу классификации объектов. Для удаления и умножения на масштабирующий коэффициент параметров в архитектуре ResNet-50 был выбран последний полносвязный слой.

В качестве входных данных использовались несколько изображений из сети «Интернет» (рис. 3), которые отсутствуют в стандартном датасете ImageNetlOOO, но присутствуют, как прогнозируемые классы («tabby cat - 281», «tiger cat - 282», «Egyptian cat - 285»).

При предварительном испытании метода использованы следующие параметры сжатия: sigma = 1, scale = 1.5 и 2. Компрессия слоя при данных параметрах составила около 69%.

В результате применения двукратного масштабирования к слою с урезанными весами заметно возросло (с 4% до 40%) значение вероятности классификации (таблица 1) по сравнению с оригинальной сетью, не подвергавшейся воздействию. Также изменились некоторые классы изображений (3,4) вне зависимости от коэффициента масштабирования, однако данные классы остаются очень близки друг к другу.

Рис. 3. Изображения, используемые для анализа результатов масштабирования

Таблица!

Результаты удаления и масштабирования весов сети «ResNet-50»

	Оригинальная сеть		sigma = 1, scale = 1.5		sigma = 1, scale = 2
№	Класс	Вероятность	Класс	Вероятность	Класс	Вероятность
1.	282	0.5391	282	0.5116	282	0.5663
2.	282	0.5289	282	0.4884	282	0.6893
3.	281	0.5777	285	0.6671	285	0.7682
4.	281	0.5222	282	0.4512	282	0.5596
5.	281	0.8382	281	0.6858	281	0.7800
6.	282	0.7299	282	0.6792	282	0.8284
7.	285	0.5914	285	0.9117	285	0.9703

3.2.    Постановка задачи сжатия модели машинного обучения

На основе предлагаемой методики сжатия была поставлена задача поиска урезанной модели машинного обучения.

Заданы входные данные X = {х1,х₂, ... ,x_n} С D, (D - датасет) которые подаются на вход модели f(*). результатом которой являтотея выходные значения у С Y'.

У = f (X х W) ,

где W - веса модели.

После применения метода сжатия слоев необходимо найти такую модель, которая удовлетворяет ряду метрик с допустимым уровнем снижения:

у = f (х х W*\Metrics > Metrics х dl^ ,

где W* - параметры модели, к которым применялось урезание и масштабирование, Metrics - метрики сжатой модели,

Metrics - метрики, используемые для контроля урезания слоев (эталонные), dl - допустимый уровень снижения метрик (в расчетах использовалось 0.95).

Для поиска модели требуется подобрать такие параметры сжатия: sigma, scale, чтобы:

у = minf (X х (W > sigma) * scale) , w где sigma - значение интервала среднеквадратичного отклонения (от 1 до 3). scale - коэффициент масштабирования весов.

3.3.    Итерационный алгоритм сжатия слоев обученной модели

Для поиска модели, удовлетворяющей (3), разработан итерационный алгоритм сжатия слоев, где входивши данными являются: параметры метода ( sigma, scale), слои (LAYERS), а также сэмплы (X ) из датасета (D) для промежуточного расчета метрик.

Псевдокод алгоритма сжатия слоев представлен в виде алгоритма 1.

Алгоритм 1 Итерационный алгоритм сжатия слоев модели

Require: X С D, layer С LAYERS, s'igma, scale

Ensure: W * С W

• 1:    for layer = 1 tо LAYERS do

• 2:       scale = [1 ... scale]

• 3:      sigma = [1 .. .a]

• 4:     layrr.W ^ layer.W > compute—interval(sigma)

• 5:     layer.W ^ layer.W x scale

• 6:     compute current _metrics(x)

• 7:    if current_met^rrics > original_metrics x decrease_level then

• 8:        layer.W * = layer.W

• 9:        layer.W * = layer.W

• 10:     end if

• 11:    end for

• 4.    Эксперимент

  4.1.    Используемая модель машинного обучения

Результатом работы алгоритма являются модели с разным уровнем сжатия, но допустимым уровнем отклонения от выбранных метрик. После расчета моделей также возможно оценить, как менялись слои в зависимости от исходных данных и какое количество весов от общего значения было удалено.

Для проведения эксперимента была использована модель на базе архитектуры трансформера, в частности «bert-base-uncased» [23], представленная в библиотеке transformers сервиса «huggingface». Данная модель была выбрана по ряду причин:

• -    на текущей момент это одна из наиболее популярных архитектур построения моделей;

• -    модель хорошо зарекомендовала себя для небольших задач (порядка 84 млн скачива-ний с сервиса);

• -    ограничения по вычислительной мощности (8 GB Nvdia RTX 4060М).

Структура модели включает в себя:

• -    модуль эмбеддинга из 5 слоев;

• -    12 блоков энкодера, каждый из которых состоит из 16 слоев различного типа;

• -    4 полносвязных слоя.

4.2.    Дообучение и применяемые метрики

Общее количество слоев, которое возможно обработать, составляет 201. Помимо слоев весов, также будут сжиматься слои смещения.

В связи с тем, что по современным меркам модель имеет достаточно малый размер (порядка ПО млн параметров) для подачи на её вход современных датасетов и расчета на их основе метрик, было осуществлено ее дообучение для решения задач бинарной классификации на датасете «imdbstfd».

В качестве оценки качества бинарной классификации были использованы хорошо зарекомендовавшие себя метрики: точноств (precision), полнота (recall), совпадение (accuracy), Fl и ROC_AUC кривая.

Расчет метрик на тестовой выборке представлен в табл. 2 и на рис. 4.

Т а б л и ц а 2

Метрики дообученной модели

Метрика	Значение для 40 сэмплов	Значение для 400 сэмплов
Accuracy	0.825	0.8175
ROC AUG score _ _	0.936	0.920
Fl-score	0.787	0.817
Precision	0.812	0.788
Recall	0.764	0.849

В целях экономии вычислительных ресурсов расчет метрик при работе итеративного алгоритма сжатия выполнялся на 40 сэмплах. Чтобы убедиться, что такого количества достаточно, были оценены метрики для 400 сэмплов, которые отклоняются в интервале от 0.9% до 9.8% от варианта с 40 сэмплами.

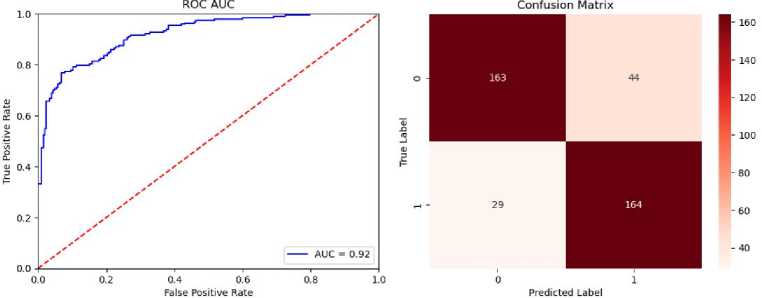
Рис. 4. ROC кривая и матрица ошибок для тестовой выборки из 400 сэмплов

Полученные значения метрик использовались в алгоритме как эталонные, и на их ос нове принималось решение при удалении весов из слоя модели.

4.3.    Результат проведения эксперимента

Расчет по алгоритму 1 осуществлялся со следующими параметрами (табл. 3):

Т а б л и ц а 3

Исходные параметры расчетов

№	Параметр	Значение
1	layers	201
2	sigma	[1, 2, 3]
3	scale	[1, 1.5, 2]
4	decrease level _	0.95
5	datasets	imdbstfd

После выполнения итерационного алгоритма сжатия слоев было получено девять моделей с различным уровнем удаления весов и числом обработанных слоев. Значения метрик моделей представлены в табл. 4.

Т а б л и ц а 4

Значение метрик моделей после сжатия

Урезание	Метрики	Значение метрик (scale = 1)	Значение метрик (scale = 1.5	Значение метрик ) (scale = 2)	Эталонные метрики
sigma = 1	Accuracy	0.825	0.900	0.875	0.825
	ROC AUG score _ _	0.890	0.892	0.907	0.936
	Fl	0.799	0.882	0.838	0.787
	Precision	0.777	0.882	0.928	0.812
	Recall	0.823	0.882	0.764	0.764
sigma = 2	Accuracy	0.850	0.825	0.825	0.825
	ROC AUG score _ _	0.913	0.902	0.892	0.936
	Fl	0.823	0.799	0.787	0.787
	Precision	0.823	0.777	0.812	0.812
	Recall	0.823	0.823	0.764	0.764
sigma = 3	Accuracy	0.825	0.900	0.825	0.825
	ROC AUG score _ _	0.895	0.930	0.907	0.936
	Fl	0.799	0.894	0.799	0.787
	Precision	0.777	0.809	0.777	0.812
	Recall	0.823	1.000	0.823	0.764

Для всех моделей выполнено условие, при котором значения метрик «обрезанных» моделей должны быть не менее 95% от эталонных. В некоторвк случаях удаление весов даже несколвко улучшило метрики ([ sigma = 1, scale = 1.5], [sigma = 2, scale = 1], [sigma = 3, scale = 1.5]).

Урезанные модели были проанализированы по ряду параметров:

• -    число урезанных слоев;

• -    процент удаленных весов модели;

• -    средний процент удаленных весов в слое.

Результаты анализа представлены в табл. 5.

Т а б л и ц а 5

Анализ параметров сжатия модели

Интервал урезания	Коэффициент масштабирова ния	Число урезанных слоев модели	Процент удаленных весов модели	Среднее значение удаленных весов в слое
sigma = 1	scale = 1	77	0.1157	0.7512
	scale = 1.5	100	0.1848	0.7539
	scale = 2	74	0.0985	0.7555
sigma = 2	scale = 1	84	0.0776	0.9573
	scale = 1.5	78	0.0725	0.9557
	scale = 2	64	0.0776	0.9563
sigma = 3	scale = 1	69	0.1078	0.9900
	scale = 1.5	88	0.1133	0.9904
	scale = 2	84	0.1133	0.9910

В ходе исследования было выявлено, что доля урезанных слоев может достигать половины от общего количества. Причем 88 слоев возможно урезать до 99% без потери качества (sigma = 3, scale = 1.5), но с меньшим общим процентом сжатием модели (0.1133). Слои с такой степенью сжатия можно полностью удалить, так как их вклад носит минимальный характер.

Также из табл. 5 следует, что наибольшее число урезанных слоев (100) и процент удаленных весов (0.1848) принадлежит модели с параметрами сжатия sigma = 1, scale = 1.5. Средний процент урезанных весов в эти слоях составил около 75 процентов параметров. Из чего можно заключить, что неполное удаление параметров по элементам модели приводит к ее большему сжатию.

При значении 1.5 применение коэффициента масштабирования (scale) позволяет повысить качество сжатия, особенно это заметно при удалении весов более 99% в сравнении с урезанием без его использования.

Помимо анализа сжатия, также рассмотрен вопрос степени влияния параметров при урезании на обработанные слои модели (табл. 6).

Т а б л и ц а б

Анализ обработанных слоев в зависимости от параметров сжатия

Интервал урезания	Коэффициент масштабирования	Число урезанных слоев модели	Совпадающие слои в моделях	Разные слои в моделях
sigma = 1	scale = 1	77	35	42
	scale = 1.5	100		65
	scale = 2	74		39
sigma = 2	scale = 1	84	40	44
	scale = 1.5	78		38
	scale = 2	64		24
sigma = 3	scale = 1	69	35	34
	scale = 1.5	88		53
	scale = 2	84		49
scale = 1	sigma = 1	77	36	41
	sigma = 2	84		48
	sigma = 3	69		33
scale = 1.5	sigma = 1	100	51	49
	sigma = 2	78		27
	sigma = 3	88		37
scale = 2	sigma = 1	74	28	56
	sigma = 2	64		36
	sigma = 3	84		56

В относительных единицах соотношение совпадающих слоев при значении интервала sigma, равном 1, 2, 3, в среднем сходится к следующим числам: 0.41, 0.53, 0.43. Аналогично для параметра scale (1, 1.5, 2) получены значения: 0.47, 0.57, 0.36. Из чего сделано заключение, что около половины обработанных слоев отличаются в зависимости от исходного набора параметров, причем это не зависит от того, какой из них брать в качестве базового (табл. 6). Если рассмотреть случай для sigma = 1, то только 36 обработанных слоев совпадают при меняющемся параметре scale, остальные отличаются в зависимости от сжатия модели (42, 69, 39).

Вариация обработанных слоев в зависимости от параметров в половине случаев говорит о том, что каждый раз путь сжатия меняется. Результат вторичного запуска алгоритма представлен в табл. 7.

Повторное применение алгоритма позволило либо незначительно повысить количество удаленных весов, либо никак не изменить исходное значение, что указывает на фильтрацию одних и тех же слоев модели для каждого набора исходных параметров.

В то же время для случая sigma = 3 значительно вырос процент удаленных весов с

0.1133 до 0.1919. В данном случае были урезаны новые слои с относительным удалением 98%, что привело к улучшению сжатия на 70%.

Т а б л и ц а 7

Результат повторного сжатия урезанной модели

Процент урезания	Коэффициент масштабирования	Процент удаленных весов модели	Количество обработанных слоев
sigma = 1	scale = 1.5	0.1887	42
	scale = 2	0.1849	39
sigma = 2	scale = 1.5	0.1849	27
	scale = 2	0.2055	31
sigma = 3	scale = 1.5	0.1919	38
	scale = 2	0.1849	24

5.    Заключение

В ходе проведенного исследования были получены следующие результаты:

• -    разработан метод сжатия слоев на основе фильтрации, который основывается на распределении весов, связанном со структурными особенностями модели;

• -    представлен итерационный алгоритм урезания слоев, позволяющий получить модели машинного обучения с различной степенью сжатия и сохранения заданных метрик на уровне 0.95 от эталонных;

• -    наибольшие значения урезанных весов получены при исходных данных sigma = 1, scale = 1.5 модели и достигало 18,5% от общего числа параметров при среднем сжатии слоя на 75%;

• -    установлено, что число совпадающих и отличающихся урезанных слоев в среднем стремится к 0.5, что указывает на значительное влияние при выборе исходных данных.

В совокупности данные результаты позволили достичь урезания слоев модели при котором качество классификации сохраняется на уровне не менее 0.95 от значения эталонных метрик.