Метод сжатия речевых данных без пауз на основе оптимального квантования по уровню коэффициентов разложения отрезков речевых сигналов по собственным векторам субполосных матриц

Проблема уменьшения объемов битовых представлений речевых данных при их хранении и передаче рассматривается в работах многих авторов, особенно специалистов в области телекоммуникаций, что подтверждается результатами анализа научно-технической литературы [1-4].

При этом отмечаются два основных аспекта: необходимость обнаружения с последующим их кодированием пауз, возникающих между отдельными словами и в режиме диалога занимающих до 60% длительности исходных звукозаписей, и сокращение объемов битовых представлений собственно звуков речи без пауз. Существующие методы сжатия звуков речи без пауз с использованием грубого квантования по уровню основываются на психоакустической модели, что приводит к необходимости применения так называемых субполосных преобразований отрезков (векто- ров) отсчетов речевых сигналов, позволяющих получить другие векторы, подвекторы которых отражают частотные свойства исходного вектора в выбранных диапазонах оси частот. Именно компоненты этих подвекторов подвергаются квантованию по уровню с различными шагами, чем достигается учет частотно-избирательных свойств человеческого слуха. В настоящее время для субполосного преобразования принято использовать процедуру прореживания выходных последовательностей КИХ-фильтров (фильтров с конечной импульсной характеристикой), настроенных на соответствующие участки оси частот. Такая процедура субполосного преобразования не является оптимальной в смысле минимума погрешностей аппроксимации спектров исходных векторов в выбранных частотных диапазонах, что приводит к увеличению погрешностей восстановления данных по квантованным значениям и, как следствие, к ухудшению качества воспроизводимой речи.

В связи с этим авторами предлагается метод сжатия речевых данных без пауз, созданный с применением разработанного математического аппарата на основе собственных векторов субполосных матриц, позволяющего адекватно сформулировать вариационные условия и решить оптимизационные задачи обработки речевых данных.

Математические основы метода

Осуществляется обработка отдельных отрезков (векторов отсчетов) сигнала речи:

х = (%,,. ..,x_Ny              (1)

в соответствии с выбранным равномерным разбиением полосы нормированных частот О < го <  тс на R интервалов V вида

VTT -VrX=Tc/R; VrM = Vr2;

r = l;2... Л-1

одинаковой ширины. В основе сжатия данных используется свойство концентрации энергии речевых сигналов в малой доле частотной полосы, что позволяет использовать аппроксимацию где

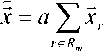
xr = Ar x,

коэффициент Cl при сумме выбирается из усло- вия II A ||2 = m||x|| , что дает a =

где R_m – множество частотных интервалов минимальной суммарной ширины, для которых выполняются условия

^^.(x) = m||x||2;           (6)

0,85 <  m < 0,98;             (7)

где m – множество информационных частотных интервалов, а A_r – субполосная матрица, определяемая элементами:

A,, “ik

I a' k }, i,k = 1,...,N;

sin^ _r (z - A')) - sin^ ,. (z - A:)) Tc^i — A')

i * к -

Z=1

где ^i – собственные числа собственных векторов Qi субполосной матрицы, принимающие значения 0 < Л' < 1 . Подстановка (8) в (3) дает разложение по набору собственных векторов:

(9) reR„, i=\ где pir=aXiail.A = \,..,Jr.         (10)

Так как наборы собственных векторов Qi предполагаются известными, то для восстановления исходного отрезка достаточно сохранять информацию о соответствующих коэффициентах разложения. Проведенные исследования показали, что мощность множества частотных интервалов (int7?J почти для всех звуков русской речи удовлетворяет соотношению int7?m «0,37?.             (11)

Поэтому с учетом равенства J^N/R получаем коэффициент сжатия за счет использования аппроксимации (3) (по количеству сохраняемых чисел):

CH = N /(int R,„ J)«3.      (12)

Следующий шаг заключается в применении к коэффициентам разложения квантования по уровню с малым их количеством. В общем виде процедура квантования описывается следующим образом, если выполняется условие:

A, e O,,, =[^„_1,^„),         (13)

то положить

/3>d_m,m^l,...,K,         (14)

где К – количество используемых уровней квантования.

Проблема заключается в оптимальном выборе границ отрезков в (13) и значений d в (14) в смысле минимизации погрешностей аппроксимации исходных данных квантованными значениями:

^-t ypP,-dj\C = V.,JV^Rm, (15) m=\ Pir=Sm где S„, – множество значений P, ’ удовлетворяющих условию (13). В результате проведенных исследований было показано, что при заданных отрезках o в (13) минимум правой части (15) достигается на множестве уровней квантования, равных соответствующим средним значениям:

d_m = ^P_rI^S_m\m = \-2...K   (16)

P„=s„, где int Sm – мощность множества s m (число попадающих в них значений Pir )•

Введем положительную неубывающую последовательность:

0kk+v,k = V,2... NK-1,    (17)

NK = J-mt R_m,          (18)

причем

Zk ^^Pir\P7d=VP- J; ГеКт

_ Ifllw - P (19) у = тах|Д..|, Vz и reR_m.

Показано, что выполнение условий t,I..=NK,(21)

где(22)

l. -УЛА =o,

(=1

а также выбор уровней квантования в виде

= 1;2... К(23)

дает минимум погрешности аппроксимации ^ к квантованными значениями

-*k=d(24)

когда выполняется условие

ZL,„_A - Zk - ZL,„_1+1,„

Реально вместо операции (24) следует использовать кодирование codzk = log2 m,

имея в виду, что номера уровней квантования целесообразно обозначать двоичными числами разрядности р , так что

K = l^p.                 (27)

Таким образом, количество уровней квантования целесообразно выбирать из множества (2; 4; 8 …). В соответствии с этим в процессе проведения исследований был разработан алгоритм решения задачи (20), (21) с последовательным делением подпоследовательностей на две части, каждая из которых удовлетворяет этим условиям со своими параметрами L, ^{И d}m (так как деление на две последовательности любой длины несложно реализуется последовательным перебором).

Использование стандартизованных последовательностей вида (17)-(19) позволяет не хранить значения уровней (23), а для восстановления данных использовать уровни из заранее сформированной кодовой книги, удовлетворяющей условию

^1т-^т-а¹^=т^П_м    (28)

где

^^l 1^1 >" *" ? ^ К ^ ⁷ ^1 ^ ^2 ^ • • • ^ ^ ^ ■     (29)

Такие кодовые книги сформированы при К = 2; 4; 8 с учетом всех звуков русской речи с усреднением по множеству дикторов.

Для иллюстрации работоспособности и эффективности разработанных метода и алгоритма были проведены экспериментальные исследования, которые показали, что разборчивость речи сохраняется уже при K = 2. Таким образом, с учетом необходимости сохранения знакового разряда и значения Y достигаемый максимальный коэффициент сжатия может быть равен

CH^=nNkN + \l),     (30)

(в предположении 8-разрядности исходных отсчетов). То есть если N достаточно велико, то

CH

= 12.

Выводы

В результате проведенных исследований было установлено, что предлагаемый метод сжатия речевых данных без пауз на основе оптимального квантования по уровню коэффициентов разложения отрезков речевых сигналов по собственным векторам субполосных матриц из m -информационных частотных интервалов с применением кодовых книг квазиоптимальных квантователей позволяет в зависимости от величины разрядности исходных отсчетов указанных сигналов обеспечить коэффициент сжатия до 12 раз.

Необходимо также отметить, что с учетом сжатия пауз в речи, которые могут составлять более 60% от продолжительности диалога, общий коэффициент сжатия как за счет обнаружения и кодирования пауз, так и за счет квантования по уровню коэффициентов разложения отрезков речевых сигналов по собственным векторам субпо- лосных матриц из m-информационных частотных интервалов может достичь величин 20- 25 раз.

Исследования частично финансировались в рамках гранта РФФИ №15-07-01463.