Метод улучшения коэффициента мощности в однофазной сети

В сети переменного тока почти всегда существует сдвиг фаз между напряжением и током, так как к ней подключены индуктивности-трансформаторы, дроссели и главным образом асинхронные двигатели и емкости-кабели, синхронные компенсаторы и др. [1,2]. По цепи, обозначенной тонкой линией на рис. 1, проходит результирующий ток I со сдвигом фаз φ относительно напряжения (рис.2). Ток I состоит из активной составляющей IA и реактивной (намагничивающей) IL. Между составляющими IA и IL сдвиг по фазе 90°. Кривые напряжения на зажимах источника U, активной составляющей IA и тока намагничивания IL показаны на рис.3. В те части периода, когда ток I нарастает, увеличивается и магнитная энергия поля катушки. В это время электрическая энергия превращается в магнитную. Когда же ток уменьшается, магнитная энергия поля катушки превращается в электрическую и возвращается в питающую сеть. В активном сопротивлении электрическая энергия переходит в тепло или свет, а в двигателе она преобразуется в механическую энергию. Значит, активное сопротивление и двигатель преобразуют электрическую энергию в тепловую и соответственно механическую, а катушка (индуктивность) или конденсатор (емкость) не потребляет электрической энергии, так как она в момент свертывания магнитного и электрического полей возвращается целиком в питающую сеть.

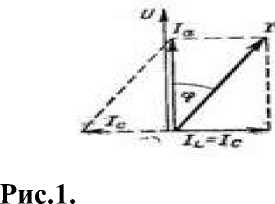
Ток I со сдвигом фаз φ относительно напряжения (рис.2)

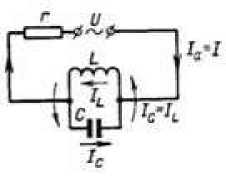
Рис. 2.

Схема электрической цепи

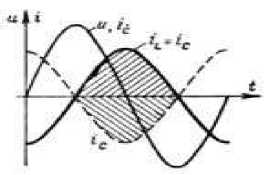
Рис.3.

Кривые напряжения на зажимах источника U, активной составляющей I A и тока намагничивания I L

Чем больше индуктивность катушки (см. рис. 1), тем больше ток I L и сдвиг по фазе (рис. 2). При большем фазовом сдвиге меньше коэфφциент мощности cosφ и активная (полезная) мощность ( P=U∙I ∙cosφ=S∙cosφ ).

При одинаковой полной мощности ( S=U∙I ВА ), которую, например, генератор отдает в сеть, активная мощность P будет меньше при большем угле φ, т. е. при меньшем коэфφциенте мощности cosφ .

Сечение проводов обмотки должно быть рассчитано на результирующий ток I . Поэтому стремление электротехников (энергетиков) заключается в уменьшении фазового сдвига, проводящего к уменьшению результирующего тока I .

Простым способом уменьшения фазового сдвига, т. е. увеличения коэфφциента мощности, является параллельное присоединение конденсатора к индуктивному сопротивлению (рис. 1 цепь, обведенная жирной линией). Направление емкостного тока I C обратно направлению тока намагничивания катушки I L . При определенном выборе емкости C ток I C =I L , т. е. в цепи будет резонанс, цепь будет вести себя так, как будто нет ни емкостного, ни индуктивного сопротивления, т. е. как будто в цепи только активное сопротивление. В этом случае полная мощность равна активной мощности P:

S=P; U∙I=U∙IA, откуда вытекает, что I=IA, a cosφ=1.

При равенстве токов I L =I C , т. е. равенстве сопротивлений X L =X C =ω∙L=1⁄(ω∙C) , будет cosφ=1 , а фазовый сдвиг будет компенсирован.

На диаграмме на рис. 2 показано, как прибавлением тока IC к результирующему току I уничтожается сдвиг. Глядя на замкнутую цепь L и C, можно сказать, что катушка соединена последовательно с конденсатором, а токи IC и IL текут друг за другом. Конденсатор, который попеременно заряжается и разряжается, обеспечивает в катушке ток намагничивания IM=IL=IC, который не потребляется из сети. Конденсатор является своего рода аккумулятором переменного тока намагничивания катушки и заменяет сеть, чем и уменьшается или устраняется сдвиг фаз.

На диаграмме на рис. 3 заштрихованные за полпериода площади изображают энергию магнитного поля, переходящую в энергию электрического поля и обратно.

При параллельном соединении конденсатора с питающей сетью или двигателем результирующий ток I уменьшается до величины активной составляющей I A (см. рис. 2). При последовательном соединении конденсатора с катушкой и источником питания также можно добиться компенсации фазового сдвига. Последовательное соединение для компенсации cosφ не применяется, так как оно требует большего числа конденсаторов, чем при параллельном соединении.

Для компенсации реактивной мощности устройства замерим U, I и подводимую мощность P. По ним определим коэфφциент мощности устройства: cosφ 1 =P/S=P/(U∙I), который нужно улучшить до cosφ 2 >cosφ 1 .

Соответствующие реактивные мощности по треугольникам мощностей будут Q 1 =P∙tanφ 1 и Q 2 =P∙tanφ 2 .

Конденсатор должен возместить разность реактивных мощностей Q=Q 1 -Q 2 =P∙(tanφ 1 -tanφ 2 ).

Подробно рассмотрим пример. Однофазный асинхронный двигатель полезной мощностью P 2 =2 кВт работает при напряжении U=220 В и частоте 50 Гц. К. п. д. двигателя 80% и cosφ=0,6 . Какую батарею конденсаторов надо подключить к двигателю, чтобы получить cosφ 1 =0,95? Подводимая мощность двигателя P 1 =P 2 /η=2000/0,8=2500 Вт. Результирующий ток, потребляемый двигателем при cosφ=0.6, подсчитаем, исходя из полной мощности:

S=U∙I=P 1 /cosφ;

I=P 1 /(U∙cosφ)=2500/(220∙0,6)=18,9 А.

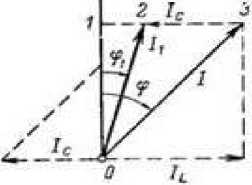
Рис.4. Диаграмма где полный ток I после подсоединения конденсатора.

Необходимый емкостный ток I1 определим на базе схемы на рис. 1 и диаграммы на рис. 2. Схема на рис. 1 представляет собой индуктивное сопротивление обмотки двигателя с параллельно подсоединенной к ней емкостью. От диаграммы на рис. 2 перейдем к диаграмме на рис. 4, где полный ток I после подсоединения конденсатора будет иметь меньший сдвиг φ1 и значение, уменьшенное до I1. Результирующий ток I1 при улучшенным cosφ1 будет: I1=P1/(U∙cosφ1)=2500/(220∙0,95)=11,96 А.

На диаграмме (рис. 4) отрезок 1–3 представляет собой величину реактивного тока I L до компенсации; он перпендикулярен вектору напряжения U. Отрезок 0–1 представляет собой активный ток двигателя.

Сдвиг по фазе уменьшится до величины φ 1 если ток намагничивания I L уменьшится до значения отрезка 1–2. Это получится при включении на зажимы двигателя конденсатора, направление тока которого I C противоположно току I L , а по величине он равен отрезку 3–2.

Величина его I C =I∙sinφ-I 1 ∙sinφ 1 .

По таблице тригонометрических функций найдем значения синусов, соответствующие cosφ=0,6 и cosφ 1 =0,95:

I C =18,9∙0,8-11,96∙0,31=15,12-3,7=11,42 А.

Исходя из величины IC, определим емкость батареи конденсаторов:

I C =U/(1⁄(ω∙C))=U∙ω∙C;   C=I C /(U∙2∙π∙f)=11,42/(220∙π∙100)=(11420∙10^(-

6))/69,08≈165 мкФ.

После подключения к двигателю батареи конденсаторов общей емкостью 165 мкФ, коэфφциент мощности улучшится до cosφ 1 =0,95 . В этом случае двигатель еще потребляет ток на магничвание I m =I 1 sinφ 1 =3,7А. в этом случае активный ток двигателя в обоих случаях одинаков равна: I A =I∙cosφ=I 1 cosφ 1 =11,35А.