Метод улучшения управления первого порядка для дискретно-непрерывных систем

В теории оптимального управления описан целый класс управляемых процессов, для которого характерна с течением времени смена описаний в терминах управляемых дифференциальных систем. Подходы к построению их математических моделей и исследованию, а также используемая терминология, весьма разнообразны и широко представлены в литературе: системы переменной структуры [1] , дискретно-непрерывные системы [2] , логико-динамические системы [3, 4] , импульсные системы [5] , гибридные системы [6, 7] . Одна из возможных схем исследования задач оптимального управления для таких систем состоит в обобщении для них достаточных условий оптимальности Кротова [8 , 9] . Так, в [2 , 10 –12] предложена математическая модель дискретно-непрерывной системы (ДНС). Это двухуровневая модель, в которой нижний уровень представляет собой описания однородных непрерывных процессов на отдельных этапах, а верхний уровень (дискретный) связывает эти описания в единый процесс и управляет функционированием всей системы в целом с целью обеспечения минимума функционала.

Для такой модели получены достаточные условия оптимальности типа Кротова и построены методы улучшения управления [12] . Один из таких методов предложен в [13] . Это метод второго порядка, сложность которого состоит в необходимости решения на каждой итерации для

сопряженных переменных системы векторно-матричных уравнений типа Риккати. Как известно, такая система может и не иметь решения, что требует дополнений алгоритма. Заметим, что к достоинствам метода следует отнести следующий факт: на последней итерации получается решение в форме приближенно-оптимального линейного синтеза управления.

Однако, если положить в сопряженной системе матрицы равными нулю, то получается метод улучшения первого порядка, также дающий решение в форме приближенно-оптимального линейного синтеза управления и не связанный с необходимостью решения матричных уравнений Риккати. Этот метод принципиально отличается от градиентного для ДНС [14] и до сих пор не рассматривался.

Цель работы: ликвидировать указанный пробел и провести сравнение предложенного метода с градиентным на иллюстративном примере.

• 1.    Модель дискретно-непрерывной системы

Пусть задана абстрактная дискретная управляемая система [9] :

• (1)     x(k + 1) = f (k, x(k), u(k)),      k E K = { k i , k i + 1,...,k F } ,

где k — номер шага (этапа), не обязательно физическое время, x и u — соответственно переменные состояния и управления, f — оператор. Все указанные объекты — произвольной природы (возможно, различной) для различных k, U (k,x) — заданное при каждом k и x множество, k I , k F — начальный и конечный шаги соответственно. На некотором подмножестве K ‘ С K , k F / K ‘ действует непрерывная система нижнего уровня

c

• (2)    x c =      = f c (z,t,x c ,u c ) ,          t E T (z) = [t i (z),t F (z)],

  dt

  z = (k, x, ud) ,

  
  

x c E Xc (z,t) С R ^{n ( k )} , uc E U c (z, t, x c ) С R ^{p ( k )} ,

Здесь U c (z, t, x c) — заданное множество.

Оператор правой части (1) имеет вид f (k, x, u) = 9 (z, Y c ), где

Y c = (t i , x I , t F , x^C F ) E r c (z), r c (z) = { Y^C : t i = т (z), x I = ^(z), (t F , x c, ) E r F (z) } .

Здесь z = (k, x, ud) — совокупность переменных верхнего уровня, играющих на нижнем уровне роль параметров, u ^d — переменная управления произвольной природы, t i = т (z), x C = ^(z ) — заданные функции z.

Решением этой двухуровневой системы считается называемый дискретно-непрерывным процессом набор m = (x(k), u(k)), где при k ∈ K′ :

u(k) = (ud(k), mc(k)), mc(k) E Dc (z(k)), mc(k) — непрерывный процесс (xc(k, t), uc(k,t)), t E T(z(k)), Dc(z) — множество допустимых процессов mc, удовлетворяющих на каждом дискретном шаге k указанной дифференциальной системе (2) c дополнительными ограничениями при кусочно-непрерывных uc(k,t) и кусочно-гладких xc(k, t).

Совокупность элементов m, удовлетворяющих всем выше перечисленным условиям, обозначим через D и назовем множеством допустимых дискретно-непрерывных процессов.

Для модели (1) , (2) рассматривается задача о поиске минимума на множестве D функционала I = F (x (k F )) при фиксированных k I = 0, k F = K, x (k I ) и дополнительных ограничениях

• (3)                     x(k) E X (k), x c E X c (z,t) ,

• 2.    Достаточные условия улучшения и оптимальности управления

X (k), X c (z, t) — заданные множества.

Заметим, что модель (1) , (2) удобна для представления неоднородных управляемых процессов. Ее нижний уровень представляет собой описания однородных процессов на отдельных этапах, а верхний — связывает эти описания в единый процесс и управляет функционированием всей системы в целом. В различных задачах управления, в частности в задачах оптимизации, оба уровня рассматриваются во взаимодействии. Взаимодействие с каждой подсистемой нижнего уровня осуществляется через границу этой подсистемы и соответствующего непрерывного процесса γ ^c .

Достаточные условия оптимальности для такой модели получаются по аналогии с условиями Кротова для дискретных и непрерывных систем следующим образом. Из ограничений множеств D и D ^c исключаются дискретная цепочка и дифференциальная система и вводятся функционалы ф (k,x) и ф ^с (z,t,x^c). Последний можно рассматривать как параметрическое семейство функций от аргументов t, x ^c с параметром z , которые считаются непрерывными, и по крайней мере, непрерывно-дифференцируемыми по этим аргументам, где z =

(k, x (k), u d (k) . Кроме того, рассматривается обобщенный лагранжиан по аналогии с лагранжианами Кротова для дискретных и непрерывных cистем:

L

G (x) R ( k, x, u ) G c (z,Y c )

R c (z, t, x c , u c )

M c (z,t) l c (z)

= G (x (k F )) —    ^^  R(k, x(k), u(k))

K \ K ‘ \k F

+ £(G c (z(k),Y c (z(k)))

K ^′

• —    j R ^c (z(k), t, x ^c (k, t), u ^c (k, t))dt^ , T ( z ( k ))

= F (x) + ф (k F , x) — ф (k i ,x (k i )) ,

= ф ^{(k +} 1, f ^(k, ^x, ^{u)) —} ф ^(k , ^x) ,

= ^— ф ^{(k +} 1, У ⁽z, Y ^{c )) +} ф ^(k , ^x)

+ ф ^с (z, t p ,x ^cf ) — ф ^с (z, t i ,x c ),

= ф Х с f c (z, t, x c , u c ) + ф ^с (z, t, xc) .

= sup { R c (z, t, x c , u c ) : x c E X c (z, t), u c E U c (z, t, x c ) } ,

= inf { G c (z, Y c ) : Y c E r (z), x c E X c (z, t F ) } ,

M (k)

l

_ J sup { R (k, x, u) : x E X (k), u E U (k, x) } , = [ — inf { l c (z) : x E X (k) , u d E U d (k, x) } , = inf { G (x) : x E Г П X (K ) } .

t E K \ K ' , k E K ‘ ,

Здесь ф Х с — градиент ф ^с в пространстве (x c ), T — знак транспонирования.

Справедливы следующие утверждения.

Теорема 1. Для любого элемента m E D и любых ф,ф^с имеет место оценка

I (m) — inf I <  Д = I (m) — l.

Пусть имеются два процесса m ¹ E D и m¹¹ E E и функционалы ф и ф ^с , такие что L (m ¹¹) <  L (m¹) = I (m¹) , и m ¹¹ E D .

Тогда I (m ¹¹ ) <  I (m ¹ ) .

Теорема 2. Пусть имеются последовательность дискретнонепрерывных процессов { m s } C D и функционалы ф, ф^с , такие что:

• (1 )    M c (z,t) — кусочно-непрерывна при каждом z ;

• (2)    R (k, x s (k) , u s (k)) ^ m (k) , k E K ;

  
  

  L. ) (R c (z s

  
  

  ^{,t,x c (t) ,u} c о

  
  

  - M ^c (z s ,t)) dt ^ 0, k G K ‘ , t G T (z s );

  
  

• (4 )    G c (z s ,Y^ - l c (z s ) ^ 0, к G K ‘ ;

• (5 )    G (x s (t F )) ^ l.

• 3.    Метод улучшения первого порядка

Тогда последовательность { m s } — минимизирующая для I на D .

Доказательство обоих утверждений дано в [10, 11, 13] .

При построении методов, как правило, отталкиваются от задачи улучшения элемента, которая состоит, по существу, в построении некоторого оператора ш : D ^ D , такого что I(ш(т)) <  I(m) (монотонного по функционалу) [15] .

В [13] построен метод улучшения второго порядка, содержащий в сопряженной системе векторно-матричные уравнения относительно первых и вторых производных функций ф (k, х) , фс (z, t, хс) и дающий решение в форме приближенного линейного синтеза управления на обоих уровнях. Сами функции ф (к, х), фс (z, t, xc) задаются в виде ф = фТ (к) х (к) + 2 ДхТ (к) ст (к) Дх (к) , фс = фсТ (к, t) хс (к, t) + - ДхсТ (к, t) стс (к, t) Дхс (к, t)

+ | Дх ^Т (к) Л (к, t) Дх^с (к, t) + | Дх ^{с Т} (к) Л ^Т (к, t) Дх (к) , где ф и ф ^с — вектор-функции, ст, ст ^с и Л — матрицы, Дх = х — х ¹ , Дх ^с = х ^с — х ^{с 1} . Дополнительная сложность метода состоит в необходимости решения матричных уравнений типа Риккати для матриц σ, σ ^c .

Если в построенном методе положить матрицы ст, ст ^с , Л равными нулю, то получим метод улучшения первого порядка. Основные уравнения метода для этого случая имеют вид:

ф (k F ) т/{^{с ф (к)}

--------------------------I

aF x , ф ^с (k,t F ) = H X c ,

F

И с      с а^с — 1 И"сТ

^H x ^{c + H} x ^c u ^{c H} u ^c u ^{c H} u ^c ,

^{ф (к)}

Hx - HxuHUulHu, к G K\K‘\kF, tF (k)

H x + E^H x I + ^ Т ф ^с (k,t I ) -        H X dt, к G K ‘ .

t I ( k )

При этом

• (8)          Au a (k) = - (H uu ) ^{- 1} (H u + H T u Ax(k)) ,

• (9)        Au a (k, t) = - (H c c u c ) — 1 (H cu c + H c T u c Ax(k) +

+ H cT c u c Ax ^c (k,t)) .

Здесь

H = ( ^ ^T (k + 1) f (k, x(k), u(k)) — 2 (1 — a) | Au (k) | ² , k E K \ K ‘ \ k F [_^ ^T (k + 1) 6 (k, x (k) , x C , x cF )                           k E K ‘ ,

и

• (11)        H ^c = ^ T f ^c (k,x(k),x ^c ,u ^c ) — 2 (1 — a) | Au ^C (k) | ² ,

• 3.1.    Алгоритм метода

Au = u — u I , Au ^c = u ^c — u ^{c I} , a E [0,1] — весовой коэффициент. Предполагается, что x ^c (k, t i ) = ^ (k, x (k)).

Нетрудно видеть, что получающийся при этом метод первого порядка принципиально отличается от градиентного метода. Формулы для приращений управляющих воздействий зависят от приращений состояний верхнего и нижнего уровней. Таким образом, как и в методе второго порядка, решение является приближенно оптимальным линейным синтезом.

Как уже указывалось выше, метод предназначен для решения задачи улучшения, которая состоит, по существу, в построении некоторого оператора ш : D ^ D , такого что I(w(m)) <  I (m) (монотонного по функционалу) [15] . При некотором заданном начальном элементе m 0 такой оператор генерирует улучшающую, в частности, минимизирующую последовательность { m s } : m s +1 = w(m s ).

В целом, получается следующая итерационная процедура.

• 1.    «Слева направо» просчитывается ДНС (1) , (2) при u = u s (k), u ^c = u S (k,t) и заданных начальных условиях, получается соответствующая траектория (x _s (k), x S (k,t)).

• 2.    Задается значение регулятора α .

• 3.    «Справа налево» разрешается ДНС (4) – (7) относительно вектор-функций ψ и ψ ^c .

• 4.    Просчитывается «слева направо» исходная ДНС (1) , (2) при u d = u d (k) + Au, u ^c = u S (k,t) + Au ^c , где Au, Au ^c находятся по формулам (8) , (9) . Вычисляются m s +1 и I (m s +1 ).

• 4.    Пример

Процесс итераций заканчивается, когда | I s +1 — I s | ~ 0 с заданной точностью.

Как и в [13] , имеет место следующее утверждение.

Теорема 3. Пусть для ДНС (1) , (2) построена указанная итерационная процедура и функционал I ограничен снизу. Тогда она генерирует улучшающую последовательность элементов { m _s } ∈ D , сходящуюся по функционалу, т.е. существует число I ^∗ , такое что I * <  I (m s ), I (m s ) ^ I * .

Рассмотрим работу метода на примере системы, динамика которой включает в себя два этапа.

1-ый этап:

x 1 = (xc)2(xc — u)2, x2 = x1x2 + 3u3, x1(0) = — 1, x2(0) = — 1, t G [0, 2].

2-ой этап:

x 1 = (x C — t) 2 + u ² , t G [2, 3].

Функционал имеет вид: I = x 1 (3) ^ min.

Построим ДНС. Нетрудно видеть, что K = 0,1, 2. Поскольку оба этапа связаны через переменную x ₁ , то она и играет роль x , а дискретный процесс верхнего уровня принимает вид:

x(0) = x 1 (0, 0) = — 1, x(1) = x 1 (0, 2), x(2) = x 1 (1, 3),

I = x(2), x i (1,2) = x(1), e = x(1).

Основные конструкции имеют вид:

h ^c (0, t, x 1 ,x 2 ,u, <, ^ 2 ) = <  ((x 1 ) ² (x 2 — u)²) +

+ Ф 2

^ x 1 x 2 + 3 u ³^) — |(1 — a) | Au |² ,

H ^c (1,t,x 1 ,u,^ c ) = <  ((x c — t) ² + u ² ) — |(1 — a) | Au | ² .

Начальное управление: u I = 0.5, I I = 1.98. Результаты и сравнительный анализ представлены на рис. 1 , 2 и таблице 1 .

Как видно из таблицы и графиков, градиентный метод потребовал вдвое больше итераций.

Заметим, что при других начальных управлениях u I = — 1, 0, 1 принципиальных изменений не произошло, результат был получен в обоих методах за то же число итераций.

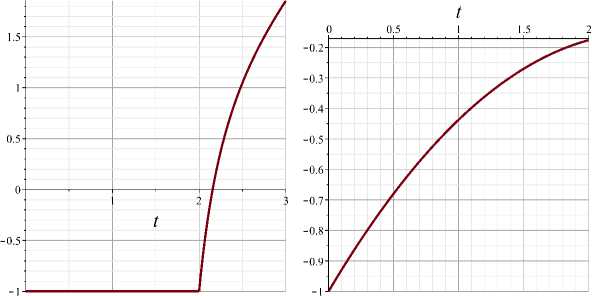
Рис. 1. Переменные состояния: x ^c ₁ (слева) и x ^c ₂ (справа)

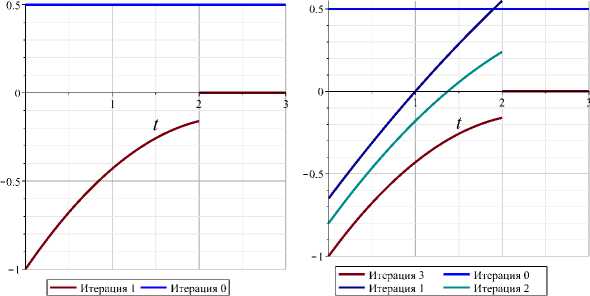
Рис. 2. Графики управлений: метод 1-го порядка (слева), градиентный метод (справа)

Таблица 1. Значения функционала в ходе вычислений

Номер итерации Метод 1-го порядка Градиентный метод

0	1.98	1.98
1	1.85	1.92
2		1.88
3		1.85

Заключение

Таким образом, в работе предложен метод улучшения управления первого порядка для ДНС как модификация более сложного метода второго порядка. Указанный метод принципиально отличается от широко распространенного на практике градиентного метода. На последней итерации метод дает решение в форме приближенно-оптимального линейного синтеза управления. Приведен иллюстративный пример.