Метод управления фазово-частотной характеристикой волоконной брегговской решетки

В настоящее время развитие волоконных лазеров ультракоротких импульсов (УКИ) может привести к замещению ими лазеров, построенных на. объемной оптике, в диапазоне энергий до 100 мкДж и длительностью импульса 100 фс и более [1, 2]. Волоконные лазеры имеют своим значительным преимуществом технологичность, эффективность, устойчивость к внешним воздействиям. Как правило, волоконные лазеры УКИ строятся по chirped-pulse amplification (CPA) схеме, содержащей принципиально четыре элемента: задающий генератор, стретчер, усилитель, компрессор (рис. 1). Стретчер растягивает импульс во временном пространстве за. счет внесения дисперсии групповой задержки ( Group Delay Dispersion) для минимизации нелинейных эффектов в усилителе, а. компрессор работает обратно стретчеру — сжимает импульс.

При этом принципиально, что компрессор выполнен уже не в волоконном формате, а. в объемном. Это может быть и компрессор на дифракционных решетках или же объемная брегговская решетка, и т. п. Для стретчера. же наиболее целесообразно в одномодовом волоконном лазере использовать волоконную брегговскую решетку (ВБР). Таким образом,

«Московский физико-технический институт (государственный университет)», 2018

стретчер и компрессор зачастую представляют собой элементы, работающие на разных принципах. Поэтому идеальное согласование этих двух элементов представляет практическую трудность при построении CPA-лазера. Несогласованность фазово-частотных характеристик стретчера и компрессора значительно ухудшает качество сжатого импульса, приводит к его искажению образованию импульсов-сателлитов [3].

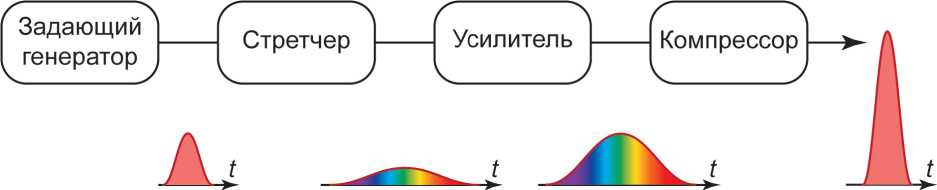
Рис. 1. Схема СРА-лазера

В данной работе рассматривается метод управления фазовой характеристикой ВБР в процессе ее изготовления. Компрессор и его фазовые свойства лежат за пределами рассмотрения данной работы и будем считать, что его фазовая характеристика полностью известна и дана.

2.    Фазовая характеристика ВБР

Отражающая функция волоконной брегговской решетки может быть полностью описана комплексной амплитудой отражения г (ш) = А (ш) е*), где ш — угловая частота электромагнитных колебаний, А (ш) — модуль комплексной амплитуды отражения, 0 6 А (ш) 6 1, ^ (ш) — фаза комплексной амплитуды отражения.

Обе функции действительные. Тогда измеряемый спектр отражения решетки по мощности будет представлять собой функцию А2(ш).

Для брегговских решеток с плоским спектром отражения, у которых А (ш) = const в некотором диапазоне частот, физический смысл функции вносимой фазы ^ (ш) может быть раскрыт через ее производную

^^) = т (ш) как групповая задержка оптического импульса на несущей частоте ш, отраженного от решетки. В случае, когда А (ш) = const, искажение спектра падающего импульса будет искажать также его форму, и поэтому говорить о функции т (ш), как о групповой задержке, можно лишь в некотором приближении. Поэтому в общем случае будем рассматривать функцию ^ (ш) как фазу, вносимую в электромагнитные колебания для волнового пакета при отражении от ВБР.

Для линейно чирпированной решетки зависимость длины волны Брегга от продольной координаты имеет вид Ав_гадд = Cz + Aq. Тогда в случае плоского спектра отражения из геометрических соображений (рис. 2) получаем

• ^{т (ш (А))} = ^ с- 0) ~ ^-(ш - ^ш0) ^с°Т ~ - ^(ш - ^шо) ^2,           ⁽¹⁾

к_Д U д                            Н к_Д CU д                       М \_Д С где соответственно ид — групповая скорость, с — скорость света., п — показатель преломления среды, шо = 2^c/Aq.

Интегрирование (1) дает ы                          2

• * (ш)= Z t (

Ш 0

Учитывая, что в (2) член нулевого порядка — это фаза отраженного импульса, а член первого порядка отвечает за время отражения импульса от решетки, можно вынести эти члены из рассмотрения работы CPA-лазера и без нарушения общности считать их равными нулю. Тогда для линейно чирпированной решетки

У ^(ш) =

-

ш

1 А2п

2 ттСс2

=ш212

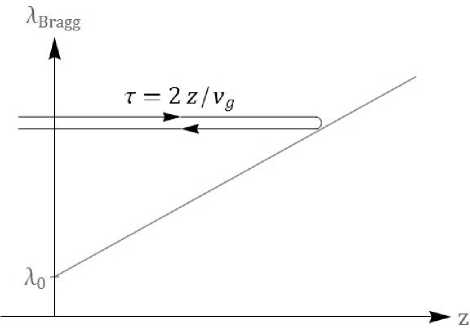
Рис. 2. Геометрическое представление ВБР как распределенного в пространстве зеркала.

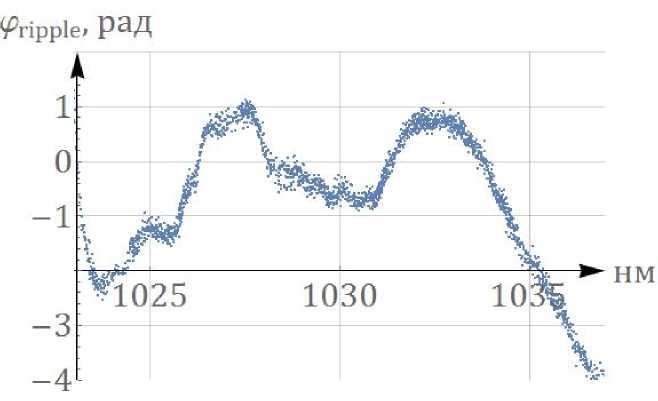
Рис. 3. Пример типичной функции y _rtppi_e

То есть такая решетка, должна, вносить только лишь дисперсию групповых скоростей. Однако несколько факторов приводят к отклонению от идеальной параболической зависимости:

• •    При выводе этой формулы использовалось приближение линейно чирпированной по частоте решетки, что справедливо лишь для решеток с узким спектром.

• •    Отклонения от идеального распределения периода, изменения показателя преломления внутри оптического волокна. Например, при записи решетки методом фазовой маски, ее неточности производства, напрямую переходят в неточности положения штрихов показателя преломления [4].

• •    И главный источник, вносящий случайную ошибку, — искривление волнового фронта, пучка. УФ-лазера, который используется для записи ВБР [5].

3.    Сигма-аподизация

Тогда для реальной ВБР функцию у (ш) удобно записать как

У (ш) = ш212 + Угірріе (ш) , где ргіРРіе (ш) — малая функция, отвечающая за неидеальность характеристики ВБР.

Фазовая характеристика ВБР может быть измерена разивши способами [6-8]. Для любого метода число 32 и функция р_гі_РРі_е однозначно определяют фазовые характеристики решетки. Типичная зависимость р_гі_РРі_е (ш (А)) для ВБР, работающей на 1030 нм, представлена на рис. 3.

Предлагается методика управления фазовой характеристикой в процессе записи ВБР. В основе этого метода лежит зависимость длины волны Брегга Ав_гадд от п_е j j — эффективного показателя преломления для фундаментальной моды световода:

Авгадд (г) = 2Пе// (г)Л(г), где Л — локальный период записанных штрихов брегговской решетки. Экспонирование УФ-излучением повышает средний показатель преломления neff в чирпированной ВБР и тем самым влияет на распределение длин волн Брегга внутри решетки, что в свою очередь переходит в изменение ее фазовой характеристики [9].

Записанную решетку помещают в стенд, где пучок УФ-лазера, отражаясь от зеркала под 45 градусов, падает на оптическое волокно с записанной ВБР, рис. 4 [10]. При этом зеркало находится на линейной моторизированной подвижке с автоматическим управлением. Таким образом, при перемещении зеркала с различной скоростью разные части записанной ВБР дополнительно приобретают разный средний показатель преломления Ап_ст (г), что меняет фазовую характеристику отраженной волны. Назовем этот процесс сигма-аподизация, т.к. в литературе зачастую функция Ti_ejj (г) называется буквой <г(г) [11].

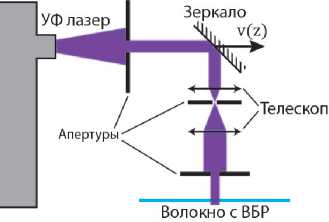
Рис. 4. Экспериментальная схема, неоднородного экспонирования УФ-излучепием

Три апертуры служат для очищения модового состава, пучка, и вырезания из него наиболее когерентной части. А телескоп Кеплера кроме модового фильтра выполняет роль компенсатора, расходимости пучка.

Легко понять, что если наведенный показатель преломления Ат^ (г) пропорционален поглощенной энергии УФ-света, то для непрерывного или квазинепрерывного излучения Ап_ст (г) ~ 1/г (г), г де г (г) — скорость движения зеркала, когда центр пучка падает на координату г решетки. При этом аналогично [12, 13] можно показать из простых геометрических соображений, что изменение показателя преломления Ат^ (г) в первом приближении изменяет фазовую характеристику

Z t( w )

Ар (ш) ∼

Ап_ст (г) Сг.

Следовательно,

А„ , (г) = ^{С А у (}У ^{( г ))}

Сг

С Ар (ш ^ ) Сш ^      С Ар (ш ^ )    2tvcC

Сші    Сг         Сш1   (Сг + А0)2 , где wt (г) = 2ттс/Аі (г) отображает зависимость длины волны Брегга от координаты. Получаем, что траектория движения подвижки должна подчиняться формуле:

г (г) ~

^(Сг + ^Ао) 2 лсС

/ dAy (wt) А ¹

V dwt        ¹

где коэффициент пропорциональности определяется путем соответствующей предварительной калибровки.

В силу предположений о линейности чирпа и плоского спектра отражения решетки, а также в силу того, что для полного рассмотрения требуется учитывать волновой характер отражения от брегговской решетки, а не пользоваться простым геометрическим представлением, формула (3) является лишь приближенной. Поэтому проведение операции сигма-аподизации может изменить фазовую характеристику решетки с некоторым отклонением от формулы. Для получения приемлемого результата на практике необходимо провести сигма-аподизацию от двух до четырех раз.

4.    Экспериментальные результаты

Ниже на рис. 5 представлены измеренные с помощью метода интерферометрии белого света функции y._rippi_e (w) стретчера и компрессора до и после трех итераций сигма-аподизации стретчера.

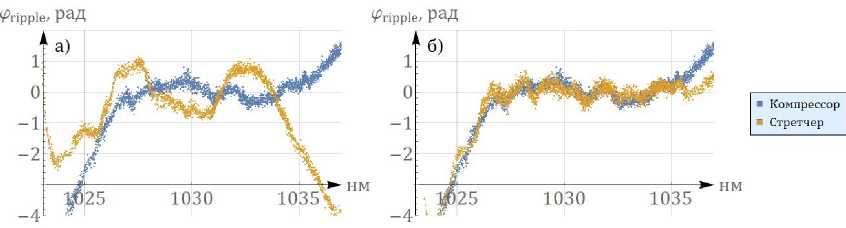
Рис. 5. y _rippie до а) и после б) трех итераций сигма-аподизаций

Как можно заметить, фазовые характеристики становятся близки с хорошей точностью. Это приводит к улучшению качества выходного сжатого оптического импульса из СРА-лазера.

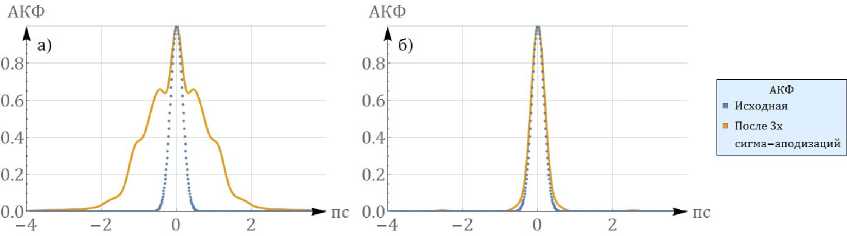
Рис. 6. АКФ сжатого импульса, до и после трех итераций сигма-аподизации. Синие точки — АКФ выходного импульса при y _rt_ppi_e = 0, что должно наблюдаться при идеальном согласовании стретчера. и компрессора.

Зная фазовую характеристику стретчера. и компрессора, можно рассчитать автокорреляционную функцию (АКФ) выходного импульса, из СРА-лазера. Используется приближение, что на. входе в стретчер попадает спектрально-ограниченный импульс со спектром шире, чем спектр отражения стретчера, и в усилителях нет нелинейных эффектов.

На рис. 6 представлена рассчитанная из модели АКФ импульса для стретчера до и после трех сигма аподизаций. Видно, что АКФ сжатого импульса приобретает вид, приближенный к функции Гаусса.

5.    Выводы

Представлен метод управления фазово-частотной характеристикой спектра отражения волоконной брегговской решетки. Показано применение данного метода для приведения в соответствие фазовых характеристик стретчера и компрессора в СРА пикосекундном лазере. Показано теоретически, что данный метод должен приводить к существенному повышению качества сжатого импульса на выходе СРА волоконного лазера.

6.    Благодарности

Работа выполнена при поддержке коллектива отдела научно-исследовательских разработок ООО НТО «ИРЭ-Полюс» (базовая организация кафедры фотоники МФТИ), а также благодаря передовому материальному оснащению исследовательской лаборатории на базовой организации.