Метод волн при математическом моделировании воздействия импульса давления на пьезоэлектрический слой

Уравнения движения линейно-упругого тела в декартовой системе координат ОХхХгХъ Имеет вид [1] д°ч    д2 и

"X^=р Иё где и ( и_х, u ₂, и ₃) напряжений, р -

- вектор смещений, гт - компоненты тензора плотность среды. В рамках линейной теории пьезоэлектричества рассмотрим динамическое деформирование пьезоэлектрического слоя, которое инициирует продольные плоские электроупругие волны с вектором     смещений и (их, u2, и3)        -

U = о, и ₂ = о, u ₃ = u ₃ ( x ₃, t ) ,  напряженностью электрического поля E

E = 0, Е ₂ = 0, E ₃ = E ₃ ( x ₃, t ) и вектором электрической индукции d . Фазовая плоскость волн параллельна свободной границе слоя ( плоскость OX 1 X 2 )

и распространяется вдоль оси X3 - оси симметрии высшего порядка пьезоэлектрика, которая перпендикулярна границе. Волны создаются импульсом давления   P(t), действующим на свободную границу и отражаются от другой границы, условия закрепления которой могут изменяться для различных задач. Условия отсутствия поверхностно распределенного заряда на границах и объемного заряда внутри пьезослоя , -  „                               дD,   „ позволяют свести уравнение    div D = 0 к уравнению      —- = 0 ,

5 х₃

интегрирование которого дает D ₃ = 0 .

Уравнения состояния линейного пьезоэлектрического анизотропного тела для определенного выше вида деформаций имеют вид [2]

^ 11	= c 3 ^ 3 - e 3i E3
^ 22	= c 23 ^ 33 - e 32 E 3
^ 33	= c^ 3 ^ 3 - e33E3
^ 23	c 43 £ 33   e 34 E 3
^ 13	= c 53 £ 33 - e 35 E 3              (2)
_ ^ 12	= c 63 ^ 33 - e 36 E 3

D 1    e 13 ^£ 33 + ^ 13 ^E 3

D3	e 23 ^ 33 + ^ 23 E 3

D ₃ = e_{3 3}^ ₃ + ^₃ E₃

где ^ - компоненты тензора деформаций, e_y - пьезоэлектрические

модули, c_y - упругие постоянные, ^ - диэлектрические проницаемости.

Если выразить компоненты тензора деформаций через подставить (2) в (1) , то получим систему уравнений

перемещения и

	д 2 u3	дE  .
c 53	дx 3 2	— e —3- e 35 - дx3	= 0
c 43	д 2 u3 дx 3 2	дE3 e 34 0x3	= 0
c 33	д 2 u3 д x 32	дE3 - e 33 —3 5 x 3	д 2 u3 = P —Г" д t 2

Для кристаллов Ромбической, Тетрагональной, Тригональной, Гексагональной и Кубической систем ( всего 23 класса симметрии ), и пьезокерамики, поляризованной по оси OX первые два уравнения (3)

выполняются тождественно, а третье, с учетом D ₃ = 0 , приводится к

волновому уравнению [4] :

₂ д ² и₃   д ² и₃

дх ₃²      дt² ’

где c =   ^С 33 ^{+ e} 33 / ^£ 3 3

V P

(4) ,

с последующим вычислением напряженности электрического поля

E (0,0, Е ₃)    по формуле :

_{Е =} _ ^e 33 ^д и 3

s33 дх3

(5)  .

и а ( x 3 ,0) = 0

д и 3 ( x 3 ,0) ₌₀     ⁽⁶⁾ .

Начальные условия для функции u ₃ ( x ₃, t) :   <

I д t

Решение уравнения (4) со смещениями границ пьезослоя – u ₃ (0, t ) = д ( t ); u ₃ ( l , t ) = д ( t ) ( l - толщина слоя ) строится на основании интеграла Даламбера в виде сумм бегущих и отраженных волн [3]:

2 nl x3              2 nl   x3            *  (2 n +1) lx и3 = Za(t-----)-La(t--+—)+ZM2(t -------+—)-Z n=0          c     c     n=1          c     c     n =0               c        c где t* = t -- , а д (t) = 0, при t < 0 ;  ^ (t*) = 0 при t < 0.

c

^ 3 ⁽ t

*

—

(2 n +1) l  x₃

---)

cc

В случае жесткого закрепления границы пьезоэлектрического слоя, на который не действует импульс давления, в полученной формуле необходимо положить р ( t ) = 0 .

Для определенности будем считать что граница x3 = l упруго закреплена с коэффициентом жесткости K :

^зз(l, t) = -K • из(l, t)                (7) , а на другую действует импульс давления

^ зз (0, t ) = P ( t )                    (8) .

Реализация граничных условий (7) , (8) для нормальных напряжений ^ 33 (x , t ) :

2 ^d U

^33(x, t) = Pc ox3

приводит к системе двух дифференциально-разностных уравнений

• (9)    1-го порядка относительно функций р 1 , р ₂ :

^{р (} t ) = ^{2( s} 1 ^- s 2 ) ^- P ⁽ t)/ Pc

Р' (t) = 2(s^ - s,) + 2^' (t) - K • ^ (t) / pc где

s - 2

,   2( n + 1) L            z   2( n + 1) L

= ^ ^ 1 ( t -  ---^); S 1 = ^ ^ 2 ( t - ----4;

n =0              c             n =0              c которая может быть решена численно методом Рунге-Кутта .

Напряженно-деформированное состояние пьезоэлектрика и напряженность электрического поля получается линейной интерполяцией накопленных массивов р- 1 , ^ ₂.

Предложенная методика расчета напряженно-деформированного и электрического состояния пьезоэлектрического слоя может быть использована для любого из 23 классов симметрии пьезоэлектрических кристаллов. Если для какого-либо класса e33 = 0 ,то пьезоэлектрическая связь не проявляется, и соответствующая напряженность электрического поля равна нулю. Эффективность предложенного численного метода связана с тем, что удается свести численное интегрирование волнового уравнения с двумя независимыми переменными (т.е. уравнения с частными производными ) к интегрирования системы обыкновенных дифференциально-разностных уравнений.

На рис. 1 предоставлены результаты расчета разности потенциалов в пьезоэлектрическом слое на основе пьезокерамики титанат-цирконата свинца PZT-4 .

Расчетная толщина всего пьезоэлектрического слоя 10 мм., импульс давления имеет форму полуволны синусоиды с базой 10 мкс. и амплитудой 4 МПа. Жесткость упругого поджатия K равна 8.65 •Ю ⁷ Н / м ³ . Расчет произведен во временном интервале от 0 до 10 мкс.

□ во л ьт               ~ PZT 4

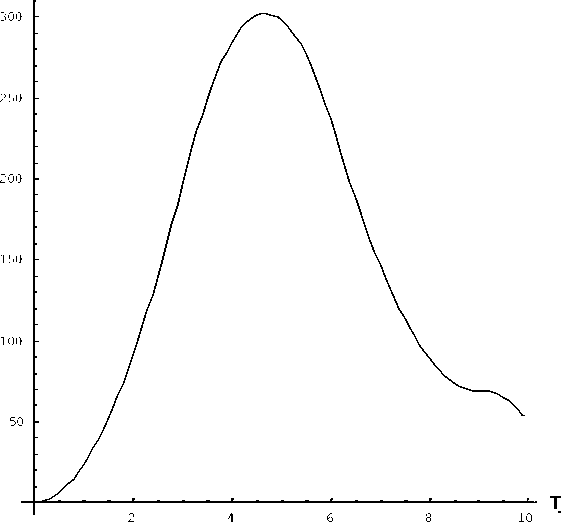
Рис. 1. Электрическое напряжение.