Метод выбора технологии создания параллельного специального программного обеспечения с временной параметризацией

Цитирование: Толмачев А. А. Метод выбора технологии создания параллельного специального программного обеспечения с временной параметризацией / А. А. Толмачев, М. А. Аксенов, Д. С. Викторов, А. А. Филонов, И. В. Лютиков // Журн. Сиб. федер. ун-та. Техника и технологии, 2022, 15(8). С. 1000–1008. DOI: 10.17516/1999-494X-0446

В настоящее время в Вооруженных силах Российской Федерации в целом и в Воздушнокосмических силах в частности проводятся работы по совершенствованию информационно-управляющих систем в целях повышения оперативности и устойчивости управления, данные факторы становятся решающими в современной войне [1]. Одним из важнейших элементов в этой системе является специальное программное обеспечение (СПО), которое дает возможность исследования сценариев различных форм и способов применения средств воздушнокосмического нападения и группировок воздушно-космической обороны в виде имитационного машинного эксперимента в процессе выработки и принятия решения органами военного управления [2].

В результате проведенного анализа было установлено, что масштабируемость специального программного обеспечения моделирующих систем – важный технический аспект, предполагающий расширение их возможностей путем включения новых программных реализаций моделей [3]. Очевидно, что данные модели должны быть адекватны. Подсистема моделирования должна представлять эффективные методы доработки моделей и замены их более совершенными. С усовершенствованием модели растет ее вычислительная сложность. Наличие – 1001 – множества сложных моделей определяет целесообразность распределения имитационных моделей по нескольким вычислителям (ядрам, процессорам).

Для совершенствования специального программного обеспечения потрачено немало временных, финансовых и интеллектуальных ресурсов. Огромный накопленный опыт и уже разработанное специальное программное обеспечение следует сохранять, модернизировать и повышать эффективность, используя технологии параллельного программирования.

В результате анализа технологий параллельного программирования в интересах преобразования унаследованного программного кода [4] определено, что оптимальным вариантом повышения эффективности является модернизация существующего унаследованного кода путем добавления определенных специальных операторов средств распараллеливания. Выбор технологии для распараллеливания уже имеющегося СПО необходимо проводить на основе сравнения по ряду показателей (метрик) эффективности возможных технологий распараллеливания между собой и с последовательной версией СПО. Показателями эффективности для сравнения могут быть [5]: время отклика, время выполнения, пропускная способность, ускорение, производительность, а также выбор их комбинации.

При модернизации унаследованного СПО для распараллеливания, как правило, используется одна технология параллельного программирования. Проведенный анализ [6] показывает, что разные технологии имеют разную эффективность распараллеливания в зависимости от размера распараллеливаемого цикла как элемента кода.

Предполагаем, что для получения максимальной эффективности распараллеливания при модернизации кода необходимо:

• 1.    Выбор технологии распараллеливания выполнять перед каждым запуском цикла в автоматическом режиме с использованием накопленной статистики.

• 2.    Время выбора технологии должно быть значительно меньше времени обработки информации в цикле.

• 3.    Для оптимального выбора технологии необходим поиск функциональной зависимости количества повторений в цикле и типом технологии [7].

Для разрешения данного предположения разработан и предлагается новый метод распараллеливания программы, который базируется на том, что написанный один раз параллельный программный код может быть выполнен разными технологиями параллельного программирования в зависимости от задач и входных параметров. Такими параметрами могут выступать параметры цикла и имеющаяся временная статистика предыдущих запусков. При этом в процессе работы готовой параллельной программы может применяться один из методов распараллеливания:

• 1.    Последовательный запуск технологии параллельного программирования не используется.

• 2.    Выбирается одна технология, при которой общее время выполнения программы будет минимальным.

• 3.    Технология выбирается при каждом запуске цикла, чтобы время выполнения этого цикла было минимальным.

Для третьего метода распараллеливания, когда технология с минимальным временем выполнения выбирается при каждом запуске цикла, можно добиться ускорения расчетов по сравнению со вторым методом. Суммарное время работы программы обозначено как

,

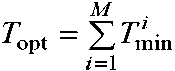
где 1-м - минимальное время работы i- ого цикла среди рассматриваемых технологий параллельного программирования, M – общее число вызовов распараллеленного кода.

Предложен метод, позволяющий вероятностно выбирать технологию распараллеливания для каждого вызова распараллеленного кода и одновременно сократить параметр времени выполнения программы путем оптимизации выбора технологии распараллеливания на этапе выполнения программы. Математически можно представить эту задачу в следующей формулировке

,

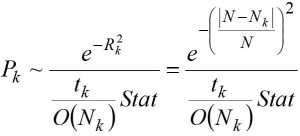
где Pk - вероятность выбора к-ой технологии среди n технологий параллельного программи- рования;          – относительное расстояние между требуемым значением числа итераций цикла в ближайших статистических данных; O(Nk) - сложность алгоритма; N- число итераций цикла; Stat – число (объем) накопленной статистики.

Метод имеет сходство с методом к ближайших соседей тем, что ближайшие данные в статистике оказывают большее влияние по сравнению с остальными. Вероятности выбора номера технологии параллельного программирования зависят от имеющихся статистических данных и от текущих временных параметров вызова распараллеливаемого кода.

Расчет вероятности осуществляется согласно следующим принципам:

• -    при отсутствии статистических данных вероятности выбора разных технологий распараллеливания одинаковы и равны 1/ n , где n – количество имеющихся технологий;

• –    чем больше время работы с указанной технологией, тем меньше вероятность ее выбора (берутся статистические данные для данной технологии с наиболее близким размером цикла), при известной сложности алгоритма O ( N k ) (О - нотации) время будет пересчитываться на единицу сложности;

• -    степень влияния статистических данных разных технологий различна и зависит от «расстояния» от запрашиваемого размера цикла N до размера цикла в статистических данных, ве- _2^2 роятность пропорциональна величине ;

• -    чтобы избежать выбора одного и того же значения номера технологии используется зависимость от числа накопленной статистики для данной технологии: чем меньше статистики, тем больше вероятность выбора этого значения.

Процесс выбора номера технологии распараллеливания является случайным событием, в нашем случае он функционально зависит от ряда случайных параметров.

Задача сводится к нахождению функциональной зависимости номера технологии распараллеливания (Nтр.i) от количества итераций (N), а именно Nгр.i = f (Ni), что является задачей классификации. Если количество технологий параллельного программирования больше двух, то данная задача является задачей многоклассовой классификации. Для повышения качества – 1003 – работы классификатора данные текущего запуска распараллеленного кода сразу же необходимо добавлять в статистику для использования при классификации последующих запусков распараллеленного кода. Значит, необходимо разработать метод выбора технологии создания параллельного специального программного обеспечения с учетом параметра времени обработки информации.

Таким образом, номер технологии распараллеливания будет являться функцией от количества итераций запускаемого цикла, данных статистики и времени выполнения цикла:

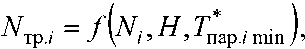
где N_i – количество итераций цикла, H – статистические данные по ранним запускам распараллеливаемого кода, ^nap./ min – минимальное время выполнения цикла. Статистические данные представляют собой тройки «количество итераций цикла» – «номер технологии» – «время работы», в табл. 1 показан пример статистических данных.

При использовании предлагаемого метода возникает необходимость оценки степени адекватности данного выбора, для этого предлагается использовать метод статистического моделирования (статистических испытаний). Суть данного численного метода состоит в получении оценок вероятностных характеристик, совпадающих с решением аналитических задач. Основной идеей метода статистического моделирования является замена детерминированной (при известных параметрах) задачи эквивалентной схемой некоторой стохастической (со случайными элементами) системы, выходные характеристики которой совпадают с результатом решения детерминированной задачи. Конечно, если произвести такую замену, погрешность выбора будет высокая, однако эта проблема решается увеличением количества испытаний.

Используем теорему Байеса [8] для перехода от априорных распределений на неизвестную величину к апостериорным распределениям. В нашем случае имеется полная группа несовместных событий (гипотез – по выбору номера технологии) Е ₁, Е ₂, Е ₃, … , Е_n , если нам неизвестны их вероятности Р ( Е 1 ), Р ( Е 2 ), Р ( Е 3 ), … , Р ( Е n ) до опыта, они равновероятны. В результате опыта появляется некоторое событие А (выбор номера технологии), пусть для этого события

Таблица 1. Статистические данные зависимости количества итераций, номера технологии и времени обработки информации

Table 1. Statistical data on the dependence of the number of iterations, technology number and information processing time

Количество итераций Номер технологии Время, сек Количество итераций Номер технологии Время, сек 60 1 2.105 40 3 0.926 60 2 2.425 40 4 0.526 60 3 1.118 30 1 1.811 60 4 0.408 30 2 1.881 40 1 1.921 30 3 0.781 40 2 1.962 30 4 0.526 известны условные вероятности выбора номеров технологий Р(А/Е1), Р(А/Е2), Р(А/Е3), .„, Р(А/ Е^, в нашем случае это условные вероятности классификационного выбора по (1). Как изменятся вероятности гипотез, если стало известно, что событие А (выбор номера технологии) произошло? Эти искомые вероятности Р(Е1/А), Р(Е2/А), Р(Е3/А), .„, Р(En/А) называются апостериорными (т.е. после опыта) вероятностями. Если событие А произойдет с одним из событий Еi, то формула Байеса преобразится р^е,iavESWlPl = PSWlEk, ^    £р(е,)р(а/е,)

где Р ( A ) = Р(Е i ) Р(А / Е 1 ) + Р ( Е 2 ) Р ( А/Е ₂) + _ + Р(Е п ) Р(А/Е п ).

Поскольку сумма условных вероятностей классификационного выбора номера одной из технологий Р ( А / Е 1 ), Р ( А/Е ₂), Р ( А/Е 3 ), .„, Р(А / Е_п ), согласно (1), не равна единице, то классический розыгрыш одного из п несовместных событий [8] к определению выбора номера технологии применен быть не может. Поэтому предлагается определять номер выбранной технологии при использовании формулы полной вероятности и формулы Байеса [8], а затем произвести статистический розыгрыш для определения номера выбранной технологии.

С этой целью введем интересующие нас события:

А - выбор номера технологии распараллеливания программы и соответствующие гипотезы для примера их четырех технологий:

E 1 – выбор технологии № 1;

• Е₂    – выбор технологии № 2;

• Е 3    – выбор технологии № 3;

• Е₄    – выбор технологии № 4.

При таком подходе гипотезы E_i (z = 1л) образуют полную группу несовместных событий. Тогда полная вероятность выбора номера технологии распараллеливания может быть определена по формуле

Р ( A ) = Р ( Е i ) Р ( А / Е 1 ) + Р ( Е 2 ) Р ( А / Е 2 ) + Р ( Е 3 ) Р ( А / Е 3 ) + Р ( Е 4 ) Р ( А / Е 4 ),       (2)

где условные вероятности выбора номера технологии P ( А/Е ^ ) (/ = 1,4) связаны с вероятностями P 1 ; P ₂; P 3 ; Р ₄ (определяемые (1)) соотношениями:

P ( А / E i ) = P 1 ; P ( А / Е 2 ) = P 2 ; P ( А / Е 3 ) = P 3 ; P ( А / Е 4 ) = P 4 .

Поскольку данный этап реализуется при условии, что выбор номера технологии осуществлен (т.е. событие А произошло), то априорные вероятности гипотез P ( E_i ) (/ = 1,4) изменяются и становятся апостериорными P ( E_i/А ) (/ = 1,4), которые рассчитываются по формулам Байеса

^г./л)=М4^а,(г=1л)

События E_i/А (z = 1Л) образуют полную группу несовместных событий и могут быть использованы для розыгрыша выбора номера технологии распараллеливания D в соответствии с известным правилом [3]

О < D <  Р^Е_Х / А) выбор технологии № 1; Р(Е_Х! A^Х / А) + Р(Е₂ /А) выбор технологии № 2; Р(Е₂ / A^2 / А)+ Р(Е₃ / А) выбор технологии № 3; Р^Е₃ / А)+ Р(Е₄ / A) выбор технологии № 4.

Для наглядности рассмотрим конкретный пример. Если никакой априорной информации о состоянии объекта нет, то

P ( E i )-= P ( E 2> = P ( E з>= P ( E 4 ) = 1/4.

Используя метод Монте-Карло [9], найдем значения вероятностей выбора номеров технологий Р ( А/Е i ), Р ( А/Е 2 ), Р ( А/Е з ), Р ( А / Е 4 ).

P ( А/E i ) = P i = 0,5; P ( А/Е 2 ) = P 2 = 0,6;

P ( А IE 3 ) = P 3 = 0,2; P ( А / Е 4 ) = P 4 = 0,3.

Подставив приведенные значения в формулу (2), получим

P ( А ) = 1/4-0,5 + 1/4-0,6 + 1/4-0,2+ 1/4*0,3= 0,4.

Тогда в соответствии с (3)

-0,5-0,6

Р(Е, / А) = ^---- = 0,3125; Р(р₂ / А) = ^---- = 0,375;

V 1    ’     0,4                V ’0,4

-0,2-0,3

pip / Л) = ^---- = 0,125; Р(Ел / А) = ^---- = 0,1875

V ’    0,4              V 70,4

и правило (4) принимает вид:

0 <  D < 0,3125 выбор технологии № 1; 0,3125 <  D < 0,6875 выбор технологии № 2; 0,6875 <  D < 0,8125 выбор технологии № 3; 0,8125 <  D < 1 выбор технологии № 4.

Предположим, что в конкретном розыгрыше генератор случайных чисел выдал число D = 0,564. В соответствии с (4) в данном розыгрыше выбрана технология № 2. При выдаче D = 0,754 выбрана технология № 3. Если в следующем розыгрыше D = 0,272, то выбрана технология № 1, а в очередном розыгрыше при D = 0,913 выбрана технология № 4. В рассматриваемом случае наибольшие шансы имеет технология № 2.

После реализации предлагаемого метода с накопленной статистикой предыдущих запусков была в качестве примера определена технология № 2 (по max P ( А / E ₂) = P ₂ = 0,6). Далее с применением байесовского подхода было получено апостериорное распределение по оцениваемому параметру (номеру выбираемой технологии распараллеливания по max P ( Е₂/А ) = 0,375 с последующим статистическим розыгрышем данного решения, что подтверждает адекватность предлагаемого метода выбора технологии создания параллельного специального программного обеспечения с временной параметризацией.