Метод вычисления индекса сцинтилляции при наличии анизотропных неоднородностей в возмущенной ионосфере
Автор: Шевченко Вячеслав Анатольевич
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 2 т.13, 2015 года.
Бесплатный доступ
Разработан метод вычисления индекса сцинтилляции S 4 принимаемого сигнала на трассах распространения радиоволн в системах спутниковой связи при наличии анизотропных неоднородностей в возмущенной ионосфере. Метод основан на приведении квадратичной формы в аргументах автокорреляционных функций флуктуаций электронной концентрации и фазы к скалярному значению и учете этого при выполнении преобразований Радона и Фурье. Получены выражения, которые позволяют оценить величину S 4 при высоких значениях спектрального индекса спектральной плотности флуктуаций электронной концентрации, а также во всем диапазоне возможных значений отношения радиуса первой зоны Френеля к внешнему масштабу неоднородностей.
Сцинтилляция, анизотропия, неоднородности, ионосфера, автокорреляционная функция, спектральная плотность
Короткий адрес: https://sciup.org/140191751
IDR: 140191751 | DOI: 10.18469/ikt.2015.13.2.02
Текст научной статьи Метод вычисления индекса сцинтилляции при наличии анизотропных неоднородностей в возмущенной ионосфере
В [5] задача определения S4 решена путем применения алгоритма, предложенного в работе [6], для одномерного фазового экрана, и его адаптации к двумерной автокорреляционной функции флуктуаций фазы [5]. Подобный метод, основанный на алгоритме [6], представлен также в [7]. Более корректным является метод нахождения S4 путем усреднения спектральной плотности интенсивности по возможным значениям ее аргументов [4; 8]. Данная спектральная плотность находится из двумерного преобразования Фурье функции, аргумент которой определяется автокорреляционной функцией флуктуаций фазы и пропорционален интегралу автокорреляционной функции флуктуаций электронной концентрации вдоль линии визирования [2-3].
Задачу вычисления S 4 можно существенно упростить, если решить ее для условий слабого рассеяния волн, а затем использовать эмпирическое исправление полученного результата для множественного рассеяния в отсутствие жесткой фокусировки [9-10]. Для условий слабого рассеяния выражения для расчета S 4, учитывающие анизотропность неоднородностей и геометрию трассы распространения, известны в явном виде [4]. Данные выражения получены с использованием аппроксимации степенного закона, справедливой для спектрального индекса p не выше 5 при условии, что радиус первой зоны Френеля существенно меньше внешнего масштаба неоднородностей. Это условие может не выполняться, когда высота с максимальной ионизацией (высота фазового экрана) существенно больше толщины слоя неоднородностей, но теория фазового экрана еще применима ( ). Кроме того, степенным законом со спектральным индексом в пределах до 5 спектральная плотность описывается тогда, когда сцинтилляция является слабой [11]. Когда сцинтилляция становится умеренной интенсивности, для описания спектральной плотности используют гауссовский закон, который ведет себя как степенной с высоким спектральным индексом [6; 11].
Учитывая вышеизложенное, обобщим выражения для расчета S4 в условиях слабого рассеяния на случай произвольной спектральной плотности флуктуаций электронной концентрации для всего диапазона возможных значений отно- шения радиуса первой зоны Френеля к внешнему масштабу неоднородностей.
Полученные выражения для расчета индекса сцинтилляции конкретизируем для спектральной плотности флуктуаций электронной плотности как гауссовской, так и подчиненной степенному закону, в том числе с большим значением спектрального индекса.
Примем, что волна распространяется от космического аппарата (КА) до земной станции через ионизированную область толщиной Nz с неоднородностями электронной концентрации kN^x^zy Геометрия распространения волны показана на рис. 1.
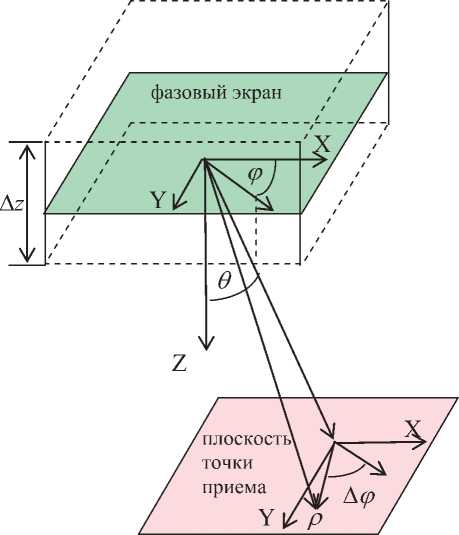
Рис. 1. Геометрия распространения волны
Неоднородности в данной области заменим соответствующим двумерным тонким фазовым экраном, который описывает появление флуктуаций в фазовом фронте волны после прохождения экрана ^ф(х, у) ~ AzZWe (х, у, z) [1]. Точка пересечения трассой распространения волны фазового экрана определяет начало системы координат ( X ; Y ; Z ), ось X которой направлена по географическому меридиану (на север), ось Y – по параллели (на восток), ось Z – строго вниз.
Направление распространения волны длиной X = 2л/к , где k – волновое число, зададим вектором, проекция которого на горизонтальную пло- скость XY имеет единичный вектор (cos ф, sin^y), где ф – азимут. Угол между вектором распространения волны и горизонтальной плоскостью определяется величиной л /2-0, где 0 – угол падения. Фазовый экран лежит в горизонтальной плоскости XY и в точке с координатами (x,y) вызывает случайное изменение фазы во фронте волны М<х,у^, которое описывается стационарным процессом с автокорреляционной функцией В^у) и дисперсией СУ .
Автокорреляционная функция флуктуаций фазы пропорциональна интегралу автокорреляционной функции флуктуаций электронной плотности В№\х,у^ вдоль линии визирования [3]
BM(x,y)=(Xresec0y kz ^B^(x,y,z}lz , (1)
где у, – радиус электрона. Линия визирования с учетом наклонного распространения волны на расстоянии z от фазового экрана проходит через точку с координатами
(х, у, z) = ^р cos N9 - ztg0, p sin ^ф, z)Rz (cp) , (2)
где
p
– радиальная координата,
^ – угол отклонения от азимута Ф в полярной системе координат; RzW> – матрица вращения вокруг оси Z на угол Ф . Для анизотропной среды аргумент автокорреляционной функции (^) в системе координат (S,T,R) имеет величину a , определяемую из следующего выражения [2-3]: = ^^0')°Уь\^^Ф')Е,УьУ, где a – параметр, характеризующий степень удлинения неоднородности вдоль магнитного поля; b – параметр, характеризующий степень удлинения неоднородности поперек магнитного поля; ^ab – матрица, имеющая следующий вид: 0 0 1/6 0 0 1 Неоднородности удлинены вдоль осей S и T. В системе координат (Xp, Yp,Zp), в которой ось Xp направлена на геомагнитный север, ось Yp – на геомагнитный восток, ось Zp – вниз, плоскость XpZp содержит ось S [3]. Угол между этой осью и осью Xp определя- ется углом магнитного наклонения YI ■> угол между осями X и Xp в пло ско сти XY – углом магнитного наклонения V D " Наклонение поперечной оси неоднородностей T примем равным нулю. Переход от системы (X,Y,Z) к системе (Xp,Yp,Zp) выполним путем поворота системы координат на угол V D вокруг оси Z, а затем к системе координат (S, T,R) – путем поворота на угол V i вокруг оси Yp так, что с учетом выражения (2) (s, t, r) = (x, y, z)Rz (- yD )RY (^) = = (p cos A^? - ztg6, p sin ^ф, z^T, где T = Rz^-¥DXAyiY Подставив (5) в (3), получим cr2 = (p cos A^ - ztgO, p sin ^ф, z^RY x (p cos ^ф - ztgO, p sin !\ф, z^ , где Матрица ^y 5 как следует из (8), является симметрической, а ее собственными значениями являются диагональные элементы матрицы ( F^, )" * Выражение (8) после раскрытия его правой части примет следующий вид: 6r2 = /?2^ncos2A^+27'12sinA^9cos A^+r22sin2A^) + + 2/r(r13 cos ^ф + r^ sin ^ф - -(^, cosA^ + rl2sinA^?)lg0j + + z2 (r33 - X^tgG + I\vtg20^= (p, z^F^p, z)T . где F – матрица, элементы которой, как следует из (9), определяются через элементы матрицы ryr cледующим образом: /H =rH cos2 A^? + 2r12 sin A^?cos A^> +/22 sin2^ф; = 'i cos Ac? + sin Ac? - -(rHcosA 12 /22 =?33 -^tg0^rxxtg29. Матрица F имеет собственные значения Я, и ^2 ’ которые являются корнями уравнения det(F-2/) = 0 [12], где I – единичная матрица, и определяются выражениями Матрицу F можно выразить в виде [9] где F = HKKTH"\ Это позволяет представить выражение (7) следующим образом: a2 =(p,z)HKArH-\p,zy = = ^p, z^HK^p, z^HKy. В (16) учтено, что для ортогональной матрицы выполняется равенство H"' =H . С учетом (16) автокорреляционная функция (1) примет следующий вид: R^ФУзЛф^АКsec^)2Z\zx x j/?A Y Q(p, z^HK^p, z^HKy \z. Введем обозначение (fa) = (a-)^- Интеграл в правой части (17) представляет собой преобразование Радона подынтегральной функции ^(a»,(p.f)). где c, = (cos a, sin «У Преобразование Радона данной функции также может быть выражено следующим образом [13]: R^Bx-< (P’ ^)) = J J^c (VGvMpdM)x ^p, Z^cos a, sin «У ) dpdt, где J( ) – дельта-функция Дирака. Сделаем в выражении (19) замену переменных (m,v)=(/7/?,77^)AE, где cos1a sin1a n = д + 2j Xi (21) cos a sin a E = n4^ njh ’ (22) sin a cos a nW dW fsinoA') / x —— Фдд, ^)^. (28) V ok ) Как следует из (28), спектральная плотность ^W должна удовлетворять условию h (°) = 4^ J^2®^Ne Wk = o^, (29) 0 с учетом того, что где СТдд – дисперсия флуктуаций электронной концентрации. С учетом (28) выражение (27) после преобразований примет следующий вид: hW IL ^-'л-1, а якобиан преобразования 8 л" W dp dt J = du du dp dt dv dv . (24) П \4,\A Фдл, \k)dkd Тогда после математических преобразований получим sinoA' ok sincr£ , „ dodk. Второй интеграл является синус-преобразова-нием функции fhhV -й2) . Используя табличный интеграл [15] JY hh (31) где v = 0, a = ph. получим Сделав в выражении (25) замену переменной c^V/^+^/zy, для которой при с> ph к(врРр} справедливо 4л1 ?]^Jhh kp^ Ф^^к-(32) dv do m31 ’ (26) Выражение (17) с учетом (32) примет вид: получим WM) 2 У oBM (er) d^LL Pin V<72-{pldf de. (27) , . (ИлХг^есбХ B^pW- ^ x j^o hp/h ф^ХкУк • В выражении (27) автокорреляционная функция зависит от скалярного аргумента, как при изотропных неоднородностях. Известно, что в этом случае трехмерные автокорреляционная функция вж. M и спектральная плотность ®W связаны следующим образом [14]: Интеграл в правой части (33) с точностью до коэффициента представляет двумерное преобразование Фурье спектральной плотности электронной концентрации, справедливое для изотропного случая [1]. Аргументом автокорреляционной функции флуктуаций фазы является отношение ph . Умножим числитель и знаменатель этого отношения на величину cos 0^2] 22 и учтем, что cos Оур^Ц = cos Ул/det F . (34) Подставив в правую часть выражения (34) значения элементов матрицы F, заданных выражением (10), после математических преобразований получим Индекс сцинтилляции Используя обозначения, принятые в данной работе, выразим спектральную плотность интенсивности I поля волны в точке приема за пределами двумерного экрана следующим образом [2]: cos УЛ/Я1Л2 = ((cos A k^Qx x (cos A^?, sin A^?)r )2, где jg(p,k)exp(zpkr)yp, (41) где Q – матрица, элементы которой определяются следующим выражениями: qu= (гигзз -/'1з)со8У; 912 =921 = Gi2r33 -№¥^e^W» -^bN1^ 922 = (^22^33 — ^23 )cos 9 + 2(rl2r23 — rl3r22 )sin 9 + (36) + (Г11 r22 “ 7 12 )Sin У cos У. Определим геометрический фактор усиления G по аналогии с введенным в работе [3] следующим образом: G 1= т/созУд/Л^ . (37) В случая изотропных неоднородностей значение G = 1 [3-4]. Используя обозначение p = ^pv,pv )= (pcos ^ф, /?sin ^ф\ (38) а также (37), получим вместо выражения (33) следующее: В&ф (p) = к2лХге )2 AzG sec 9 x (Ax)O^ ^dk. k = ^kx,kv\(42) g(p,k) = exp(- /(p = (0,0),k))x x(exp(-/(p,k))-l),(43) /(р,к) = 25д/р)-^(р-У2к)- -5дДр + У2к),(44) где dF – радиус первой зоны Френеля. Обозначим через R1 расстояние между КА и верхней частью области ионизации, через R2 – расстояние между нижней частью области ионизации и земной станцией. Рассматривая только КА на высокой орбите, будем предполагать, что Rx > R2 . В радиолиниях «вниз» и «вверх» с учетом введенных обозначений dF определяется следующим образом [7]: dF X^R2 + ^z3Qc(0)l 2) 2л XH n зесУ _ 5 (45) 2.Л где Hps – высота фазового экрана. Автокорреляционная функция интенсивности определяется как [2] 5/(р)= |ф/(к)ехр(-гркг) Ук, (46) а индекс сцинтилляции находится из выражения [2] где x = Gcosy^/pQp . Выражение (39) аналогично полученному в [3] с учетом того, что интеграл в его правой части с точностью до коэффициента представляет двумерную автокорреляционную функцию флуктуаций электронной концентрации. Для нормированной автокорреляционной функции (39), основываясь на результатах [3], запишем G 1 = ab^det Q . Из сопоставления выражений (37) и (40) следует, что величина 77 cos 9^ЛхЛ2 не зависит от величины ^Ф . S; =В, (0,0)= |Ф2(к)Ук.(47) В радиолинии «вверх» (47) сводится к известному [2] выражению А;=1-ехр(-2^).(48) Определим выражение для S4 для линии «вниз». Известно эмпирическое уточнение результата слабого рассеяния, чтобы приблизительно объяснить множественное рассеяние в отсутствие жесткой фокусировки [9]: A42=l-exp(-A4;J. (49) где ^w – индекс сцинтилляции в условиях слабого рассеяния, когда G/\ф ^ 1 . Для этих условий справедливо приближение exp(/)«1 + / , так что выражение (44) можно аппроксимировать следующим образом: (k cos т, к sin r)7= X XL *kr и получим c учетом того, что p = (jcos/,£sin/)X *£ *, (59) ^(рЛ)«/(р,к) Тогда выражение (41) с учетом приближения (50) примет вид к = (к cos т, к sin тУхт LT , (60) ккг = (к cos г, к sin t^Xt LT LX^k cos г, к sin тУ = = ^2(z] cos2т + z2 sin2т^ = к"^А + 5cos2r), ^ ф'(к) = fexp(zpkr)x x (25д/р)- 5дЛ - ^k)- 5дДр + ^k))cZp = где AAX\ + Z2)/2 = (^i + 422)/2’ n _ (zi— z2) _ V^n— ЧтУУ + 4^(2(62) D =--------= , ^ (2 - exp(zt/^kkr)- exp(- idpkkT ))x x |ехр(/ркфдДр>/р = = —(1 - cos(tZ?.kkr Матрица Q имеет собственные значения X\ и Xi , которые являются корнями уравнения det(Q - zO = 0., где I – единичная матрица, и определяются выражениями, аналогичными (11): ^11 +922 +V(^n +^22)2 -4det0 Zi =------------"----Z------------------, ^1 +^22-<Чи + ^22)" -4det0 Z2 =----------------;-----------------• Vzi" 0 ° VzT cos p sin p -sinp eo%P ’ V Z2 ^n ^i2 v а якобиан преобразования dpx dpy J = dS d5 dpx dpy = 5detX"x = X . (63) Vdet0 dy dy Правая часть (61) получена с использованием известных тригонометрических равенств cos2 г = У(1 + С082г), sin2 г = У(1-со$2г). (64) С учетом (57)-(63) после преобразований выражение (51) примет следующий вид: - sin\k 1 Tdetg 2 d p A ) s in (A'2d p В с 0 s 2 т )) x (65) j^J0^dk^B^ (dGcosd) d5. Двумерные автокорреляционная функция и спектральная плотность флуктуаций связаны известным соотношением [1-4]: Ф дД^) = у JxSA^ Д V0 (^) dx-(66) Сделаем в выражении (65) замену переменной х = 5Geos9, а затем учтем выражение (66). Тогда /, х 2 ( 1 Ф, кк, т) = , -------- Ф х - sin(k2dp Ayin^k2dpBcos2r)). (67) Выражение (47) для условий слабого рассеяния (S4«S4w) после замены переменной (60) с учетом того, что якобиан преобразования co 2тг SL = ^etQ J |/:Ф z(k, ?)d rdk. (69) о о Подставим (66) в (69), сделаем замену переменной q = ^kj G cos ^) и воспользуемся табличными интегралами [16]: jsin(zcosx Jcos(zcosx )cos nxdx = к sin -™Jn (z) ’ )cos nxdx = л cos n (z)’ где z = (t/^Gcos^)" S, (71) n = 0, а также тем, что по определению 2л" [уФдДу> = 5д/о) = a2^ , (72) где у = k/(Gcos@\ Тогда выражение (69) с учетом обозначений (62) примет следующий вид: 711 + ^22 ) 2 J рактер распространения волны θ также определяют величину дисперсии флуктуаций фазы <7^ . В «дальней» зоне значение интеграла в правой части (73) становится пренебрежимо малым. В этом можно убедиться, подставив (73) в (49) и сопоставив полученное выражение с выражением (48). В результате будем иметьC«2^, что подтверждает достоверность полученного выражения (73). Конкретизируем (73) для случая, когда спектральная плотность флуктуаций электронной плотности Ф^М является гауссовской и подчинена следующему закону [1]: Ф^, 7) = °"1neCnexp(- ^7(2^0 Y )= (74) где Сд, – величина, которая определяется из условия (33), ko =NL». Используя табличный интеграл [16] (2z? -1)!! /7 2(2p)” Ap" где P = ^k'o , n = 1, из (29) для гауссовской спектральной плотности (74) получим 8^77' Подставив (76) в выражение (74), а последнее – в выражение (39) и воспользовавшись табличным интегралом [15] Jk1112 cxp(- ak^YR-Jo(yck)dk = о x'’+1/2 4Й> где a = (2^0) 2, v = 0, найдем, что Таким образом, как следует из выражения (73), индекс сцинтилляции ^4w определяется интегралом от произведения спектральной плотности флуктуаций фазы и фильтрующих функций. Фильтрующие функции в выражении (73) имеют аргументы, учитывающие наклонное распространение волны θ, а также анизотропию этих неоднородностей через геометрический коэффициент усиления G и элементы матрицы Q. Геометрический коэффициент усиления G и наклонный ха- V7(2/;,)2Azsec6'G BM H ) =---------7----------ехРГ x"ko ) • Полагая в выражении (78) x = 0, получим °"7 = ^7^ Y ^ sec 9 k^a1^ G . (79) Данный результат для случая изотропных неоднородностей, когда G = 1, совпадает с известным [17]. Тогда спектральная плотность флуктуаций фазы при подстановке (78) в выражение (66) и учете табличного интеграла (77), где a = kQ, v = 0, а также выражения (79), определится следующим выражением: при условии, что v + ///2 < 1, то при x = к/kg , ц = 3 , 1 - v = p/'Z из уравнения (29) для p > 3 получим 4ж0 к exp--т 4Z- , 1 Г(р2)к^N" ^г^р-зуну Подставив (80) в выражение (73) и воспользовавшись табличным интегралом [16] jexp(- 6x)cos(«x)^ (ex) t/x= Подставим (87) в выражение (85), а последнее – в выражение (39) и воспользуемся табличным интегралом [15] У (б2 + c2 - a2) + 4a2b2 + b2+c2—a2 я((б2 + c2 - a2)2 + 4a262) ^ + kg^ 4xkdg(xk^dk = ^(phY^ г^т^!) где Г nV V^ll “ ^22 ) +49i2 a = \dF G cos в) -------------------; b = \/Ak2, c = (d F G cos #)' ^n + ^“ ^, где v = 0, p +1 = p]Z . После математических преобразований найдем (x) = (Яг )2 Az sec 6G v \\x 7 v k0 2^"4Г-г^р-3^2) x (xkg ^'P"^^ K{p_2}l2 (xkg). (89) получим после преобразований t=2<7 , (83) Поскольку двумерная нормированная автокорреляционная функция должна удовлетворять соотношению [18] где (xk0^P2>KG-2>(xk^ (90) 2^"4У2г((/>-2)/2) F (2dFkoGcos0^ (dud 22 di2 из сопоставления (89) и (90) следует, что D = Yd F к gG cos б1)4^,I + ^?э У . Таким образом, выражение (73) для ^4 и при гауссовской спектральной плотности флуктуаций возможно представить в замкнутом виде (83)-(84). Рассмотрим случай, когда спектральная плотность подчинена степенному закону [3-4]: (Яг, )2 Az sec 0G f((p - 2)/2) (91) kg Г((/2-3)/2) Данное выражение совпадает с результатом, полученным в работе [4]. При подстановке (90) в выражение (66) спектральная плотность флуктуации фазы c учетом значения интеграла [15] ^w^K^at\TutJvVit^dt = ^AV,, W - ^ZW, , xpp ’ (85) (^+£2f 22(T(v + A4^)w2^ где ^ N – коэффициент, который должен быть где p = (p-2)/2, v = 0, определится следую- определен из условия (29), p – спектральный ин- щим выражением: декс. Поскольку согласно [16] »«,(<-)= Подставив выражение (93) в (73), получим й=2^, 1 ■' „-„/, I. Г((р-2)/2) Е(ьф) = Х 911 +^22 "*" а для p = 6 – следующий вид: где a и c определяются (82), а также с2 ^Дл b = ^0 • (95) у2 -У 1 Л —J ^Е2 Q, ф)8}(е(1, ^),1) аф. (103) При использовании интегрального представления функции Бесселя (70) и изменении порядка интегрирования выражение (94) примет после преобразований следующий вид: С=2< 1 Ft?/2) £ (р-2)/2 2^ Г((/2 - 2)/2) х Рассмотрим интегралы вида Величины С,(и,1) и ^(г/,!) в выражениях (101) и (103) определяются табличными интегралами [15] cos(x), (105) где Ci(x) и Si(x) – интегральные косинус и синус соответственно, под которыми подразумевают функции [19] Cz(x) = у + In х + I -------- at, (106) 0 1 \ rsin t . Si\x)= f----dt. (107) 0 t Интегрируя по частям правую часть выражений (97)-(98), получим у – постоянная Эйлера-Маскерони. Для p = 5 выражение (96) с учетом рекуррентных формул (99) и (100) примет следующий вид: , 2MCg,_2)/2(z/,6) Х ~ (р - 2) ’ (99) V2 - Л4и- —° ^ф Е^ф") ,2 . 2 ’Ao ko ^е^ф^ ^0 1/2 (108) аф. При этом cxnXi^bY sxrXihb^ определяются табличными интегралами [20] Формулы (99) и (100) являются рекуррентными. Выражение (96) с учетом соотношений (99)(100), (82) и (95) для p = 4 примет вид: -2C (uZz)cos(wZ)) - 2S (z/Z))sin(uZ>)), ^2 ^4w О"2 V 1 = vM ^^Ьф^з^е^фХ^ аф, (101) o\i=o ) где + 2C (ub)sin(ub) - 2S (z/Z?)cos(u6)), где С(х) и ЭД – интегралы Френеля, под которыми подразумевают функции [19]: Таким образом, когда спектральная плотность флуктуаций подчинена степенному закону, индекс ^4w определяется из выражений (101), (108), (103), для значений спектрального индекса p = 4, p = 5, p = 6 соответственно. Получить эти выражения в замкнутом виде затруднительно, но для их расчета можно воспользоваться численными методами интегрирования. Анализ (101), (103), (108) для SL с учетом (91), а также (83) с учетом (79) показывает на их прямо пропорциональную зависимость от величины ^„(^еУ ^0 . Это позволяет упростить вычисления и перейти к расчету нормированного индекса сцинтилляции С q(«O?72?) _ ^41 Кроме того, в указанных выражениях имеется зависимость *^4и: от аргумента ^рк^^ параметра G и угла 0 . При этом величина dF, как следует из выражения (45), также зависит от величины sec0 . Рис. 2. Зависимость нормированного индекса S^”'”^ от отношения радиуса первой зоны Френеля к внешнему масштабу неоднородностей для изотропных (а=1, Ь=1) и анизотропных неоднородностей (а=5, Ь=2) для гауссовской и степенной (при различных значениях индекса р) спектральной плотности флуктуаций Учитывая данное обстоятельство, сравнение значений ^ 4 и-' для различных спектральных плотностей флуктуации электронной концентрации при различных значениях параметра G и угла 0 целесообразно проводить в зависимости от произведения радиуса первой зоны Френеля для случая вертикального падения волны d^ = ^ХН ps I (2л:} =dF Jcos0 (114) и величины к^ > выраженной в градусах то есть от отношения радиуса первой зоны Френеля d^ к внешнему масштабу неоднородностей L^ . На рис. 2 в соответствии с указанными выше выражениями построены для изотропных и анизотропных неоднородностей зависимости индекса от отношения ^F I ^0 . Анализ графиков на рис. 2 для случая, когда азимут ф совпадает с углом магнитного склонения Vd ’ указывает на следующее. 1. Когда спектральная плотность флуктуаций электронной концентрации подчинена степенному закону, величина увеличивается с ростом спектрального индекса p. Это объяснимо, поскольку спектральный индекс показывает степень возмущения ионосферы. 2. Величина для гауссовского и степенного законов распределения спектральной плотности флуктуаций ожидаемо возрастает при увеличении радиуса первой зоны Френеля d^ относительно внешнего масштаба неоднородностей L0. 3. Индекс 4w увеличивается по мере усиления вытянутости неоднородностей (роста a и b) по сравнению с изотропным случаем ( a = 1,6 = 1 ). 4. При гауссовской спектральной плотности флуктуаций электронной концентрации график зависимости от отношенияd^p^LQ ведет себя примерно как при степенном законе с высоким спектральным индексом 0^6). 1 cy (norm ) _ Разработан метод вычисления индекса сцинтилляции на трассах распространения радиоволн в ССС при наличии анизотропных неоднородностей в возмущенной ионосфере. Метод основан на приведении квадратичной формы в аргументах автокорреляционных функции флуктуаций электронной концентрации и фазы к скалярному значению и учете этого при выполнении преобразования Радона и Фурье. С использованием данного метода получено выражение (73) для расчета индекса сцинтилляции при наличии анизотропных неоднородностей в ионосфере в виде интеграла от произведения спектральной плотности флуктуаций фазы и фильтрующих функций. Последние имеют аргументы, учитывающие анизотропию этих неоднородностей, а также наклонное распространение волны. Полученное выражение конкретизировано для гауссовской спектральной плотности флуктуаций в виде (83) и для спектральной плотности, подчиненной степенному закону со спектральным индексом в пределах от 4 до 6 в виде (101), (108), (103). Выражение (83) для гауссовской спектральной плотности имеет замкнутый вид. Для степенного закона выражения (101), (108), (103) представлены в виде, удобном для использования одного из численных методов интегрирования. В отличие от известных, полученные выражения позволяют оценить влияние сцинтилляций с высоким значением спектрального индекса (^^5), а также во всем диапазоне возможных значений отношения радиуса первой зоны Френеля к внешнему масштабу неоднородностей. 1. Маслов О.Н., Пашинцев В.П. Модели трансионосферных радиоканалов и помехоустойчивость систем космической связи // Приложение к журналу «Инфокоммуникационные технологии». Самара, 2006. – 357 с. 2. Singleton D.G. Saturation and focusing effects in radio-star and satellite scintillations // Journal of Atmospheric and Terrestrial Physics. Vol. 32, February 1970. – Р. 187-208. 3. Rino C.L., Fremouw E.J. The angle dependence of singly scattered wavefields // Journal of Atmospheric and Terrestrial Physics. Vol. 39, February 1977. – Р. 859-868. 4. Rino C.L. A power law screen model for ionospheric scintillation. 1. Week scatter // Radio Science. Vol. 14, № 6, November-December 1979. – P. 1135-1145. 5. Carrano C.S., Valladares C.E., Groves K.M. Latitudinal and Local Time Variation of Ionospheric Turbulence Parameters during the Conjugate Point Equatorial Experiment in Brazil // International Journal of Geophysics. Vol. 2012, Article ID 103963. – 16 p. 6. Booker H.G., Majidiahi G. Theory of refractive scattering in scintillation phenomena // Journal of Atmospheric and Terrestrial Physics. Vol. 43, Issue 11, November 1981. – Р. 1199-1214. 7. Шевченко В.А. Метод оценки влияния анизотропных неоднородностей в ионосфере на характеристики канала спутниковой связи // Вестник СКФУ. № 5 (38), 2013. – С 13-20. 8. Buckley R. Diffraction by a random phase screen with very large r.m.s. phase deviation. II. Twodimensional screen // Australian Journal of Physics. Vol. 24, 1971. – Р. 373-396. 9. Fremouw E.J., Secan J.A. Modeling and scientific application of scintillation result // Radio Science. Vol. 19, № 3, May-June 1984. – P. 687-694. 10. Carrano, C.S., Rino C.L. Split-step solution of the 4th moment equation for propagation through intense ionospheric disturbances // Proceedings of the International Conference on Electromagnetics in Advanced Applications (ICEAA 2011), Turin, Italy. – P. 469-472. 11. Wernik A.W., Alfonsi L., Materrassi M., Ionospheric irreqularities, scintillation and effect on systems // Acta geophysica polonica. Vol. 52, № 2, 2004. – P. 237-249. 12. Беллман Р. Введение в теорию матриц: М.: Наука, 1976. – 351 c. 13. Левин Г.Г., Вишняков Г.Н. Оптическая томография. М.: Радио и связь, 1989. – 224 с. 14. Гундзе Е., Лю Чжаохань. Мерцания радиоволн в ионосфере // ТИИЭР. Т.70, № 4, 1982. – С. 5-45. 15. Диткин В.А., Прудников А.П. Интегральные преобразования и операционное исчисление. М.: ГИФМЛ, 1961. – 524 с. 16. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. СПб.: БХВ-Петербург, 2011. – 1232 с. 17. Непп Д.Л. Расчет временных характеристик стохастических волн методом фазовых экранов // ТИИЭР. Т.71, №6, 1983. – С. 40-58. 18. Beniguel Y., Hamel P. A global ionosphere scintillation propagation model for equatorial regions // Journal of Space Weather and Space Climate. Vol. 1, Issue 1, 2011. – 8 р. 19. Янке Е., Эмде Ф., Леш Ф. Специальные функции. Формулы, графики, таблицы: М.: Нау-ка,1964. – 344 c. 20. Бейтмен Г., Эрдейи. Таблицы интегральных преобразований. Преобразования Фурье, Лапласа, Меллина. М.: Наука, 1969. – 344 c.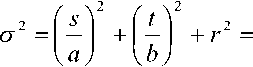
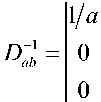
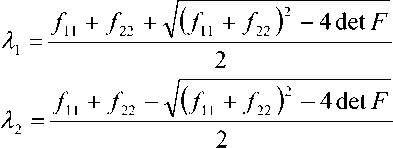
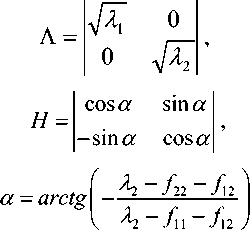
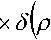
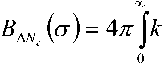
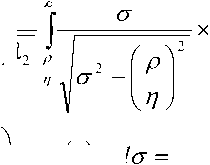
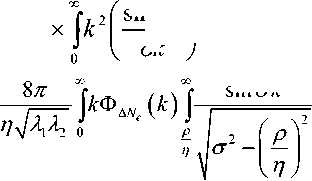
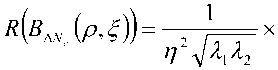
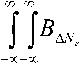
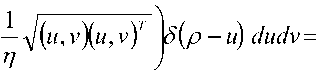
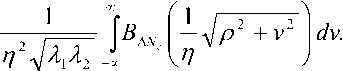
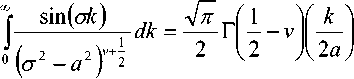
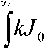

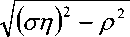
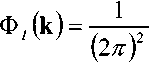
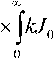
dkx dkv
J =
dk dk dkx dkv
= kdetX = k^]xAZ2 =k^detQ ,(^)
dr dr
примет следующий вид:
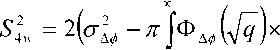
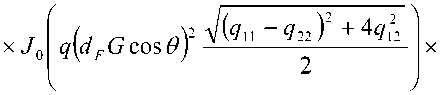
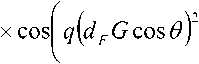
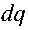
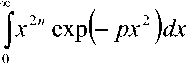
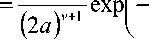
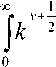
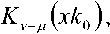
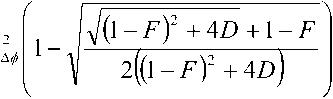
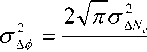
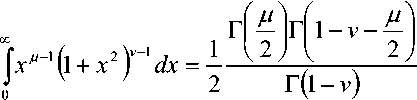
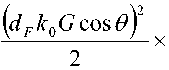
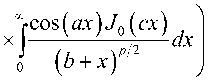
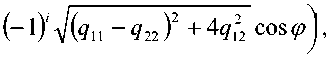
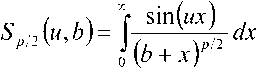
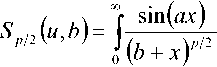
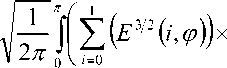
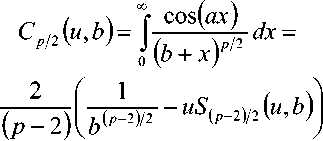
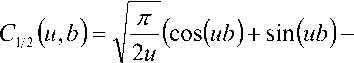
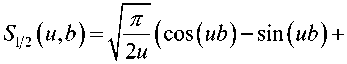
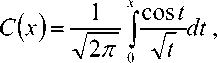
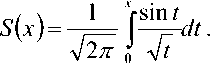
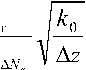
Список литературы Метод вычисления индекса сцинтилляции при наличии анизотропных неоднородностей в возмущенной ионосфере
- Маслов О.Н., Пашинцев В.П. Модели трансионосферных радиоканалов и помехоустойчивость систем космической связи//Приложение к журналу «Инфокоммуникационные технологии». Самара, 2006. -357 с.
- Singleton D.G. Saturation and focusing effects in radio-star and satellite scintillations//Journal of Atmospheric and Terrestrial Physics. Vol. 32, February 1970. -Р. 187-208.
- Rino C.L., Fremouw E.J. The angle dependence of singly scattered wavefields//Journal of Atmospheric and Terrestrial Physics. Vol. 39, February 1977. -Р. 859-868.
- Rino C.L. A power law screen model for ionospheric scintillation. 1. Week scatter//Radio Science. Vol. 14, № 6, November-December 1979. -P. 1135-1145.
- Carrano C.S., Valladares C.E., Groves K.M. Latitudinal and Local Time Variation of Ionospheric Turbulence Parameters during the Conjugate Point Equatorial Experiment in Brazil//International Journal of Geophysics. Vol. 2012, Article ID 103963. -16 p.
- Booker H.G., Majidiahi G. Theory of refractive scattering in scintillation phenomena//Journal of Atmospheric and Terrestrial Physics. Vol. 43, Issue 11, November 1981. -Р. 1199-1214.
- Шевченко В.А. Метод оценки влияния анизотропных неоднородностей в ионосфере на характеристики канала спутниковой связи//Вестник СКФУ. № 5 (38), 2013. -С 13-20.
- Buckley R. Diffraction by a random phase screen with very large r.m.s. phase deviation. II. Two-dimensional screen//Australian Journal of Physics. Vol. 24, 1971. -Р. 373-396.
- Fremouw E.J., Secan J.A. Modeling and scientific application of scintillation result//Radio Science. Vol. 19, № 3, May-June 1984. -P. 687-694.
- Carrano, C.S., Rino C.L. Split-step solution of the 4th moment equation for propagation through intense ionospheric disturbances//Proceedings of the International Conference on Electromagnetics in Advanced Applications (ICEAA 2011), Turin, Italy. -P. 469-472.
- Wernik A.W., Alfonsi L., Materrassi M., Ionospheric irreqularities, scintillation and effect on systems//Acta geophysica polonica. Vol. 52, № 2, 2004. -P. 237-249.
- Беллман Р. Введение в теорию матриц: М.: Наука, 1976. -351 c.
- Левин Г.Г., Вишняков Г.Н. Оптическая томография. М.: Радио и связь, 1989. -224 с.
- Гундзе Е., Лю Чжаохань. Мерцания радиоволн в ионосфере//ТИИЭР. Т.70, № 4, 1982. -С. 5-45.
- Диткин В.А., Прудников А.П. Интегральные преобразования и операционное исчисление. М.: ГИФМЛ, 1961. -524 с.
- Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. СПб.: БХВ-Петербург, 2011. -1232 с.
- Непп Д.Л. Расчет временных характеристик стохастических волн методом фазовых экранов//ТИИЭР. Т.71, №6, 1983. -С. 40-58.
- Beniguel Y., Hamel P. A global ionosphere scintillation propagation model for equatorial regions//Journal of Space Weather and Space Climate. Vol. 1, Issue 1, 2011. -8 р.
- Янке Е., Эмде Ф., Леш Ф. Специальные функции. Формулы, графики, таблицы: М.: Наука,1964. -344 c.
- Бейтмен Г., Эрдейи. Таблицы интегральных преобразований. Преобразования Фурье, Лапласа, Меллина. М.: Наука, 1969. -344 c.


