Метод вычисления информационных характеристик цифровых полутоновых изображений

Широкое распространение цифрового телевидения, фотографий, потоковое видео привело к росту количества передаваемой видеоинформации. Эффективное использование ресурсов при передаче и хранение видеоин- формации осуществляется с помощью алгоритмов сжатия.

Сжатие статических и динамических цифровых полутоновых изображений (ЦПИ) достигается за счет устранения избыточной информации. Существует два типа избыточности: 1) статистическая, связанная с корреляцией и предсказуемостью данных, которая может быть устранена практически без потери информации; 2) визуальная (субъективная), которая может быть устранена с частичной потерей данных.

Хороший алгоритм сжатия всегда должен минимизировать статистическую избыточность до определенного предела, который определяется энтропией входного потока данных. В случае одномерного потока данных энтропию до сжатия ЦПИ и после можно определить по хорошо известным формулам, приведенным, например, в работах Р. Фано [1], Р. Л. Страновича. Если информационный поток является многомерным, то вычисление энтропии вызывает определенные трудности.

Постановка задачи

В данной работе предлагается метод вычисления информационных характеристик в статических и динамических ЦПИ, представленных g -разрядными двоичными числами.

Чтобы получить объективные оценки статистической избыточности статических и динамических ЦПИ, необходимо построить их математические модели (ММ), адекватные реальным ЦПИ. С учетом статистических характеристик ЦПИ, в работе [2] разработаны ММ, на основе многомерных марковских процессов.

ЦПИ, представленное g -разрядными двоичными числами, можно разбить на g разрядных двоичных изображений (РДИ) [2].Если ЦПИ представляет собой двумерный марковский процесс с двумя значениями, то РДИ являются двумерным марковским процессом с двумя равновероятными ( P ₁ = P ₂) значениями.

Рассмотрим способ вычисления статистической избыточности для одномерного информационного потока данных при передаче элементов одной первой строкиРДИ, которые образуют группыимпуль-сов одинакового знака (цуги) случайной длины.

Интерес представляет средняя длина цугов χ , которая связана с элементами матрицы вероятностей переходов (МВП) одномерной цепи Маркова с двумя значениями простым соотношением [2]:

i^l)-1 2 P i ⁽ l) i^l)- i-i ^l) m ⁿ ii = ¹ ( l ) , ⁿ j = ^{1 n} ii , ⁽¹⁾

где 1 n( ) ( i , j = 1,2, i * j ) — элементы МВП по строке ¹ П = |^п^ ; l = 1,J .

Если элементы l -го РДИ в строке некоррели-рованы ( 1 п ⁽ ) = 0,5), то х ( l ) = 2, количество информации в элементе максимально и будет составлять один бит.

Для средней длины цуга х ( l ) = 10 и вероятности п ^{( l} ) = 1 - n j ) = 0,9, ( i = 1,2), количество информации в одном принимаемом элементе строки l -го РДИ равно:

I ( “ i , j | A, j + 1 ) = - log ⁿ( l ) = - log ^0,9 =

=0,152 дв.ед.

При этом статистическая избыточность формации в одном элементе равна

^ I ⁽ ^ i , j ^, M i , j + 1 ) = I max ^— I ⁽ ^ z, j |z^ i , j + 1 ) =

= 1 – 0,152 = 0,848 дв.ед.

ин-

Таким образом, по аналогии с (2)-(3) можно найти статистическую избыточность в элементах одной строки РДИ при любой корреляции между значениями соседних элементов.

Для вычисления статистической избыточности статического РДИ, представляющего собой двумерный информационный поток данных, в качестве ММ РДИ выбираем одностороннее марковское случайное поле (ОМСП), называемое также двумерной марковской цепью на несимметричной полуплоскости (НСПП) [2] (см. рис.1).

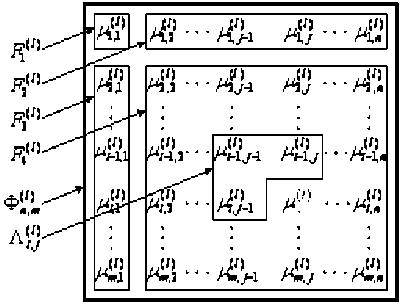
Рис. 1. Области ОМСП с окрестностью из трех элементов

Для того чтобы { « ( lj } являлось ОМСП, необходимо выполнение условия

P ( ^ i , j| М к _Д ; ( k , q ) e^-, j ) = PH j\ M k,q ; ( k , q^ ^ ^л i, _j ) . ⁽⁴⁾

Множество элементов Λ _i,j , называемое окрестностью элемента μ _{ij ,} лучшим образом удовлетворяет условию каузальности, имеет вид [2]

Л(1) -L<1) z/d) z/d)

^Л i,j = I^м i,j - 1 , H i - 1,j , H i - 1, j - 1 ) ■           ⁽⁵⁾

Тогда все множество элементов ОМСП с окрестностью (5) можно условно разделить на четыре части, каждая из которых имеет вид (рис.1) [2]:

л(1).

i,j

0                        при ( i , j ) 6 F ¹ ) ;

_{( i — 1, j )} ,                       при ( i, j ) 6 F ^ ) ;

{⁽ i , j ^{-1 )}} ,                       при ( i, j ) ⁶ F¹ ) ;

{ i, j ^{- 1 )( i -} 1, j ^{)( i -} 1, j ^{-1 )}} , при ^{( i} , j ) ⁶ F 4 ⁽ l ) •

Статистическая избыточность, свойственная ЦПИ, присуща также и РДИ, на которые оно разбивается. На рис. 2 представлен фрагмент двумерного бинарного изображения, соответствующего области f 4 ) НСПП (см. рис. 1), где приняты следующие обозначения:

^v 1 ^=μ i,j-1 ^{; v} 2 ^=μ i-1,j ^;

^v 3 ^{= μ} i-1, j-1 ^{; v} 4 ^=μ i,j

Рис. 2. Фрагмент двумерного бинарного изображения

Будем считать, что l -е РДИ ( 1 = 1, g ) представляет собой случайное марковское поле с разделимой автокорреляционной функций вида [2]

Для определения статистической избыточности в РДИ найдем сначала количество информации в элементе v 4 j l ) относительно его окрестности A j = . ' , v2 ' , v2 ' } .

Количество информации, содержащееся в элементах v ^{( l} ) , v 2 ) , v⁽) l -го РДИ относительно элемента v 4 l ) , представим в виде [2]:

I ( v 4 l > ;v 3 l );v 2 l ) ;v fl > ) =

= log _p^(vU L ^V2^l.⁾L^V£jL^V£. ⁾)   ’    (9)

^P ( V 1 ^l^^p (V^ p (Vp") p ( V4^)

где

p(vi()), i = 1,4 - априорные плотности ве- роятностей значений элементов l-го РДИ; p(/(l), v2), v3^), v4(l)) — совместная плотность вероятности значений элементов изображения.

Количество взаимной информации между элементами, входящими в окрестность Л"и = V i l ) , v 2 l ) , v 3 ( l ) } , по аналогии с (9) запишем в виде

I (v 3(l) ;v 2(l) ;v 1(1))= p (v 1(l), v 2l), v 3(l))     ■      (10)

^{0 8} P ^{( v} 1 ⁽ l ) M^V 2 ⁽ l ) ) P ^{( v} 3 ⁽ l ) )

Количество информации в элементе v 4, ¹ ) ( 1 ) ( 1 )

относительно элементов ν ₁ , ν ₂ найдем как разность выражений (9) и (10). Удалив информацию между элементами v 4 ) и v 3 ( l ) , получим:

Р ( l ) ^{( k} , g ) = ^с _А 2 exp { — ^a i ⁽ l )|g| - ^a 2 )| k } ,   (7)

2 ^( l ) ^( l ) где σ _μ –дисперсиясигналаизображения; α ₁ ,α ₂

– множители, зависящие от ширины спектральной плотности мощности случайных процессов по горизонтали и вертикали. В этом случае РДИ описывается вектором p ( ^ j ) = { P i , P 2 } начальных вероятностей и двумя МВП по горизонтали и вертикали РДИ:

1 ^{( l} ) 2 ( l )

I V ?v2),v22' ) =- log ^^ ,  (11)

π _ii

где n ii , i , j = 1,2; i ^ j - элементы матрицы

³ П = ¹ П • ² П =

3 27 ⁽ l )

^π 11

3 27 ⁽ l ) π ₂₁

3 27 ⁽ l )

^π 12

3 27 ⁽ l ) ■ π ₂₂

¹ П ^{( l )} =

² П ^{( l )} =

1л ^{( l} ) π ₁₁ 1л ^{( l} ) ^π 21

1л ^{( l} )

π ₁₂

1Л ^{( l} ) ’

^π 22

2Л ^{( l} ) ^π 11

2Л ^{( l} ) ^π 21

2Л ^{( l} ) ^π 12

2Л ^{( l} ) ^π 22

l ∈ g .

Для элементов l -го РДИ, принадлежащих области f 4 ) (рис.1), количество информации между элементом v 4д ) и различными сочетаниями значений элементов окрестности Л А можно определить по матрице П (13):

П =

α1

α2 α3

α4

β 1

β 2

β 3

β 4

а ’ ^а 2 а ’ а 4 в ; в 2

в 4

πii πii ii

71- 71- ij ij

3 πii ii ii

^{3 π} ii

πij πij ii

πij πij ii

^π ii ^π ii

3 πii ij ij

^{3 π} ii

ii ii ii

ν ₁ ν ₂ ν ₃ → ν ₄

000 → 0

111→0

111→1

000→1

где а ‘ = 1 - a i .

Из анали за элементов матрицы П следует, что ai = в i ( i = 1,⁴ ) , а 4 = а ’ и в ₄ = в 1 , что позволяет сократить количество вычислений.

Например, при одинаковой корреляции по горизонтали (строкам) и вертикали (столбцам) РДИ равной 1 п i - - ) = ² п i - - ) =0,9 и одинаковых значениях элементов окрестности Л^ равных M 1 количество информации в элементе v *4 ) = M 1 минимально и будет составлять

I V 4 I'

^V 1 , V 2 ) = ^- log

( Ч (l ) ² к (l ) ) ⎜ ^π ii ^π ii ⎟

⎝ π ii

⎠

-

⎛ log ⎜⎜

0,9 ² _⎟⎞

⎝ 0,82 ⎟⎠

= 0,0177 дв.ед.

При отсутствии корреляции по горизонтали и вертикали l -го РДИ ( 1 п( l ) = ² п( l ) =0,5) количество информации в элементе v) равно

I ( ^V 4 ^V 1 , ^V 2 ) =- log

/ „ 9 Л ⎛ 0,5² _⎟⎞ _⎝ 0,5 ^⎟_⎠

= 1 дв.ед. (15)

Сравнивая выражения (14)и (15),можно опреде-

( l )

лить статистическую избыточность в элементе ν ₄ :

AI V 41

V 1 , v 2 ) = 1 - 0,018 = 0,982 дв.ед.

Статистическая избыточность в элементе ν ₄ зависит от комбинаций значений элементов окрестности Л ¹ ! . Зная элементы МВП (13), можно вычислить среднюю статистическую избыточность l -го РДИ. Статистическая избыточность элементов g -разрядного ЦПИ складывается из статистической избыточности, содержащейся в элементах каждого из g РДИ вида

A I _z = ^L A I (l ) .

1 = 1

Предельный коэффициент сжатия ЦПИ будет равен отношению максимального количества информации в элементе исходного ЦПИ I _max к минимальному количеству информации g РДИ I _Σ :

K c = ^I max >  1 .

I _Σ

Рис. 3. ЦПИ «Airplane»

На рис. 4 представлено распределение значений элементов МВП по горизонтали и вертикали РДИ ЦПИ «Airplane» (см. рис.3). На рис. 5 приведена зависимость статистической избыточности в l -м РДИ от номера разряда ЦПИ «Airplane».

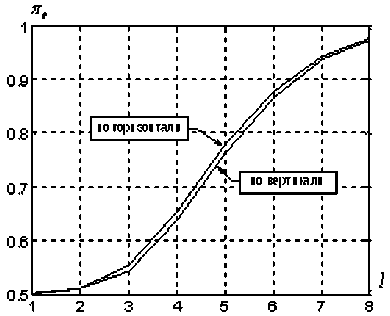
Рис. 4. Распределение усредненных значений элементов матриц вероятностей переходов

Для приведенного примера предельный коэффициент статистического сжатия (17) статического ЦПИ «Airplane» составит 2,5.

Статистическую избыточность элементов динамических РДИ, представляющих собой последовательность РДИ, можно найти, если восполь-

зоваться ММ, полученной в работе [2] на основе представления последовательности РДИ двоичным трехмерным марковским процессом.

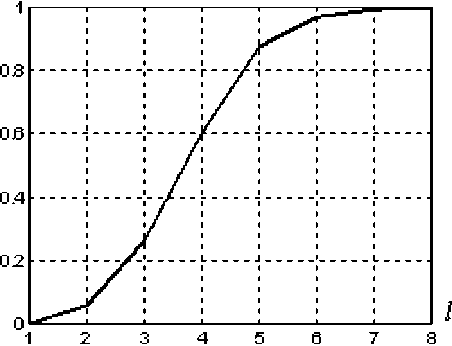
Рис. 5. Зависимость статистической избыточности в l -ом РДИ от номера разряда ЦПИ

На рис.6 приведен фрагмент пространственно-временной модели последовательности РДИ, принадлежащей областям fA ) и F ^ lk _{- 1}) в к -м и (к - 1) -м кадрах с окрестностью элемента v 4 вида

_Л(1 ) О) _V( 1 ) _V( 1 ) /1 ) /1 ) _V<1 ) 3)} ₍1₈₎ ^л ук = ^v 1 , ^v 2 , ^v 3 , ^v 1 , ^v 2 , ^v 3 , ^v 4 J’ ⁽¹⁸⁾

где приняты обозначения:

• ^v 1 ⁽ l ) = ^ ( i, j - 1, ^k ) ^v 2 ⁽ l ) = Ц ^{( i} - 1, j, ^k )

• V 3 ( ) = ^ ( i - 1, j - 1, k ) ,

• V \ ^l ) = A ( i , j - 1, k - 1 ) , v 2 ( l ) = A ( i - 1, j , k - 1 ) , v 3 ( l ) = A ( i — 1, j — 1, k — 1 ) , v 4 ( l ) = A ( i , j, k — 1 ) -

• При этом количество информации, содержащейся в элементах окрестности л(1) _U1) V(1) V(1) VM) v.() VM) VM)

^Л ijk = Г 1 , ^V 2 , ^V 3 , ^V 1 , ^V 2 , ^V 3 , ^v 4 J относительно элемента V 4 ) , можно определить из выражения вида:

Av (i WM^l W^l M MMM>)-I v i ;^v 2 ’ ^v 3 ;^v 4 ^V1 ^{, v} 2 ^,v3 ^{, v} 4 =

P v ?) , V ^{( l} ) , v ^{( l} ) , v ^{( l )} , v ‘ ^{( l )} , v Al ) , V'^ , V Al ) ) (19) log ---- r^—r^—;-----"

П p(v j ^l ) ) • П p(v ' ^{( l )} ) i= 1            i= 1

Информация, содержащаяся между элементами РДИ, входящими в окрестность Л j , может быть вычислена аналогично (19):

Av (1 )-v^¹ )'_V(l)-v'(l)-v'(l)-v'(l)-v'(i )}-

I v 1 ; V 2 ; V 3 ; V1 ; V 2 ; V 3 ; V 4 = lo PviMMPviPiVi^^   1" (20)

⁸          пП p(v⁽ ) ) • II pA\^¹ ) )

i= 1              i= 1

В данном случае количество информации в элементе V4-l ) относительно элементов _Л( l ) _L(l ) _v(l ) _v(l ) _vAi ) _v.^(l ) _v.^(l ) _v.^(l )l найдем Λ _ijk = ν ₁ , ν ₂ , ν ₃ , ν ₁ , ν ₂ , ν ₃ , ν ₄ надем как разность выражений (19) и (20). Удалив информацию, содержащуюся в элементах l -го РДИ v₃ ^{( l} ) , Vj ^{( l} ) , v 2^{( l} ) , v 3^{( l} ) относительно элемента v 4^ ), получим

I V «"Pl > , V < l > , v ;<" ) =

= - log⎜1 -

⎝

¹    ( l ) ² ( l ) ⁴ ( l ) 7    ( l n

^π ij ^π ij ^π ij ^π ii ⎟

3    ( l ) 5    ( l ) 6    ( l )

π _ii π _ii π _{ii ⎠}

,

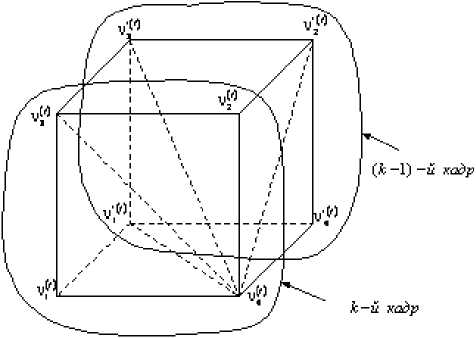
Рис.6. Фрагмент пространственно-временной модели

где q n j ) ( i , j = 1,2; i Ф j ; q = 1,7 ) - элементы матриц вероятностей переходов ¹П – по горизонтали; ²П - по вертикали; ⁴П – по кадрам;

³ n ^{( l} ) = 1 n ^{( l} ) -2 П ^{( l} ) ■

⁵ n ^{( l} ) = 1 n ^{( l} ) -4 П ^{( l} ) ■      ⁶ П ^{( l} ) = ² П ^{( l} ) - ⁴ П ^{( l} ) ■ (22)

7 n ^{( l} ) = ³ n ^{( l} )- ⁴ n ^{( l} ) = 1 n ^{( l} ) -2 n ^{( l} ) -4 n ^{( l} ) "

Количество взаимной информации между элементами окрестности (22) и элементом v _{4 k} ^{( l} ) при одинаковой корреляции элементов по горизонтали, вертикали и кадрам (см. рис. 1, область F 4 _k ( l ) ) может быть определено по матрице П*

П* =

ν ₁ ν ₂ ν ₄ ′ν ₃ ν ₁ ′ν ₂ ′ν ₃ ′ → ν ₄

′

*

^а 1

*

^а 2

^а 1

^а 2

* а 8

в1в 2

а 8* в’

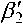
в 8^*

*

в 8*

0000000 → 0

1000000 → 0

1110000 → 0

1111111 → 1

0111111 → 1

0001111 → 1

I⎜ ν ₄ ν ₁ ,ν ₂ ,ν ₄

-

log ^⎜ 1 ⎝

-

^π ij ^π ij ^π ij ^π ii ⎟^⎞

356   ⎟

^π ii ^π ii ^π ii ⎠

= 0,002 дв. ед.

Статистическая избыточность для приведенного примера составит

где элементы матрицы П* удовлетворяют усло-

вию нормировки

а* + а '* = 1 ; i = 1,8; а * = в * ■

Элементы матрицы П можно определить те-

перь как

*

a 1 = a ₈ =

= в 1 = в 8 ;

*,*

a 2 — a 7 —

— в 2 — в 7

*

^a 3 = ^a 6 =

= в 3 = в 6 ;

a ₄ = a ₅ =

= в 4 = в 5 ;

-

1      ^(l ) 2      ^(l ) 4      ^(l ) 7      ^(l )

^π ij      ^π ij ^π ij ^π ii

3-rr  ( l ) 5-rr ( l ) 6-rr ( l )         ;

π _ii π _ii π _ii

A I ( ^v 4 ) = I max ^{( v} 4 | ^v 1 , ^v 2 , ^v 4 ) ^- - 1 ( v 4 V 1 , v 2 , v 4 ) = 0,998.

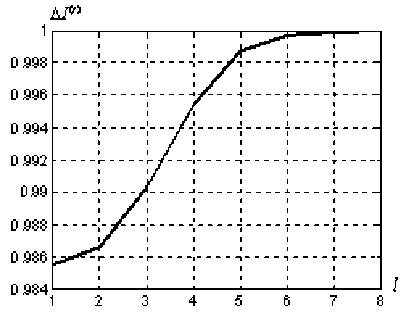
Рис. 7. Зависимость статистической избыточности в l -ом РДИ от номера разряда ЦПИ

π _ii

( l ) 2      ( l ) 4      ( l ) 7 ( l )

^π ij ^π ij ^π ij

3„   ^{( l} ) 5      ^{( l} ) 6 ^{( l} )       ;

^π ij ^π ij ^π ii

*        ,*

a ₅ = a ₄ =

= в 5 = в 4 ;

^a 6 = ^a 3 =

= в 6 = в 3 ;

a ₇ = a 2 =

= в 7 = в 2 ;

-

1      ^{( l} ) 2      ^{( l} ) 4      ^{( l} ) 7      ^{( l} )

^π ii      ^π ij      ^π ij      ^π ij

3;r ^{( l} ) 5      ^{( l} ) 6      ^{( l} )

^π ij ^π ij ^π ii

*

,*

a 8 = a 1 =

= в 8 = P i

^π ij

( l ) 2      ( l ) 4      ( l ) 7      ( l )

^π ij ^π ij ^π ii

3^ ( l ) 5^ ( l ) 6^ ( l ) π _ii π _ii π _ii

.

В общем случае матрицы ¹ П ^{( l} ) , ² П ( l )

;

и

⁴ П ( l )

априорно известны и определяют корреляционные связи между двоичными элементами l -го РДИ по горизонтали, вертикали и времени (кадрам) в последовательности РДИ.

( l)_2_ ( l)_4_ ( l )

Пусть π _ii = π _ii = π _ii = 0,9, тогда если все элементы окрестности Λ _ij_k имеют одинако- ( l )

вые с ν ₄ знаки, то количество информации в

( l )

элементе ν ₄ относительно элементов окрестности будет составлять

Если элементы в последовательности РДИ независимы, то положив q _n j ) = 0,5 ; I ( V 4 ) = logo,5 = 1 дв. ед., а относительная статистическая избыточность отсутствует, то есть A I ( v 4 ) = 0.

На рис. 7. приведена зависимость статистической избыточности в l -ом РДИ от номера разряда в динамическом ЦПИ «Airplane» ( ⁴ π ii ⁼ 0^,99 )^. Для приведенного примера предельный коэффициент статистического сжатия динамического ЦПИ «Airplane» составит 182.

Таким образом, в данной работе получены выражения для вычисления среднего количества информации в одном элементе в статических (14) и динамических (21) ЦПИ и рассмотрены примеры вычисления статистической избыточности и предельного статистического коэффициента сжатия статических и динамических ЦПИ.