Метод задания положений узловых точек, определяющих конверты теней при различных направлениях солнечных лучей и углах поворота зданий

При планировании местоположения жилых сооружений на заданной территории необходимо учитывать их взаимные положения теней. Это необходимо для оценки инсоляционного режима территорий застройки и помещений [1, 2]. В работах [3–6] приведены геометрические методы определения контуров теней зданий и в целом инсоляции заданного участка площади застройки.

Методика определения положений зданий на основе использования обобщенных координат и синтеза их малых движений предложена в работах [7, 8]. При этом способе на каждой итерации исследуется положение теней относительно зданий. Поэтому наиболее эффективным способом при вычислении непрерывной инсоляции при указанных расчетах является задание контура теней набором узловых точек для определенных углов ориентации зданий относительно направления восток – запад и угла наклона солнечных лучей. В данной работе предложен автоматизированный способ определения контура теней зданий, имеющих прямоугольную, П-образную формы или форму с криволинейными участками зданий для произвольных значений указанных углов.

Рассмотрим на рис. 1 в качестве примера изображения контуров почасовых теней для различных углов поворота α солнечных лучей зданий, имеющих различную форму на горизонтальной проекции. Продолжительность инсоляции определенного фрагмента Ѳ i-го здания в течение заданного интервала времени с определенным приближением будет задавать количество пересечений этой области (данные области на рис. 1 обозначены и _) и т. п.)с выпуклыми областями Д;;- и Д-' почасовых теней в течение светового дня, где параметры i и j соответственно задают номер здания и номер почасовой тени. Для П-образного здания количество участков, заданных прямоугольниками (используемыми для определения общей тени жилого сооружения) на горизонтальной проекции, будет равно трем, а количество фрагментов – соответственно пяти. При этом тень каждого из трех прямоугольников задают пятиугольники Д-^ [7, 8]. В общем случае эти пятиугольники могут накладываться друг на друга, и общая форма тени здания при этом с течением времени изменяется (см. рис. 1). Количество выпуклых областей пятиугольников Д^ зависит от числа l прямо- угольников, определяющих горизонтальный очерк зданий. Например, для здания с криволинейным фасадом количество прямоугольников принято равным пяти. На рис. 1 солнечные лучи, соответствующие полдню и располагающиеся в плоскости Γ, наклоненной под углом γ = 35° к горизонтальной плоскости, соответствуют дню осеннего и весеннего равноденствия. Каждая отдельная область тени Ду может быть задана пересечением областей λj (полуплоскостей), определяемых прямыми линиями [9]. Индекс k указывает время, определяющее положение почасовой тени. Методика аналитического задания указанных выпуклых областей почасовых теней изложена в работах [7, 8].

Анализ построения теней показывает, что при изменении угла наклона солнечных лучей координата у узловых точек F_ki тени не изменяется (см. рис. 1) (параметр ki определяет номер узловой точки тени 1 ≤ ki ≤ 5). Значения указанной координаты у вычисляется по формуле:

у = Н • tg⁽90 ° - Y)+y FG , (1) где Н – параметр, определяющий высоту здания, γ – угол наклона плоскости Γ к горизонтальной плоскости проекций, y_FG - координата у точки здания, для которой определяется тень в неподвижной системе координат. Для автоматизированного расчета положений конвертов теней определим функции изменения координаты х узловых точек F 1 "F 5 областей Ду, от углов а и в (см. рис. 1). Угол β задает наклон здания по отношению к направлению восток – запад (см. рис. 1).

В работе [8] выполнено соответствие узловых точек Fki контуров теней Д^ пятиугольников точкам контура здания на горизонтальной проекции для различных моментов времени, а именно 8, 10, 12, 14 и 16 часов. Данные точки могут быть использованы при автоматизированном расчете положения областей Д^ при синтезе движений зданий с целью определения минимальной площади застройки и c обеспечением заданных требований инсоляции [7]. Как видно из рис. 1, в различные моменты времени текущие точки Fki областей Ду, например точки F®, F^0, F^, F^4 и F^6, определяются различными точками, а именно А и В, задающими горизонтальный очерк здания. Верхние индексы 8, 10 и т. д. обозначений точек на рис. 1 задают время, соответствующее почасовой тени.

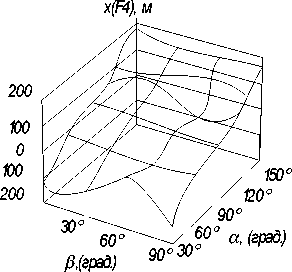
На графиках рис. 2 отображены зависимости значений текущих со временем координат х (в метрах) точек F ₂, F ₃ и F ₄ для одного из прямоугольников А ₁ В ₁ С ₁ D ¹ ₁ горизонтального очерка здания (располагающегося с левой стороны), имеющего высоту пятьдесят метров при различных значениях углов α и β i .

Координата х узловой точки тени, полученной от заданной точки здания, может быть вычислена по формуле

Х НI t .    . sin а sin у I + xFG tg(arcsin cos а /

где xFG - координата x точки здания в неподвижной системе координат, для которой определяется тень. Формула (2) определяется следующими три- а

в

С

dh

D 2⁸

α0

z0 (м)

А2 =B2

50 C 2 =D 2

А 2в =В 2в С ^2в =D ^2в

H 2 =I 2

в

h

z0 (м)

)

Γ

₂ 12 =В 12

10    10 10 10

F₃ 8 =В 8 F₄₈=С₈   F₃ 10 =В 10 F₄ =С

F₂ 14 =

14 3 =

=A8в

-

λ 1

10    10

2 =A

β

λ 1⁺

8 Δ₁₁

F 5 =G 1в

- 100          161

_{12 1} 10_{1 2     3     4}

₅I 1

200      х 0 (м)

E 1в

Рис. 1. Изображения конверта теней зданий, соответствующих 8, 10, 12, 14 и 16 часам

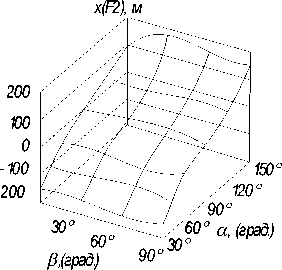
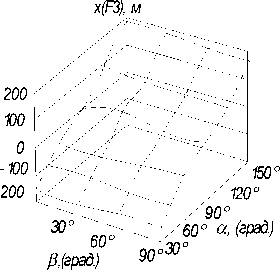
Рис. 2. Графики функций x F2 _{+ F4} = f 1-3 (а,в) для различных значений Н = 50, 100 и 150 м

гонометрическими функциями, полученными из анализа рис. 1:

^hh ft = a^sina; nn = a •sin a sin у; sin a = —;

b sin a sin v                H b = a^cosa; a = arsin(------); tga = - cos a                 x

Однако зависимость (2) не может быть использована для определения координат текущих узловых точек F 2 , F 3 и т. д. тени, так как положения данных точек (например, точки F 2 ) определяется различными точками горизонтального очерка здания. Для определения координаты х промежуточных узловых точек F_ki удобнее всего использовать полиномы третьей степени, отражающие зависимости, представленные на рис. 2 [10–12]. Уравнения полиномов третьей степени имеют следующий вид [11]:

х F2 = а^а3 + a22a2 + аз2а + aj2, xf3 = af3a3 + af3a2 + af3a + af3.          (3)

Коэффициенты afl,af2... af4 для определенно заданного значения угла βi получают при подстановке координат четырех точек Fki, построенных гра- фическим путем. Например, для определения первого уравнения системы (3) необходимо подставить в данное уравнение значения координаты х точек А8, А10, В14 и В16 и решить систему из четырех уравнений с четырьмя неизвестными. На основе определения коэффициентов af2 ^ af2 для четырех различных углов βi можем установить зависимости af34 = /1-4(вi) этих значений от угла вi• Для нахождения указанных зависимостей используем другие полиномы третьей степени:

af3 = bf3 в3 + bf3 в2 + bf? р, + ЪЦ, af3 = bfl S3 + b2f23 в2 + bfl в, + bF3 , af3 = bH S3 + b3f23 S2 + bH Pl + bH, af3 = bfl S3 + b4f23 P2 + b4f33 Pl + b44.

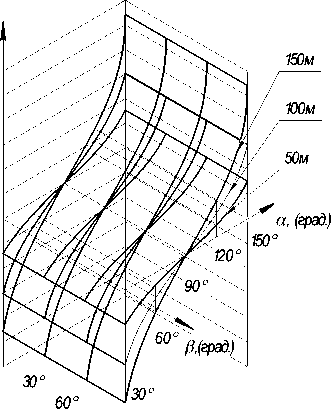
Использование полиномов (3) и (4) позволяет вычислять координату х узловых точек Fki конвертов теней для произвольных значений углов α и βi для точек прямоугольников, задающих в совокупности горизонтальный очерк зданий. На рис. 3 выполнено изображение функций (3) и (4) для точек F2 и F3 для трех различных значений парамет- х(F2), м

-100

-200

-300

-400

-500

90 °

а)

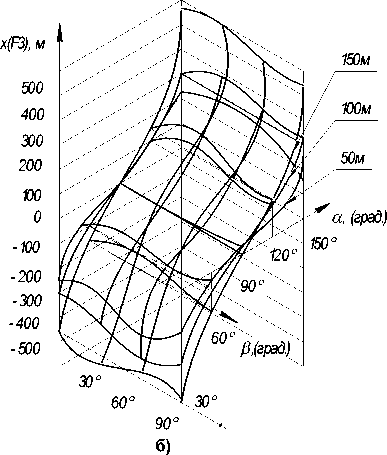
Рис. 3. Графики функций а) хF2 =f(α,β), б) хF3 =f(α,β) для значений Н = 50, 100, 150 м

ра Н , а именно 50, 100 и 150 м. Пример полученных значений коэффициентов полиномов (4) для узловой точки F ₃ при Н = 50 м для прямоугольника А 1 В 1 С 1 D ¹ 1 представлен в таблице.

Алгоритм определения взаимного положения зданий и конвертов теней представлен на рис. 4. Приняты следующие обозначения: 1 – ввод данных i = 1,imax– максимальное число размещаемых зданий, β1 = 0, β2 = 0, …βi = 0 (βi – угол поворота i-го здания относительно направления восток – запад), k1 = 0, k2= 0 … ki = 0, (ki1, ki2, …, соответственно число пересечений первого, второго и т. п. фрагментов i-го здания с конвертами теней), kimax – максимально допустимое число пересечений области фрагмента здания и теней, заданное в соответствии с нормативами инсоляции, kkimax – максимальное значение количества фрагментов i-го здания (для тестового задания - kk1max = 5, kk2max = 8,kk3max = 2), α = 0, βimax =175; 2 – смещение зданий по критерию минимизации объема движения по вектору обобщенных скоростей [7]; 3 – определение коэффициентов полиномов a1F2, a2F2,…b11Fi, b12Fi… в соответствии с базой данных для каждого жилого сооружения для значений углов α и βi (база данных значений коэффициентов определяется заранее); 4 – вычисление координат текущих точек Fki конвертов теней в подвижных и неподвижных системах координат в соответствии с углами α и βi (3) и (4); 5 – вычисление коэффициентов уравнений прямых, проходящих через точки Fki, задающие полуплоскости λ, заданные точками Fki, Fki+1 i-го здания [9, 10]. Определение областей Д-k на основе булевых операций теории множеств [9]; 6 – определение пересечения kk-го фрагмента горизонтальной проекции i-го здания с областями Д-k; 7 - пересечение есть; 8 – ki = ki+ 1; 9 – kk = kk + 1; 10 – kk >kkmax; 11 – i=i + 1, kk= 0; 12 – i>imax; 13 – ki >kimax; 14 – α >150°; 15 – положение i-го здания при текущем значении угла βi не удовлетворяет нормативам продолжительности инсоляции; βi = βi + 5º; 16 – βi > βimax; 17 – положение всех зданий удовлетворяет продолжительности инсоляции; 18 – qit = qit+∆qit (qit – значения обобщенных координат); ∆qit – приращение обобщенных координат [7]. Определение нового положения зданий, при котором выполняется условие £ft=3 q^ < Zft=3 9it-i, где Qit и qtt-1 — значение обобщенных координат соответственно на текущем и предыдущем шаге расче-

Значения коэффициентов полиномов (4), позволяющих определить координату x узловой точки F 3

Обозначение точек	Коэффициенты полиномов
	bl^bi^	bl^-b^	b lk^ b lk	hFki — hFki b 41    • b 44
F 3	-0,0026 0,2453	-0,0022 0,2068	-0,0019 0,1877	0,0003 -0,0323
	-5,3489 9,7373	-4,4998 8,1898	-4,0901 7,4453	0,6900 -1,2576

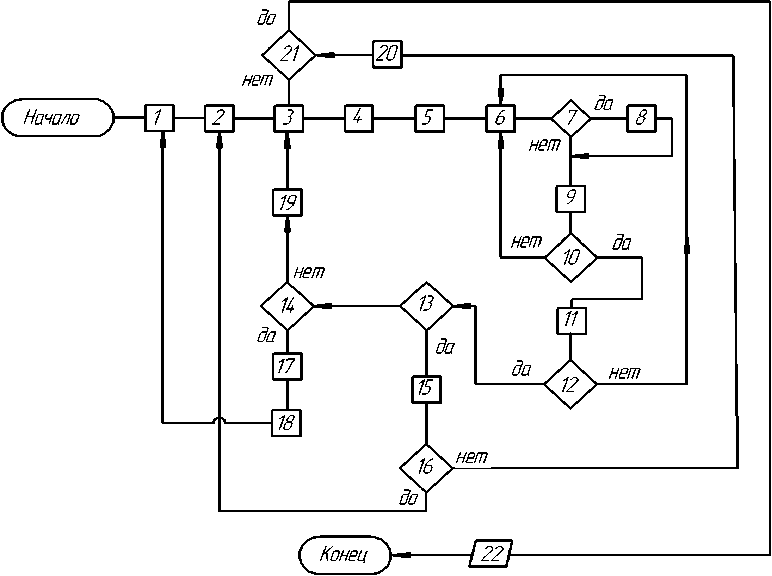
Рис. 4. Схема алгоритма определения продолжительности инсоляции на основе анализа положения областей фрагментов зданий и контуров теней

тов, it - номер обобщенной координаты (для рассматриваемого случая общее число обобщенных координат it = 6); 19 – α = α + 5º; 20 – вычисление новых значений приращений ∆qit [7], не соответствующих критерию минимизации объема движения; 21 – все возможные значения вектора приращений обобщенных координат ∆q_it исследованы [7]; 22 – вывод окончательных значений обобщенных координат q_ii , задающих положения зданий, при которых соблюдаются нормативы инсоляции.

На рис. 5 представлены результаты одного из этапов моделирования перемещения зданий с выполнением условий Е^ з q_lt <  ^ц.-^ q tt-i и Δ ^k ij Ѳki на каждом шаге расчетов. Моделирование осуществлялось с использованием САПР ACAD и алгоритмического языка программирования AutoLISP. При моделировании на каждой итерации происходит уменьшение суммы значений обобщенных координат qit , а следовательно, и площади застройки. На рис. 5 обозначения q 1 , q ₂,… q ₆ задают отрезки, определяющие первоначальные значения обобщенных координат. Контуры Р ₁, Р ₂ и Р ₃ задают первоначально заданное положение зданий и их фрагментов. Точки О ₂, О ₄ и О ₆ задают начало подвижных систем координат, связанных со зданиями. Соответственно контур, заданный точками D 1 , D 2 , … и т. п., определяется линейными объектами, в качестве которых выступают автомобильные дороги, линии электропередачи, заводские территории и т. д.

При моделировании малых перемещений зданий обобщенные координаты qi рассчитывались по вектору приращений V03(∆x, ∆y) для третьего здания [7]. Методика определения направления вектора V03 изложена в работе [7]. Линейная система уравнений, определяющая взаимосвязь приращений обобщенных координат ∆qi и компонентов вектора V03(∆x, ∆y), задает р-плоскость размерности, равной четырем [13, 14]. Для обеспечения уменьшения значений обобщенных координат qi(i = 3, 4, …, 6) использовались отрицательные значения весовых коэффициентов приращений третьей и пятой обобщенных координат [7]. Высота зданий в тестовом примере была принята соответственно: Н1 = 50 м, Н2 = 150 м и Н3 = 100 м. При моделировании синтеза перемещений зданий в соответствии с архитектурными требованиями значения углов βi могут исследоваться только равными для заданных соответствующих сооружений.

Функции, заданные полиномами (3)–(4), могут быть использованы при автоматизированном определении места расположения зданий [7] с выполнением требований инсоляции. Результаты моделирования синтеза малых перемещений строящихся сооружений с целью размещения их с обеспечением максимального уровня освещенности и с использованием расчета узловых точек конвертов теней по разработанному способу показывают сокращение времени расчета. Использование способа определения теней и место расположения зданий с учетом минимизации занимаемой ими площади может быть применено при составлении планов территорий новой застройки различными жилыми сооружениями.

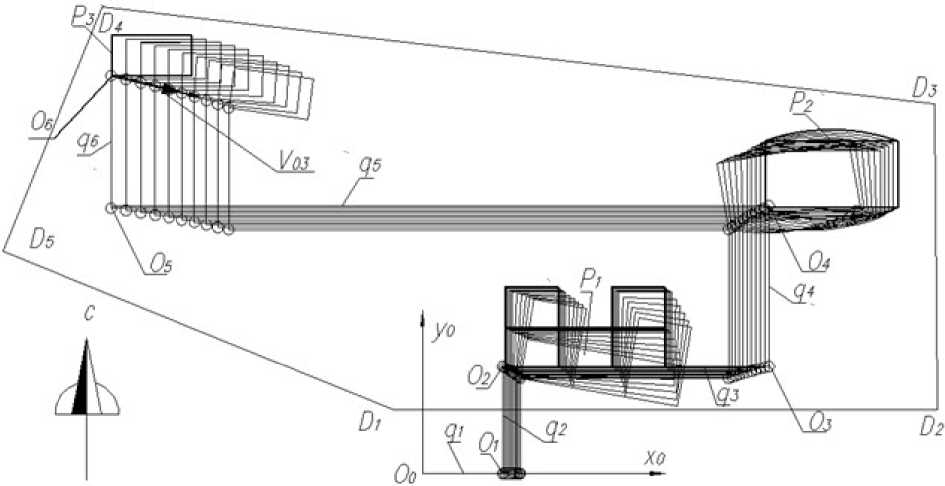
Рис. 5. Результаты моделирования движений зданий с выполнением требований инсоляций