Метод защиты векторных карт с использованием изображения ЦВЗ как вторичного контейнера

Основная идея большинства существующих методов активной (при помощи цифровых водяных знаков (ЦВЗ)) защиты векторных картографических данных заключается во встраивании ЦВЗ путём изменения координатной информации векторных объектов [1]. Данные методы, в зависимости от уровня стойкости встроенной информации к искажениям, направлены на решение различных задач безопасности векторных карт.

Методы [2–8] направлены на решение проблемы защиты авторских прав (защиты от несанкционированного распространения) с помощью стойких ЦВЗ. Методы защиты от изменений реализуются на основе полухрупких [9, 10] и хрупких [11] ЦВЗ, которые применяются для обеспечения соответственно подлинности и целостности векторных данных. Также одним из распространённых подходов к защите от изменений является технология zero-watermarking [12], которая подразумевает построение ЦВЗ на основе характеристик контейнера. При этом процедура встраивания как таковая отсутствует: ЦВЗ необходим только при процедуре верификации. Комбинированное применение различных технологий ЦВЗ носит название multiple watermarking [13] и позволяет обеспечить комплексную защиту векторных данных от изменений и несанкционированного распространения.

Существуют ситуации, когда даже незначительные изменения данных недопустимы. По этой причине возник ещё один класс методов защиты вектор- ных данных, reversible watermarking [14–16], обеспечивающий возможность восстановления значений координат после извлечения ЦВЗ. Однако эти методы не демонстрируют достаточной стойкости, следовательно, искажение карты может привести к невозможности корректного восстановления исходных координатных значений.

Все упомянутые выше методы имеют недостатки:

– Несмотря на то, что все преобразования выполняются с заданной точностью и практически не заметны для пользователя, любое искажение карты даёт злоумышленнику возможность детектировать наличие ЦВЗ различными методами стегоанализа.

– Набор объектов карты при встраивании и извлечении ЦВЗ должен быть строго упорядочен. Отсюда возникает необходимость хранения дополнительных меток идентификаторов объектов или позиций для встраивания.

Метод встраивания, предложенный нами ранее в [17], лишен вышеперечисленных недостатков. Во-первых, метод не предполагает изменения координат вершин: защитная информация вносится в картографические данные путём управляемого циклического сдвига списка вершин каждого полигона. Во-вторых, в качестве цифрового водяного знака рассматривается растровое изображение, геометрически совмещённое с картой, поэтому исчезает необходимость фиксировать порядок индексации объектов при встраивании и извлечении ЦВЗ.

Новый подход к защите векторных картографических данных, описанный в [17], может лечь в основу целой группы методов, ориентированных на конкретные задачи, такие как защита авторских прав, проверка подлинности и целостности картографических данных, а также локализация несанкционированных изменений.

В данной статье предлагается конкретный способ использования «шумоподобного» изображения в качестве вторичного контейнера для ЦВЗ, представленного в форме битовой последовательности, и исследуется вопрос информационной ёмкости такого контейнера.

Краткое описание базового метода встраивания ЦВЗ

Метод встраивания ЦВЗ в векторные картографические данные [17] основан на следующих свойствах полигональных объектов карты:

• а)    все полигоны являются замкнутыми объектами;

• б)    вершины каждого полигона пронумерованы последовательно.

Эти свойства обеспечивают возможность циклически сдвигать номера всех вершин полигона, не изменяя при этом значения координат вершин, то есть без каких-либо искажений векторной карты.

Таким образом, первая идея метода [17] заключается в том, что ЦВЗ встраивается в данные путём циклического сдвига списка вершин полигонов. Например, для встраивания в полигон одного бита ЦВЗ сдвиг можно осуществить таким образом, чтобы в зависимости от встраиваемого бита первой в списке оказалась либо самая верхняя (северная), либо самая нижняя (южная) вершина полигона. В общем случае можно рассматривать встраивание в полигон b -разрядного двоичного числа.

Вторая идея метода состоит в использовании некоторого растрового изображения, геометрически совмещённого с векторной картой и покрывающего достаточно большую её площадь. Полигональные объекты векторной карты будут геометрически совпадать с некоторыми пикселями изображения. Множество пикселей, значение каждого из которых закодировано в своём полигоне, соответствует множеству центров тяжести полигонов. Оно образует на плоскости нерегулярную сетку, по которой полное изображение может быть приближённо восстановлено каким-либо известным методом интерполяции [18].

Развитие базового метода

В методе [17] в качестве стойкого ЦВЗ, обеспечивающего защиту авторских прав на цифровую карту, использовалось само встраиваемое изображение. При этом аутентификация карты осуществлялась путём визуального сопоставления некоторого эталонного изображения с изображением, восстановленным (как правило, с большими погрешностями) из векторной карты. Это является очевидным недостатком метода, ограничивающим его применение.

Развивая базовый метод, мы предлагаем использовать «шумоподобное» изображение в качестве вто- ричного контейнера для ЦВЗ, представленного в форме битовой последовательности [19]. Это позволит автоматизировать процедуру аутентификации карты, поскольку битовая последовательность ЦВЗ может сама нести всю необходимую идентифицирующую информацию, для анализа которой не требуется сравнение с эталоном.

Чтобы обеспечить устойчивость битового ЦВЗ к погрешностям интерполяции, удалению или добавлению объектов, геометрическим трансформациям, обрезке карты и т.п., каждый бит, встраиваемый в изображение-контейнер, не должен быть привязан к отдельной точке (пикселю) или локальной области на плоскости изображения. Мы предлагаем встраивать битовую последовательность в пространственночастотную область изображения-контейнера так, чтобы каждый бит «голографически» занимал всю его плоскость, представлял собой двумерную синусоиду соответствующей пространственной частоты.

Формирование изображения ЦВЗ

Для простоты изложения будем пока считать изображение-контейнер непрерывным – f н ( t 1 , t 2 ). Пусть оно должно нести в себе произвольную бинарную последовательность ЦВЗ длиной L:

• 1,    1 <  l <  L . 0

  S = { 5 1 5 2 ... S l }, 5 1 =

  
  

Мы предлагаем формировать двумерный пространственный спектр изображения – F н (ω 1 , ω 2 ) – в виде 2( L+ 2) двумерных дельта-импульсов, расположенных в спектральной области на двух кольцах разных радиусов: r и r+ A r , то есть так, как проиллюстрировано на рис. 1 для одной полуплоскости двумерного спектра (в силу вещественности изображения на вторую полуплоскость спектр отображается центрально-симметрично). На этом рисунке дельта-импульсы условно обозначены черными кружками. Все импульсы, кроме двух, расположены с равным шагом по углу от начала координат спектра, в зависимости от значения соответствующего бита последовательности – на кольце меньшего или большего радиуса. Два импульса служат «ключом» начала последовательности, они размещаются на обоих кольцах при одинаковом (условно при-

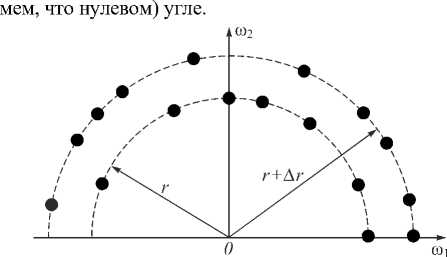
Рис. 1. Иллюстрация встраивания в спектр двоичной последовательности

На всей плоскости частотных аргументов полученный спектр изображения описывается формулой:

F , ( Op ® 2 ) =

L

= Z§(to1 -pl cos ф l, to2 -pl sin ф l) + l=1

+5 ( to 1 - r , to ₂) + 5 ( to 1 - r -A r , to ₂) +                  (1)

L

+^5(to1 + pl cos фl, to2 + pl sin фl) + i=1

+5(to1 + r, to2) + 5(to1 + r + Ar, to2), где

.             n l pI = r + Si Ar, фI =      ,

L + 1

5 ( ® 1 , to ₂) - двумерный дельта-импульс, обобщённая функция с известными свойствами [20]:

5 ( ® 1 , to ₂)

да ,

0,

при to 1 =to 2 = 0;

иначе.

да да

J J 5 ( ® 1 , ю ₂) W ( ® 1 , ® ₂)d ® 1 d ® ₂ = W (0,0),

-да -да для W(toi,to2) - произвольной непрерывной функции.

Через двумерное обратное преобразование Фурье от спектра (1) можно перейти к самой двумерной функции изображения:

f, (t1, t2) = да да

= "2 J J F_H ( ® 1 , ® 2 ) е ' 1    t ²⁾ d ® 1 d ® ₂.

^{4 П} -да-да

Подставив (1) в (2), с учётом формулы Эйлера получаем:

1 f L^

L ⁽ t 1 , t 2 ) = ₂ 2 i Z ^cos[( p l cos ф l ) t 1 ⁺

^{2 n} L i = 1                                          (3)

+ ( p l sin ф l ) 1 ₂ ] + cos ( rt 1 ) + cos[( r + A r ) 1 ₂ ] } .

Приведённые соотношения описывают лишь принцип встраивания бинарной последовательности ЦВЗ в изображение-контейнер. На практике при работе с цифровым изображением вместо непрерывного спектра необходимо использовать дискретное преобразование Фурье (ДПФ), принимая во внимание известные особенности такого перехода: целочисленность аргументов в пространственной и спектральной области, двумерную периодичность функций, возможные эффекты наложения и т.д. [20]. При этом, чтобы сформировать «шумоподобное» изображение, несущее ЦВЗ, размером N 1 × N 2 пикселей, имеются две возможности:

• 1)    Можно напрямую использовать «дискретизированный» аналог формулы (3):

  L

  f ( П 1 , n 2 ) = Z cos

  l = 1

  
  

r ^p l cos ф l     ^p l sin ф l

П                      n- 1

I   N1     1     N22

Г 2 n r )     Г 2 n ( r + A r )

+ cos n + cos n,

I N1 1J      I    N22

где n 1 – целочисленные аргументы цифрового изображения, 0 <  n 1 <  N 1 - 1, 0 < n ₂ <  N 2 -1.

• 2)    В двумерной дискретной спектральной области расставить единичные импульсы [20] (вместо дельтаимпульсов) на двух кольцах так, как было описано выше, а затем – при помощи обратного ДПФ – получить само изображение.

При малых длинах L последовательностей вычислительно эффективнее может оказаться первый способ, при больших – второй.

Заметим, что в силу дискретности спектра координаты единичных импульсов, т.е. величины p l cos ф l , p l sin ф l , r , ( r + A r ) должны быть округлены до целочисленных значений и, следовательно, могут неточно попадать на кольца. Чтобы эти погрешности были незаметны (не влияли на дальнейшее извлечение ЦВЗ), размеры ДПФ и радиусы окружностей r , ( r + A r ) должны быть достаточно большими.

На последнем шаге формирования изображения с ЦВЗ его пиксели могут быть приведены к стандартному диапазону значений, например, [0, 255]:

f 255 ( n 1 , n 2 ) = 255

f ⁽ n 1 , n 2 ) - min f ⁽ n 1 , n 2 ) n ₁, n ₂

max f ( n 1 , n ₂) - min f ( n 1 , n ₂) n ₁, n ₂                          n ₁, n ₂

Пример результирующего «шумоподобного» изображения с ЦВЗ, соответствующим рис. 1, представлен на рис. 2.

Рис. 2. Пример изображения с ЦВЗ (N 1 =N 2 =512, r=8, ∆r=4, L=15, B ={101101001011101} )

Извлечение ЦВЗ из изображения

Процедура извлечения ЦВЗ из изображения, приближённо (с интерполяцией) восстановленного из векторной карты, состоит из следующих очевидных шагов:

• 1)    вычисление двумерного дискретного спектра (выполнение обратного ДПФ) изображения;

• 2)    выявление и определение координат спектральных компонент, имеющих большую амплитуду (импульсов);

• 3)    проверка наличия ЦВЗ, т.е. факта расположения импульсов на двух концентрических кольцах в спектральной плоскости; оценка радиусов этих колец;

• 4)    нахождение на кольцах ключа начала последовательности, т.е. пары импульсов, располо-

• женных под одинаковым углом к началу координат двумерного спектра;

• 5)    собственно считывание бинарной последовательности ЦВЗ – в направлении по часовой или против часовой стрелки от ключа.

Предлагаемый нами способ формирования ЦВЗ (в виде импульсов на окружностях в спектральной плоскости), вместе с процедурой его извлечения, описанной выше, обеспечивают устойчивость ЦВЗ к основным геометрическим деформациям изображения и, соответственно, векторной карты, в которую оно встроено: масштабированию, повороту, сдвигу, кадрированию (вырезанию фрагмента).

Экспериментальные исследования

Для исследования потенциальных возможностей использования «шумоподобного» изображения, встраиваемого в векторную карту, в качестве вторичного контейнера для ЦВЗ, представленного в форме битовой последовательности, были проведены вычислительные эксперименты.

Во всех экспериментах генерировались цифровые изображения размерами N 1 × N 2 = 512×512 пикселей. Битовые ЦВЗ встраивались в кольца радиусов r и ( r + Δ r ) в области дискретного спектра изображения. Для определённости было выбрано Δ r =4: минимальное расстояние между кольцами, необходимое для надёжного извлечения встроенной битовой последовательности ЦВЗ, установленное эксперименталь ным путём. Рассматривались «н изкоча стотные» ( r = 10, 50 ) и «среднечастотные» ( r = 60,100) «шумоподобные» изображения.

Длины битовых последовательностей ЦВЗ варьировались в диапазоне 10 ≤ L ≤ 100. Значения символов последовательностей генерировались при помощи датчика случайных чисел как равновероятные и независимые, по 100 реализаций ЦВЗ для каждого сочетания параметров.

Интерполяция изображения, извлечённого из векторной карты в виде нерегулярной сетки пикселей, осуществлялась методом ближайшего соседа на основе триангулированной нерегулярной сети [18] .

Для нахождения больших спектральных импульсов использовалось простое правило:

m _k a _k x I F ( k ₁, k ₂), ( k ₁, k ₂) ≠ (0,0)

F ( k 1 , k 2 ) >  ¹ ₂

где F ( k 1 , k 2 ) – ДПФ изображения, k 1 , k 2 – целочисленные аргументы дискретного спектра (0 ≤ k 1 ≤ N 1 – 1, 0 ≤ k 2 ≤ N 2 – 1).

Эксперимент 1

Основными источниками погрешностей восстановления изображения-контейнера из векторной карты и, соответственно, ошибок извлечения битовой последовательности ЦВЗ, очевидно, являются:

– сильное прореживание изображения при его встраивании в карту: оно сохраняется в виде набора разрозненных пикселей, соответству- ющих центрам тяжести полигональных объектов карты;

– огрубление (квантование) сохранённых пикселей из-за того, что в каждый полигон возможно встраивание лишь одного или нескольких двоичных разрядов.

Для количественной оценки влияния этих искажений на ЦВЗ был проведён следующий вычислительный эксперимент. В сформированном изображении ЦВЗ случайным образом (независимо и равновероятно по каждой координате) выбиралось K пикселей, каждый из которых огрублялся до b -разрядного двоичного числа (квантовался на 2 ^b уровней). Далее производилась интерполяция изображения, попытка извлечения битовой последовательности ЦВЗ и оценка вероятности правильного извлечения.

В качества показателя целостности ЦВЗ рассматривалась экспериментально оцениваемая вероятность правильного извлечения двоичной последовательности – P в зависимости от числа опорных пикселей K. В качестве варьируемых величин были взяты радиус r , разрядность b и длина последовательности L.

Минимальные значения радиусов, при которых надёжно обеспечивается работоспособность предлагаемого способа встраивания, установлены опытным путём и могут быть приближённо описаны формулой:

r ≥ 0,36 L .                                       (4)

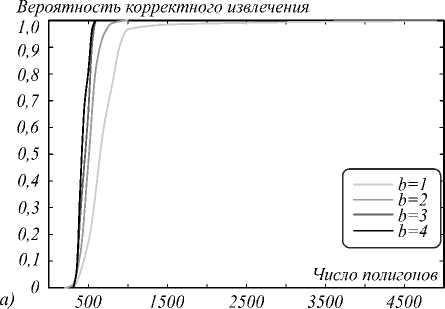
На рис. 3 представлена зависимость вероятности правильного извлечения от числа полигонов при варьируемых значениях разрядности для следующих случаев: а) L = 10, б) L =50, в) L = 100 (радиусам в каждом случае присвоены минимально возможные значения).

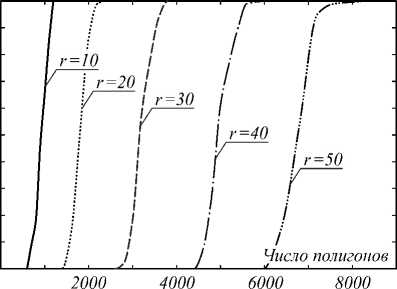
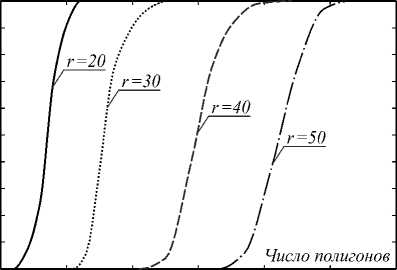
На рис. 4 представлена зависимость вероятности правильного извлечения от числа полигонов при варьируемых значениях радиусов для следующих случаев: а) L = 10, б) L = 50, в) L = 100 (значение разрядности в данном случае фиксировано: b = 3).

Из представленных результатов можно сделать несколько достаточно очевидных выводов.

Чем больше объектов на карте (пикселей, соответствующих полигонам), тем, естественно, с более высокой вероятностью осуществляется правильное извлечение ЦВЗ. В то же время, чем длиннее битовая последовательность ЦВЗ, тем выше требования к числу объектов, необходимому для ее извлечения.

Качество извлечения ЦВЗ повышается с ростом разрядности двоичных слов – пикселей, соответствующих объектам карты. Это также выглядит естественным, поскольку увеличение разрядности уменьшает шум квантования пикселей и, соответственно, погрешность восстановления изображения-контейнера. Однако увеличение разрядности выше b =3 почти не дает эффекта повышения качества. Более того, в практических приложениях оно трудно осуществимо из-за того, что обычно на карте доминируют простые полигоны – четырехугольники, в которые удается встраивать не более, чем трехразрядные двоичные числа: два разряда – задавая начало обхода с одной из вершин четырехугольника, третий разряд – меняя направление обхода.

Вероятность корректного извлечения 1,0 0,9 0,8 0.7 0,6 0,5 0,4 0,3 0,2 0.1

• а) О

  
  
  

Вероятность корректного извлечения 1.0 0,9 0,8 0,7 0,6 0,5 0,4 0.3 0.2 0.1

О

Вероятность корректного извлечения 1,0 0,9 0,8 0,7 0.6 0,5 0,4 0,3 0,2 0.1

О

б)  2000 4000   6000   8000 10000 12000

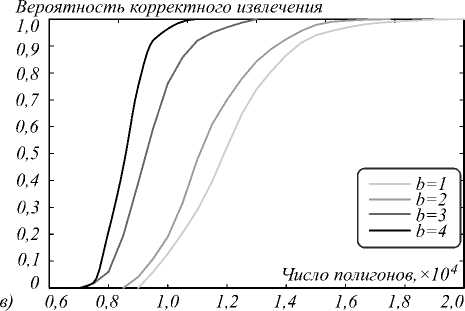
Рис. 3. Зависимость вероятности правильного извлечения

от числа полигонов при варьируемых значениях разрядности L=10, r=4 (а); L=50, r=18 (б); L=100, r=36 (в)

При фиксированной длине встраиваемой битовой последовательности качество извлечения ЦВЗ тем выше, чем меньше r , т.е. чем более низкочастотным является изображение-контейнер. С другой стороны, минимально возможное значение этого параметра лимитировано дискретностью двумерного спектра изображения, в «кольцо» которого встраивается последовательность длиной L , см.формулу (4).

На рис. 5 представлена зависимость параметра емкости b × L от числа полигонов при варьируемых значениях длины последовательности и фиксированном значении достижимой вероятности правильного извлечения двоичной последовательности .

б)  2000 4000   6000   8000 10000 12000

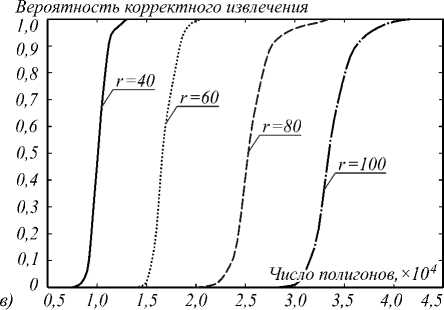
Рис. 4. Зависимость вероятности правильного извлечения от числа полигонов при варьируемых значениях радиусов а) L =10, b=3; б) L =50, b=3; в) L =100, b=3

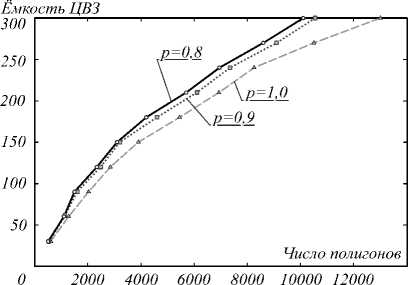
Рис. 5. Зависимость емкости контейнера от числа полигонов при варьируемых значениях длины последовательности p=1 (а); p=0,9 (б); p=0,8 (в)

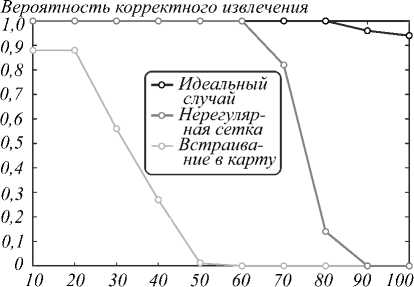
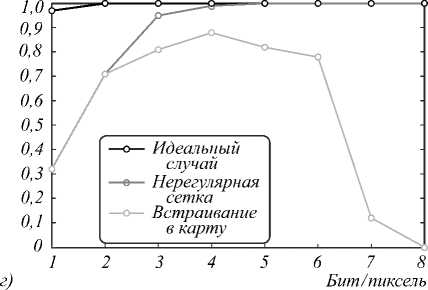
Эксперимент 2

В предыдущем эксперименте встраивание изоб- ражения в карту имитировалось, но реально не осуществлялось. Для подтверждения работоспособности предлагаемого способа внесения ЦВЗ в векторные картографические данные был использован фрагмент плана городской застройки, содержащий 9 327 полигонов (рис. 6). Рассматривались варианты внесения в каждый полигон карты квантованных значений соответствующих пикселей с последую- щим извлечением.

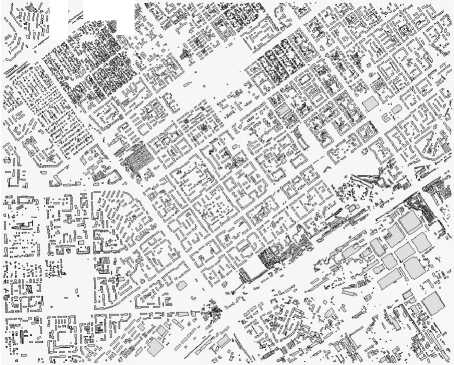
Рис. 6. Карта-контейнер

Помимо подтверждения работоспособности метода на реальных данных, этот эксперимент направлен на качественную оценку влияния погрешностей, вносимых такими данными, относительно идеального (модельного) случая, представленного в предыдущем эксперименте.

Ранее при моделировании погрешностей метода интерполяция производилась по равномерно разбросанным точкам, а квантование пикселей производилось строго по заданному уровню. В эксперименте 2 мы будем исследовать вероятности корректного извлечения последовательности ЦВЗ из трёх «шумоподобных» изображений, то есть рассмотрим три различных случая, демонстрирующие влияние погрешностей метода встраивания:

• 1)    Идеальный случай (аналогичен модели из эксперимента 1). Интерполяция производится по маске с равномерно разбросанными 9327 точками (рис. 7 а ), наложенной на квантованные по заданному уровню «шумоподобные» изображения.

• 2)    Интерполяция производится по нерегулярной сетке извлеченных из карты 9327 пикселей (рис. 7 б ), наложенной на квантованные по заданному уровню «шумоподобные» изображения. Эти данные позволят нам проследить, как неравномерность сетки влияет на результат интерполяции и результат извлечения ЦВЗ в целом.

• 3)    Реальное встраивание ЦВЗ и его извлечение из карты. Эти данные позволят нам проследить, как влияет разброс числа вершин полигонов на результат извлечения.

Для вычисления вероятностей корректного извлечения эксперимент проводился на выб орках случайных ЦВЗ размера 100 для L = 10,100 (радиусы спектральных колец выбраны минимальными).

а)

б)

Рис. 7. Пример равномерной (а) и неравномерной (б) сетки для интерполяции

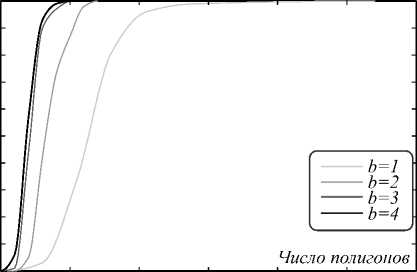
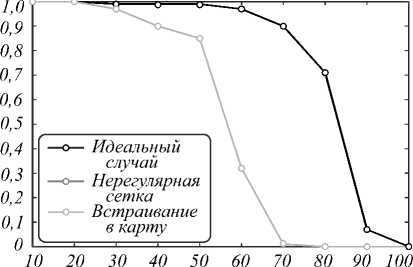
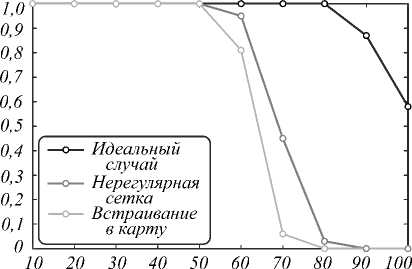
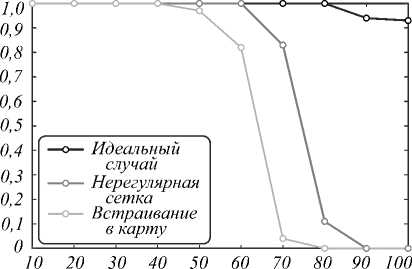
Зависимости вероятности ошибок извлечения от длины битовой последовательности ЦВЗ при варьируемых значениях b приведены на рис. 8.

Для b = 1,2 результаты извлечения из карты совпадают с ошибками интерполяции по нерегулярной сетке. Для b >  3 извлечение из реальных данных начинает сопровождаться ошибками, вызываемыми разбросом числа вершин полигонов.

Зависимости вероятности ошибок извлечения от количества уровней квантования изображения ЦВЗ при варьируемых значениях длины встраиваемой битовой последовательности приведены на рис. 9.

Выводы эксперимента 1 говорят о том, что качество извлечения ЦВЗ тем выше, чем больше b. На реальных данных это выполняется только для b = 1,4 . Чем больше L, тем сильнее падение качества при b > 4. При b = 8 извлечение не представляется возможным для любых L. Этот эффект обусловлен сильным разбросом числа вершин в полигонах. На рис. 10

приведена статистика по числу вершин полигонов для исследуемой в эксперименте карты.

Вероятность корректного извлечения

а)                Длина последовательности ЦВЗ

Вероятность корректного извлечения

б)                Длина последовательности ЦВЗ

Вероятность корректного извлечения

в)                Длина последовательности ЦВЗ

Длина последовательности ЦВЗ

Рис. 8. Зависимости вероятности ошибок извлечения от длины битовой последовательности ЦВЗ для b=1 (а); b=3 (б); b=5 (в); b=8 (г)

г)

Для встраивания b -битного числа в полигон без погрешностей данный полигон должен иметь не менее 2^b - вершин. Например, для встраивания числа из 3 бит полигон должен иметь 4 вершины: такие полигоны являются наиболее вероятными для карт застройки. Для встраивания 5 бит необходимо уже 16 вершин, что маловероятно для данного типа карт.

Заключение

В данной статье приведено исследование метода встраивания ЦВЗ в векторные картографические данные на основе циклического сдвига списка вершин полигональных объектов.

Предложена модификация метода, позволяющая автоматизировать процедуру аутентификации, а также повысить стойкость метода к изменению содержимого карты. Основная идея улучшенного метода заключается в использовании «шумоподобного» изображения в качестве вторичного контейнера для ЦВЗ, представленного в форме битовой последовательности. Предложен алгоритм формирования изображения-контейнера для заданной последовательности ЦВЗ, а также алгоритм извлечения такой последовательности.

Проведено экспериментальное исследование информационной емкости изображения-контейнера и его стойкости к искажениям, моделирующим встраивание в реальные картографические данные: квантованию и добавлению шума, обусловленного интерполяцией изображения по случайным пикселям.

Проведена проверка работоспособности метода на реальных картографических данных, в целом подтвердившая результаты моделирования.

Сформированы выводы по рациональному выбору параметров для надежного извлечения встроенной битовой последовательности ЦВЗ в зависимости от числа полигонов векторной карты.

Дальнейшие исследования планируется вести в следующих направлениях:

• 1)    более полное исследование методов интерполяции изображений, заданных нерегулярной сеткой пикселей, применительно к решаемой задаче;

• 2)    анализ устойчивости ЦВЗ к геометрическим преобразованиям и к изменению содержания векторной карты, таким как добавле-ние/удаление вершин/объектов/слоёв;

• 3)    разработка методов повышения устойчивости ЦВЗ к конкретным видам атак на векторные картографические данные.

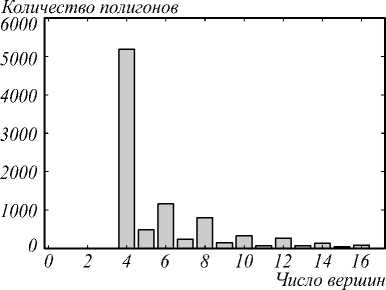
Рис. 10. Распределение количества вершин для фрагмента городской застройки

a)

Вероятность корректного извлечения 1,00

0,98

0,96

0,94

0,92

0,90

0,88

Идеальный случай

Нерегулярная сетка

Встраивание в карту

Бит/пиксель

0,98

0,96

0,94

0,92

0,90

0,88

б)

Вероятность корректного извлечения 1,00

—о— Идеальный случай

—о- Нерегулярная сетка

—о- Встраивание                      _ в карту

Бит/пиксель

Вероятность корректного извлечения 1,0 0,9 0,8 0,7

0,6 ■ 0,5 ■ 0,4 ■ 0,3 ■ 0,2 ■ 0,1 -

О L

Идеальный случай

Нерегулярная сетка

Встраивание в карту

Бит/пиксель

Вероятность корректного извлечения

Вероятность корректного извлечения                 Вероятность корректного извлечения

в)

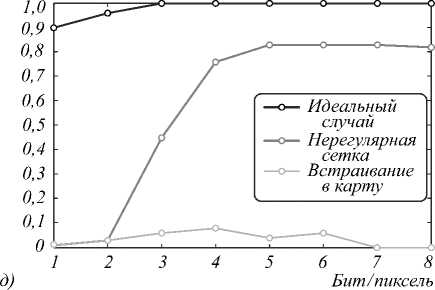
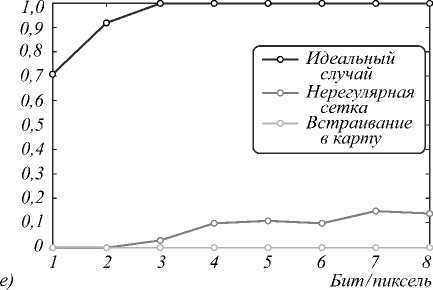
Рис. 9. Зависимости вероятности ошибок извлечения от количества уровней квантования

для L=10 (а); L=30 (б); L=50 (в); L=60 (г); L=70 (д); L=80 (е)

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант

№ 19-07-00474 А) и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26).