Методическая помощь бизнес-аналитику в изучении особенностей решения оптимизационных задач при имитационном моделировании

Существует четкое различие между оптимизацией на основе обычных математических моделей и оптимизацией с использованием имитационных моделей.

В обычной математической модели задача оптимизации выражается с помощью явных математических функций, зависящих от управляемых переменных. В подобных моделях после постановки оптимизационной задачи и её решения находятся искомые значения управляемых переменных, соответствующие экстремуму целевой функции модели [1, с. 10].

Имитационная модель строится вне рамок оптимизационного процесса. Т.е. процедура построения самой имитационной модели не имеет никакого отношения к постановке и решению оптимизационной задачи. Готовую имитационную модель, как правило, используют для получения оценочных характеристик показателей функционирования системы при заданных значениях управляемых переменных. Это означает, что в имитационных моделях значения управляемых переменных (если их рассматривать вне процедуры оптимизации) считаются как часть входных данных [2, с. 354].

При решении оптимизационной задачи с применением имитационного моделирования, на самом деле, осуществляется постановка статистического эксперимента. Попробуем изложить методику данного процесса.

Необходимые результаты моделирования получаются путем целенаправленного изменения значений управляемых переменных. Но, дело в особенностях процедуры: при одних и тех же значениях управляемых переменных реализуются многократные прогоны имитационной модели для получения совокупности данных, элементы которых представляют собой текущие значения выходных показателей. На основе множества данных вычисляются оценочные характеристики результативных показателей (их средние значения и среднеквадратические отклонения). Далее осуществляется переход к следующим значениям управляемых переменных и процедура повторяется.

Полученные оценочные характеристики и используются для выполнения оптимизационных процедур. Следует помнить, что в имитационном моделировании для сравнения усредненных оценок, которые получены при любых комбинациях управляемых переменных, должны использоваться соответствующие статистические тесты [2, с. 355].

Процесс оптимизации с применением имитационных моделей усложняется из-за присутствия выборочной ошибки. Например, разброс оценок результатов моделирования может быть связан выборочной ошибкой, а не изменением значений управляемых переменных. Невозможность различить эти две причины разброса выходных данных затрудняет сравнение результатов моделирования при различных комбинациях управляемых переменных.

Полностью избавиться от выборочной ошибки нельзя, но ее влияние можно уменьшить путем увеличения количества прогонов имитационной модели. Доказано, что при выполнении N прогонов имитационной модели для каждой комбинации значений управляемых переменных выборочная ошибка уменьшается в 1 / VV раз [2, с. 355].

Чтобы объяснить специфику решения оптимизационной задачи с использованием имитационной модели, рассмотрим задачу управления запасами, в которой спрос на продукцию имеет вероятностную природу.

Выяснили, что известные методики построения и эксплуатации математических моделей задач управления запасами адресованы для обучающихся и специалистов с повышенной математической подготовкой [3, с. 184]. Мы сформулировали упрощенную версию модели задачи управления запасами, чтобы уделить максимум внимания на процедуры оптимизации вероятностной системы с применением имитационного моделирования. Надеемся, что подобный подход поможет бизнес-аналитикам с базовым прикладным обра- зованием разобраться в сути методологии решения оптимизационных задач при имитационном моделировании.

Специфика задачи управления запасами .

• -    Текущий спрос на продукцию заранее не известен.

• -    Когда количество произведенной продукции превысит спрос, то образуется запас (излишки) с затратами на хранение.

• -    Когда текущий спрос превышает количество произведенной продукции, то будут издержки из-за дефицита, поскольку будут штрафные санкции за не поставленную продукцию.

Целью моделирования системы управления запасами является определение оптимального значения объема производства продукции, которое минимизирует суммарные затраты, связанные с функционированием системы. Суммарные затраты определяются как сумма двух видов показателей:

• а)    затрат на хранения запасов (излишек);

• б)    затрат из-за нехватки запасов (из-за дефицита готовой продукции).

Для проектирования модели системы управления запасами нами заимствованы исходные данные задачи, которая приведена в электронном ресурсе [4].

Постановка задачи .

Предприятие занимается производством определенного вида штучной продукции. Сначала необходимо построить имитационную модель функционирования предприятия в течение определенного времени, называемого продолжительностью периода моделирования. В нашем случае, упомянутый параметр равен 15-и месяцам.

Исходные данные:

• а)    затраты на хранение единицы продукции – 60$;

• б)    затраты для покрытия дефицита единицы продукции – 160 $ ;

• в)    начальный уровень запаса продукции – 5 штук;

• г)    объем производства продукции за месяц – 40 штук.

Спрос на продукцию является случайной величиной с нормальным распределением: со средним значением – 40 штук за месяц и со среднеквадратическим отклонением – 5 штук за месяц.

Алгоритм расчета .

Остаток на складе по истечении первого месяца равен:

• а)    начальному уровню запаса продукции плюс объему производства продукции за месяц с вычетом текущего спроса (когда текущий спрос меньше суммы начального уровня запаса и объема производства за месяц);

• б)    нулю, в других случаях.

Остаток на складе по истечении любого месяца (кроме первого) равен:

• а)    объему производства продукции за месяц плюс остаток от предыдущего месяца с вычетом текущего спроса (когда текущий спрос меньше суммы объема производства и остатка от предыдущего месяца);

• б)    нулю, в других случаях.

Суммарные затраты рассчитываются в зависимости от наличия остатка , либо неудовлетворенного спроса .

Первичные расчеты выполнялись на табличном процессоре MS Excel. Фактический спрос на продукцию смоделирован с применением программы табличного процессора для генерирования случайных чисел с нормальным законом распределения. Т.е., данные по ежемесячному спросу на продукцию предварительно сгенерированы и занесены в электронную таблицу. Запас продукции и суммарные затраты вычислены с использованием изложенного выше алгоритма.

В таблице 1 приведены итоговые результаты моделирования. К сведению: полученные результаты соответствуют только для конкретной реализации данных по спросу на продукцию. Для других реализаций данных по спросу результаты по запасу продукции и суммарным затратам будут иные.

Таблица 1

Моделируемые месяцы	Спрос на продукцию, шт.	Запас продукции, шт.	Суммарные затраты, $
1	27	18	1080
2	40	18	1080
3	37	21	1260
4	48	13	780
5	50	3	180
6	42	1	60
7	41	0	0
8	37	3	180
9	43	0	0
10	35	5	300
11	47	0	320
12	27	13	780
13	37	16	960
14	32	24	1440
15	38	26	1560

Итоговые результаты за период моделирования .

Общие затраты, $9980

Средние затраты, $665

Минимальные затраты, $0

Максимальные затраты, $1560

Средний объем запаса, шт.11

Минимальный объем запаса, шт.0

Максимальный объем запаса, шт. 26

Для выполнения многократных прогонов имитационной модели у табличного процессора MS Excel нет возможности. Поэтому, далее полностью переходим к С++ программам, разработанные и апробированные нами на базе платформы Visual Studio 2022.

Вводим понятие «прогон имитационной модели». Под этим понятием мы воспринимаем имитацию функционирования предприятия в течение продолжительности периода моделирования, равное 15-и месяцам.

В таблице 2 приведены результаты одного прогона имитационной модели при различных значениях объема производства продукции. В данном эксперименте использована та же реализация значений спроса на продукцию, которая использована в таблице 1. На рисунке отображено графическое представление данных таблицы 2.

Таблица 2

Объем производства продукции, шт	Общие затраты, $
20	44160
25	32340
30	20820
35	12480
40	9980
45	45060
50	81060
55	117060
60	153060
65	189060
70	225060
75	261060
80	297060

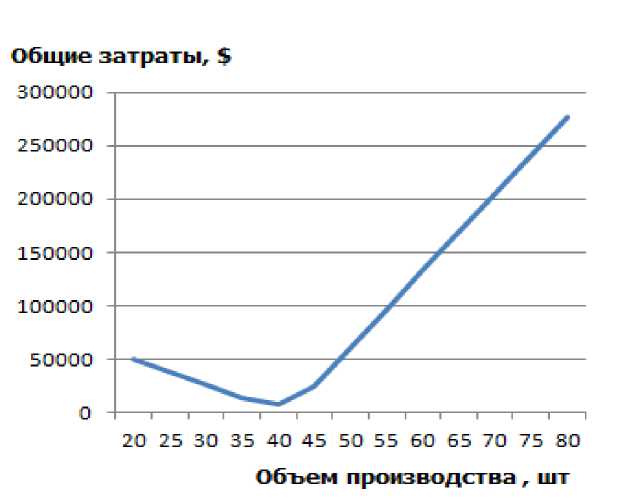
Рисунок. Графическое представление данных таблицы 2.

В таблице 3 приведены результаты (средние значения суммарных затрат и их среднеквадратические отклонения) ста прогонов имитационной модели при значениях объема производства продукции из интервала от 20 до 80 штук с шагом изме- нения 5 штук. Подчеркиваем, что для каждого прогона имитационной модели была использована сгенерированная по специальному алгоритму оригинальная реализация значений спроса на продукцию за период моделирования.

Таблица 3

Объем производства продукции, шт	Суммарные затраты, $
	среднее значение	среднеквадратическое отклонение (СКО)
20	48525	3531
25	35798	3071
30	24444	3338
35	13251	2751
40	8938	3761
45	36536	10333
50	74372	10322
55	107855	10479
60	145142	11889
65	181466	10322
70	215311	9929
75	251747	10789
80	286859	10338

В левой части таблицы 4 приведены результаты другого ста прогонов имитационной модели при значениях объема производства продукции из интервала от 20 до 80 штук с шагом изменения 5 штук (как и в таблице 3).

Различные значения статистических характеристик (средних значений и средне- квадратических отклонений) суммарных затрат в таблицах 3 и 4 являются наглядным подтверждением того, что в имитационном моделировании при повторных экспериментах невозможно получить одинаковые результаты (в нашем случае, из-за вероятностной природы спроса на продукцию).

Таблица 4

Объем производства продукции, шт	Суммарные затраты, $		Нижняя граница доверительного интервала	Среднее значение суммарных затрат, $	Верхняя граница доверительного интервала
	среднее значение	СКО
20	48249	3326	47699	48249	48799
25	36420	2628	35986	36420	36854
30	24131	2900	23652	24131	24610
35	12312	2506	11898	12312	12726
40	8055	3613	7458	8055	8652
45	36923	9637	35330	36923	38516
50	72060	10504	70323	72060	73797
55	109527	10730	107753	109527	111301
60	144670	10387	142953	144670	146387
65	180841	9187	179322	180841	182360
70	217052	10198	215366	217052	218738
75	252707	9885	251073	252707	254341
80	288907	10657	287145	288907	290669

Важно, чтобы результаты имитационного моделирования были выражены в виде доверительных интервалов, которые показывают величину отклонения фактического результата моделирования от точного значения. Дело в том, что полученные результаты моделирования являются только точечными (оценочными) значениями. Подобные результаты с достаточным основанием можно было бы использовать только при очень больших объемах наблюдений (в нашем случае, при большом количестве моделируемых месяцев функционирования предприятия).

Чем меньше объем выборки, тем меньше доверия к результатам. В таком случае важно не только получить требуемое точечное значение показателя, но и определить, насколько эта оценка близка к истинному значению параметра, т.е. важно оценить величину ошибки с помощью доверительных интервалов.

Таким образом, необходима не только точечная, но и интервальная оценка параметров [5, с. 137]. Под интервальной оценкой понимается определение доверительного интервала значений, в котором с заданной вероятностью будет находиться искомый параметр. Доверительный интервал характеризуется нижней и верхней границами.

В правой части таблицы 4 приведены нижняя и верхняя границы доверительного интервала среднего значения суммарных затрат, вычисленные при значениях доверительной вероятности 95% и уровне значимости 5%.

Интервальная оценка результатов имитационного моделирования показывает, что минимальное среднее значение суммарных затрат – 8055$ из диапазона 7458$…8652$ обеспечивается при ежеме- сячном объеме производства продукции 40 штук. Важный вывод: нижняя и верхняя границы выявленного диапазона минимального среднего значения не пересекаются с соседними подобными граничными значениями.

Для повышения доверия к полученным результатам необходимо повторно промоделировать функционирование системы, но с другими параметрами:

• а)    выбрать более узкий интервал значений объема производства продукции, охватывающий текущее оптимальное значение 40 штук;

• б)    шаг изменения объема производства продукции должен равняться возможному минимальному значению.

В таблице 5 приведены результаты ста прогонов имитационной модели при каждом значении объема производства продукции из интервала от 35 штук до 45 штук с единичным шагом изменения.

Таблица 5

Объем производства продукции, шт.	Суммарные затраты, $		Нижняя граница доверительного интервала	Средние значения суммарных затрат, $	Верхняя граница доверительного интервала
	среднее значение	СКО
35	12801	2800
36	11075	2309
37	9207	2368	8816	9207	9598
38	8243	2826	7776	8243	8710
39	7922	3578	7330	7922	8514
40	8731	4078	8057	8731	9405
41	13068	7004
42	17655	8286
43	23572	9273
44	30319	8331
45	37023	11532

Интервальная оценка результатов имитационного моделирования показывает, что минимальное среднее значение суммарных затрат – 7922$ из диапазона 7330$…8514$ обеспечивается при ежемесячном объеме производства продукции 39 штук. Нижняя и верхняя границы диапазона минимального среднего значения суммарных затрат пересекаются с границами доверительных интервалов соседних минимальных средних значений (7776$...8710$ и 8057$...9405$). Вывод: между средними значениями суммарных затрат, которые соответствуют объемам производства продукции за месяц 38, 39 и 40 штук, статистически значимых различий нет (при доверительной вероятности 95% и уровне значимости 5%).

Выводы. Применение имитационного моделирования для решения оптимизационных задач усложняется спецификой использования имитационных моделей, поскольку результаты использования подобных моделей: а) подвержены статистическим ошибкам; б) должны интерпретироваться только с помощью соответствующих статистических тестов. Изложенные особенности имитационного моделирования создают трудности для получения независимых и устойчивых наблюдений. Можно сделать вывод, что в общем случае оптимизация с помощью имитационного моделирования не являет ся особо надежным методом исследова ния.