Методические аспекты использования данных биологического мониторинга по фитопланктону для биоиндикации качества вод в бассейне Волги

Московский государственный университет им. М.В. Ломоносова, г. Москва

Исследована возможность использования для целей биоиндикации количественных характеристик видового разнообразия фитопланктона, полученных по данным государственного экологического мониторинга пресных вод России. Использованы ретроспективные материалы по бассейну Волги. Проведен анализ влияния на характеристики разнообразия: 1) погрешностей в подсчете численностей клеток фитопланктона; 2) метода оценки параметров ранговых распределений; 3) степени адекватности формальной модели распределения; 4) зависимости между характеристикой выравненности разнообразия и видовым богатством; 5) сезона отбора проб; 6) принадлежности проб к тому или иному подбассейну или типу водного объекта; 7) прозрачности и температуры воды. Предложены характеристики разнообразия, адекватные имеющимся данным мониторинга. Произведена оценка границы между благополучными и неблагополучными значениями этих характеристик. Сформулированы рекомендации по применению характеристик разнообразия фитопланктона Волги для целей биоиндикации качества вод.

Задача биоиндикации экологического состояния природных объектов сводится к обоснованию расчетов по биологическим показателям критерия состояния на шкале «норма-нарушение» («благополучие-неблагополучие»). Предлагаемая читателю работа ориентирована на методические вопросы, касающиеся возможности использования для целей биоиндикации количественных характеристик видового разнообразия фитопланктона, полученных по многолетним данным экологического государственного мониторинга пресных вод России.

В этой системе в качестве инструмента биоиндикации принят классификатор Роскомгидро-мета [14], согласно которому оценка состояния по фитопланктону проводится с помощью индекса сапробности по Пантле и Буку в модификации Сладечека [24, 25]. При всей успешности такого подхода постоянно возникают разночтения относительно степени сапробности того или иного организма. Так, над расширением и уточнением списков видов-индикаторов, предложенных Р. Колквитцем и М. Марссоном, позднее работали многие исследователи. Далеко не все попытки расширения списков сапробности были одинаково удачными, некоторые из них вносили путаницу в систему биоиндикации [17]. Не всегда полученные по индексам сапробности оценки состояния экосистемы соответствуют реальной картине загрязнения водоема. Например, анализ многолетних рядов структурно-функциональных характеристик составляющих биоты Красноярского водохранилища в пространственном аспекте, с учетом степени антропогенного загрязнения вод, позволил выявить слабые стороны в информативности таких дескрипторов качества воды, как индекс сапробности, олигохетный и биотический индексы ( science). Hо основная претензия к индексам сап-робности состоит в том, что они по своему определению регистрируют лишь органические загрязнения вод и только косвенно могут указывать на загрязнения другой природы.

Один из альтернативных подходов к биоиндикации использует идеи о связи биологического разнообразия с качеством среды обитания живых организмов и об измерении разнообразия с помощью параметров распределений численности или биомассы организмов в сообществах [2, 3, 6, 12].

Обнаружено [6], что в нормальном (ненарушенном, фоновом и т.п.) состоянии сообщества параметр рангового распределения заключен во вполне определенном диапазоне значений. Пара- метр распределения специфичен для типа сооб-щества (например, для сообществ фитопланкто-на, зоопланктона или перифитона), для конкрет-ной экосистемы, для сложившегося комплекса условий среды, к которым адаптировано сооб-щество. В той степени, в какой справедлив ука-занный закон, отклонения от него могут служить мерой нарушенное™ состояний сообщества. Другими словами, предлагается «градусник» для экосистем, где роль температуры играет пара-метр рангового распределения.

Укоренившаяся в экологии практика индика-ции состояния экосистем по индексам их разно-образия оправдана тем, что все индексы разно-образия однозначно связаны с параметрами ран-говых распределений [6], а сами параметры мо-гут быть интерпретированы как первичные ин-дексы экологического разнообразия.

Следует уточнить, что отклонения ранговых распределений от нормы регистрируют стрессо-вые воздействия на сообщества. При длитель-ном сохранении нарушающего воздействия мо-жет произойти существенная перестройка струк-туры сообщества, замена входящих в него ви-ДОВ , но в результате адаптации параметры ран-гового распределения новых численностей новых групп организмов окажутся в пределах нормы.

Ранговые распределения применялись для анализа процессов эвтрофирования вод, для оцен-ки влияния на биоту загрязняющих веществ и теплового загрязнения, для изучения сукцессий, сезонных изменений и многого другого [6, 12, 16, 18, 20, 22, 23].

Заметим, что большинство моделей ранговых

n распределении содержат параметр 1n, где n1 -численность доминирующего вида,аn-общая численность организмов в сообществе [6]. Этот параметр сам по себе нередко используют в ка-честве одной из характеристик разнообразия под именем индекса Бергера-Паркера [12, 21]. Од-нако, в отличие от параметров ранговых распре-делений для отыскания индекса Бергера-Парке-ра необходимо знать обилие лишь одного, а не всех видов и не нужны вычислительные проце-ДУРЫ . В приложении к массовым данным мони-торинга индекс Бергера-Паркера имеет преиму-щество перед многими другими индексами раз-нообразия, поскольку эти данные содержат на-блюдения, в которых кроме численности всего сообщества приведена численность только од-ного доминирующего вида. Таким образом, ИН-деке Бергера-Паркера позволяет включить в ана-лиз наблюдения, отвергаемые при использовании ранговых распределений.

Отметим сразу, -риалах в силу принятых в системе биологичес-кого мониторинга методов оценки качества вод [15] представлены данные не о полных сообще-ствах видов фитопланктона, а сообществах ви-Дов-индикаторов сапробности. А именно , в ис -ходных данных приведены значения численное-тей нескольких доминирующих индикаторных видов для каждого из отделов водорослей (Chlorophyta, Cyanophyta, Euglenophyta, Bacillario-phyta и др.). При этом неучтенные виды одного из отделов могут оказаться более обильными, чем учтенные виды из других отделов, так что суммарная относительная численность учтенных видов часто оказывается менее 100%. Впрочем, в исследованиях фитопланктона почти всегда идет речь лишь о части «полного» : по обстоятельствам методического характера в анализ редко включают, , нанопланктон (хотя его численность и существенно превыша-ет численность более крупных видов). Также при обработке проб редко учитывают формы водо-рослей, подсчет которых возможен только в «жи-вых», I. . незафиксированных пробах и т. . Со-общество видов-индикаторов сапробности в он-ределенном смысле представляет собой сооб-щество " наиболее типичных" представителей фи-топланктона и, по нашему мнению, вполне мо-жет быть объектом самостоятельного экологи-ческого исследования. Однако , структурные осо-бенности сообщества видов-индикаторов требу-ют тщательного методического анализа возмож-ностей оценки видового разнообразия по таким сообществам. В частности, число видов- инди-кагоров не только отличается от числа видов в полном сообществе, но и весьма субъективно от-ражает мнение обработчика проб о достаточно-сти набора запротоколированных видов-индика-торов . Это приводит к тому, -деке видового разнообразия может быть исполь-зован . Например, оказывается невозможным кор-ректно рассчитать традиционный энтропийный индекс Шеннона-Мак-Артура-Маргалефа.

Этапу приложения характеристик разнообра-зия к оцениванию состояния экосистем должна предшествовать многосторонняя методическая проработка инструментов биоиндикации. Необ-ходим выбор : , метода оценки адекватности модели, метода оценки ее параметров.

Для характеристик разнообразия, отобранных в качестве биоиндикаторов, необходима градуи-ровка их значений на шкале «норма-нарушение», или «благополучие-неблагополучие».

Логика применения параметров ранговых рас-пределений и других индексов разнообразия в качестве биоиндикаторов состоит в интерпрета-ции различий в величине параметров как разли-чий в степени экологического благополучия или неблагополучия природной системы. Однакозна-чения параметров и индексов могут зависеть не только (а может быть, и не столько) от качества среды, но и от целого ряда факторов, не имею-щих отношения к экологическому состоянию. Среди них, например: 1) особенности обработки проб (погрешности в определении численностей клеток, особенно редких видов, отличие числа видов в индикаторном сообществе от числа ви-дов в полном сообществе); 2) возможная зави-симость параметров от сезона отбора проб (мож-но ожидать, что в периоды «цветения» фитоплан-ктона «нормальная» степень неравномерности распределения будет выше, чем в другие перио-ды), от географического расположения точки наблюдения, от климатический условий.

Материалы и методы исследования

Для апробации методов и моделей были ис-пользованы данные Роскомгидромета о фито-планктоне на 143 створах в 39 водных объектах (реках и водохранилищах) Волжского бассейна в 1979-1982, 1988, 1989, 1992, 1995, 1997 гг . (всего 698 наблюдений), а также данные о температуре и прозрачности воды на тех же створах. Данные получены из информационной системы «Эколо-гия пресных вод России и сопредельных стран» . Для оценки из-менчивости биотических показателей, обу-слов-ленных погрешностями в обработке проб были использованы данные по 50 параллельным про-бам фитопланктона залива Чупа Белого моря [5].

Отметим, что в использованных материалах в силу принятых в системе биологического мо-ниторинга методов оценки качества вод [15] представлены данные как о полных сообще-ствах видов фитопланктона (общая численность N,число видов w), так и о сообществах видов-индикаторов сапробности (число видов-индика-торов w, относительная численность видов ин- дикаторов в полном сообществе pi , индекс сап-робности сообщества). Напомним, что индекс сапробности вод по фитопланктону рассчитан по

₌2 pisi pi

формуле

, где si - индикаторная сап- робность вида i, которая определена по списку сапробных видов (например, [8]), суммирование производится по всем w видам сообщества ви-дов-индикаторов . Ранговые распределения пред-ставляют собой преобразованный набор числен-ностей: -ся первый номер, следующему по численности виду - второй и так далее до наименее обильно-го вида, который имеет номер w, совпадающий с общим числом видов в сообществе . Модель рангового распределения представляет собой формальную связь численности вида и его ран-га. Как инструмент анализа видового разнооб-разия также используется индекс Бергера-Пар-кера [21], который отражает относительную долю в сообществе наиболее обильного вида.

Анализировали экспоненциальную ( n_i n ₁ z^{i 1})

n и гиперболическую I ni iр I модели рангового распределения, где ni - численность вида i-го ранга, n1 - численность вида первого ранга, i-ранг вида, zи р- параметры моделей.

Расчет параметров осуществляли посред-ством табличного редактора Microsoft Excel 2000. Для статистической обработки данных ис-пользован статистический пакет STATISTICA 6 .

Результаты

Методическое исследование должно дать кон-

:

• 1)    Как снизить влияние погрешностей в под-счете численностей клеток фитопланктона на параметры ранговых распределений и индекс Бергера-Паркера?

• 2)    Как снизить влияние на параметры и ин-дексы их зависимости от числа представленных в пробах видов-индикаторов?

• 3)    Какая модель ранговых распределений наиболее адекватно описывает имеющиеся дан-ные? Как влияют погрешности в определении численностей клеток на степень адекватности модели ?

• 4)    Включает ли изменчивость характеристик разнообразия зависимость от факторов среды или исчерпана зависимостью от факторов, не имеющих отношения к экологическому благопо-лучию ?

При формулировке методических рекоменда-ций следует иметь в виду еще одно важное об-стоятельство. Для проведения экологического контроля (биоиндикации, статистических оценок, диагностики вредных воздействий и их нормиро- вания [7]) желательно использовать для анализа как можно больше имеющихся в базе данных наблюдений.

Снижение влияния погрешностей, возникающих при подсчете численностей клеток фитопланктона. П огрешности в подсчете численностей клеток особенно велики для малочис-ленных видов: еели для обильных видов погрешности составляют 10-20%, то для редких видов они могут достигать 100% и более [19]. Анализ ранговых распределений с точки зрения статис-тики [9] показывает, что виды, представленные в просмотренной планктонологом пробе менее чем 10 особями, р еопределены случайно и не могут быть описаны какой-либо закономерной моделью ранговых распределений.

Исходя из приведенных соображений мы пред -ложили исключить из анализируемого массива пробы, суммарная численность сообщества индикаторов в которых составляет менее 30% численности полного сообщества, а также исключить из каждой пробы виды с относительной чис-ленностью менее 5%. После исключения указанных проб для дальнейшего анализа сохранено 619 проб.

О методах оценки параметров модели. В предшествующих работах для экспоненциаль-ной и гиперболической моделей в линеаризо-ванной с помощью логарифмирования форме ln n i = ln n 1 + ( i -1) In z ; In n i = In n 1 - P In i были проведены оценки параметров по прибли-женным формулам [1] и с помощью регрессионной модели [4]. Эти предварительные проработки позволили сформулировать методические про -блемы для данного исследования. Поекольку операция логарифмирования в линеаризованных моделях искажает истинные значения парамет -ров (рис. 1 и 2), дельнейший анализ мы проводили , оп ираясь на результаты их нелинейного оценивания (рис. 3 и 4).

Исследование адекватности модели. X дек-ватность исследуемых моделей оценена при по -мощи коэффициента детерминации:

R ² =1- —

D ’ где SS - сумма квадратов отклонений предсказанных моделью значений от эксперименталь-ных; D - дисперсия экспериментальных численностей .

Далее рассчитывали долю преобладаний слу- чаев, где Rz - R22 > 0, где Rz -R, д 0 и где оба коэффициента имеют одинаковые значения Rz-R22 =0:

SIR 2*~R М iM z=S|RVR 2*| ■ iM

S| RVR2 ,„| iM

SIR2 t-R 2„| ■ iM

K - r 2

M 0

M

Здесь M - множество всех наблюдений, M+ - множество случаев, где Rzz -R22 >0; M_ - множество случаев, гдеRz -R22<0; M0 - множество случаев, где Rzz-R,2=0; M0 и M - количества соответствующих наблюдений.

Несколько более высокий коэффициент детер-минации характерен для параметра экспоненци-альной модели: доля случаев Rz -R ² >0, где составила 64%. Таким образом, едcпoнeнциaльнaя модель более адекватно описывает распределе -ние видов по обилию в бассейне р. Волги. Заметим , что отличие в степени адекватности гиперболической и экспоненциальной моделей явно не -значительно. Более того если оценку адекватности проводить с учетом ошибок в определении численностей видов, которая в среднем составляет 20% [19], то обе модели попадают в коридор ошибок, т.е. являются одинаково и полностью адекватными (рис. 5). Наряду с гиперболической и экспоненциальной была исследована модель В.Н. Максимова [9], еппроксимирующая зависимость численностей нескольких домини-рующих видов (тех, численности которых определены статистически достоверно) ди нейной функцией номера в ряду численностей, расположенных по возрастанию. И эта модель приемлемо описывает имеющиеся данные с учетом по -грешностей в подсчете численностей. Аналогичный вывод сделан и для двухпараметрических моделей ранговых распределений [1, 6]. Поэтому степень адекватности не должна служить ос -нованием при выборе между моделями.

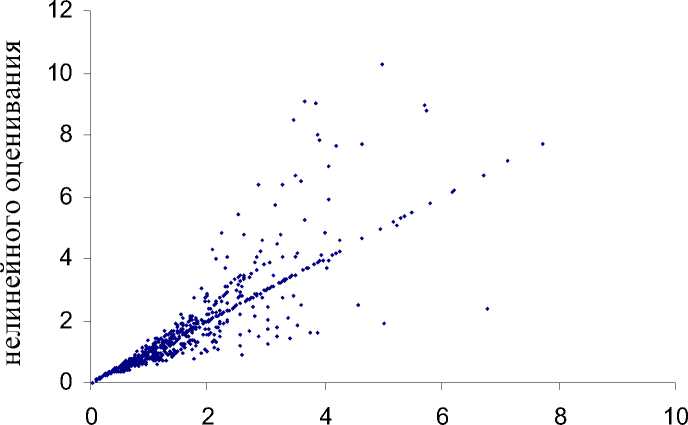
параметр р , полученный методом линейного оценивания

Рис. 1. Зависимость параметров Р гиперболического рангового распределения, полученных методами нелинейного и линейного оценивания

1.00

о н 4>

Ж к и о У ч о с

Ч S и ч м S и 1>

0.80

I I

<и S

о о о и ж

<и и S ч о щ

0.00

0.60

0.40

0.20

... -^ :^ •

С

0.00

0.20

0.40

0.60

0.80

1.00

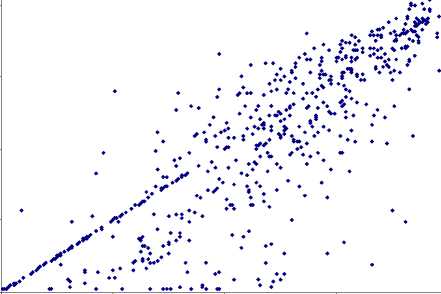
параметр z , полученный методом линейного оценивания

Рис. 2. Зависимость параметров z экспоненциального рангового распределения, полученных методом нелинейного и линейного оценивания

Исключение влияния зависимости вырав-ненности распределений от видового богат-ства. Необходимость исключить ошибки в оцен-ке параметров ранговых распределений, возни-кающие за счет погрешностей в подсчете чис-ленностей редких видов, позволяет сохранить в пробах не более 5-6 доминирующих групп кле-ток. Однако в интервале числа сохраненных в пробе видов от 2 до 6 наблюдается самая силь-ная зависимость параметров ранговых распре-делений от этого числа (другими словами , зави-симость выравненное™ видового разнообразия

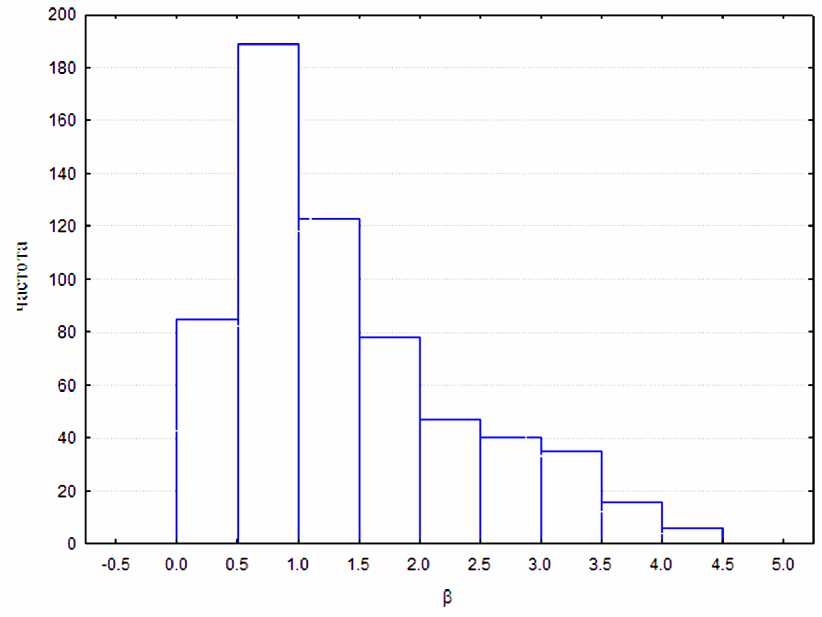
Рис. 3. Гистограмма распределения значений параметра Р, полученных методом нелинейного оценивания

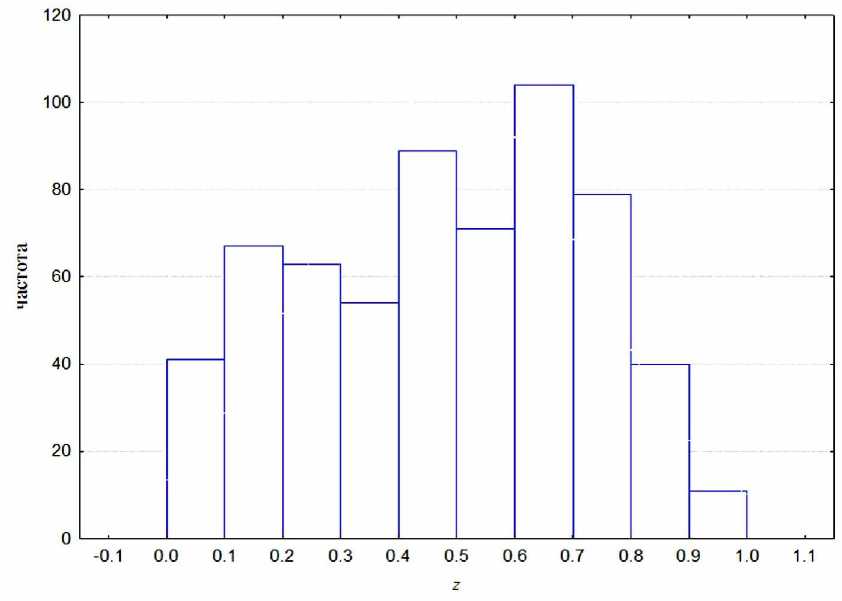
Рис. 4. Гистограмма распределения значений параметра z ^, полученных методом нелинейного оценивания

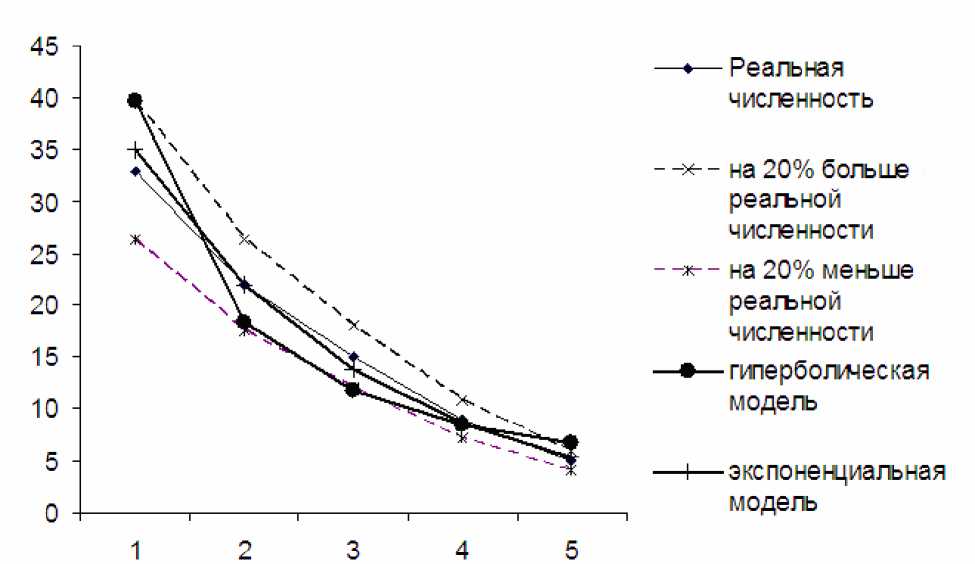
Рис. 5. Адекватность моделей рангового распределения с учетом двадцатипроцентного коридора ошибок в подсчете численностей клеток фитопланктона

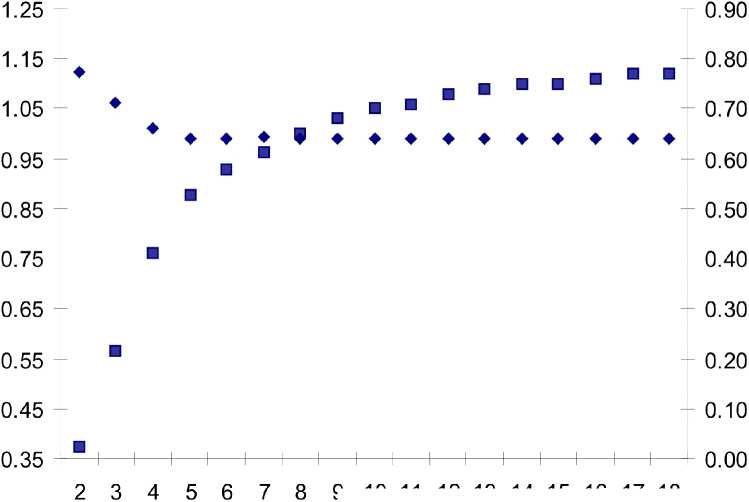
9 10 11 12 13 14 15 16 17 18

Рис. 6. Графики зависимости параметров гиперболического (Р) и экспоненциального ( z ) ранговых распределений от количества w сохраненных в пробе видов при последовательном отбрасывании последнего вида

от видового богатства). Рисунок 6 демонстри-руст зависимость параметров гиперболической и экспоненциальной моделей при нелинейном оце-нивании от количества сохраненных в пробе ви-дов при последовательном отбрасывании после- днего вида в одной из типичных проб фитопланк-тона Волги. Рисунок 7 демонстрирует зависи-мость средних значений параметров тех же мо-делей при последовательном отбрасывании пос-леднего вида по 50 параллельным пробам фито-

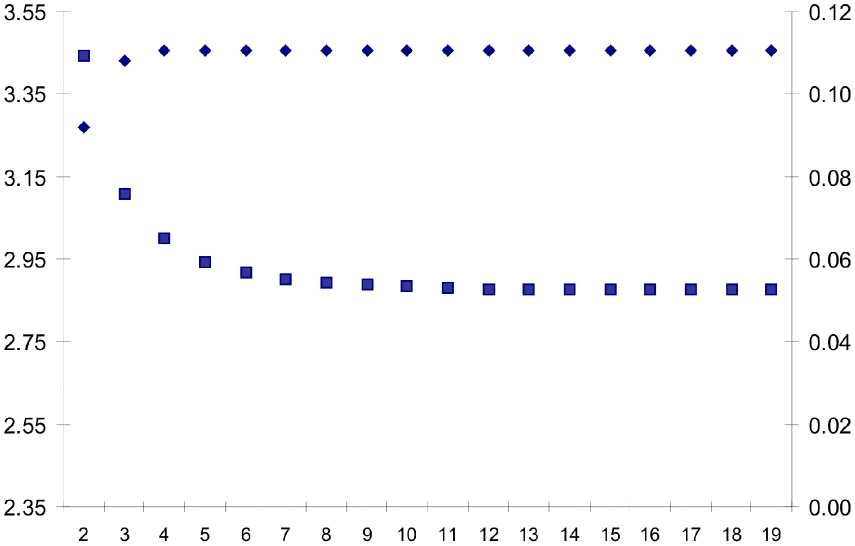
Рис. 7. Графики зависимости средних значений параметров гиперболического (Р)И экспоненциального ( z ) ранговых распределений фитопланктона из залива Чупа Белого моря

ПО 50

параллельным пробам от количества w сохраненных в пробе видов при последовательном отбрасывании последнего вида

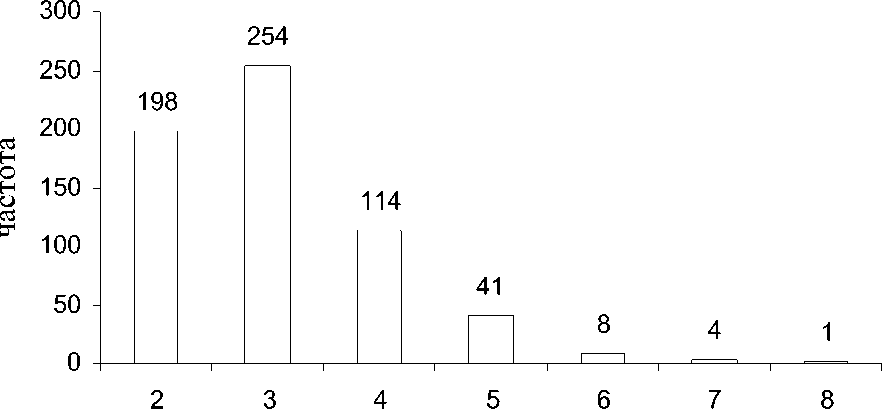
Рис. 8. Гистограмма распределения числа проб с различным числом представленных в пробе видов-индикаторов w

планктона Белого моря. Исключить указанную зависимость можно было бы, сохранив ванали-зируемом массиве только пробы, например,с w не менее 4, отбросив пятый и все последую-щие виды . Однако структура наших данных по фитопланктону Волги такова, что большинство имеющихся наблюдений содержит пробы с w =

• 2,    3 (рис. 8) и их исключение приведет к резкому сокращению доступных анализу наблюдений. Вы-ход из создавшегося положения - рассматривать в каждой пробе только два доминирующих вида. Достоинства такого рассмотрения:

n ₁ и n ₂ этих видов определены с наименьшими в

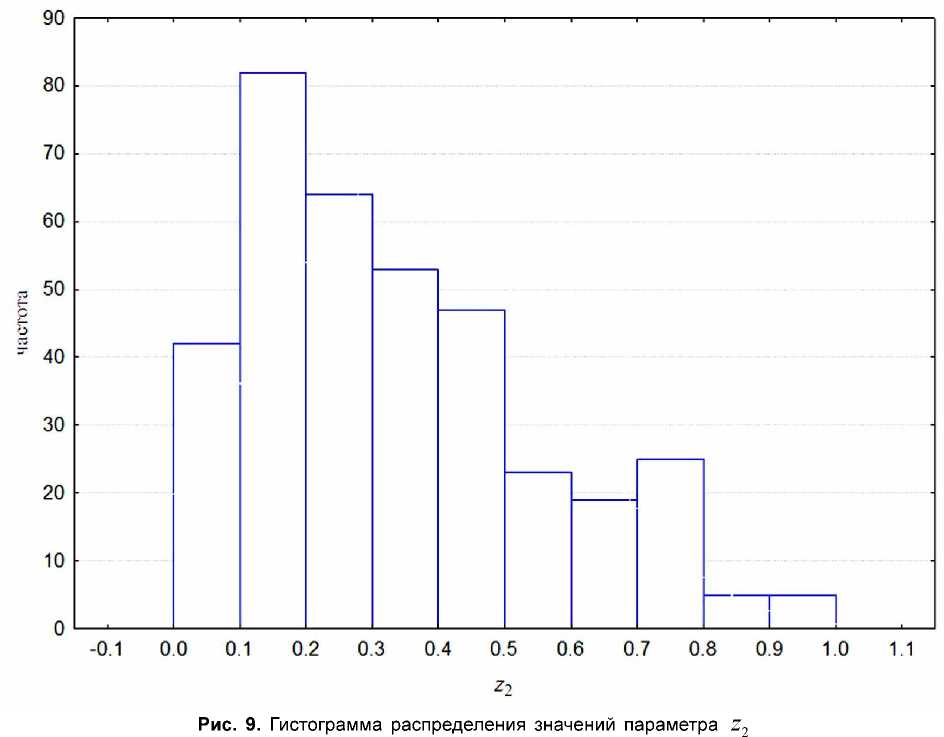
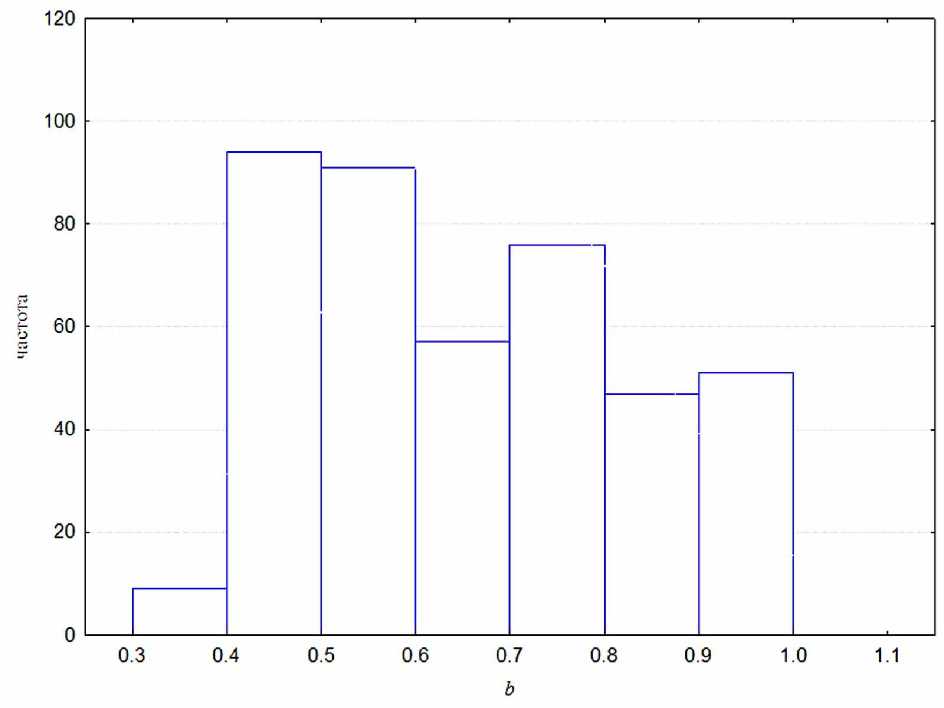
Рис. 10. Гистограмма распределения значений индекса Бергера-Паркера b

Èçвестиÿ Caìaðского наóчного центðа Ðоссийской акадеìии наóк. Т. 9, ¹ 1, 2007

1.20

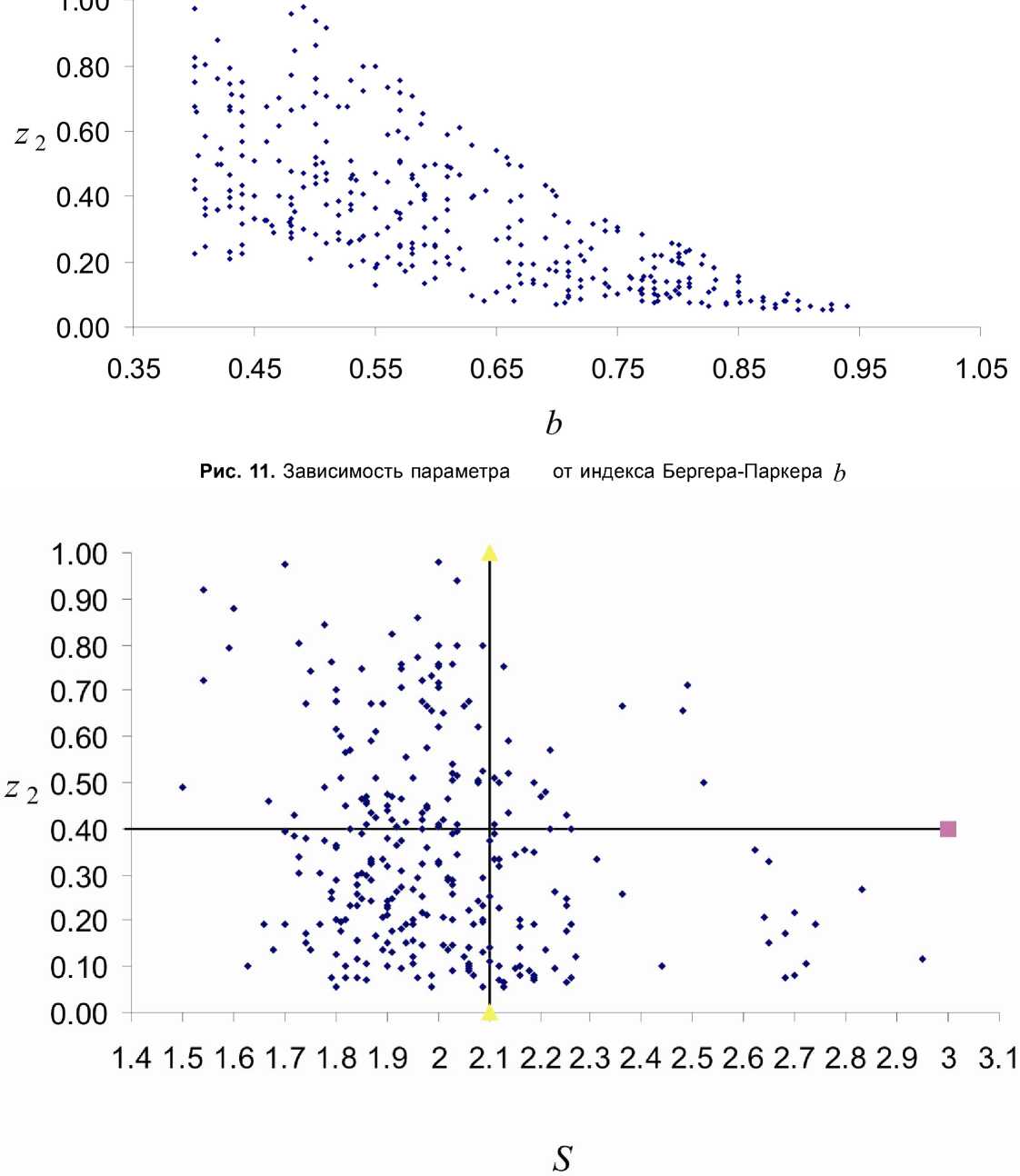
Pиc. 12. Диаграмма распределения значений пaрaмeтра z₂ и индекса сапробности S для проб бассейна Bолги, отобранных лeтом и осенью (горизонтальная линия – граница нормы для пaрaмeтра, вертикальная линия – граница нормы для индекса )

сравнении с последующим видами ошибками и для дальнейшего анализа сохранены все пробы с числом видов более одного.

Âыбор характеристик раçнообраçuÿ, адекватных имеющимсÿ данным мониторинãа. Параметры ранговых распределений двухвидовых проб могут быть рассчитаны без статистического оценивания по простым формулам

Таблица 1. Количество наблюдений N ^,среднее значение n ^,стандартное отклонение <т , коэффициент вариации е используемых параметров параллельных проб (залив Чупа Белого моря) и массива наблюдений в р. Волга

Водный объект	z 2			b			z 4
	N	n	<7	£	N	n	<7	£	N	n		£
Залив Чупа	50	0,31	0,15	0,48	50	0,51	0,08	0,16	50	0,36	0,13	0,37
Река Волга	365	0,34	0,22	0,64	425	0,66	0,17	0,26	169	0,55	0,16	0,30

Таблица 2. Основные статистические показатели параметра z ₂ в исследуемых группах

Подбассейн Тип водный объекта Сезон Среднее Количество наблюдений Стандартное отклонение Верхняя Волга Водоем Весна 0,25 33 0,19 Лето 0,36 113 0,22 Осень 0,37 66 0,24 0,35 212 0,22 Водоток Весна 0,27 12 0,18 Лето 0,34 28 0,20 Осень 0,39 19 0,26 0,34 59 0,22 Итого Верхняя Волга 0,34 271 0,22 Средняя Волга Водоем Лето 0,69 2 0,32 Осень 0,25 1 0,00 0,54 3 0,34 Водоток Весна 0,27 10 0,22 Лето 0,33 11 0,23 Осень 0,31 26 0,20 0,31 47 0,21 Итого Средняя Волга 0,32 50 0,22 Нижняя Водоток Весна 0,30 10 0,09 Лето 0,27 10 0,15 Осень 0,37 24 0,22 0,33 44 0,19 Итого Нижняя Волга 0,33 44 0,19 Все группы 0,34 365 0,22 n2                 n1

z _{2       n} и Р2 log₂¹ .

n ₁                  n ₂

Как показано выше, степень адекватности описания при имеющихся погрешностях в под-счете численностей не может служить основа-нием для выбора модели. Мы предлагаем оста- новиться на индексе z2 - параметреэкспоненци-альной модели для сообщества видов-индикато-ров . Дополнительный довод в пользу экспонен-циальной модели тот, виды сообщества видов-индикаторов совпадают с какими-либо соседними видами полного сооб- щества (первым и вторым, пятым и шестым и т. .), то индекс z2 совпадает с параметром экс-поненциального рангового распределений для пол-ного сообщества (для индекса Р2 указанное ут-верждение несправедливо). На рис . 9 приведено распределение значений индекса для фитоплан-ктонаВолги. Корреляция между параметром z2 и параметром z,рассчитанным нелинейным оце-ниванием по полному набору видов-индикаторов, равна 0,95.

Будем обозначать символом z ₄ нелинейный

Таблица 3 . Основные статистические показатели значений индекса Бергера-Паркера в исследуемых группах

Подбассейн	Тип водного объекта	Сезон	Среднее	Количество наблюдений	Стандартное отклонение
Верхняя Волга	Водоем	Весна	0,72	40	0,16
		Лето	0,67	129	0,17
		Осень	0,70	82	0,19
			0,69	251	0,17
	Водоток	Весна	0,61	12	0,15
		Лето	0,65	33	0,18
		Осень	0,66	23	0,19
			0,65	68	0,18
Итого Верхняя Волга			0,68	319	0,17
Средняя Волга	Водоем	Весна	-	-	-
		Лето	0,52	2	0,01
		Осень	0,77	2	0,29
			0,65	4	0,22
	Водоток	Весна	0,66	13	0,18
		Лето	0,71	15	0,17
		Осень	0,64	30	0,17
			0,66	58	0,17
Итого Средняя Волга			0,66	62	0,17
Нижняя Волга	Водоем	Весна	-	-	-
		Лето	-	-	-
		Осень	-	-	-
			-	-	-
	Водоток	Весна	0,49	10	0,10
		Лето	0,55	10	0,15
		Осень	0,54	24	0,09
			0,53	44	0,11
Итого Нижняя Волга			0,53	44	0,11
Все группы			0,66	425	0,17

Таблица 4. Статистические характеристики распределений параметров z2 , z4 и индекса Бергера-Паркера для массивов данных по фитопланктону Волги

Характеристика	Класс данных	Мода	Медиана	Среднее
z 2	Лето-осень	0,33	0,32	0,36
	Весна	0,27	0,21	0,26
z 4	Весна		0,57	0,55
	Лето	0,36	0,59	0,58
	Осень	0,57	0,52	0,52
	Верхняя Волга	0,57	0,56	0,54
	Нижняя Волга		0,65	0,62
b	Верхняя и Средняя Волга	0,66	0,67	0,68
	Нижняя Волга	0,43	0,48	0,52

параметр рангового распределения, рассчитан-ный по первым четырем видам всех проб, число видов в которых не менее 4. Индекс z4 должен быть менее чувствителен, чем индекс z2 , к по- грешностям в подсчете численностей за счет

-

,                    z2 ,-

.

,

(                             620-

4). - w n b 1 , nn

n

,

,-

,-

-(

).- индикаторного сообщества на полное сообщество

, -

-.-

,

-

40%,

,-

,                           .10

-

• - b-

• .               ,                       z2

( .11).-

- ледующие исследование.

Дисперсионный анализ влияния факторов, не зависящих от степени экологического бла -гополучия. Имеет место большой разброс зна- z2

.-

-

.,

, . -

-

.

n1 , n2 n ,

• b,                                  ,-

• ,-
• .-
• ,-
• .-
• z2                             -              b,-

  -

• ,-
• сионный анализ параллельных проб залива Чупа (. 1).

z2                              -- сейна реки Волги и параллельных проб залива Чупа превышает табличное значение критерия

(F= 1,83)-

( p = 0,001).        ,-

, -,

-

.                      ,-

• -                  , -,

., z2

b ,                   ,         0,48 0,16.

,- z4-

- z2 (. 1).

z ₄

, . ., -

,-

(,

-

-

).

-

, z2 b                              ,                  - ность пробы к тому или иному подбассейну или (..                           -

).

- z2

, между различными типами водных объектов

(      . 2).                ,                 «        »- ется от других сезонов при достаточно высоком (. 3).

,-

,-

-

«».

z2          «      »-

«    » «»

табличное значение критерия Фишера ( F = 8,34) при достаточно высоком уровне значимости (соответственно р = 0,003 и р = 0,004). Различие параметра между сезонами «лето» и «осень» недостоверны .

Анализ изменчивости значений индекса Бер -гера-Паркера в сезонах весна, лето, осень не показал статистически значимых различий. Отношение дисперсий индекса Бергера - Паркера подбассейна Нижней Волги к дисперсиям под -бассейна Верхней и Средней Волги превышает значение критерия Фишера при очень высоком уровне значимости. В подбассейне Нижней Волги значение индекса Бергера-Паркера ниже, чем в подбассейнах Верхней и Средней Волги (табл. 3), ото соответствует общей тенденции увеличении видового разнообразия с севера на юг [13]. Отмечены также различия индекса Бергера-Паркера в различных типах водных объектов. Однако если проводить дисперсионный анализ отли-чий различных типов водных объектов по отдель-ности в подбассейне Верхней и Средней Волги и в подбассейне Нижней Волги, то эти отличия становятся статистически не значимыми. Достоверной корреляции между характеристиками разнообразия и температурой или прозрачностью не обнаружено.

Дисперсионный анализ параметра z 4 показал достоверное отличие степени разнообразия в подбассейне Нижней и Верхней Волги (табл. 4). Также отмечено достоверно более низкое видо-вое разнообразие в осенний сезон исследований (по сравнению с весенним и летним сезонами).

z2 -гера-Паркера. Характеристики, претендующие на использование в качестве шкал для целей био -индикации, должны быть проградуированы по степени экологического благополучия-неблагополучия . М ы исходим из той предпосылки, что экологическому благополучию соответствует более высокая степень биологического разнообразия, нежели неблагополучию. Параметр z экспоненциального рангового распределения может изме-пяться в пределах от 0 до 1, как и индекс Бергера -Паркера. Низкие значения параметра z соответствуют малому разнообразию видов в со -обществе и, соответственно, высокие значения z - большому разнообразию. Для индекса Бергера -Паркера соответствие противоположное. В простейшем случае совокупность значений ин -дикаторной характеристики должна содержать два класса: благополучные значения, соответствующие нормальному состоянию биоты, и неблагополучные , соответствующие нарушенному состоянию. Задача градуировки - указать границу между этими состояниями.

Можно предложить несколько подходов к вы -бору границы:

• •    наиболее вероятное значение характеристики (мода распределения);

• •    значение, разделяющие всю совокупность значений характеристики на два равновеликих класса (медиана распределения);

• •    значение, оыбираемое согласно экспертным оценкам;

• •    верхняя (или нижняя) сраница распределения значений характеристики для сообщества, функционирующего в эталонных условиях, например , о заповедной зоне или в период с отсутствием антропогенного загрязнения и т.п;

• •    значение, обеспечивающее наилучшую корреляцию распределения индикаторной харак-теристики с распределением некоторой незави-симой от нее величины, дл о ооторой разделение на благополучный и неблагополучный классы известно и признано приемлемым.

Согласно приведенным выше результатам дисперсионного анализа, средние значения распределений параметра z ₂ достоверно различаются для наблюдений из классов «лето-осень» и «весна», о для индекса Бергера-Паркера из классов «Верхняя и Средняя Волга» и «Нижняя Волга ». П о это му и границу нормы характеристик z ₂ и b следует искать отдельно в каждом из указных классов.

В табл. 4 приведены значения моды, медианы и среднего для параметров z ₂, z ₄ и индекса Бергера - П аркера в массивах использованных нами данных по фитопланктону Волги.

В каждом классе приведенные статистичес-кие характеристики близки друг к другу. Мы предлагаем в качестве границы между благопо-лучными и неблагополучными значениями при -нять медиану соответствующих распределений. «Медианное» значение границы можно попытаться уточнить с помощью согласования классов благополучия и неблагополучия индикаторных характеристик с аналогичными классами обще -принятой классификации качества вод по сапроб-ности. Интерполяция на два класса качества «благополучие» и «неблагополучие» шкалы сап-робности из классификатора классов качества вод Роскомгидромета [14] п озволяет принять в качестве граничного между «благополучием»и «неблагополучием» значение сапробности, рав-ное 2,1. То есть, качество воды в пробах, где ин-деке сапробности по фитопланктону менее или равен 2,1, признается благополучным, в пробе, где индекс сапробности более 2,1 - неблагопо-лучным .

На рис. 12 приведена диаграмма распределе-ния значений индекса z ₂ и сапробности для проб бассейна Волги, отобранных летом и осенью .В случае идеальной согласованности между инди-кагором z ₂ и индикатором S ' на диаграмме квад ^-ранты « b » и « c » должны быть пустыми (небла-гополучие по z ₂ соответствует только неблаго-получию по S , благополучие - так же). Индекс сапробности по определению регистрирует толь-ко органическое загрязнение вод. Параметр же z ₂ как индикатор стрессовых воздействий дол-жен испытывать влияние всех других - неорга-нических химических, климатических, гидрофи-зических факторов, нарушающих экологическое благополучие. Поэтому в квадранте « c » вполне могут быть наблюдения с благополучным по органике, но неблагополучным по другим факто-рам качеством вод, что влечет благополучные значения индекса сапробности, но неблагополуч-ные - параметра z 2 . Квадрант « b » не должен со-держать наблюдений, поскольку наличие органи-ческого загрязнения (неблагополучие по сапроб-ности) должно приводить к снижению разнооб-разия,т. . к неблагополучным значениям пара-метра, и все такие наблюдения должны попадать в квадрант « d ». Таким образом, граница нормы для параметра z ₂ (горизонтальная линия на ди-аграмме рис. 12) должна проходить так, чтобы квадрант « b » содержал как можно меньше на-блюдений. Формальный критерий поиска грани-цы нормы с учетом ее «близости» к медиане рас-пределения может быть выражен требованием :

а n ( a ) +       n ( a + b )

n(a +b) 12 n(a +b+c+ d) , где n( x) — количество точек в соответству-ющих квадрантах диаграммы,а и у- нормиро-вочные множители.

Для границы нормы параметра z2 в массиве «лето-осень» получили величину около 0,4, в мае-сиве «весна» - около 0,3. При этом степень пра- n(a)

вильности —---— утверждения «если значение

n ( a + b )

параметра z ₂ благополучно, то и значение сап-робности благополучно» равен, соответственно, 0,86 и 0,62, а критерий близости к медиане рас- n ( a + b )

пределения ¹₂ n ( a +b+c+ d ) ' равен ^, соответствен ^-но, 0,72 и 0,68. Индекс Бергера-Паркера оказал-ся не чувствительным к органическим загрязне-ниям, индикатором которых принят индекс сап-робности . Для него граница нормы принята со-^: для наблюдений в Верхней и Средней Волге -около 0,7, для Нижней Волги - около 0,5.

Выше было отмечено, что применениеиндек-сов сапробности обладает рядом недостатков. Эти недостатки, по-видимому,                 - зовать представления о сапробности для граду-ировки характеристик разнообразия в тех облас-тях , где эти представления адекватны , с тем, чтобы применять параметры разнообразия и в тех областях, где представления о сапробности

.

Аналогично индексу сапробности для граду-ировки параметров разнообразия могут быть применены и другие характеристики загрязнения, например, уровни вредных воздействий, для ко-торых известна граница между допустимыми и недопустимыми значениями. Указанный подход будет испытан для градуировки параметра z ₂ и индекса Бергера-Паркера в дальнейшей работе.

Заключение

Проведенный методический анализ возмож-ности использования в целях биоиндикации коли-чественных характеристик видового разнообра-зия фитопланктона, полученных по многолетним данным государственного экологического мони-торинга пресных вод России, позволяет сформу-:

• 1)    Во всех пробах следует оставить не более двух доминирующих видов. Из дальнейшего ана-лиза следует исключить пробы, суммарная чис-ленность индикаторного сообщества в которых составляет менее 30%.

• 2)    Следует рассчитать следующие характе-ристики видового разнообразия:              -

• n ненциального рангового распределения z2   2

n ₁

и индекс Бергера-Паркера b n1 n, где n1 - чис- ленность первого доминирующего вида, n2 - чис- ленность второго вида иn-суммарная числен-ность сообщества.

• 3)    Для исследованных в данной работе фито-планктонных сообществ Волги граница между благополучными и неблагополучными состояни-ями составляет:      z ₂ в классе «лето-осень» -

• около 0,4, в классе «весна» - около 0,3; для bв классе «Верхняя и Средняя Волга» около 0,5; в классе «Нижняя Волга» - около 0,7. Положение границы нормы может быть уточнено привлече-нием данных, позволяющих провести дополни-тельную процедуру градуировки.

• 4)    Для исследованных в данной работе фито-планктонных сообществ Волги изменчивость параметра z ₂ и индекса Бергера-Паркера, по-ви-димому,                        , связанным с

погрешностями в определении численностей ви-Дов, разбросом температуры и прозрачности воды, возможными различиями разнообразия в водотоках и водоемах.

• 5)    Возможность применения индекса z ₄ тре-бует дополнительного исследования. Среди воз-можных преимуществ этого индекса в сравне-нии с параметром z ₂ - более низкая чувствитель-ность к погрешностям в определении численно-стей видов . Среди недостатков - недоступность анализу проб с одним, двумя и тремя видами и, ВОЗМОЖНО , более низкая, чем у z ₂ и b , чувстви-тельность к воздействиям среды.