Методические аспекты изучения состояния гомеостаза животных по параметрам хемилюминесцентной кривой

Сложные системы гомеостаза сельскохозяйственных животных в искусственно созданных условиях постоянно испытывают давление антропогенного фактора. Существуют различные способы описания состояния таких систем и их структуры на различных уровнях: от молекулярного до популяционного. Однако традиционные зоотехнические методы не могут обеспечить надежность и оперативность контроля скорости и качества адаптационных изменений, вызванных различными эндогенными и экзогенными факторами. При этом актуален поиск индикаторов нарушения гомеостаза, его ранних стадий, когда еще не наступила деградация сложной системы, и патологический процесс может быть обратимым. Таким показателем, по нашему мнению, может служить резерв реактивности фагоцитарного звена иммунокомпетентной системы, определяющей состояние специфической и неспецифической резистентности организма.

Комплексный подход, объединяющий индикаторы состояния сложных систем (показатели хемилюминесцентной (ХЛГ)) с традиционно используемыми селекционными показателями, обеспечит создание научно обоснованных рекомендаций по сохранению, использованию, управлению и восстановлению генофонда сельскохозяйственных животных.

Опираясь на положительный опыт применения хемилюминисцентного анализа (ХЛ-анализ) в изучении закономерностей формирования механизмов иммунологического статуса при развитии патологического процесса [1]; в оценке изменений адаптационного потенциала людей при различных функциональных нагрузках [2]; в оценке влияния оксидативного стресса на иммунитет и старение организма [3], подобные исследования проводятся и на сельскохозяйственных животных. Исследовательский коллектив изучает возможности применения ХЛ-анализа в животноводстве в качестве одного из дополнительных индикаторов при скрининге состояния гомеостаза в условиях адаптивной и неадаптивной интенсификации в животноводстве. В связи с этим необходимо найти ответы на ряд проблемных вопросов. Зависят ли параметры хемилюминесцентной кривой от генотипических факторов (порода, линия, экогенез)? Влияют ли паратипические факторы (возраст, сезон) на параметры хемилюминесцентной кривой? Какая изменчивость параметров хемилюминесцентной кривой выше: групповая или индивидуальная? Существуют ли взаимосвязи между параметрами хемилюминесцентной кривой и показателями воспроизводительных способностей, если да, то какова эта зависимость? Сохраняются ли выявленные взаимосвязи в течение жизни, каковы доверительные интервалы этой взаимосвязи, передаются ли они по наследству? Имеют ли выявленные закономерности видовую принадлежность?

Основной задачей является выработка методических подходов (а в последующем — алгоритма) к обработке полученных данных.

Объектом исследования были быки-производители ОАО «Красноярскагроплем». Материалом для исследования послужили клетки периферической крови и спермопродукция быков. В ходе исследовательской работы была выполнена комплексная оценка особенностей спермопродукции с учетом возрастных, сезонных изменений, также был произведен учет качества спермы в зависимости от породы и места рождения быков-производителей.

Методы исследования . Оценивали функциональную активность клеток крови быков при антигенной стимуляции in vitro. Основной критерий – кинетика генерации активных форм кислорода (АФК), регистрируемая микрометодом люминолусиленной хемилюминесценции с использованием аппаратурнопрограммного комплекса «Хемилюминометр CL-3604» – ПЭВМ (СКТБ «Наука»). Время записи хемилюминесцентной кривой составляло 180 мин при температуре в регистрационной камере +37^оС. О кинетике генерации АФК в системе клеток цельной крови быков судили по параметрам хемилюминесцентной кривой, принимая во внимание наиболее информативные: амплитуду максимальной активности хемилюминесцентной реакции ( I max , имп/с), время достижения максимума ( T max , мин) и площадь под кривой хемилюминесценции ( S – имп. за 180 мин), определяющей общее количество АФК, генерируемых клетками за время записи хемилюминесцентной кривой.

Далее исследуются вопросы о наличии и форме взаимосвязей между параметрами хемилюминесцентной кривой и генотипическими (порода, линия, экогенез), паратипическими факторами (возраст, сезон), показателями воспроизводительных способностей. Стоит отметить, что любые данные, представляющие собой количественные характеристики таких сложных систем, формируются под воздействием множества факторов, не все из которых доступны внешнему контролю.

Таким образом, с точки зрения математики рассматриваются случайные величины Х (оказывающие влияние параметры, факторы или показатели) и Y (зависимая величина, т.е. параметры на которые оказывается влияние), а также зависимости одних параметров ( Y ) от других ( Х ). Так, амплитуда максимальной активности хемилюминесцентной реакции ( I max – имп/с), время достижения максимума) ( T max – мин) и площадь под кривой ( S – имп. за 180 мин) будут рассматриваться как переменная Y, а показатели воспроизводительных способностей, генотипические и паратипические факторы – в качестве переменной Х.

Как правило, при решении вопросов о наличии взаимосвязи в качестве оценки степени зависимости одних величин от других используют коэффициент корреляции и с его помощью строят линейные модели. Однако эта простейшая характеристика связи не является исчерпывающей мерой зависимости между X и Y . На самом деле, коэффициент корреляции r xy может обращаться в нуль даже для зависимых X и Y и не равняться 1 для величин, связанных нелинейной функциональной зависимостью.

Учитывая, что структура исследуемых зависимостей может носить нелинейный характер, то целесообразно строить непараметрические модели [4] и использовать методологию дисперсионного анализа [5] для исследования стохастических связей.

Так, в качестве меры зависимости, в том числе и нелинейной, между двумя случайными величинами X и Y используют дисперсионное (корреляционное) отношение [5]

₂ = DM(Y | X )

^x d (у )     ,                          (1)

где DM(Y | X ) = M [ M(Y | X ) - M(Y ) ] ² – дисперсия условного математического ожидания; (2)

D(Y) – дисперсия случайной величины Y;

M(YlX) — условное математическое ожидание случайной величины Y при данном х ;

M(Y) – математическое ожидание случайной величины Y.

Дисперсия условного математического ожидания DM(Y|X) характеризует ту часть флуктуаций переменной Y , которая вызвана влиянием переменной X . Поэтому иногда дисперсионное отношение называют мерой определенности, вводят также меру неопределенности

_ ₂    MD(Y | X )

^{П y|x} =     D (Y )    ’                                   ⁽³⁾

где MD(Y|X) – средняя условная дисперсия характеризует ту часть общей дисперсии переменной Y , которая вызвана совокупностью всех остальных факторов, кроме влияния переменной X .

Можно доказать теорему разложения дисперсии выходной переменной [5], согласно которой

D(Y)=DM(Y|X)+MD(Y|X) .                                   (4)

Из приведенной выше трактовки дисперсии условного математического ожидания DM(Y|X) и средней условной дисперсии MD(Y|X) следует, что дисперсию условного математического ожидания DM(Y|X) можно использовать в качестве характеристики степени связи между входной и выходной переменными, а математическое ожидание условной дисперсии MD(Y|X) – в качестве характеристики степени неопределенности, неидентичности, количественно характеризующей неадекватность данной модели из-за «неучета» остальных факторов, кроме X .

Учитывая теорему (4) и приведенные определения (1) и (3), получаем, что

2   . —2

ⁿ y\x + ^П уХ

DM(Y | X ) + MD(Y | X ) _ 1 D (Y )    +    D (Y )    =

2 ₊ MYY\X) Перепишем соотношение в виде П ух +    d (y )     = ¹ •

.

Для того чтобы п ² _ 1 необходимо и достаточно, чтобы y|x ,

MD(Y | X) _ M [Y - M(Y | X)]2 _ 0, то есть, чтобы y = M(Y|x). Это значит, что у и х связаны функциональным соотношением y = f(x).

Из этого вытекает, что п2_Х = 0 в том и только в том случае, если M(Ylx)=M(Y) при любом х . Отсюда следует, что п 2_Х = О , если X и Y независимы, но обратное неверно.

В общем случае 0 <  Ц у_x <  1 . При наличии функциональной связи между Х и Y дисперсионное отношение равно единице. В случае отсутствия зависимости П у_х = 0 .

Таким образом, дисперсионное отношение n yx можно интерпретировать как количественную характеристику меры определенности случайной величины Y по значениям случайной величины X .

Из определения следует, что в отличие от коэффициента корреляции, дисперсионное отношение не является симметричным, то есть П у_х ^ П 2у . Это связано с тем, что при вычислении дисперсионного отношения используется условное математическое ожидание, которое является несимметричной функцией.

Сложность рассматриваемого вопроса состоит в необходимости оценивания регрессии M(Y | X ) в случае, когда параметрический вид последнего неизвестен. Регрессию можно оценить различными способами и от качества этих оценок будет существенно зависеть качество оценки дисперсионного отношения. В данной работе в качестве оценки регрессии предлагается использовать непараметрическую модель [4].

Если для построения параметрической модели нет достаточных априорных, то задача идентификации состоит в оценивании функции на основе выборки в форме ys _ fs (x, У,, xi),

где y i , x i – измерения случайных величин Y и X соответственно.

С точки зрения математической статистики, поставленная задача представляет собой задачу оценивания случайной величины Y по наблюдаемым входным значениям х случайной величины X , т. е. в построении модели, которая имеет вид y = y ( x ) , где У - некоторая оценка искомой истинной функции о = f ( x ) . Ошибка оценки У искомой функции о = f ( x ) представляет собой случайную величину е (х) . Обычно точность оценки У характеризуют средним квадратом ошибки при данном х :

Средний квадрат ошибки оценки У будет минимальным, если за оценку У принять условное математическое ожидание случайной величины Y при данном х , т. е.

а эта зависимость представляет собой среднюю регрессию Y на х . Модель, определяемая регрессией Y на х , называется моделью средней регрессии, или просто регрессионной моделью.

По определению условного математического ожидания, используя оценки Розенблатта-Парзена, построим непараметрическую регрессионную модель (6), (7) в одномерном случае.

^y S ^{( x} , C Sx ) =

S      (

t Уф

i = 1        V

—

Sx

J

S

£ ф

x - x i

i = 1     V

Sx

J

где      yi, Xi - измерения случайных величин Y и X соответственно (значения параметров хемилюминесцентной кривой, показателей воспроизводительных способностей, генотипических и паратипических факторов);

y s - оценка Y в зависимости от х;

S - объем выборки;

Ф( u)  - колоколообразная функция, в данной работе использовалась следующая колоколообразная функция ф( u ) =

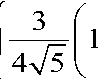
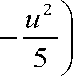
, при | u | <

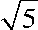
0, при | u | > 55

C sx - параметр размытости (параметр, характеризующий «гладкость» построенной модели).

Значение параметров размытости оказывает существенное влияние на качество работы регрессионных моделей при использовании выборок конечного объема S . Поэтому параметры размытости должны удовлетворять определенным условиям сходимости [4].

В многомерном случае, когда случайная величина X представляет собой совокупность нескольких параметров, то есть является вектором X = ( x\x ²,..., x k ) , непараметрическую регрессионную модель (6), (7) аналогично можно представить в виде

^{У (} x , ^C Sx ) =

Sk

Z у , П ф i = 1 j = 1 к

—

Sx

j A

Sk

Zn® i =1 j =1

—

j ^A

к

Sx

где k - размерность вектора X = ( x ¹, x ²,

...,

k x );

x , - измерения переменной X^ вектора X = ( x ¹, x ²,

...,

x^k ) ;

C S _x - параметр размытости для переменной x^ вектора X = ( x ¹, x ²,

...

, x^k ) .

Далее получаем непараметрическую оценку дисперсионного отношения, используя определение

дисперсионного отношения (1), определение непараметрическую регрессионную модель для

1 S^

математического ожидания M^{( Y} ) =   Z ^yi

S i = 1

дисперсии условного математического ожидания (2), одномерного случая (8) и (9) для многомерного, оценки

1    ( и дисперсии D (Y) = q Zl У, S i=1 к

—

7 Z Ук

S k = 1

к2

.

7

Таким образом, дисперсионное отношение в одномерном случае имеет следующий вид:

St

St 7=1

(

Z уф i =1

У xi

x

j

A ²

S

n 2

y|x

к

i = 1

к C s

x

—

x

j

A

S

4 Z y,

S i = 1

к  CS  7

1 ST-

SS

1 Z\y—1Z y.

S i = 1

A ²

,

i

к

S~

k

где St – некоторая константа, количество шагов дискретизации.

И аналогично непараметрическая оценка дисперсионного отношения в многомерном случае имеет вид

S

k

выше.

7x1 ,

■. ^x k

St

j = 1

Z У, П ф

—

7 A

к

i = 1

j = 1

к

Sx

S

S

k

—

j A

Z у,

i = 1

к

i = 1 j = 1

к

Sx

1 Z l y , S

i = 1 к

—

1 S S ^{Z y}‘

j = 1

2

,

где все обозначения, функция Ф и параметр размытости С S в (10) и (11) имеют тот же смысл, что и

Таким образом, предполагается, что расчет дисперсионного отношения позволит судить о наличии зависимости между параметрами хемилюминесцентной кривой и факторами (как генотипическими, так и паратипическими).

Применение предложенных оценок будет способствовать решению вопроса о взаимосвязи между параметрами хемилюминесцентной кривой и показателями воспроизводительных способностей быков (концентрация, средний объем эякулята, брак и др.), а построение непараметрических моделей будет говорить о том, какова эта зависимость.

Кроме того с помощью дисперсионного отношения предполагается выяснить сохраняются ли выявленные взаимосвязи в течение жизни и передаются ли они по наследству.