Методические аспекты корреляционно-регрессионного анализа при вычислении генетического веса эритроцитарных аллелей в популяциях молочного скота

ствами, болезнями, особенностями тех или иных пород и пр. [6, 11, 12, 14, 16 и др.]. Интересные данные были получены Романенко Г.А. при изучении генетических маркеров в селекции уральского чёрнопёстрого скота [19], Боевым М. М. - при изучении групп крови у скота в Курской области [2], Букаро-вым Н. Г. - в Московской области [5] и т. и.

Согласно исследованиям С. Исламовой с соавторами [9], у изученных симменталов отсутствовали антигены Р₂, Y_b А'₂, Р'₂, а Т₂ имел наибольшую концентрацию, однако в Башкортостане также часто встречаются факторы W и F, не обнаружены Z', R_1; X], М', У'_ь R' и пр. [22]. При этом факторы С', С₂, Е, L, L', R₂, X] и Х₂ встречались у чёрно-пёстрых коров, выбраковываемых и по старости, и по причинам различных заболеваний, частота антигена А! у коров-долгожительниц составляла 0,0566, а при болезнях сердца, эндометрите и пневмонии - до 0,1818.

Наряду с большим количеством противоречивой информации о маркерной способности тех или иных аллелей групп крови, в более современной работе, опубликованной в журнале «Сельскохозяйственная биология» Н. В. Проскуриной, Т. И. Тихомировой, Е. А. Гладырь и др, (2007) было доказано, что при небольших генетических различиях между внутрипо-родными структурами более информативны микросателлиты [18].

Вполне очевидным стало то, что полагаться на маркерные способности эритроцитарных аллелей в настоящее время весьма опрометчиво, учитывая даже явления плейотропии, сцепления генов, гетерозиса и пр., сущность которых в учебнике «Генетика» вполне весомо объяснил профессор Бакай А. В. с соавторами [1]. В подтверждение сложных генетических взаимосвязей следует привести работу Н. Г. Букарова, , где сказано, что гены, кодирующие систему ЕА F (Erythrocyte Antigen F), находятся на 15 хромосоме, а открытие в этой системе антигена V' позволяет лучше понять сущность эволюции скота [5].

Прямо и косвенно превосходство цитогенетического анализа, ДНК-анализа и пр. генетических методов над иммуногенетическим анализом подтверждают работы Калязиной 7'.5.(2012) [10], Яковлевой А.Ф. (1998-2000) [10] и др. Используя достижения современной науки, отдельные отечественные работы [25] и основная масса иностранных работ построены в настоящее время на подробном, научно обоснованном генетико-статистическом анализе [29-40 и др.]. В частности, многие иностранные работы посвящены геномной оценке [29-31, 34], оценке генетических параметров [32-33, 37, 38]. В своём труде «Power of daughter and granddaughter designs for determining linkage between marker loci and quantitative trait loci in daily cattle» Weller JI, Kashi Y, Soller M. (1990) [35] сказал о маркерных локусах и количественных признаках.

Wiggans GR., Misztal I., Van Tassell С.Р. в работе «Calving ease (co)variance components for a sire-maternal grandsire threshold model» (2003) используют для более обоснованных выводов сложные статистические методы, включая ковариации [39].

Наряду с этим группа учёных во главе с Wiggans GR. (2009) в работе «Selection of single-nucleotide polymorphisms and quality of genotypes used in genomic evaluation of dairy cattle in the United States and Canada», опубликованной в США, говорят о нуклеотидном полиморфизме и его взаимосвязи с продуктивными признаками молочного скота [40].

Всё это подтверждает необходимость более подробного анализа генетического полиморфизма, включая иммуногенетический полиморфизм, выявление математических закономерностей распространения, дрейфа и концентрации аллелей. Данной проблеме посвящена данная работа, представляющая собой некоторые экспериментальные подходы биометрии при анализе генетического веса аллелей в популяции молочного скота.

Материалы и методы исследований

Для решения обозначенной проблемы нами была предпринята попытка прогноза количества аллелей определённой концентрации по генетическому весу отдельного аллеля в популяции с целью выявления общебиологических закономерностей в стадах молочного скота. Для анализа было взято поголовье быков-производителей голштинской породы, семя которых реализовалось в последние 10 лет на племенных ап+ЬЦ — = Иу; aS— + ЬЕ—v = S— X XX X предприятиях РФ. В исследованиях впервые было введено понятие генетического веса эритроцитарных аллелей, вычисленного по собственной формуле:

Gwe = Ei:XE, где Gwe- генетический вес аллеля;

Ej- количество положительных реакций на аллель / в популяции;

ЕЕ - сумма всех положительных реакций! на все аллели в популяции.

Данный подход был предпринят в качестве эксперимента с целью более чёткого понимания иммуно-генетических процессов, распространения, дрейфа и элиминации аллелей. Отличия градаций генетического веса аллелей составляли 0,2: от 0,2 до 2,2. В зависимости от спада количества аллелей и роста их генетического веса для выражения математических зависимостей использовались уравнения нелинейной регрессии:      _________________________

- ь

Ух = а + -___________х нелинейная регрессия (гипербола первого порядка);

- Ь

Ух = а + — ________ х нелинейная регрессия (гипербола второго порядка);

—        I      С

= a + b- х+ —

_________х_

нелинейная регрессия (гипербола первого порядка с тремя неизвестными);

- ь

У_х = а + — __________ х нелинейная регрессия (гипербола третьего порядка).

Для построения уравнений регрессий пользовались учебником Г. Ф. Лакина («Биометрия»), Стандартная статистическая обработка данных проходила в компьютерной программе «Microsoft Excel».

Результаты исследований и их обсуждение

В результате предпринятого аналитического эксперимента было установлено, что 16 аллелей в выборке имели генетический вес 0,2, с увеличением генетического веса до 0,4-0,8 количество аллелей, имеющих схожий вес, значительно падало - до 3-6, и только один аллель имел генетический вес 2,2 (см. таблицы 1-4).

Для определения параметров а и b при построении уравнения гиперболы первого порядка была решена система следующих нормальных уравнений:

if    1    у  М

, откуда следует 3 — — SyS —-— S— S— ;

DV   х    х х)

1 (      у           1 )                    1

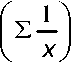
- определитель системы;

Ь = — \ ПИ^-ИуИ- где D=nH^--

DV  X     х)          х2

х - значения независимой; у - значения зависимой переменных величин.

Таблица 1 - Вычисление при построении уравнения гиперболы первого порядка для прогноза количества антигенов по их генетическому весу
п	X	У	х2	У X	X	1 х2	Прогноз: ух
1	0,2	16	0,04	80	5	25	14,7718
2	0,4	5	0,16	12,5	2,5	6,25	7,723675
3	0,6	6	0,36	10	1,666667	2,777778	5,3743
4	0,8	3	0,64	3,75	1,25	1,5625	4,199613
5	1	3	1,00	3	1	1	3,494801
6	1,2	3	1,44	2,5	0,833333	0,694444	3,024926
7	1,4	4	1,96	2,857143	0,714286	0,510204	2,689301
8	1,6	3	2,56	1,875	0,625	0,390625	2,43 75 82
9	1,8	3	3,24	1,666667	0,555556	0,308642	2,241801
10	2	1	4,00	0,5	0,5	0,25	2,085176
11	2,2	3	4,84	1,363636	0,454545	0,206612	1,957028
2	-	50	-	120,0124	15,09939	38,9508	50
Из таблицы 1 были получены вычисления D, а и Ь: 1 ( 1V                      7 О=лХ —- X- = 11-38,9508-15,099392 =428,4589-227,9916 = 200,567; X" к х) а = Д | XvE Д- -X — X - | =----1----(50 ■ 38,9506 -120,0124 • 15,09939 ) = 0,675551; DV х2 х х) 200,4674 х

Ь = -Ц /?Х^-ХуХ-!-| =----i----(11 • 120,0124 — 50 • 15, х х) 200,4674 х

= 200,567(1320,137 - 754,9693) = 2,81925.

В результате вычислений была получена формула для построения теоретической линии количества аллелей в зависимости от их генетического веса:

ух =0,675551 +

2,81925 х

нелинейная регрессия (гипербола первого порядка).

Например,

если х=0,2, то

ух = 0,675551 +

2,81925 0,2

= 17,7718 (см. прогноз в таблице 1). Сумма

у _х =50 подтверждает правильность вычислений.

Аналогично для нахождения параметров а и Ь в гиперболе второго порядка была решена следующая систему нормальных уравнений:

ап+ = Ху; аИ—7 + Ь^ —т = Х-Д , откуда следует:

X"          X" X X

a^-TsysT-sTs-rb Ь = Ъ ^4-2У£Т ,гд=О = пеТ-- sT -

DV х х х ) DV х X")          х V X")

определитель системы.

1 Y

D= лХ —- X — =7439,471-1517,165 = 5922,306;

х V х )

Таблица 2 - Вычисление при построении уравнения гиперболы второго порядка для прогноза количества антигенов по их генетическому весу

п	X	У	2 X	4 X	У	1	1	Прогноз: ух
1	0,2	16	0,04	0,0016	400	25	625	16,035
2	0,4	5	0,16	0,0256	31,25	6,25	39.0625	6,0225
3	0,6	6	0,36	0,1296	16,66667	2,777778	7,716049	4,168333333
4	0,8	3	0,64	0,4096	4,6875	1,5625	2,441406	3,519375
5	1	3	1,00	1	3	1	1	3,219
6	1,2	3	1,44	2,0736	2,083333	0,694444	0,482253	3,055833333
7	1,4	4	1,96	3,8416	2,040816	0,510204	0,260308	2,95744898
8	1,6	3	2,56	6,5536	1,171875	0,390625	0,152588	2,89359375
9	1,8	3	3,24	10,4976	0,925926	0,308642	0,09526	2,849814815
10	2	1	4,00	16	0,25	0,25	0,0625	2,8185
11	2,2	3	4,84	23,4256	0,619835	0,206612	0,042688	2,795330579
	-	50	-	63,9584	462,696	38,9508	676,3156	=50

а = —(| =--------(50 • 676,3156 - 462,696 • 38,95

D< х х- х2) 5922,306 v

= 0,00017(33815,78 -18022,37935) = 2,685;

b = ^nZ^- -ZyL^ = 0,00017(11 • 462,696 - 50 • 38,9508) = 0,534.

В результате вычислений была получена вторая формула для построения теоретической линии коли- чества антигенов в зависимости от их генетического веса:

ух = 2,685 +

0,534 %²

нелинейная регрессия (гипербола второго порядка).

Таким образом, даже без вычисления корреляции было видно, что во втором случае фактические и эм- лирические данные совпадают сильнее, а следовательно, для прогноза количества антигенов по их весу в популяции лучше использовать гиперболу второго порядка.

Для нахождения параметров а и Ь в гиперболе третьего порядка также была решена система нормальных уравнений: