Методические аспекты оценки остаточной прочности поврежденных корпусных конструкций

Связи корпуса, являющегося сложной пустотелой балкой, подкрепленной набором в различных направлениях, участвуют одновременно в нескольких видах деформаций. Эти деформации вызываются как общим изгибом корпуса, так и местным изгибом перекрытий, набора, пластин. Кроме того, задача обеспечения прочности корпусных конструкций осложняется тем, что прочность связей корпуса изменяется во времени вследствие неизбежного износа и остаточной деформации. Причем эти изменения зависят не только от времени, но и от особенностей конструкции корпуса, условий его эксплуатации. Таким образом, сложность нагружения конструкции, комплексная работа ее связей, влияние времени и окружающих условий приводит к тому, что оценка прочности корпуса затруднена и требует пристального изучения.

Как правило, на стадии проектирования несущие силовые конструкции водоизмещающих транспортных судов рассчитывают на воздействие максимальных статических нагрузок. Однако в процессе эксплуатации данные конструкции могут подвергаться значительным повторнопеременным динамическим нагрузкам, приводящим к возникновению усталостных повреждений. Постепенное накопление усталостных повреждений с течением времени приводит к образованию и распространению трещин, а в конечном итоге — к разрушению корпусных конструкций, которое может иметь самые трагические последствия для транспортного судна и его экипажа.

Основными источниками динамических нагрузок являются следующие:

• —    работа элементов пропульсивного комплекса судна (главного двигателя, валопровода и судового движителя) и других силовых агрегатов, приводящая к возникновению локальных упругих, а в некоторых случаях и упругопластических вибраций. Современные транспортные суда оснащаются разнообразными механическими устройствами, в состав которых входят механизмы с возвратно-поступательным движением звеньев (поршневые машины, кулачковые механизмы и т. д.), а также элементы, совершающие вращательное движение (валы, элементы передач, ротационные механизмы и т. д.). Действие сил инерции поступательно движущихся и вращающихся частей, дисбаланс радиальных и торцевых биений, а также упругие колебания деформируемых элементов могут приводить к появлению периодически изменяющихся неуравновешенных сил высокой частоты (до 1000 Гц) и низкой амплитуды, которые через опоры

  передаются элементам корпуса судна. За весь период службы судна общее число циклов нагружения может достигать 10¹⁰—10¹² циклов;

• —    нерегулярный характер изменения условий плавания, выражающийся в локальном изменении степени нагруженности отдельных конструктивных элементов корпуса судна под действием внешних силовых факторов (ветер, волнение, ледовая нагрузка). В среднем подобное воздействие характеризуется низкой частотой (до 0,1 Гц) и высокой амплитудой нагружения. За весь период службы судна общее число циклов нагружения может достигать 10⁷—10⁸ циклов;

• —    активное воздействие перевозимых грузов на несущие элементы конструкций судов, выражающееся в механическом и химическом воздействии. Механическое воздействие приводит к появлению в последних динамических напряжений, имеющих различную амплитуду и частоту изменения (в зависимости от типа перевозимого груза). Химическое воздействие приводит к активации коррозионных процессов, а также проникновению в конструкционные материалы вредных примесей, ухудшающих их свойства.

Кроме того, действие вышеописанных источников нестационарных воздействий является во многом взаимосвязанным и нередко возникновение одного источника приводит к активизации другого. Методика исследования. Прогнозирование длительной прочности судовых конструкций, испытывающих циклическое нагружение, тесно связано с изучением вопросов механики зарождения и распространения усталостных трещин. На сегодняшний день известно множество разнообразных методик [1—4], позволяющих удовлетворительно прогнозировать динамику усталостного разрушения. Тем не менее вопросы зарождения и распространения малых поверхностных усталостных трещин (так называемых микрометровых трещин) исследованы недостаточно полно, несмотря на то, что именно на этот процесс приходится значительная доля (40—60 %, а для некоторых материалов 80—90 %) общей долговечности корпусных конструкций. Кроме того, малые трещины могут возникать на ранних стадиях циклического нагружения (приблизительно 10 % общей долговечности) и трудно регистрируются обычными методами контроля.

Прогнозирование начальной стадии усталостного разрушения сопряжено с рядом трудностей, наиболее существенной из которых является чрезвычайно сильное влияние микроструктуры материала на кинетику трещин. Для решения данной проблемы ранее была предложена математическая модель развития усталостных трещин на начальной стадии циклического нагружения (до появления макротрещины) [5, 6], в основе которой было кинетическое уравнение, отражающее превращение механической работы цикла нагружения в энергию упругой и пластической деформации металла в районе устья трещины.

Отличительной особенностью данной модели является присутствие в кинетическом уравнении нормирующей функции, учитывающей влияние микроструктуры материала на развитие усталостного разрушения и изменяющей свой вид в соответствии с экспериментально установленными закономерностями кинетики усталостных трещин dN = [ Ce ( De ) M + Cp (Dp )

M p

•^ ( a ) ,

где D e — мгновенное значение обратимой (упругой) составляющей внутренней энергии, идущей на развитие усталостной трещины в некоторой наиболее нагруженной области конструктивного элемента; D p — мгновенное значение необратимой (пластической) составляющей внутренней энергии; С и М — эмпирические коэффициенты, определяемые механическими свойствами материала конструктивного элемента, а также его напряженно-деформированным состоянием; ^( a ) — функция длины усталостной трещины, учитывающая нормирующее влияние микроструктуры материала на различных этапах развития разрушения.

Работоспособность полученной авторами модели была успешно подтверждена при циклическом испытании цилиндрических образцов, выполненных из бронзового сплава БрАЖН10-4-4 в условиях симметричного изгиба на испытательной машине МУИ-6000 при различных коэффициентах асимметрии цикла [6]. Однако дальнейшее развитие разработанной модели в целях ее использования для решения практических задач оценки длительной прочности судовых конструкций требует разработки соответствующей методической базы, основывающейся на современных численных методах. Общая структурная схема предлагаемой методики представлена на рисунке.

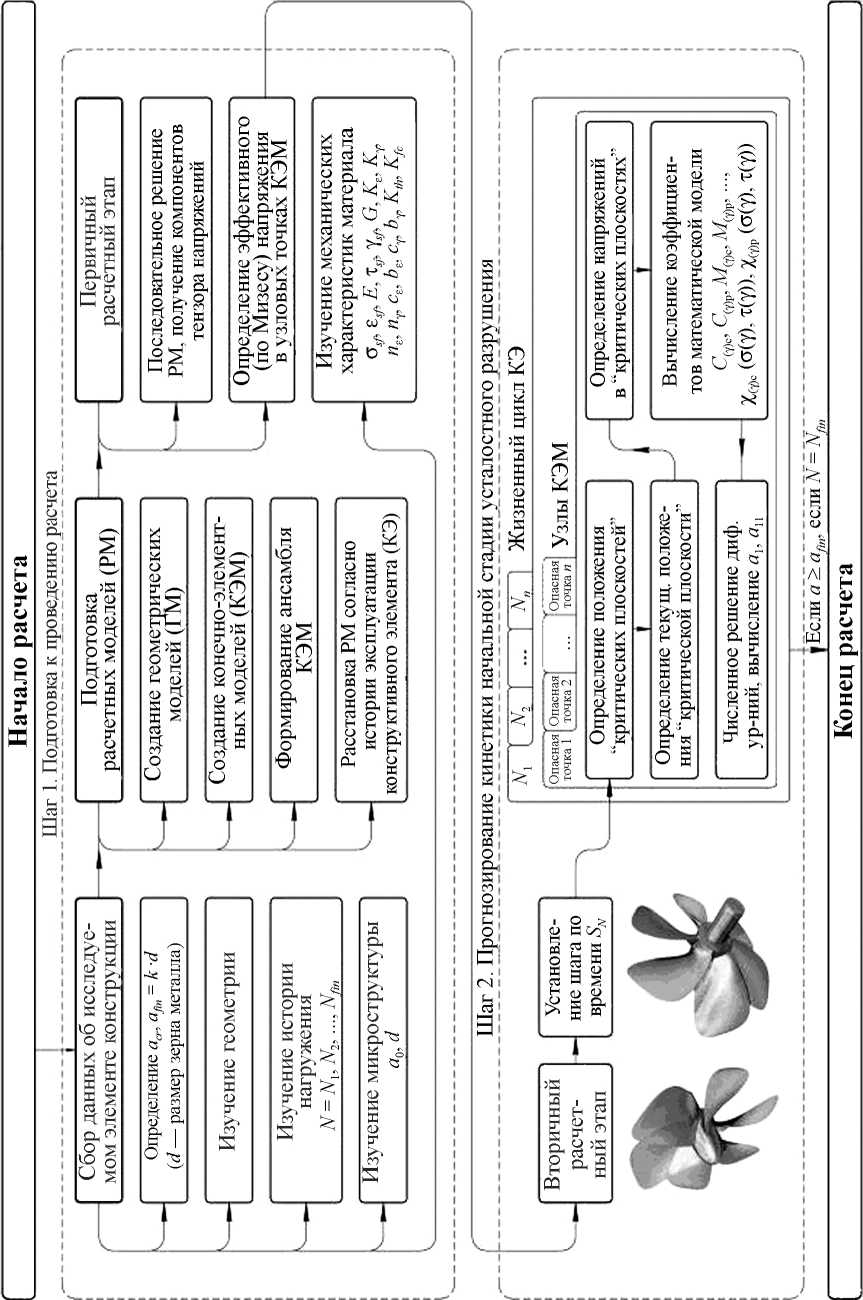
Методика прогнозирования длительной прочности судовых конструкций, испытывающих циклическую нагрузку

В соответствии с приведенной схемой процесс прогнозирования может быть условно разделен на три этапа.

• 1.    Подготовительный этап (сбор и классификация информации о конструкции).

  • 1.1.    Изучение геометрических особенностей конструкции, технологии ее изготовления и условий эксплуатации.

  • 1.2.    Изучение особенностей нагружения конструкции и разбиение ее истории эксплуатации N f на участки N 1 , N 2 , N 3 , N n с идентичными параметрами цикла нагружения и эксплуатационными условиями (наличие поверхностно-активных сред).

  • 1.3.    Экспериментальное исследование механических свойств и микроструктурных особенностей материала исследуемой конструкции с учетом выявленных ранее технологических и эксплуатационных особенностей, получение соответствующих коэффициентов модели.

  • 1.4.    Определение допустимого линейного размера усталостной трещины a fin .

• 2.    Предрасчетный этап (подготовка расчетных моделей для каждого участка истории эксплуатации конструкции).

  • 2.1.    Построение пространственной поверхностной геометрической модели.

  • 2.2.    Построение конечно-элементной модели путем дискретизации внутреннего пространства геометрической модели сеткой плоских расчетных элементов, соединенных между собой в узловых точках.

  • 2.3.    Построение ансамбля расчетных моделей посредством задания свойств материала, нагрузок и ограничений в узловых точках исходной конечно-элементной модели.

  • 2.4.    Расстановка расчетных моделей в последовательности, соответствующей динамике изменения внешних нагрузок.

• 3.    Первичный расчетный этап (численное исследование совокупности расчетных моделей методом конечных элементов [7]).

  • 3.1.    Решение пространственной упругопластической задачи для каждой из ранее созданных расчетных моделей и получение массива данных по динамике изменения мгновенного напряжения в узловых точках за один цикл нагружения [о_{( xx} ) (N)A n , [о₍ yyk NA n , [о₍ zzk NA n , [т < xyk NA n , [T ( zx ) ( N )A n , [T ( zy ) ( N )A n .

  • 3.2.    Определение динамики изменения мгновенного значения эквивалентного напряжения в узловых точках в соответствии с энергетическим критерием Р. Мизеса [8] (σ eqv ( N )) n :

• 3.3.    Выделение в объеме каждой из ранее созданных расчетных моделей «опасных» узловых точек: точек с наибольшим размахом эквивалентного напряжения, а также точек, в которых O ( a _{7 t})max ^ O cf . Создание массива данных по динамике изменения мгновенного напряжения в этих Точках ^[ О ( xx )^{( N )A}( dng)n , ^[ О ( yy )^{( N )A}( dng)n , ^[ ^ ( zz )^{( N )A}( dng)n , ^{[ t} ( xy )^{( N )A}( dng)n , ^{[ t} ( zx )^{( N )A}( dng ) n , ^{[ t} ( zy )^{( N )A}( dng ) n .

• 4.    Вторичный расчетный этап (применение математической модели).

  • 4.1.    Установление шага по времени для вычисления приращения усталостной трещины s N .

  • 4.2.    Начало цикла расчета.

    • 4.2.1.    Для текущей расчетной модели.

    • 4.2.2.    Для текущей «опасной» узловой точки:

      • а)    определение положения плоскостей развития усталостного разрушения в данной точке в соответствии с ранее определенной динамикой изменения мгновенного напряжения и выбранным шагом; б) определение динамики изменения значения мгновенного напряжения, действующего в плоскостях развития усталостного разрушения в данной точке [ t _(y)( N )A_{( dng ) n} , [σ ( ε ) ( N )] ( dng ) n ;

• 4.2.2.1.    Переход к следующей «опасной» узловой точке.

• 4.2.2.2.    Переход к следующей расчетной модели.

• 4.3.    В случае, если искомая величина a или контролируемая величина N превышают допустимые значения a fin и N f расчет немедленно прекращается.

• 5.    Окончание расчета .

° eqv = 72 • ⁽° -) ^- ° yy ) ) ^{2 + (}° yy ) ^- ° -)Г ^{+ (}° -) ^- ° -) ) ^{2 + 6 ( т}) ^+т(- ) ^{+ T} 2y ) ) .       ⁽²⁾

в) вычисление эмпирических коэффициентов математической модели С( т _(Y), о_(Е)), M ( t _(y), о_(е)),

D ( t ( _Y ) , 0 ( _E ) ); г) вычисление длины усталостной трещины а на данном расчетном шаге посредством численного решения дифференциального уравнения (1).

Конечным результатом применения вышеописанной методики является получение числа циклов нагружения N fin , при котором усталостная трещина достигнет допустимого значения a fin (граница применимости модели). Для определения числа циклов нагружения N rem , при котором усталостная трещина достигнет критического значения a cr (физическое разрушение) может быть использовано уравнение Пэриса [2] в виде:

N rem

„ (1 — B 2 ) a fin

—

п ( 1 — ^{В / 2} ) a _cr

C ( B) 2 — 1) - ( Y -Ao ) B’

где В — показатель степени для кинетической диаграммы усталостного разрушения; Y — поправочный коэффициент, учитывающий характер деформирования материала в устье трещины; A o — размах напряжения в данном цикле нагружения.

Для оценки остаточного ресурса конструкции может быть использована формула:

N = N_P +N -N                          (4)

fin rem cur , где Ncur — текущее число циклов нагружения.

Выводы. Обобщая изложенный материал, можно сказать, что одним из важнейших факторов обеспечения безопасности мореплавания является поддержание технического состояния корпуса судна на самом высоком уровне. В этой связи особую актуальность приобретает проблема разработки и усовершенствования существующих методик оценки и прогнозирования технического состояния судна с учетом его конструктивных особенностей и внешних эксплуатационных факторов. Развитие подобных методик позволит, с одной стороны, обеспечить минимальные затраты на техническое обслуживание и ремонт судов при соблюдении требований классификационных обществ, а с другой — прогнозировать и своевременно предупреждать разрушения корпусных конструкций.

Представленные методические аспекты отражают видение авторами обобщенного подхода к прогнозированию остаточного ресурса поврежденных судовых корпусных конструкций, работающих в условиях длительного воздействия циклических нагрузок. Широкое привлечение современных численных методов в рамках предлагаемого подхода позволяет визуализировать процесс прогнозирования, а также детально учесть геометрические особенности исследуемой конструкции и характер ее нагружения. Автоматизация процесса дает возможность в автономном режиме отслеживать деструктивные процессы, происходящие в корпусных конструкциях и концентрировать внимание команды на наиболее опасных участках.

Работа выполнена при финансовой поддержке РФФИ (проект № 10-08-00839-а).