Методические особенности решения задач по кинестатическому анализу рычажных механизмов

Кинетостатический анализ рычажных механизмов (кинетостатика) является одним из сложных разделов теории механизмов и машин и имеет своей целью определение реакций в кинематических парах для выполнения дальнейших расчетов на прочность. Для решения задачи обучения кинетостатике студентов при изучении дисциплины «Теория механизмов и машин» (ТММ) необходимо особое внимание уделять проектированию содержания этого раздела, особенно алгоритмизации выполнения такого анализа для кинематических цепей различного класса. Предлагаемая статья посвящена раскрытию этих вопросов на примере решения конкретной практико-ориентированной задачи.

В основном блоке [1; 6] содержания раздела приводятся общие сведения по кинетостатике. Следует отметить, что в основе кинетостатического анализа механизмов лежат два классических принципа общей механики [2; 4]: принцип Даламбера и принцип статической определимости. Применительно к механизмам принцип Даламбера формулируется следующим образом: если к звену, наряду с внешними силами, приложить силы инерции, и силы реакций в кинематических парах, то звено можно условно рассматривать находящимся в равновесии, и к нему применимы уравнения статики.

Принцип статической определимости заключается в равенстве количества неизвестных силовых параметров количеству возможных уравнений равновесия [5]. Для каждого звена плоской кинематической цепи можно составить три уравнения равновесия, следовательно, для всей цепи состоящей из n звеньев – 3n уравнений равновесия. В каждой кинематической паре 5-го класса при силовом расчете необходимо определить два параметра: для вращательной пары – величину и направление реакций; для поступательной пары – величину и точку приложения реакции. Для всей кинематической цепи общее количество неизвестных параметров будет равно 2р 5 . Условие статической определимости запишется как:

3n = 2P 5                                   (1)

Из уравнения (1) видим, что статически определимыми являются группы Асура [4], подвижность которых равна 0.

Учитывая вышеизложенное, составим алгоритм силового расчета механизма [4]: 1) вычерчивается в масштабе схема механизма в исследуемом положении; 2) определяются все внешние силы, приложенные к звеньям механизма, а также силы и моменты сил инерции; 3) проводится расчленение ведомой кинематической цепи на группы Асура; 4) расчет начинают с наиболее удаленной от ведущего звена группы, для чего ее изображают отдельно; 5) действие отсоединенных звеньев заменяют силами реакций; 6) в соответствующие точки звеньев прикладывают все действующие силы; 7) задачу обычно решают графоаналитическим методом, рассматривая равновесие группы находят искомые реакции, для чего составляются уравнения У F = 0; У M = 0. ; 8) на основании этих уравнений строится силовой многоугольник, (план сил), находятся реакции сначала во внешних кинематических, затем во внутренних. После этого переходят к следующей группе и так до тех пор, пока не будет произведен силовой расчет всех групп; 9) силовой расчет заканчивается исследованием ведущего звена.

Рассмотренных предпосылок достаточно, чтобы выполнить силовой расчет любого рычажного механизма.

В работах [3-5] показан рекомендуемый порядок кинетостатического расчета групп Ассура II класса 1-5 видов и группы III-го класса и ведущего звена.

Рассмотрим в рамках процессуального блока [6] кинетостатический расчет механизма на примере восьмизвенника, изображенного на рисунке 1.

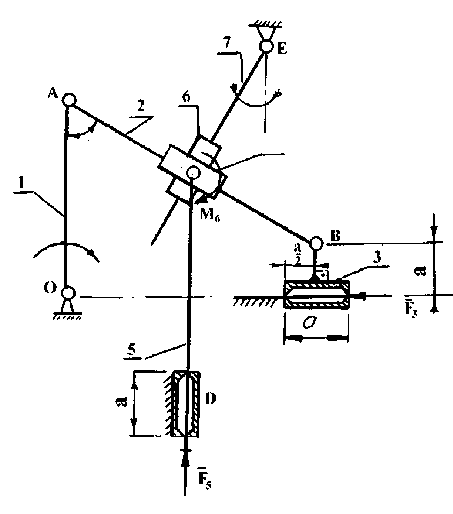
Требуется найти реакции

R12, R24, R05, R54, R03, R03, R67, R46, если известно: F 3 = 450H;

F5 = 300H; M6 = 60H • м;1сE = 0,4м;

1СД = 0,6 м; а = 0,2 м; АС = ВС ,l0A = 0,6 м

Рис.1. Схема механизма.

В соответствие с описанным выше алгоритмом выполним силовой анализ механизма.

• 1.    Выделим из состава механизма группу звеньев 6, 7 и нагрузим действующими нагрузками (см. рис.2).

  • 1.1.    Составим уравнение моментов относительно точки С для всей группы, надем реакцию R^t 07

Ж(С)₃ в 6,7 = 0      R 0₇ • ЕС- М б = 0

R^t 07 = М 6 /СЕ = 60 Н ^. м / 0,4 м = 150Н

• 1.2.    Составим векторное уравнение суммы всех сил , действующих на 7-е звено

X F(71 = 0 R07+Rn + R67 = 0

Строим силовой многоугольник.

R7 = 0; R =- R‘ =

Найдем                    ⁰⁷

= 150H;

• 1.3.    Рассмотрим равновесие 6-го звена и найдем,

• 2.    Рассмотрим расчет группы звеньев 4 – 5.

  • 2.1.    Составим уравнение векторной суммы всех сил, решим его графически

    

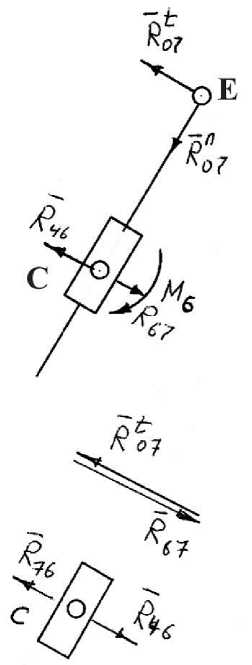
    Рис. 2. Расчет группы 7-6.

    
    

    2 F i25 = R 64 + R 24 + R 05 + R 05 + F 5 = 0

    
    
    

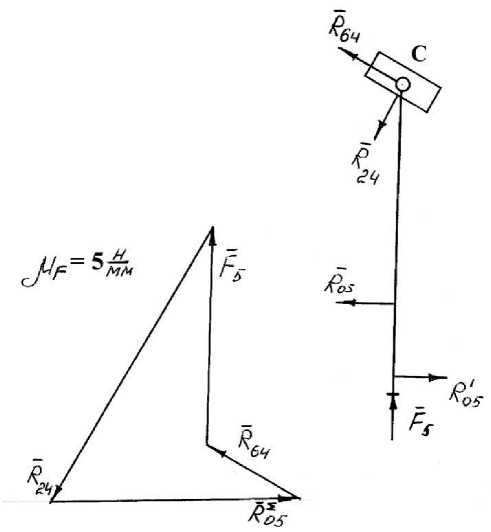
    Рис. 3. Расчет группы 5-4.

    
    

• 2.2.    Для нахождения реакций R 05 и R 05^' составим уравнение моментов относительно точки С для 5-го звена.

R46 =- R67 = R^

= 150H

Из плана сил найдем R 24 = 90 • 5 = 450H; R 05 + R 05 = 70 • 5 = 350H;

(СД + а)    , 0,6 + 0,2

R05 • СД = R„5 (СД + а)  R05 = С,         = ^5        = 1,33R0s

СД          0,6

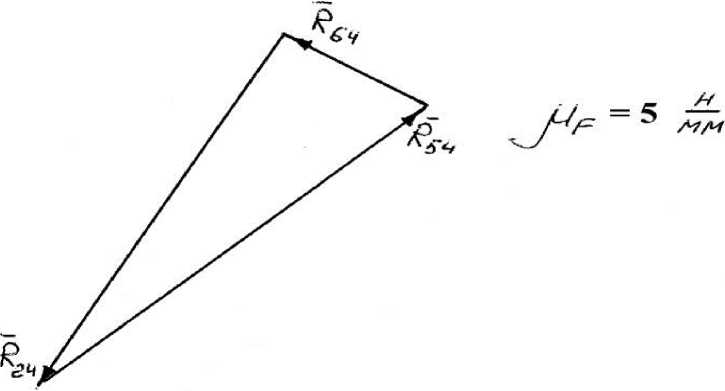
Рис. 4 Расчет точки С для 5-го звена

'

отсюда R05 = 1400H;  R05 = 1050H

2.3. Для нахождения реакции R 54 рассмотрим равновесие 4-го звена.

R54 = 90 • 5 = 450H

3. Группа звеньев 2-3.

3.1. Составляем уравнение моментов относительно точки В для 2-го звена:

ZM2зв(В) = 0 R42 • BC- R07 • 2BC = 0, отсюда

t

R12 = -R42 = 225H.

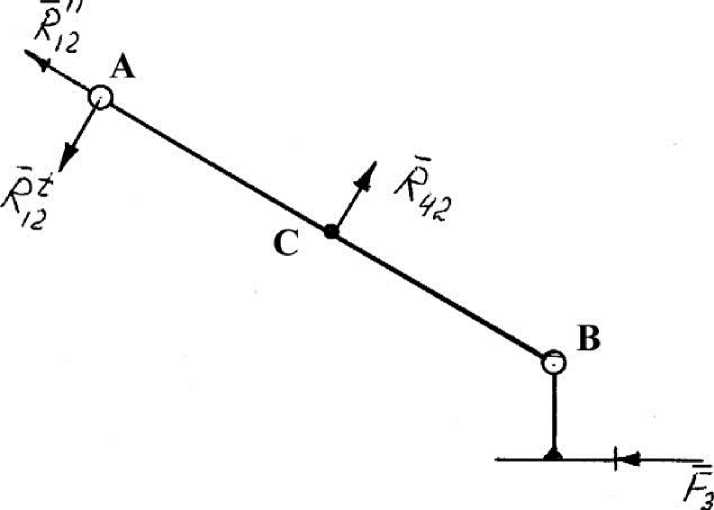
Рис. 5. Расчет группы 2-3.

3.2. Составляем векторное уравнение суммы всех сил, действующих на группу

Z F-з2’3 = 0

R 12 + R 12 + R 42 + F 3 + ( R 01 + R 01 ) = 0 , строим план сил

(см. рис. 6).

Из плана сил находим R 12 = 450H;

Rob + R03 )= 0

H

R F = 5 мм

3.3. Составим уравнение моментов относительно точки В для 3-го звена:

R 03 •

a     'a

—+ R03 • — = F • a

2        23

отсюда

—        '    —       .

R03 = R03 = F3 = 450H

Окончательно получим значения искомых реакций:

'

R07 = R67 = R46 = 150H;  R24 = 450H,  R05 = 150H;  R05 = 1050H;

'

R54 = 450H;  R12 = 450H; R03 =- R03 = 450H.

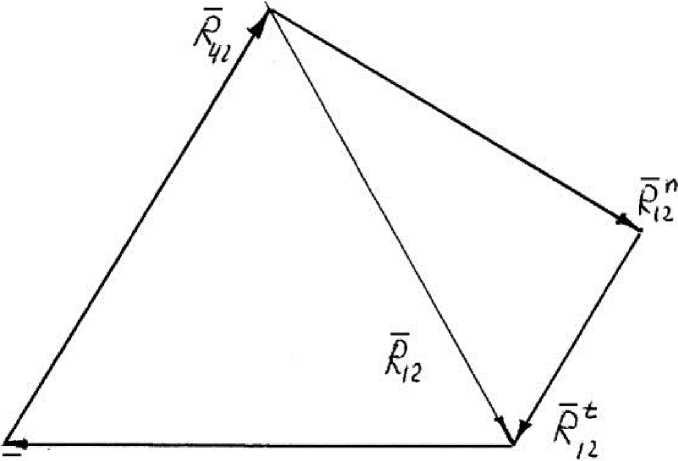
F3

Рис. 6. План сил группы 2-3.

Таким образом, представленное содержание кинетостатического анализа рычажных механизмов (теоретические сведения), описанный алгоритм этого анализа механизма с использованием имеющегося методического сопровождения обеспечивают эффективную самостоятельную работу студентов по решению задач силового расчета кинематических цепей различной сложности. На наш взгляд, данный подход формирует у студентов не только мотивацию к самостоятельному овладению знаниями по механике, но и способствует формированию инженерного мышления в целом.