Методические принципы проектирования космического аппарата на предельное энергообеспечение полезной нагрузки
Автор: Чеботарев В.Е., Фаткулин Р.Ф., Воронцова Е.О., Шангина Е.А., Баландина Т.Н.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Авиационная и ракетно-космическая техника
Статья в выпуске: 1 т.23, 2022 года.
Бесплатный доступ
Проектирование космического аппарата на начальных этапах осуществляется при наличии неопределенностей по параметрам и условиям. Определение проектных параметров происходит пошагово: определение номинальных значений проектных параметров, нормирование запасов ресурсов (масса, объем, энергопотребление) по проектным параметрам на парирование неопределенностей, проектирование космического аппарата на предельные ресурсы. Эксплуатация космического аппарата с включенной электрической нагрузкой содержит несколько этапов: выведение на целевую орбиту, ввод в штатную эксплуатацию, штатную эксплуатацию по целевому назначению, выведение из целевого использования при возникновении аварийных ситуаций. Система электропитания предназначена для обеспечения бесперебойного автономного электроснабжения бортовой аппаратуры во всех режимах и на всех этапах в течение срока активного существования космического аппарата с учетом наличия теневых участков орбиты от Земли и Луны. В данной статье разработаны методические принципы проектирования космического аппарата на предельное энергообеспечение полезной нагрузки при наличии неопределенностей по параметрам и условиям. Разработаны математические модели расчета параметров энергобаланса космического аппарата для различных вариантов реализации мощности сеансной нагрузки в зависимости от уровня освещенности орбиты и срока функционирования космического аппарата. Проведены оценки эффективности использования методических принципов проектирования космического аппарата на предельное энергообеспечение полезной нагрузки в зависимости от уровня освещенности орбиты и срока функционирования космического аппарата. Разработана методика нормирования запасов по энергоресурсам космического аппарата на парирование неопределенностей по параметрам и условиям, а также принципы ее применения при проектировании космического аппарата на предельное энергообеспечение полезной нагрузки.
Космический аппарат, полезная нагрузка, энергобаланс, теневые зоны орбиты, методика оценки эффективности
Короткий адрес: https://sciup.org/148324383
IDR: 148324383 | УДК: 629.783
Текст научной статьи Методические принципы проектирования космического аппарата на предельное энергообеспечение полезной нагрузки
Проектирование космического аппарата (КА) на начальных этапах осуществляется при наличии неопределенностей по параметрам и условиям. Поэтому определение проектных параметров КА в условиях неопределенности относится к классу стохастических задач и для упрощения ее решения и частичного сведения к детерминированной форме осуществляется пошагово [1; 3–6]:
– определение номинальных значений проектных параметров;
-
– нормирование запасов ресурсов (масса, объем, энергопотребление) по проектным параметрам на парирование неопределенностей;
– проектирование КА на предельные ресурсы.
В статье рассмотрены методические принципы проектирования КА на предельное энергообеспечение полезной нагрузки при решении задачи формирования требований к системе электропитания в условиях неопределенностей.
Обобщенные характеристики электрической нагрузки КА
Космические аппараты информационного обеспечения относятся к классу автоматических КА с автономным принципом функционирования в течение больших интервалов времени в процессе своего срока активного существования (САС) на орбите [1].
Эксплуатация КА с включенной электрической нагрузкой содержит несколько этапов: выведение на целевую орбиту, ввод в штатную эксплуатацию, штатную эксплуатацию по целевому назначению, выведение из целевого использования при возникновении аварийных ситуаций. Система электропитания (СЭП) предназначена для обеспечения бесперебойного автономного электроснабжения бортовой аппаратуры во всех режимах и на всех этапах в течение срока активного существования КА с учетом наличия теневых участков орбиты от Земли (ТУЗ) и Луны (ТУЛ) [1; 2].
Режимы работы КА по этапам различаются по распределению электрической нагрузки по времени: на начальных этапах режимы имеют переменную длительность и индивидуальную циклограмму энергопотребления, в то время как на этапе штатной эксплуатации режимы работы КА характеризуется определенной цикличностью, кратные периоду обращения КА ( Т КА ) или суткам. В общем виде циклограмму энергопотребления КА для каждого режима представляют в виде кусочно-непрерывной функции – последовательности переменных значений мощности нагрузки на интервалах заданной длительности в пределах выбранного цикла.
Для проектных оценок энергобаланса КА, как правило, используют обобщенные свойства циклограммы энергопотребления КА отдельного витка длительностью T КА : средняя по витку мощность нагрузки P н.ср , средняя по витку мощность дежурной нагрузки P н.д , средняя мощность сеансной нагрузки P с.т на теневом участке орбиты длительностью t т , средняя мощность сеансной нагрузки Р со на освещенном участке орбиты длительностью Т КА - 1 т [1]:
(
Р н.ср = Р с.т + 1 - I Р с.о + Р н.д . (1)
Т КА V Т КА )
Условия освещенности орбиты в течение года существенно изменяются в зависимости от положения Солнца относительно плоскости орбиты КА (угол ц с ): от максимально освещенной орбиты, на которой теневые участки отсутствуют, до максимально теневой орбиты, когда КА пересекает максимальные угловые размеры тени от Земли (ТУЗ).
Условие появления цикла теневых орбит в течение полугода имеет вид [1; 7; 9–11]
о <ц с <р max , sin в max = -З- , (2)
rКА где rКА – текущее значение величины радиуса орбиты; RЗ – средний радиус Земли (RЗ = 6371 км); в max - угловой радиус ТУЗ.
Закон изменения положения Солнца относительно плоскости орбиты КА в течение полугода для предельного случая (восходящий узел орбиты КА расположен в точке весны) определяется уравнением sin цс = sinис • sin(i -е), (3)
где i - наклонение орбиты; е - наклонение эклиптики; е = 23,45; ис — угловое положение Солнца относительно точки весны.
Длительность цикла теневых орбит определяется с помощью уравнения (3) из условия 0
<ц
с
sin и спр = sin e max / sin ( i -е ) . (4)
Для круговых орбит расчет относительной длительности ТУЗ проводится с помощью уравнения
КТ -
t туз 1
——=—arccos T KA П
' cos P max ' v cos П с ,
о
max
,
0
<
u
c
<
u
с.пр
,
где
T
КА – длительности витка;
t
туз – длительность ТУЗ.
Максимальное значение
К
Т
при
п
с
=
0 равно
K
туз
-
P
max
Т П Например, для круговых орбит КА системы ГЛОНАСС имеем [1; 8]
р
max
-
14,5 град,
К
ТУЗ
-
0,0806,
i
=
64,5 град,
ис
-
22,4 град.
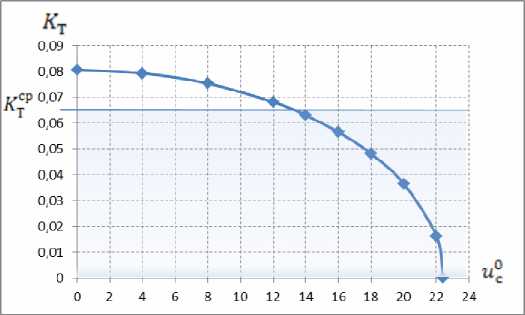
Зависимость
KТ
от
uс
приведена на рис. 1,
а
его среднее значение в зоне теневых орбит
0 < uc < испр составит КТР - 0,0636. В этом случае среднее значение КТ за цикл теневых и сол- нечных орбит определится из уравнения u
К ™
-
К
ср
•
2
•
р
-
0,0636--,—
-
0,0158.
Т Т
п
, 90
°
,
Рис. 1. Зависимость
KТ
от угла
uс
в зоне теневых орбит
Fig. 1. Dependence of
KТ
on the angle
uс
in the zone of shadow orbits
Проектные оценки энергобаланса КА Энергетические возможности СЭП, использующей в качестве генератора солнечные батареи (СБ), рассчитываются из условия удовлетворения потребностей электрической нагрузки КА на критичный случай: в штатном режиме, на конец срока функционирования КА (САС) и на теневых орбитах, с проверкой обеспечения положительного энергобаланса в каждом отдельном режиме на любом этапе [1; 2]. Критерием положительного энергобаланса является наличие запаса электроэнергии в аккумуляторной батарее (АБ) на любой момент рабочего режима, при условии, что в начале и конце цикла АБ полностью заряжена
W
mn
<
W
АБ
<
W
р.АБ
, (7)
где
W
min
– минимальное значение запаса электроэнергии в АБ;
W
АБ
– текущее значение энергоемкости АБ в процессе реализации данного режима КА;
W
р.АБ
– максимальное значение разрядной энергоемкости АБ.
Для определения проектных требований к мощности СБ и энергоемкости АБ оценивают энергобаланс КА при следующих допущениях:
– длительность цикла равна длительности витка
T
КА ;
– относительная длительность ТУЗ согласно формуле (5);
– возможность прохождения ТУЛ с относительной длительностью более
K
ТУЗ оценивается отдельно как экстремальное событие, аналогичное аварийным ситуациям;
– мощность СБ на освещенном участке орбиты постоянная и равна ее среднему значению
Р
СБ ср
;
– используется циклограмма штатного режима (1), мощность нагрузки представлена в виде составляющих: дежурной
P
н.д , постоянной по витку, сеансной (сверх дежурной)
P
c.о
и
P
c.т
.
Рассмотрим базовый вариант, когда сеансная нагрузка работает непрерывно по витку, включая и теневые участки от Земли (ТУЗ), с отличием по величине мощности. Для базовой логики работы рассчитаем энергобаланс КА в штатном режиме по методике [1] и определим требования к номинальному значению мощности СБ на конец САС при наличии ТУЗ: – энергобаланс W
(
1
-
К
т
Наб
•
Р
заб
=
Р
рАБ
-
К
т
^
,
(8)
T
КА
РзАБ
П
з.р
'
П
СБ
'
Р
СБ.т
Р
н.д
+
Р
с.о
Пн .
Р
р.АБ
=
н.д с.т ;
П
з.р
-П
н
– мощность СБ
Р
СБ.т
=
н.д с.о
П
СБ
' П
Н
А
т
K
Т
;
(1 - KТ ) ' ПЗР ' ПЗР ' ПАБ – энергоемкость АБ
P
+
P
W
ar
р
=
н.д с.т
-
K
т
-
Т
ка
,
П
з.р
•
П
н
WАБ.ном = Wmin+ WАБ.р, где Wmin – минимальное значение запаса электроэнергии в АБ; WАБ.р – разрядная энергоемкость АБ в процессе реализации данного режима КА; PСБ.т . – мощность СБ в конце САС на теневых орбитах; Pз.АБ – мощность заряда АБ; Pр.АБ – мощность разряда АБ; ηН , ηСБ , ηЗР – КПД преобразования мощности в блоках управления СЭП; ηАБ – КПД преобразования энергии в АБ. Для случая равномерного по витку потребления сеансной нагрузки (Pc.о = Pc.т = Pc) уравнение (9) для расчета мощности СБ на теневых орбитах примет следующий вид:
P
СБ.1
-н.д----с
-
(
1
+
А
т
)
.
П
н
-П
сб
На солнечной орбите KТ = 0, АТ = 0 поэтому возникает избыток генерируемой мощности СБ р „ , Р + Р
5
Р
сБ.т
=
^СБ.1
=
(
1
+
А
т
)
,
Р
сБ.о
=
н с
Р
СБ.о
П
СБ
-П
н
Вследствие деградации мощности СБ за САС (
t
САС ) ее начальное номинальное значению
P
С
0
Б должно быть увеличено
Р
СБ
=
Р
СБ.т
/exp
(-а
д
-
t
САС
)
,
(13)
где
а
д
- коэффициент деградации СБ.
Избыток генерируемой мощности СБ в начале САС составит
P
0
§
РСБсас
= / =
1/ exP
(
-а
д
-
t
САС
)
•
(14)
P
СБ.т
Например, для круговых орбит КА системы ГЛОНАСС имеем K туз = 0,08, Г: = 0,937, Паб = 0,9, получим Ат ® 0,11, 5РСБ т ~ 1,11.
При
а
д
-
t
САС
=
0,2
получим
5
Р
СБ.сас
~
1,22.
Анализ приведенных уравнений показывает, что в начальные периоды функционирования КА, а также на солнечных орбитах всегда образуются резервы энергетических ресурсов, обусловленных деградацией мощности СБ к концу САС и переменной длительностью ТУЗ на орбите КА [1].
Разработанная проектная модель расчета энергобаланса позволяет сформулировать требования к начальной мощности СБ
P
С
0
Б (формулы (9), (13)) и к номинальной разрядной энергии
W
АБ.ном
(формула (10)) при известных параметрах нагрузки и условиях освещенности орбит. При этом энергоемкость АБ задается для случая максимальной ТУЗ и в начале САС, при максимальной мощности потребления сеансной нагрузки в ТУЗ.
Эффективность применения адаптивной сеансной нагрузки Адаптивная сеансная нагрузка реализуется регулированием мощности ее потребления в течение САС, исходя из располагаемых энергетических возможностей СБ на теневых и солнечных орбитах, в начале и в конце срока функционирования.
Диапазон изменения мощности потребления сеансной нагрузки определяется по формулам (12), (13) для случая солнечной орбиты в начале САС (максимальное значение
P
п
м
н
акс
) и в конце САС (минимальное значение
P
п
м
н
ин
)
макс 0 Pc = Чсб Пн рсб рнд • мин
П
сб
-П
н
•
exP
(
-а
д
•
t
сас
)
'
р
сб
1
+
Ат
-Р н.д.
Текущее значение мощности потребления сеансной нагрузки
P
c
определяется по формулам (12)–(15):
P nA^reM «дЧфИСБ c = 1 + Ат
1
+
Ат
макс с----exP(-ад • tф )-Рн
Среднее значение мощности потребления сеансной нагрузки определяется интегрированием уравнения (16) в предположении постоянства среднего значения А
ср
:
Р
1
'
Т
Р
dt
(
P
-д
+
P
C”1 )
I
0
Р
,
1 - exP (-“
д
' t
cAc
)
ср tСАС i с 1 + Аср "' ’ 0 ад • tac ’ макс
Р
ср
=
р
с
5
Р
-.д
Pн.д max , Pс
А
ср
K ин Т (1 Kт ) • Пзр • Пзр • Паб Эффективность применения адаптивной сеансной нагрузки предлагается оценить с помощью относительного критерия
P
cp
I
0
'
(
1
+ 6
Р
н.д
)
-
(
1
+
А
ср H
P
H,
(
1
+
А
т
)
—•
.
РГ exp
(
-а
д
•
t
САС
)
.
(
1
+ 6
р.д
)
-
(
1
+
Ат
)
-6
р.д
1
+
А
ср
В варианте применения адаптивной сеансной нагрузки энергоемкость АБ задается для случая максимальной ТУЗ и в начале САС при максимальной мощности потребления сеансной нагрузки p + p макс
W
АБ.ном
—
W
mn
+
K
ТУЗ
'
Т
кА
.
П
з.р
•
П
н
Например, для круговых орбит КА системы ГЛОНАСС имеем [1; 8]: Ат ~ 0,11, при K™ — 0,0158 получим Аср «0,0138, при ад • tСАС = 0,2 получим 10 «0,9063, в результате, полагая Pн.д max Pс
0,5 получим
6
Рэа
~
1,4.
Полученные оценки подтверждают эффективность использования адаптивной сеансной нагрузки. Эффективность снижения мощности сеансной нагрузки на теневых участках орбиты Рассмотрим вариант оптимизации энергообеспечения КА за счет снижения мощности се-ансной нагрузки на теневых участках орбиты (в ТУЗ)
Р
т—
асн'
Р
,
Р
0—
Р
2, (20)
c.тснс c.о c.2
где
а
сн
-
коэффициент снижения мощности сеансной нагрузки в ТУЗ.
Для этого варианта мощность СБ на конец САС определяется по формуле (9):
Р
СБ.2
—
Р.д
+
Р
с.2
П
СБ
' П
Н
Р
л + ас •
Р
2
1 + ----сн—с.2 • а р + р , т
V
Р
н.д
+
Р
с.2
7
СБ.2
—
Р
СБ
'
exp
( а
д
'
t
САС
)
.
Полагая одинаковой мощность СБ на конец САС
Р
СБ
1
—
Р
СБ
2, оценим увеличение мощности сеансной нагрузки КА в этом варианте
6
Р
с
—
Рс^-
—
1
+
А
т
.
Р. 1 + агн • Ат сснт
Максимальное значение
6
Р
с
достигается при
а
сн
—
0
6
Р
м.сн
—
1
+
А
т
.
Полученное значение выигрыша по мощности сеансной нагрузки реализуется на теневых орбитах в конце САС (
t
САС ), когда происходит максимальная деградация мощности СБ.
Однако наличие избыточной мощности СБ в начальный период, когда срок функционирования КА tф меньше tСАС , позволяет обеспечить работу сеансной нагрузки с увеличенной мощ ностью Рс2 в ТУЗ до определенного времени функционирования (0 < tфт < tСАС)
Р
СБ.3
—
РСБ
•
exp
(
а
д
•
t
ф.т
)
Р
, +
Р
----н.д
-
(
1
+
Ат
)
.
П
н
•П
сб
Значение
P
С
0
Б определяется из уравнения (13), которое и подставляется в уравнение (24)
РСБ3 _ РСБ.2_____ exP (-ад • tф.т ) exP (-ад • tСАС ) ,
t
САС
-
t
ф.т
)^
д
=
ln
P
СБ.3
P
СБ.2
.
Уравнение (25) может быть преобразовано к виду
-t
^ _
1
1
in----
(
1
+ 5
Р
н-д-2
И1
+
А
т
)
----,
5
р
н.д.2
_
^
д
.
t
САС
а
д
'
t
САС
1
+ а
сн
'
А
т
+ (
1
+
А
т Г5
Р
н.д.2
P
c.2
С использованием уравнения (26) сформируем обобщенный коэффициент тени за цикл об Т
1
-
■
•
к
ин
.
к
t
САС
7
Таким образом, можно сделать вывод, что снижение мощности сеансной нагрузки на теневых участках орбиты только на заключительных этапах САС (
t
ф
т
<
t
САС
) позволяет увеличить мощность сеансной нагрузки (
5
Р
с2), что эквивалентно увеличению целевой эффективности. Однако в этом случае снижается коэффициент готовности КА в системной точке за счет увеличения времени выведения КА из целевого использования в течение цикла.
Рассмотрим предельный случай, когда в состав сеансной нагрузки входит полностью полезная нагрузка и при ее выключении включается компенсирующий обогрев по мощности, равный Р , = Р к.об асн с 22 J С.т .
Для оценки эффективности выключения полезной нагрузки в ТУЗ используем относительный критерий
5
Р
эт: произведение приращения эффективности и готовности КА
5
Р
эт
=5
Р
с
•
(
K
г
0
-A
K
)
>
1, (28)
где
K
г0
- нормированное значение коэффициент готовности КА в системной точке;
A
K
-
изменение коэффициента готовности КА.
В качестве показателя
A
K
возможно использовать один из показателей ТУЗ:
K
ТУЗ,
ин об
K
Т,
K
Т.
Подставляя в уравнение (28) значение
5
Р
с из уравнения (22) получим ограничение на коэффициент снижения мощности (
а
сн):
(
K
г
0
-A
K
)
-
(
1
+
Ат
)
-
1
0
< а
сн
<а
сн.пр
,
а
сн.пр
= 7
.
(29)
Ат В варианте выключения сеансной нагрузки в ТУЗ в конце САС энергоемкость АБ задается для случая максимальной ТУЗ и в начале САС, при максимальной мощности потребления се-ансной нагрузки в ТУЗ (19). Например, для круговых орбит КА системы ГЛОНАСС имеем [1; 8]:
Ат
~
0,11, при
t
САС
=
0,2
и
5
Р
нд2
~
0,5 получим
—^т- =
0,68 и соответственно
t
САС
K
Тоб
=
(1
-
0,68)
•
0,0158
=
0,005.
Полагая
K
0
=
0,995,
получим набор ограничений по а
сн
в зависимости от значений A
K
(табл. 1).
Зависимости показателей эффективности от
AK
AK
K
туз
=
0,08
к
Т
р
=
0,0636
к
Т
н
=
0,0158
к
Т
б
=
0,005
«
сн.пр
(при
5
Р
эт
>
1)
0,14
0,308
0,79
0,899
5
Р
эт
(при
а
сн.пр
=
0)
1,016
1,034
1,087
1,1
Как видно из таблицы, даже в наихудшем случае по теням выключение полезной нагрузки в ТУЗ дает положительный результирующий эффект при 0
< а
сн
<
0,14, а при
а
сн
=
0 значение
5
Р
эт
>
1,016 и
5
Р
м.сн
=
1,11.
Методика нормирования запасов по энергоресурсам КА Проектирование систем энергоснабжения КА на начальных этапах осуществляется при наличии неопределенностей по штатной программе работы КА, параметрам электрической нагрузки, условиям освещенности. Поэтому проектные параметры системы энергоснабжения КА (мощность СБ, энергоемкость АБ) определяются при расчете энергобаланса для наихудших условий: на конец срока активного существования КА и при максимальной длительности ТУЗ. Наличие неопределенностей в реализации энергетических параметров КА приводят к необходимости нормирования энергетических запасов по мощности электрической нагрузки, мощности СБ и энергоемкости АБ. Мощность электрической нагрузки КА в различных режимах формируется в виде суммы мощностей электрической нагрузки составных частей КА, на каждую из которых задаются ог- раничения в виде диапазона АР -Ар < р < Р + Ар, 5Р = —i-, iiii i Pi где Pi , Pi – фактические и номинальные значения энергопотребления i-х составных частей КА; APi - предельный диапазон отклонения энергопотребления от номинального значения i-х составных частей, задаваемые методом экспертных оценок, в пределах 5Pi = 0,05-0,15, в зависимости от новизны разрабатываемой аппаратуры. Энергопотребление КА как сумма случайных величин его составных частей с интервальным законом распределения при использовании принципа гарантированного результата формируется следующим образом (детерминированная модель) [1; 5]: n ~ ~
Р
КА
=
^
Pi
<
Р
н.КА
+ А
Р
д
,
i nn АР = УАР «УР-5Р «5Р- РнКА. дiii н.КА i=1 i=1 Однако в соответствии с центральной предельной теоремой, сумма случайных величин составных частей с интервальным законом может быть представлена как случайная величина с нормальным законом распределения вероятности (вероятностная модель) [1; 3–6] n ~ ~
Вер
[
Р
ка
<
Р
н.КА
+ А
Р
5
] =
Ф
Р
о
р
=
5
Р
р
Г"
-
Р
н.КА
,
n
Р
КА
=
^
Pi
,
i АРв = tP '° Р, где n – количество составных частей; tP – параметр распределения вероятности по энергопотреблению КА; оР - среднеквадратическое отклонение по энергопотреблению КА; ФР - интеграл вероятности (нормированная функция Лапласа), задаваемый в табличной форме [1; 3–6].
Для уровня вероятности, при котором гарантируется структурная устойчивость проекта (Ф
Р
«
0,997), значение параметра распределения вероятности
tP
«
2,8. Поэтому при составлении бюджета запасов ресурсов КА на парирование неопределенностей использование вероятностной модели снижает эти запасы в сравнении с детерминированной моделью [1]:
ΔP
в
=
P
≤
1, при
n
>
10.
ΔPд n,.
Для КА системы ГЛОНАСС
n
>
25,
ΔP поэтому в ≤ 0,56, а при δP = 0,05–0,15 получим ΔPд ЬР
δ
P
=
в
≈
0,56
⋅δ
P
=
0,03
-
0,08.
в
P
н.КА
Проектирование КА на предельное энергообеспечение полезной нагрузки
Проектирование КА на предельное энергообеспечение полезной нагрузки предполагает максимальное использование резервов энергетических ресурсов на повышение его эффективности.
Рассмотрен вариант использование адаптивной сеансной нагрузки путем регулирования мощности потребления полезной нагрузки (регулирование длительности сеансной работы) в зависимости от освещенности орбиты и срока функционирования КА. Использование адаптивной сеансной нагрузки повышает эффективность КА (для КА системы ГЛОНАСС можно получить
δ
P
эа
≈
1, 4).
Для того чтобы реализовать эту схему необходимо разработать соответствующую полезную нагрузку, комплекс автоматики и стабилизации СЭП на максимальные мощности от СБ и нагрузки на начальных сроках функционирования КА. При проектировании системы терморегулирования на максимальный режим «перегрев» следует учитывать, что средние за виток тепловыделения в этом режиме в начале и в конце САС будут различными. Однако в этой схеме не требуются запасы энергоресурсов на парирование неопределенностей.
Использование режима снижения мощности сеансной нагрузки на теневых участках орбиты позволяет повысить эффективность КА (для КА системы ГЛОНАСС можно получить
δ
P
эт = 1,016–1,11). В этом варианте можно не создавать запасы энергоресурсов на парирование неопределенностей (
δ
P
в
=
0,03
-
0,08), так как они могут быть скомпенсированы (при необходимости) снижением мощности сеансной нагрузки в ТУЗ.
Заключение
1. Разработаны методические принципы проектирования космического аппарата на предельное энергообеспечение полезной нагрузки при наличии неопределенностей по параметрам и условиям.
2. Разработаны математические модели расчета параметров энергобаланса КА для различных вариантов реализации мощности сеансной нагрузки в зависимости от уровня освещенности орбиты и срока функционирования КА.
3. Проведены оценки эффективности использования методических принципов проектирования КА на предельное энергообеспечение полезной нагрузки в зависимости от уровня освещенности орбиты и срока функционирования КА.
4. Разработана методика нормирования запасов по энергоресурсам КА на парирование неопределенностей по параметрам и условиям, а также принципы ее применения при проектировании космического аппарата на предельное энергообеспечение полезной нагрузки.
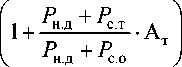
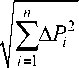
Список литературы Методические принципы проектирования космического аппарата на предельное энергообеспечение полезной нагрузки
- Чеботарев В. Е., Косенко В. Е. Основы проектирования космических аппаратов информационного обеспечения / Сиб. гос. аэрокосмич. ун-т. Красноярск, 2011. 488 с.
- Источники энергии систем электроснабжения космических аппаратов : монография / М. В. Лукьяненко, М. М. Лукьяненко, А. Н. Ловчиков, А. Б. Базилевский ; Сиб. гос. аэрокосмич. ун-т. Красноярск, 2008. 176 с.
- Вентцель Е. С. Исследование операций. Задачи, принципы, методология. 2-е изд., стер. М. : Наука, 1988. 208 с.
- Ильичев А. В., Волков В. Д., Грушинский В. А. Эффективность проектируемых элементов сложных систем. М. : Высш. шк., 1982. 280 с.
- Розанов Ю. А. Случайные процессы. М. : Наука, 1979. 184 с.
- Тараканов К. В., Овчаров Л. А., Тырышкин А. Н. Аналитические методы исследования систем. М. : Сов. радио, 1974. 240 с.
- Чернявский Г. М., Бартенев В. А. Орбиты спутников связи. М. : Связь, 1978. 240 с.
- ГЛОНАСС. Принципы построения и функционирования : под ред. А. И. Перова, В. Н. Хари-сова. 4-е изд., перераб. и доп. М. : Радиотехника, 2010. 800 с.
- Чеботарев В. Е., Воронцова Е. О. Методика обеспечения энергоресурсами окололунного спутника для прохождения теневых зон большой длительности // Космические аппараты и технологии. 2020. Т. 4, № 4. С. 233-240. Doi:10.26732/j.st.2020.4.06.
- Чеботарев В. Е., Воронцова Е. О., Сидорова Е. А. Моделирование теневых зон на окололунных орбитах и особенности расчета параметров систем электропитания и терморегулирования окололунного космического аппарата // Решетневские чтения : материалы XXIV Между-нар. науч.-практ. конф., посвящ. памяти генерального конструктора ракетно-космических систем академика М. Ф. Решетнева (10-13 нояб. 2020, г. Красноярск) : в 2 ч. Ч. 1. 2020. С. 49-51.
- Чеботарев В. Е., Воронцова Е. О. Методика расчета проектных параметров системы электропитания окололунного КА // Системный анализ, управление и навигация : материалы 25-й Междунар. конф. Евпатория, 2021. С. 150-152.
- Разработка систем космических аппаратов : под ред. П. Фортексью, Г. Суайнерда, Д. Старка ; пер. с англ. М. : Альпина Паблишер, 2015. 756 с.
- Туманов А. В., Зеленцов В. В., Щеглов Г. А. Основы компоновки бортового оборудования космических аппаратов : учеб. пособие. М. : Изд-во Моск. гос. техн. ун-та им. Н. Э. Баумана, 2010. 136 с.
- Эльясберг П. Е. Введение в теорию полета ИСЗ. 2-е изд. М. : Либроком, 2011. 544 с.
- Косенко В. Е., Звонарь В. Д., Чеботарев В. Е. Лунная информационно-навигационная обеспечивающая система // Актуальные вопросы проектирования АКА для фундаментальных и прикладных научных исследований. Химки, ФГУП «НПО имени С. А. Лавочкина», 2015. С. 323-329.


