Методический подход к оценке эффективности маскировочных средств

r

R 2 = (

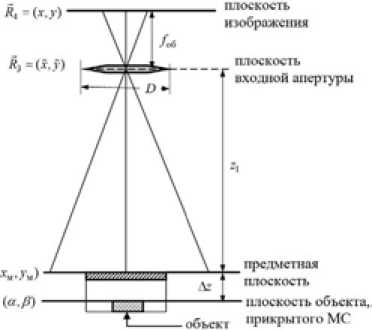
Рис. 1. Геометрия пассивной локации замаскированного объекта (ситуация, соответствующая гипотезе H ) ¹

Fig. 1. Passive ranging geometry of camouflaged object (situation according to hypothesis H ₁)

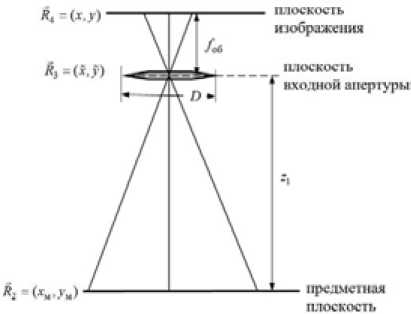
Рис. 2. Геометрия пассивной локации (ситуация, соответствующая гипотезе H 0 )

Fig. 2. Passive ranging geometry (situation according to hypothesis H ₀)

реноса изображения из рассматриваемой плоскости в фокальную (плоскость изображения) ИК-системы разведки.

С учетом изложенного рассмотрим задачу определения амплитудного распределения в плоскости изображения, соответствующего гипотезе H ₁. На рис. 1 представлена геометрия пассивной локации замаскированного объекта с необходимыми обозначениями. Условия пассивной локации, соответствующие гипотезе H 0 , представлены с необходимыми обозначениями на рис. ^2.

Предположим, что амплитудное распределение излучения объекта задано и описывается функцией U0(α, β). Амплитудную функцию размытия маскировочного средства обозначим через F1(xм, yм, α, β). Тогда амплитудное распределение на внешней поверхности маскировочного средства будет иметь вид и2 (хм, Ум) = JJ Uо (а, в)Fi (хм, Ум, а, в)dxdp = JJ Uо (Rx)Fi (Rt , Rx, ^z)d2Ri • (1) Sоб                                           Sоб

Интегрирование в данном случае ведется по поверхности объекта, подлежащего маскировке. Кроме того, будем полагать, что маскировочное средство обладает собственным излучением, так что амплитудное распределение на внешней поверхности маскировочного средства представляется в виде

U ₂ ( х _м, y _м) = U ₂ ′ ( х _м, y _м) +Δ U ₂ ( х _м, y _м) ,                                       (2)

где Δ U 2 ( x м , y м ) – амплитудное распределение на внешней поверхности маскировочного средства, вызванное собственным распределением.

Амплитудное распределение подстилающей поверхности может носить любой характер в зависимости от температурных и атмосферных условий, растительности, состава почвы, времени года. Обозначим амплитудное распределение подстилающей поверхности через – 265 –

U 2 _пп ( х м , У м ), где координаты х _м, У _м находятся вне внешней поверхности маскирующего средства. Следовательно, в предметной плоскости амплитудное распределение представляет собой сумму распределений, имеющей различную природу образования:

^U 2 Е ⁽ х м , y м ) - U ^{2 ( х} м , y м ) + A U ₂( ^х м , y м ) + U ^{2 ( х} м , y м ) -= U ₂( х м , У м ) + U _2пп ( х м , У м )

Амплитудное распределение для гипотезы H , в плоскости изображения находится (в случае невозмущенной среды распространения) на основе интегрирования по соответствующим источникам:

S м

⁺ Jf U 2пп ⁽ х М м , y м ) F 24 ( x, У, х М м , y м ) dx м dy м ,

ПП2

в выражении (4)

1    j П ( x М + у М ) ₁    j n ( x ² + у ² )

F _1A (x , у , x м , у м ) =      e             .e ^- f¹

^ z \             ^- f об

^x рс^{( x} , ^y ) e

^- j П [ ( x -t- M Г м ) ^{x +}( y + My м ) ^y ] J об

dxdy,

ОТ где x, y - координаты во входной плоскости формирующей оптики (рис. 1 и 2); M = f об /z1; X - средняя длина оптической волны; PC (х,y) — (функция зрачка объектива.

В первом слагаемом интегрирование ведется по внешней поверхности маскировочного средства, а во втором - по поверхности подстилающей поверхности, исключая внешнюю поверхность маскировочного средства, и в пределах поверхности, ограниченной полем зрения средства ИК-разведки.

Л-Г

При известном амплитудном распределении U ( x , у ) распределение интенсивности устанавливается путем усреднения произведения комплексно-сопряженных значений и ( x , у ) [7]

I ! ( X , у , t ) = U ( X , у , t ) . U * ( X , у , t )) .                                                    (6)

В этом случае амплитудное распределение в плоскости изображения и0(Г, У) = JJ U 2пп (Гм, Ум ) F„( Г, у, хм, ум ) dxм dy м.                         (7)

⁵ "3

Интегрирование выполняется по всей поверхности, ограниченной полем зрения разведывательного ИК-приемника.

Распределение интенсивности в плоскости изображения, обусловленной излучением подстилающей поверхности, находящейся в поле зрения разведывательного ИК-приемника, определим аналогично предыдущему случаю:

I о ( х , y , t ) = Uj о( х , y , t ) . и * ( х , y , t )\                                             (8)

Если учесть фоновое излучение и внутренние шумы приемника (пересчитанные на вход в виде добавки к фоновому излучению), то можно каждой гипотезе, подлежащей различению, поставить в соответствие аддитивные смеси:

н 1 : £ ( x, y, t ) = 1 1 ( x, y, t ) + n \ ( x, y, t );

H о : A x , y, t ) = I о⁽ x , y, t ) + n о⁽ x , y, t ).

Определим «за противника» оптимальный алгоритм обработки входного воздействия, обеспечивающего наилучшим образом (в смысле минимального значения суммарной ошибки) определение, что в принимаемой смеси 5 ( x , У, t ) содержится сигнал 1 [ ( x , у , t ) или сигнал 1 ₀( x , у, t ). При этом гипотезы составляют полную группу событий, так что сумма вероятностей P ⁽ Н ^ ■ P ⁽ Н ° ) = 1.

Размеры элемента матричного ИК-приемника удовлетворяют условию 2

AS = (xi - xi-) • (yj - y j-) = Ax - Ay = Aj - A! = Aj , где AS - чувствительная площадь поверхности элемента приемника. Величину сигнала (тока), снимаемого с элемента, имеющего коорди-,, наты (Xi, у), можно определить с помощью выражения xi yj

^' = nV J j « x,y)dxdy, ,                                  О⁰)

i 1 y j 1

где e – заряд электрона; h – постоянная Планка; ν – средняя частота оптических колебаний.

Применительно к сигналу от замаскированного объекта можем записать: ^x i ^y j

А( i, j ) = V J f ⁵ i^{( x},^y, t ) ^dxdy .                                          ⁽¹¹⁾

x i -Д 1 y j -Д 1

Шум, обусловленный фоновым излучением и, возможно, излучением постановщика помех, прикрывающего объект, описывается выражением xi yj

«1 ( i , j ) = n e j j ” t ( ^ , y ) dxdy .                                              (1²)

x i -д , y j -A .

Аналогичными выражениями можно описать и сигнал от подстилающей поверхности. Следовательно, мы можем записать:

^H 1^_v,^j = ⁿ_lv,_n ⁺ _Mv, = j I_v

H0 ■ ^(i, j) n0 (i, j) + IO (i, j) nOij + IOij где i = 1^m; j = 1^ l; m x l - размеры матрицы ИК-приемника.

В рассматриваемом случае распределение внутренних шумов приемника является, как правило, нормальным. В соответствии с [8] плотность вероятности шума можно записать как lm        - ij

® k _х m (---, n j ,-^ = ПП e 2'^                              (14)

i=1 j=i где ^Ш - средний квадрат (дисперсия) флуктуаций шума; n2 - квадрат значения шумов на выходе ij-го элемента приемника за время отсчета.

Поэтому многомерные условные плотности распределения изображений на выходе приемника, соответствующие гипотезам H ₁ и H ₀ в предположении о статистической независимости значений сигналов и помех в элементах матрицы приемников, будут иметь вид

( & j — I 1ij — n ij ) ²

о ( /Я^ГТГГ 1 e   25Ш ■(15)

k•■ UA-•     1 1nn                    ;

l m              - « j I 0 j ^- n 0 ij ) ²

»k ™  ^Hо) = ПП  '*   2'ш   , i=1

где I_Uj и I_Oy - значения токов в элементе матрицы приемника от замаскированного объекта и ПП соответственно.

Применительно к задаче различения сигналов в данной ситуации наиболее приемлем критерий идеального наблюдателя [9]. Определим алгоритм принятия решения:

^^ (..., ^.,.../H ) ® к х m (..., ^ i.,..J H 0 )"

,           ( ^ j - 1 0 ij - n 0 ij )2 - ( ^ ij - 1 1 ij - n i ij )2 P ( H ) l m jjjjj = 1ГТйП Г] [ П e       25 ш        = P ( H q ) . pr 0 i = 1 j = 1                                                       (17)

P pr _{( Н 1} )    1 i £< ^ - _У n 0 ij )² -^ - i j -_ч j )²

P.(Hо)e где Ppr(H1) и Ppr(H0) - априорные вероятности.

Преобразуя выражения и логарифмируя обе части, получим t £.Ы,^j) > ,2bPrHl + f £(I + nj)2 -(I«j + noj'2 , (18) где M = I - I          n  - n              РГ         ='

ij        ijj       Oij ’ i ,j        1 i,.j0

В соответствии с [9]

l ml m

¹⁽ )    ■? = ?^ ^ = 1^{( Xij 1ij} ) ’ ^o( ) S^ j = r^{( 0 ij 0 ij} )

Учитывая, что априорные вероятности получения сигналов от истинной и ложной целей равны, алгоритм принятия решения примет следующий вид:

• H > q1 =i\]=\j ij    jHо <

Ej™)

= h .

Структурная схема оптимального приемника, реализующего алгоритм (3.36), представлена на рис. 3.

Проведем анализ алгоритма, изображенного на рис. 3. Как видно из выражения (9), величина q ₁ представляет собой сумму большого числа случайных величин и в соответствии с центральной предельной теоремой ее закон распределения может быть признан нормальным. Поэтому для определения вероятности суммарной ошибки P c ( q ₁ ) достаточно найти математи- – 268 –

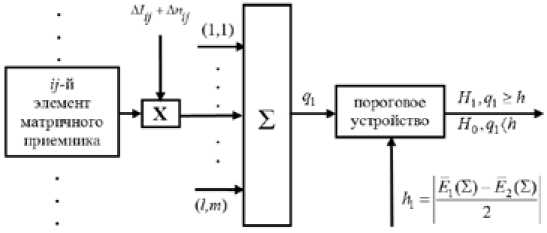
Рис. 3. Структурная схема оптимального приемника при различении двух изображений

Fig. 3. Optimal receiver structural schematics with the differences of two images

ческое ожидание и дисперсии плотности вероятности распределения q 1 при условии справедливости гипотез H 1 и H„

■, и дис-

Если справедлива гипотеза H , то ^ = I_Ai + n_Ai ,•, и математическое ожидание ( q ,( )) j j j                                                       11

персия ^ 2 1 ( у i ) будут определяться следующими выражениями:

ст2 ■

^■■I 1 )

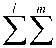
i = 1 j = 1

( / 1 ij + П 1 ij )( b i j ₊A n j );

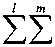
:I , + n , )(1 - ( A I j + A n , ) ] ’ .

i = 1 j = 1

Аналогично для гипотезы H , :

lm

(,1(Ц = ££ ( I.j + „ ,W, + A ^

i i j i lm ст 2

^q1 ( I 0 )

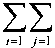
0 j ₊ n 0 j ^{)(1 -} (M j + ^A n j ) J .

lm

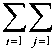
Тогда плотности вероятности распределения величины q 1 будут описываться выражениями:

( q i - q q i ( IiV 2 a ²

W ^ ( qj H i ) = _----- e     q1 ⁽ I 1)   ;

^{V 2} ^^a q i ( I 1 )

W ^ ⁽ qj H o ) = ^=---- e ^{V2 na} q i ( I 0 )

( q ,^-( q , ⁽ Io)p

2a- q ( I )

.

Вероятность суммарной ошибки с учетом выбранного критерия и выражений (24) можно определить с помощью выражения

P c ( q , ) = P pr ( H 1 ) P ( H 0 / H 1 ) + P pr ( H o ) P ( H 1 / H o ) =

f r                      ^

= 2 ^{( P} ( H ^{0 /} H , ) + P ( H * / H _o) ) = 2и W . ( q , / H 2 ) ^dq , + j W . ( q , / H o ) d- q ,

—с

h

где P„r ( H i ) = P„r ( H о ) = 0,5 - априорные вероятности появления в поле зрения замаскирован- pr 1 pr 0 _*

ного объекта и лишь ПП; P ( H ₀/ H ₁) – вероятность принятия замаскированного объекта за ПП;

P ( H ^* / H ) – вероятность принятия ПП за замаскированный объект.

Вероятности перепутывания будут определяться выражением

« h

Р ПеР J W е ( qH о ) dq i ; p. = J W е ( q i / н i ) dq i . (26) h -

Полученные таким образом вероятности перепутывания позволяют оценить эффективность средства маскировки и кроме этого, что весьма важно, обеспечивают построение модели процесса поиска замаскированного объекта в условиях преднамеренных помех.

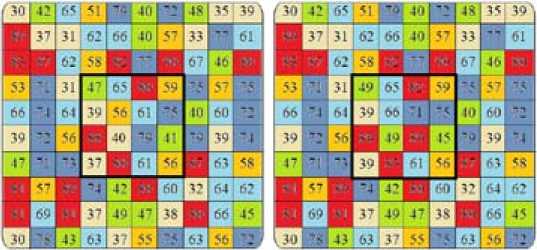
Для исследования зависимости вероятностей P c , P пе¹⁾ и P пе²⁾ от значений сигналов и шумов было проведено математическое моделирование на ПЭВМ в среде Matcad. Пример распределения интенсивностей по поверхностям изображений подстилающей поверхности и замаскированного объекта приведен на рис. 4.

В качестве тестового изображения задано изображение квадрата размерностью 10х10 элементов с неоднородной интенсивностью излучения (среднее значение интенсивности 55-60). Каждый элемент изображения соответствует элементу матрицы фотоприемника с соответствующими этому элементу значениями токов, возникающих в матрице приемника. В центре изображения задавался тестовый замаскированный объект в виде квадрата размерностью 4х4 элемента, имеющий увеличенную интенсивность.

Для оценки вероятности суммарной ошибки от степени подобия изображений в изображении замаскированного объекта изменялись значения элементов ( К элементов имели интенсивность большую, чем в изображении подстилающей поверхности, на 10-90 %), при этом уровень шумов был одинаковым.

На рис. 5 представлены графики зависимости вероятности суммарной ошибки от степени подобия изображений.

Из анализа полученных зависимостей можно сделать следующие выводы. При равных значениях шумов (в нашем случае n ₁ = n ₂ = 10) в изображениях замаскированного объекта и

H 1                                   H 0

Рис. 4. Пример распределения интенсивностей на изображениях замаскированного объекта и подстилающей поверхности

Fig. 4. Example of intensity pattern on camouflaged object’ and underlying surface images

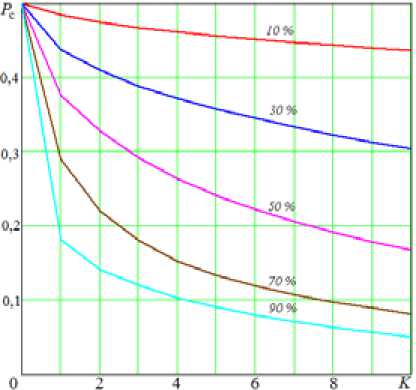
Рис. 5. Зависимости P c от степени подобия изображений

Fig. 5. Pc dependencies on images degree подстилающей поверхности различие в уровнях сигнала в 5-10 % не оказывает существенного влияния на вероятностные показатели различения. Для достижения максимальных значений вероятности суммарной ошибки и перепутывания при прикрытии объектов маскировочными средствами будет эффективным применение активных маскирующих помех, подобранных по мощности, при этом уровень необходимой мощности помехи не слишком отличается (на единицы процентов) от уровня мощности сигнала.

Таким образом, с использованием метода интегрирования по источнику получено амплитудное распределение излучения, исходящего от прикрываемого объекта, по внешней поверхности маскирующего средства. Путем его вложения в суммарное распределение общей площади, ограниченной полем зрения разведывательного ИК-приемника, можно оценить составное распределение в предметной плоскости с дальнейшим переносом изображения из рассматриваемой плоскости в фокальную плоскость системы разведки. Это позволило разработать методический подход к оценке эффективности маскирующих средств, позволяющий достаточно строго учитывать распределения интенсивностей излучения по поверхностям объекта и подстилающей поверхности.