Методический подход к оценке количества необнаруженных дефектов естественной семантики программы с требуемой степенью доверия при верификации программного обеспечения бортовых цифровых вычислительных комплексов космических аппаратов

Постоянное повышение требований к разрабатываемым бортовым цифровым вычислительным комплексам космических аппаратов (БЦВС КА) вызвало рост сложности и размера программного обеспечения (ПО) как наиболее гибкого компонента, расширяющего функциональные возможности КА. Данный факт обусловил значительное увеличение трудозатрат на разработку ПО БЦВС КА как в абсолютном значении, так и в сравнении с трудозатратами на создание

технических средств. По некоторым оценкам, 15 % от общего количества затрат отводится на верификацию ПО, при этом наблюдается тенденция к увеличению этой доли. В условиях секвестра бюджета из-за сложной внешнеэкономической ситуации вокруг России важным является использование таких методов разработки ПО, в том числе методов верификации, которые позволяют экономить государственные средства [1, 2].

Основной путь снижения затрат на верификацию ПО – максимальная автоматизация процесса исследования программных продуктов.

Том 2

Методом верификации, имеющим наибольшую степень автоматизации, служит статический анализ (СА). Главный недостаток СА – ограниченное множество типов обнаруживаемых дефектов ПО, расширение которого является основным направлением развития данной группы методов верификации ПО [3–5].

Для снижения трудозатрат на верификацию ПО предложен подход, основанный на СА программ на предмет обнаружения дефектов естественной семантики (ДЕС). Естественная семантика представляет собой размерность физических величин, интерпретируемых в идентификаторах исходного кода (ИК) программы. Для реализации контроля отсутствия ДЕС необходимо выполнить отображение множества идентификаторов на множество векторов, описывающих размерность, а также отобразить операции с идентификаторами на операции с векторами. Далее производятся вычисления с векторами в порядке, описываемом абстрактным синтаксическим деревом с контролем условий корректности.

Структура метода верификации ПО основывается на задачах, стоящих перед данным интегральным процессом разработки. Наравне с обнаружением и регистрацией программных дефектов в рамках верификации ПО встроенных систем необходимо доказать устранение дефектов с высокой степенью доверия, под которым предлагается понимать конкретные значения доверительного интервала I _β ^ТРЕБ и доверительной вероятности β ТРЕБ [6–8].

Для доказательства устранения дефектов ПО воспользуемся величиной, характеризующей количество необнаруженных дефектов:

N НЕОБЩ = N ОБЩ ^- N ЭБН , (1)

где N О _Б щ - количество «собственных» дефектов программы до проведения верификации ПО; N _ОБН – количество обнаруженных «собственных» дефектов программы.

На практике для оценки количества дефектов до начала верификации N _ОБЩ применяются различные модели надежности: эвристическая, Джелински-Моранды, Миллса.

Простая эвристическая модель и модель Джелински-Моранды не могут применяться для оценки количества ДЕС, так как идеи, лежащие в их основе, противоречат сути СА, позволяющего по некоторой математической модели обнаруживать все возможные дефекты за один проход анализатора независимо от того, каким специалистом осуществляется исследование. При этом если рассматривать СА как контрольный пример в рамках тестирования, то интенсивность появления дефектов после его выполнения снизится сразу до нуля,

что не позволит анализировать временные интервалы между проявлениями дефектов [9, 10].

Учесть вероятностный характер выявления ДЕС в оценке их количества до начала верификации, обусловленный характеристиками ИК программы и неизвестным законом распределения дефектов по составляющим выражений кода, возможно с использованием статистических моделей надежности, основанных на преднамеренном внесении дефектов в ПО. К классу подобных моделей относится модель Миллса, в которой вероятности обнаружения «собственных» дефектов и преднамеренно внесенных считают равными, а выражение для количества дефектов в программе до начала испытаний, исходя из принципа максимального правдоподобия, имеет вид [10]

^N ОБЩ =

N ^ПР

N ОБЩ N ОБН

N ^ПР    ’

N ОБН

ПР где NОБщ - количество преднамеренно внесенных дефектов в программу; NПБН — количество обнаруженных дефектов программы из числа

преднамеренно внесенных.

В модели надежности Миллса преднамеренное внесение дефектов производится до начала испытаний, что не может быть применено для оценки количества ДЕС в ПО, так как при этом существует вероятность взаимной компенсации с «собственными» дефектами программы. Свести риск подобной компенсации до нуля невозможно, однако минимальных значений для конкретного варианта ИК программы он достигнет при внесении дефектов после выявления «собственных». При этом N _ОБН определяется методикой СА для поиска ДЕС программы и зависит от характеристик ИК программы, N ОБЩ обусловливается количеством операторов программы, содержащих операции с естественной семантикой, N ПБ_Н в случае многократного проведения опытов будет иметь различные значения, что объясняется случайным попаданием преднамеренно вносимого ДЕС в одну из составляющих оператора (операцию или операнд). Закон распределения N О^Н неизвестен, поэтому в соотношении (2) предлагается исполь-

зовать оценку математического ожидания (МОЖ) данной величины М N О^ПБ _Н :

^/

^N ОБЩ =

N общ N ОБН M [ N ОБН ]

•

Конечное выражение для количества необ-

наруженных дефектов получается путем замены в

выражении (1) N _ОБЩ на соотношение (3):

^N НЕОБН

= ^N ОБН

ПР

N ОБЩ

( M [ N о^ПБн ]

- 1

J

Слабым местом моделей надежности, основанных на внесении дефектов, является процедура преднамеренного внесения, поскольку предполагается, что вероятности обнаружения «собственных» и преднамеренно внесённых дефектов равны [9]. Данная проблема возникает вследствие высокой сложности учета индивидуальных особенностей программистов (стиль, квалификация и т.п.) при выполнении прогноза возможной локализации «собственных» дефектов, который может быть использован в качестве множества потенциальных точек для искажения. Помимо своеобразия программистов необходимо уделять внимание и специфике характеристик ИК программы (для ДЕС это частота появления операндов), что является вполне формализуемой задачей.

Процесс внесения ДЭС предлагается рассматривать на представлении программы в виде мультимножества [11]:

SW = { stmt I stmt е STMT }, i = 1, I ,        (5)

где stmt i e STMT - i -й оператор программы, принадлежащий множеству операторов программы STMT .

Если абстрагироваться от синтаксиса конкретного языка программирования (ЯП), то любой оператор из (5), указывающий ЭВМ на выполнение вычисления, является некоторой комбинацией множества операндов, представленных идентификаторами ИК программы, и операций, определенных в спецификации ЯП:

stmti=( OpRA, opr", opr", OPMNDi^ (6) где OPR А = {opr A opr Ae OPR A, j = 1, J} i                 ij             ij                 А мультимножество арифметических операций i-го оператора, порождаемое множеством арифметических операций ЯП OPRA; J = OPRA^ — величина, характеризующая количество арифметических операций i-го оператора; opr^ е OPR П - операция присваивания i-го оператора, принадлежащая множеству операций присваивания ЯП; oprС е OPR С -операция сравнения i-го оператора, принадлежащая множеству операций сравнения ЯП; OPRNDi = {oprndil | oprndil е OPRND, l = 1, L} -мультимножество операндов i-го оператора, порождаемое множеством операндов программы OPRND; L = jOPPWDj - величина, характеризующая количество операндов i-го оператора.

Различные варианты структуры оператора программы, используемые для внесения ДЕС, описываются на основе выражения (6):

stmt i = ( OPR A , opr П , 0 , OPRND i ) - оператор, содержащий арифметические операции и операцию присваивания;

stmt i = ( 0 , opr ⁿ, 0 , OPRND i ) - оператор, содержащий операцию присваивания;

stmt i = ( 0 , 0 , opr i^C , OPRND i ) - оператор, содержащий операцию сравнения.

Характеристиками ИК программы, оказывающими влияние на эффективность поиска ДЕС, являются частоты появления операндов, имеющих одинаковые семантики. Очевидно, что чем больше переменных одной семантики в программе, тем выше должна быть вероятность их появления в качестве искажающего воздействия. Реализация данной закономерности осуществляется на мультимножестве, состоящем из Q вхождений операндов в программу и порождаемом множеством уникальных операндов:

OPRNDBX =     _

• =    ^{ oprnd q | oprnd q ^{е OPRND} , q = 1, Q ^}.    ⁽⁷⁾

Для выполнения выбора элемента set из множества SET по закону равномерной плотности распределения используется функция rnd : SET ^ set . Реализация функции следующая:

-1

rnd ( SET ) = set , при Р _выб ( set ) = ( SET ) . (8)

Применяя функцию (8) к множеству (7). получаем элемент oprnd с учетом частоты появления операндов данной семантики в программе.

Процедура внесения ДЕС в программу рассматривается в рамках следующих допущений:

• -    внесение ДЕС осуществляется для каждого оператора программы только одиножды с целью исключения компенсации дефектов;

• -    внесение ДЕС производится для любого одного элемента оператора (операции или операнда) с одинаковой вероятностью;

• -    внесение ДЕС выполняется безотносительно к порядку выполнения операций с операндами.

Порядок выполнения процедур методики оценки количества необнаруженных ДЕС программы с требуемой степенью доверия при верификации ПО представлен на рисунке.

Входными данными для методики являются: ИК программа ( sw ); количество «собственных» ДЕС, обнаруженных при верификации ( N О _БН), доверительная вероятность требуемая (β_ТРЕБ), доверительный интервал требуемый ( I ^ЕРЕБ ), размер начальной выборки ( K ).

Процедура 1 – получение статистики.

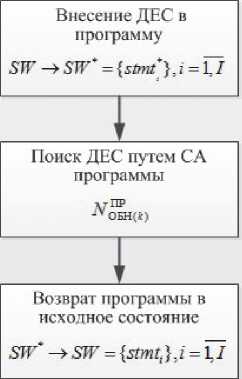
Данная процедура разбивается на три шага: внесение ДЕС в программу, поиск ДЕС и возврат программы в исходное состояние.

Первый шаг начинается с внесения ДЕС в оператор программы stmti . Для чего выполняется поиск точки преднамеренного внесения

Том 2

sir, к

VIT уПР

^*ОБН(Т) "'^'ОБЩТС)

^Статистическая обработка результатов

Р

Получение статистики

^

Да, необходимо

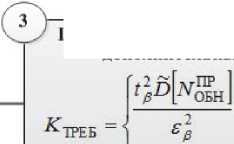
Проверка необходимости проведения дополнительных итераций

, если £„ > £я

К ре nil F < f™ /V . "-С ЛИ о g о р

Нет, достаточно

■ТРЕБ

2_

Расчет количества необнаруженных ДЕС нротраммы

^v НЕ ОБН

ОБН

С _т

ОБН

Рис. 1

дефекта pnt_i , которая выбирается из множества возможных точек для данного оператора

PNT i = OPR ^ U opr i ^П U opr i ^С U OPRND, : pnti = rnd ⁽ PNT i).

Далее в зависимости от принадлежности pnt_t к одному из множеств

( OPR а , OPR _п, OPR _с, OPRND bx )

выбирается один из элементов соответствующего множества, за исключением pnt_i , и используется в качестве дефекта: def = rnd ( SET \ pnt i ).

В результате вместо исходного оператора программы stmti имеется stmt_t , у которого в одном из элементов описывающего его кортежа в точке pnt_i существует дефект def_i : stmt_i → stmt_i ^* . Выполнив внесение ДЕС для каждого оператора, получаем программу, в каждом операторе которой имеется дефект операции или операнда, распределённый равномерно:

SW ^ SW* = {stmt*}, i = 1,I.

На втором шаге производится обнаружение ДЕС с помощью методики СА для их поиска N ОБН k ). „

Третий шаг заключается в возвращении программы в исходное состояние _

SW * ^ SW = { stmt i }, i = 1, I .

Шаги процедуры 1 выполняются K раз согласно заданному размеру начальной выборки.

Процедура 2 – статистическая обработка результатов.

Выполняется расчет следующих статистических характеристик [8]:

M [NПРН ] = K"' Е Nобн(k) — оценка МОЖ k=1 количества обнаруженных дефектов в серии из K итераций внесения дефектов;

D) [ N 1_Н 1 = ( K - 1)^-1 K (N _o1    - Mt [ N И_БН ]) 2

I ОБН I V /   ' ОбН(k)          ОбН k=1

• -    оценка дисперсии количества обнаруженных де-

• фектов в серии из K итераций внесения дефектов;

^{а [} N ПН ] = K "' V D * ^[ N о™1 ^- среднее ^квадратическое отклонение оценки МОЖ количества обнаруженных дефектов в серии из K итераций внесения дефектов.

При допущении о нормальном распределении N 0>bh ( K - 20—30) по таблице из [8] определяется значение величины t _β, соответствующее требуемому значению доверительной вероятности β ТРЕБ .

Рассчитывается величина половины длины доверительного интервала для МОЖ количества обнаруженных дефектов в серии из K итераций внесения дефектов: ер = tро[NПБН]-

Процедура 3 – проверка необходимости проведения дополнительных итераций внесения дефектов.

Осуществляется сравнение значения ε_β с требуемым значением Е Т = I р ¹ /2.

Если Е р <  Ер , то рассчитанная оценка МОЖ количества обнаруженных «преднамеренных» дефектов считается совместной с данными,

полученными в серии из K итераций внесения де-

фектов, согласно размеру начальной выборки.

Если

^Е Р

ТРЕБ

>^Е Р

то получен доверитель-

ный интервал для оценки МОЖ количества обнаруженных «преднамеренных» дефектов больше требуемого, что говорит о недостаточной репрезентативности рассматриваемой статистики дефектов и необходимости проведения дополнительных итераций внесения дефектов.

Для получения выборки требуемого раз-

мера K _ТРЕБ используется система соотношений:

^K ТРЕБ

t ² ( ^Е 2 ) 1 D [ N ПН ] K , если Е р < Е ТРЕБ

если Е р > Е р

Количество дополнительных итераций внесения дефектов рассчитывается по следующему соотношению: K ДОП = K _ТРЕБ - K .

Если K _ДОП > 0, то необходимо вернуться к процедуре 1. Выполняется K д_ОП итераций внесения дефектов и обрабатывается полученная статистика величиной K _ТРЕБ.

Процедура 4 - расчет количества необнаруженных ДЕС программы с требуемой степенью доверия.

Используя полученную оценку МОЖ количества обнаруженных «преднамеренных» дефектов для выборки требуемого размера K _ТРЕБ , при условии, что N ПБщ = | $^ |, рассчитывается количество необнаруженных ДЕС программы по соотношению (4).

Представленный методический подход к оценке количества необнаруженных ДЕС программы с требуемой степенью доверия при верификации ПО БЦВС КА разработан с целью приведения в соответствие нормативным документам создаваемого метода верификации ПО и позволяет выполнять доказательство отсутствия дефектов рассматриваемого типа после выполнения их поиска путем СА с требуемой степенью доверия в рамках испытаний ИК программ.