Методический подход к определению точности радиоэлектронной разведки с учетом обеспечения требуемой эффективности радиоэлектронного подавления и радиоэлектронной защиты

В современных условиях радиоэлектронно-информационного конфликта [1, 2] основной проблемой является обеспечение требуемой точности радиоэлектронной разведки (РЭР) для достижения высокой эффективности радиоэлектронного подавления (РЭП). Однако стремление к повышению точности разведки неизменно приводит к возрастанию времени проводимых для ее осуществления мероприятий, что вызывает потерю оперативности действий по РЭП. Возможный способ компенсации недостаточной точности РЭР – расширение спектра помеховых сигналов, что неизменно влечет за собой обострение проблемы радиоэлектронной защиты (РЭЗ) своих радиоэлектронных средств (РЭС). Для обоснования рациональных способов повышения эффективности РЭПр с учетом обеспечения заданных требований по РЭЗ своих средств требуется разработка соответствующего методического обеспечения.

Цель работы – разработка методики оценки предельных ошибок определения несущей частоты РЭС противника и возможности их компенсации для обеспечения требуемой эффективности РЭП с учетом требований по РЭЗ наших РЭС.

Постановка задачи

Считаем, что РЭС противника работает на частоте f 0 . Нормированная АЧХ приемника РЭС имеет колоколообразную форму (рис. 1) и равна

4( f - f 0 ) ² _-

H 0 ( f ) = e ^{Δ F 02} ,                                                          (1)

где f – несущая частота сигнала РЭС противника; Δ F – ширина полосы пропускания приемника РЭС противника по уровню 1/ e .

Средство РЭБ осуществляет разведку сигнала, определение его параметров и формирование согласованной по спектру помехи. При этом определение несущей частоты сигнала происходит с ошибкой Δ f . Нормированная спектральная плотность мощности сигнала помехи в таком случае имеет вид

_- 8( f - f ₀ -Δ f ) ²

G п ( f ) = e      ^{Δ F п2}     ,                                                          (2)

где Δ F П – ширина спектра помехи по уровню 1/ e , Δ F П ≥ Δ F 0 .

Задачей РЭП является обеспечение максимальной мощности помехи P _П на выгоде согласованного приемника РЭС противника. Очевидно, что, имея априорную информацию о статистических характеристиках ошибок определения несущей частоты сигнала РЭС противника, можно компенсировать снижение мощности помехового сигнала на выходе согласованного фильтра за счет расширения спектра помехи Δ F . Однако при этом возникает задача электромагнитной совместимости (ЭМС) со своими средствами радиосвязи, которые тоже будут подвержены воздействию помехи.

Будем рассматривать случай работы нашей РЭС на несущей частоте, отстоящей от несущей частоты работы РЭС противника на некоторую частоту разноса f ≥ 2Δ F . Нормированную АЧХ приемника нашего РЭС представим в виде

2 - 4(f ff,)

H i ( f ) = e     ^A F ¹      ,                                                       (3)

где Δ F 1 – ширина полосы пропускания приемника нашего РЭС по уровню 1/ e .

Тогда задачу оценки предельных ошибок определения несущей частоты РЭС противника и возможности их компенсации с учетом условий ЭМС можем сформулировать следующим образом. Для заданных АЧХ приемников РЭС противника H ₀( f ) и нашего РЭС H ₁( f ), разнесенных на частоту разноса f р , а также спектральной плотности мощности помехи G П ( f ) рассчитать пре-

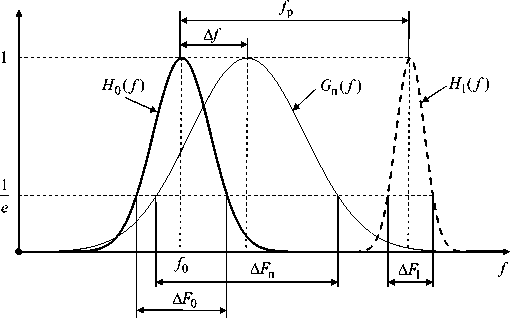
Рис. 1. АЧХ приемников РЭС и АЧХ спектра помехи дельные значения СКО ошибок определения несущей частоты РЭС противника σf и возможности их компенсации за счет расширения спектра помехи ΔFП, при которых обеспечивается требуемое ограничение по снижению мощности помехи на выходе приемника РЭС противника и выполняется условие ЭМС со своим РЭС – ограничение по мощности мешающего помехового сигнала на выходе приемника нашего РЭС.

Определение предельных абсолютных ошибок разведки несущей частоты сигнала РЭС

В общем случае мощность помехового сигнала на выходе линейной цепи с учетом формирования согласованной по спектру помехи равна [3]

_{Ю                    Ю} - ⁸⁽ f - f 0 ^- A f ⁾² - ⁸

P n = J G n ( f ) H 0² ( f ) df = J e      ^A F п         ^{A F 0} df -                 (4)

—00                       —00

∞∞

После интегрирования выражения (4) и выполнения преобразований получим зависимость нормированной мощности помехи на выходе приемника РЭС противника от ошибки определения несущей частоты:

_ 2^2   -   ^{8 A f 2}

P n ( A f ) =

^ ^ F O ^{A F} n e ( A F o ² +A F _n ² )

4( A F o² +A F n² )

Введем в рассмотрение коэффициент перекрытия помехой сигнала РЭС противника, равный отношению ширины спектра помехи к ширине полосы пропускания РЭС противника:

K

п

A ^ n

A F o

Тогда выражение (5) примет вид

P n ( A f ) =

«A F 2  -AF O ⁸^

4(1 + K - 2 ) e

При нулевой ошибке определения несущей частоты приемника РЭС противника нормированная мощность помехи максимальна и равна

-

sAf2

P n^{( A f} ) _ _e A F o² (1 + K п² )

P o

P _п

-

Alexander A. Dontsov, Yuri L. Koziratsky… A Methodical Approach to Determine the Accu-racy of Electronic… _

Из выражения (9) видно, что снижение мощности помехи при увеличении ошибок определения несущей частоты приемника РЭС противника может быть компенсировано увеличением коэффициента перекрытия помехой сигнала РЭС противника, т.е. увеличением ширины спектра помехи.

Аналогичным образом определим мощность мешающего помехового сигнала на выходе приемника нашего РЭС:

р

м

⁷               1

^J G п ( f ) H 1⁽ f ) ^df

-7

4( f — f o —A f ) 2 4( f — f о — f р ) 2

7AV

-L e         п             ^{1 df}

Зависимость нормированной мощности помехи на выходе приемника нашей РЭС от ошибки определения несущей частоты определяется выражением

P m ( A f ) =

2 2     - ^{8( f} р ^{-A f} ) 2

^{nA F} 1 "F e ^{( A F} i2 ^{+A F} -) 4( A F 1² +A F _n ² )

Введя в рассмотрение коэффициент перекрытия мешающей помехой сигнала нашей РЭС –

A^n

K м = ттп, получим:

A F 1

P m ( A f ) =

_ ⁸⁽ f р ^-A f ) ²

^^ F Y    e AF?(1+K M )

4(1 + K M2 )

Тогда доля нормированной мощности мешающей помехи, попадающей в полосу пропускания приемника нашего РЭС, равна

P m ( A f )

м

_ 8( f р -A f ) ²

= e A F 2 (1 + K M )

.

На рис. 2 представлены графики зависимостей относительной мощности помехи в при-

PP емнике РЭС противника п (сплошные линии) и в приемнике нашего РЭС м (пунктирные Pп0                                          Pм0

линии) от отношения ошибки определения несущей частоты сигнала РЭС противника к часто- те разноса , рассчитанные для различных значений коэффициента перекрытия K = K = K fр при ΔF0 = 2ΔF1; fр = 2ΔF0.

Зависимости на рис. 2 позволяют оценить предельные значения абсолютных ошибок определения несущей частоты сигнала РЭС противника для обеспечения заданных требований ЭМС. Так, например, для того чтобы мощность мешающего помехового сигнала в приемнике – 215 – р р пм

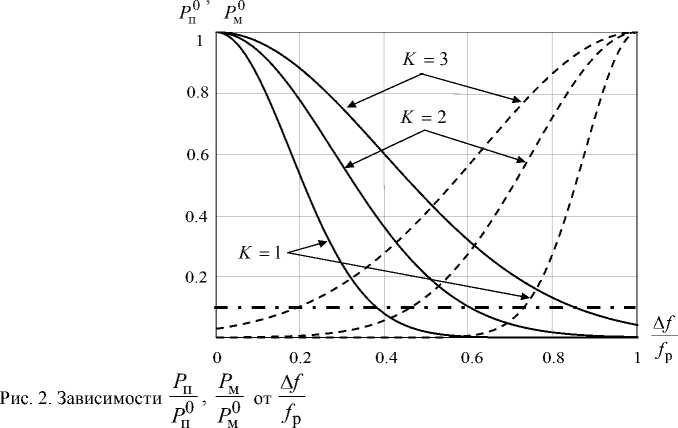
нашего РЭС не превышала 10 % (штрих-пунктирная линия на рис. 2), необходимо обеспечить определение несущей частоты с ошибкой не более 45 % от разноса частот работающих РЭС и станции помех для значения коэффициента перекрытия, равного 2. При увеличении коэффициента перекрытия до 3 ошибка определения несущей частоты не должна превышать 20 % от разноса частот.

Определение законов распределения относительных уровней мощности помех и мешающих сигналов

Считаем, что ошибки определения несущей частоты сигнала РЭС противника распределены по нормальному закону c нулевым математическим ожиданием:

Δ f ²

1        2 σ ²

ϕ ( Δ f ) = e ,                                                   (14)

2πσf где σf – СКО определения несущей частоты сигнала РЭС противника.

Применяя правила преобразования законов распределения случайных величин [4], найдем

P п ( Δ f )

₀ = P п : п

плотность распределения вероятности относительного уровня мощности помехи

Δ F 0 ² ln( P п ′ ) 1 + K п ²

g ( P п ′ ) =

Δ F 0 1 + K п²   _e     16 σ ² _f

4 σ _f - π ln( P _п ′ )

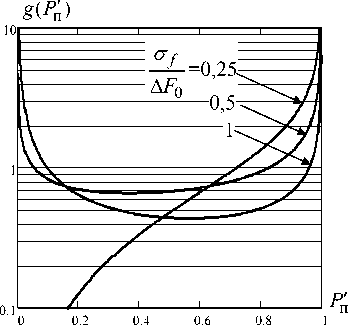
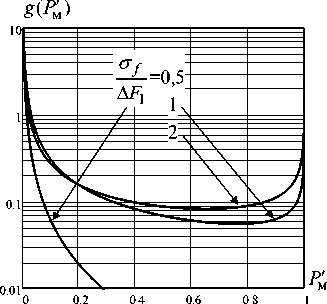
На рис. 3 представлены графики плотности распределения вероятности случайной величины P _п ′ , рассчитанные для различных значений отношения СКО ошибок определения несу-

σf щей частоты сигнала РЭС противника к ширине полосы пропускания его приемника:    . На

Δ F ₀

a) Kп=1     б) Kп=2

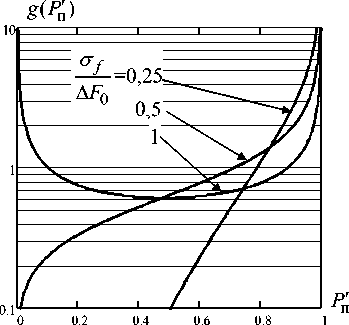
Рис. 3. Плотности распределения вероятности относительного уровня мощности помехи Pп′ рис. 3а представлены результаты расчетов для значения коэффициента перекрытия помехой сигнала РЭС противника КП = 1, на рис. 3б – для КП = 2.

На графиках рис. 3 видно, что при малых по отношению к полосе пропускания РЭС противника ошибках определения несущей частоты сигнала и при увеличении коэффициента перекрытия К _П вероятность высокого значения относительного уровня мощности помехи возрастает. При возрастании СКО ошибок определения несущей частоты сигнала РЭС противника наиболее вероятно снижение относительного уровня мощности помехи на выходе приемника.

Аналогично найдем плотность распределения вероятности относительного уровня мощ-

P м ( Δ f )

= P _м :

м

ности мешающей нашему РЭС помехи

₂    [ f р -Δ F 1 v    пп

g ( P м ′ ) =

Δ F 1 1 + K м² _e          2 σ ² _f

8 σ _f - π ln( P _м ′ )

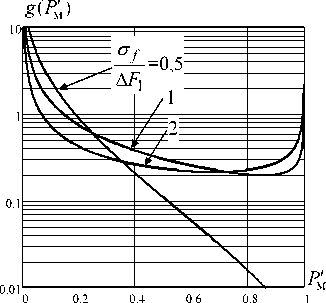
На рис. 4 представлены графики плотности распределения вероятности случайной величины P ′ , рассчитанные для различных значений отношения СКО ошибок определения несущей частоты сигнала РЭС противника к ширине полосы пропускания приемника нашего РЭС:

^{σ f} .

Δ F 1

На рис. 4а представлены результаты расчетов для значения коэффициента перекрытия мешающей помехой сигнала нашей РЭС К М = 1, на рис. 4 б – для К М = 3.

Видно, что при увеличении ошибок определения несущей частоты сигнала РЭС противника и увеличении значения коэффициента перекрытия мешающей помехой сигнала нашей РЭС, т.е. при увеличении ширины спектра помехи, возрастает вероятность повышения уровня мешающей помехи в приемнике нашей РЭС. Именно поэтому возникают ограничения на уве- – 217 –

a) Kм=1    б) Kм=3

Рис. 4. Плотности распределения вероятности относительного уровня мощности мешающей помехи Pп′ личение ширины спектра помехи при заданных параметрах частотного разноса РЭС и значениях СКО ошибок определения несущей частоты РЭС противника.

Оценка влияния ошибок определения несущей частоты РЭС на вероятностные показатели эффективности РЭП и РЭЗ

Оценим влияние ошибок определения несущей частоты РЭС противника на вероятность высокого относительного уровня мощности помехи на выходе приемника РЭС противника (не менее 0,8 от максимально возможного), а также на вероятность превышения относительного уровня мешающей помехи в приемнике нашего РЭС (более 0,1 от максимально возможного). На рис. 5 изображены зависимости вероятности P ( P _п ′ ≥ 0,8) (жирные линии) и P ( P _м ′ ≥ 0,1) (тонкие линии) от отношения СКО определения несущей частоты сигнала РЭС противника к ширине

σf полосы его пропускания , рассчитанные при различных значениях коэффициента пере-ΔF0

крытия K = K П = K М для случая Δ F 0 = Δ F 1 ; f р = 2Δ F 0 .

Анализ графиков показывает, что для обеспечения высокой (более 0,8) вероятности снижения мощности помехи не более чем на 20 % необходимо, чтобы значение СКО ошибок определения несущей частоты сигнала РЭС противника не превышало 15-20 % от ширины полосы пропускания приемника подавляемой РЭС. Если значение СКО ошибок определения несущей частоты сигнала РЭС противника достигает 30 % от ширины полосы пропускания приемника подавляемой РЭС, необходимо в 2 раза увеличивать ширину спектра помехи. Максимально возможное значение коэффициента перекрытия не должно превышать 2,5. В этом случае максимальное значение СКО ошибок определения несущей частоты сигнала РЭС противника может достигать 40 % от ширины полосы пропускания приемника подавляемой РЭС и вероятность того, что мощность мешающей помехи будет более 10 % от максимально возможного значения, не превысит значения 0,1.

P ( P п ′≥ 0,8), P ( P м ′ ≥ 0,1)

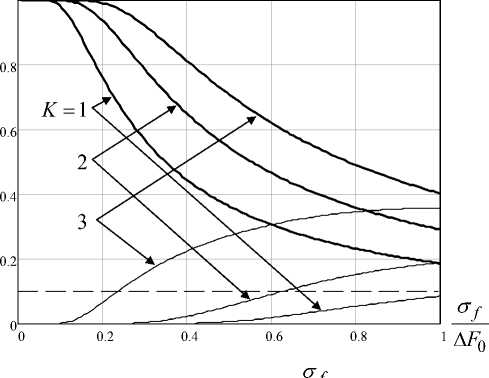
Рис. 5. Зависимости вероятностей P ( P _п ′ ≥ 0,8), P ( P _м ′ ≥ 0,1) от    ^f

Δ F ₀

Оценка предельных значений СКО ошибок определения несущей частоты РЭС

Оценим более точно предельные значения СКО ошибок определения несущей частоты сигнала РЭС противника и коэффициента перекрытия помехи. На рис. 6 представлены зависимости вероятности P ( P _п ′ ≥ 0,8) (жирные линии) и P ( P _м ′ ≥ 0,1) (тонкие линии) от значения коэффициента перекрытия K = K _П = K _М, рассчитанные для различных значений отношения СКО определения несущей частоты сигнала РЭС противника к ширине полосы его пропускания

σ f при ΔF0 = ΔF1; fр = 2ΔF0. ΔF0

P ( P п ′≥ 0,8), P ( P м ′≥ 0,1)

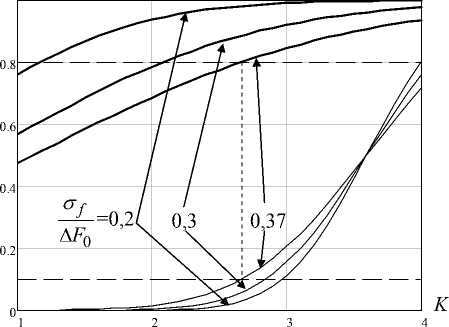
Рис. 6. Зависимости вероятностей P ( P _п ′ ≥ 0,8), P ( P _м ′ ≥ 0,1) от K

Расчеты показывают, что при равенстве полос пропускания приемников РЭС противника и нашего РЭС максимальное значение коэффициента перекрытия составляет 2,7. Это позволяет компенсировать ошибки определения несущей частоты сигнала РЭС противника, СКО которых составляет не более 37 % от ширины полосы пропускания подавляемого РЭС, и обеспечить заданные условия РЭП и ЭМС. Также в ходе исследований установлено, что при уменьшении полосы пропускания приемника нашего РЭС в 2 раза указанные предельные значения СКО ошибок определения несущей частоты сигнала РЭС противника и коэффициента перекрытия помехи увеличиваются незначительно.

Выводы

Таким образом, с использованием положений теории радиотехники и спектрального метода анализа прохождения сигналов через линейные цепи разработана методика оценки предельных ошибок определения несущей частоты РЭС противника и возможности их компенсации при условии обеспечения электромагнитной совместимости с соседним РЭС. На основе правил преобразования случайных величин получены аналитические выражения для расчета плотностей распределения вероятностей относительных уровней помехового сигнала на выходе приемника РЭС противника и мешающего помехового сигнала на выходе приемника нашего РЭС. При этом рассмотрен предельный случай минимального частотного разноса РЭС. Показано, что снижение мощности помехи при увеличении ошибок определения несущей частоты приемника РЭС противника может быть компенсировано увеличением коэффициента перекрытия помехой сигнала РЭС противника, т.е. увеличением ширины спектра помехи. Установлено, что при равенстве полос пропускания приемников РЭС противника и нашего РЭС максимальное значение коэффициента перекрытия равно 2,7. Это позволяет компенсировать ошибки определения несущей частоты сигнала РЭС противника, СКО которых составляет не более 35…40 % от ширины полосы пропускания подавляемого РЭС и обеспечить заданные условия радиоэлектронного подавления (снижение мощности помехи не более чем на 20 %) и радиоэлектронной защиты (уровень мешающей помехи не более 10 %).