Методический подход к улучшению работы генетического алгоритма в однородной минимаксной задаче
Автор: Кобак Валерий Григорьевич, Титов Дмитрий Вячеславович, Кобак Валерий Валерьевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 4 (47) т.10, 2010 года.
Бесплатный доступ
Дается оценка модификациям генетического алгоритма, решения которых очень близки к оптимальным за полиномиальное время. Эти алгоритмы приводят, в конечном счете, к решению двухприборной минимаксной задачи различными вычислительными путями.
Теория расписаний, задача планирования, трудоемкость решения, генетический алгоритм, списочные алгоритмы, вычислительный эксперимент, множество заданий, ядра процессора
Короткий адрес: https://sciup.org/14249383
IDR: 14249383 | УДК: 681.3+681.5
Текст научной статьи Методический подход к улучшению работы генетического алгоритма в однородной минимаксной задаче
Введение. Во многих отраслях промышленности часто применяются многопроцессорные (многоядерные) вычислительные системы для решения различного рода задач. При этом используют различные методы построения расписаний для эффективного решения таких задач, которые необходимо распределить по параллельно работающим процессорам (ядрам).
Построение оптимального расписания распределения заданий по процессорам относится к задачам NP -полным, т.е. трудоемкость решения распределительной задачи определяется по экспоненте как O ( n m ) , где O - временная асимптотическая сложность алгоритма, а n и m - целые числа больше единицы, обозначающие количество устройств и заданий соответственно, которые задают размерность распределительной задачи nm . Исследование теории расписаний помогает изучить фундаментальные свойства практических задач и направлено на построение более эффективных алгоритмов решения.
В настоящее время крупные производители процессоров Intel и AMD выпускают четырехъядерные процессоры. Однако AMD анонсировало выпуск шестиядерных процессоров, поэтому задача планирования распределения заданий по шести ядрам сейчас является крайне актуальной. Постановка задачи. Задача теории расписаний для однородных систем обработки информации может быть сформулирована следующим образом. Имеется однородная вычислительная система, состоящая из n идентичных параллельных процессоров (ядер) P = {p1,^,pn}, на которые поступает m независимых заданий Q = {q 1,...,qm}, образующих параллельную программу, причем известно время выполнения j-го задания (tj ) на любом из процессоров вычислительной систе- мы, где j = 1, m. В каждый момент времени отдельный процессор обслуживает не более одного задания, которое не передается на другой. Задача составления расписания сводится к разбиению исходного множества заданий на n непересекающихся подмножеств, т.е.
n
Q i : V i , j е [1, n ] > Q i П Q j = 0 и ^ Q i = Q . Критерием разбиения, обеспечивающего оптималь- i = 1
ность расписания по быстродействию, служит минимаксный критерий. Он определяет такое распределение заданий по процессорам, при котором время завершения T параллельной программы минимально, т.е. T = maxT!>min 1< i < n
где Ti = ^ tj - загрузка i-ого процессора (время оконча-tj eQi ния выполнения множества заданий Qi с Q, назначенных на процессор pi, где i = 1,n) [1].
Методы решения распределительной задачи. Методы решения однородных распределительных задач можно разбить на два класса. Первый класс – это точные методы, к которым относятся метод полного перебора, алгоритм Романовского, алгоритм Алексеева. Второй – приближенные методы (списочные и эвристические). Списочные методы – метод критического пути, ал- горитм Пашкеева и др. Эвристические методы – генетические алгоритмы, метод отжига, метод роящихся частиц и др.
Для получения оптимального решения однородной распределительной задачи используются точные методы решения. С увеличением размерности, в силу ее NP -полноты, а также при сужении диапазона ресурсных оценок распределяемых заданий оптимальное решение за доступное время может стать недостижимым. В этой ситуации приходится ориентироваться на быстрые, но приближенные методы, позволяющие получить решение близкое к оптимальному, такие, как генетические алгоритмы.
Списочные методы. Списочные методы отличаются простотой в построении и реализации, характеризуются высокой эффективностью и оптимальным временем выполнения. Физический смысл списочных расписаний заключается в распределении работы на устройства, на данный момент наименее загруженные, а общее время выполнения будет близким к минимальному. Реализация списочных расписаний основана на применении линейных списков работ, упорядоченных по убыванию приоритета в соответствии с принятым алгоритмом выбора работ.
Одним из самых распространенных списочных алгоритмов является метод критического пути – Critical Path Method (CPM). Принцип действия CPM заключается в том, что очередное задание из списка заданий, упорядоченных по убыванию, назначается на процессор с самой минимальной суммарной загрузкой. Для данного метода имеется теоретически вычисленная максимальная оценка погрешности, которая не зависит от количества распределяемых работ или их размера. Уровень точности задается соотношением FCPM /F0 ≤4/3-1/3n, где FCPM - решение, полученное с помощью CPM, F0 - точное решение [1]. Следовательно, lim FCPM /F0 ≤ 4/3, n→∞ т.е. при росте размерности задачи погрешность не будет превышать 0,33. Данный факт позволяет использовать CPM в качестве базового алгоритма при сравнительном анализе приближенных и вероятностных алгоритмов на задачах большой размерности.
Генетические алгоритмы. К одним из самых популярных эвристических методов относятся генетические алгоритмы (ГА), которые являются одной из парадигм эволюционных вычислений, построены на принципах, сходных с принципами естественного отбора и генетики. Общий принцип работы ГА состоит в следующем: на первом шаге формируется начальное поколение, состоящее из заданного числа особей; на втором происходит отбор особей и применение операторов кроссовера и мутации ГА с заданной вероятностью, формирование нового поколения; на шаге три проверяются условия останова, которая обычно заключается в неизменности лучшего решения в течение заданного числа поколений, если проверка прошла успешно, то лучшая особь выбирается как найденное решение, иначе происходит переход на второй шаг. Такая схема является наиболее общим алгоритмом для решения разнотипных задач. В данном случае, при решении задачи теории расписания минимаксный критерий будет являться оптимизационной функцией, а условием останова будет неизменность лучшего решения в течение заданного числа поколений. При отборе родительских пар для оператора кроссовера берется текущая и случайно выбранная особь из исходного вектора особей. Для формирования нового поколения используется турнирный отбор, когда из заданного числа особей (в данном случае две ) выбирается лучшая, которая перейдет в новое поколение. Лучшей особью считается та, для которой значение оптимизационной функции минимально.
Модификации генетического алгоритма. Была предложена модификация ГА [2], когда при формировании нового поколения использовался бинарный турнирный отбор, в котором участвовала очередная особь, т.е. родительская, и результирующая, полученная в ходе выполнения операторов кроссовера и мутации. Данная модификация давала самый лучший результат из рассмотренных [2]. Предложенный способ формирования нового поколения называется турнир с родителем.
Декомпозиционный подход к решению распределительных задач с четным количеством процессоров заключается в следующем [3]: вначале распределяется m заданий с помощью ГА на k процессоров, где k = n /2, получается k непересекающихся подмножества заданий, т.е. Q 1 U Q 2 U^U Q k = Q . Далее распределяется, применяя ГА, каждое подмножество заданий
Q 1 ,Q 2 , ..., Q k на два процессора, в результате получается 2 k = n непересекающихся подмножества заданий, т.е. Q 11 U Q 12 = Q 1 , ..., Q k 1 U Q k 2 = Q k , образующих расписание для n - процессорной вычислительной системы, т.е. Q 11 U Q 12 U.U Q k 1 U Q k2 = Q . Данная модификация показала наилучшие результаты из рассмотренных модификаций ГА для четного количества процессоров [3]. Причем, если в результате выполнения данного алгоритма получается, что к = n /2 является четным числом, то для распределения m заданий на к процессоров вызывается рекурсивно данный алгоритм. Этот подход получил название метод бинарной декомпозиции с использованием ГА (МБД ГА).
Также авторами анонсирован новый декомпозиционный подход к решению однородных распределительных задач, заключающийся в поэтапном снижении размерности распределительной задачи путем понижения количества процессоров от n до двух с сохранением на каждом этапе лучшего распределения заданий на одном из процессоров. Для этого вначале вычисляется m теоретически возможное минимальное решение Tmin = ^ tj /n . Затем, распределяются задания j=1
с помощью ГА по n устройствам. Вычисляется, насколько загрузка каждого устройства отличается от Tmn , т.е. A T i = | T - Tmn I , где T i - загрузка i - го устройства. Множество заданий Q n , назначенных на устройство с самой минимальной разностью A T , запоминается, а остальные задания распределяются с помощью ГА по n - 1 устройствам. Затем также вычисляется A T и множество заданий Q n - 1 , назначенных на устройство с самой минимальной разностью A T i , запоминаются, а остальные задания распределяются с помощью ГА по n - 2 устройствам и так далее. Данная последовательность действий выполняется пока n > 2 , затем с помощью ГА распределяются оставшиеся задания на два устройства, получается два множества заданий Q 1 и Q 2 . В итоге множества заданий, которые запоминались и два последних, образуют расписание для n -процессорной вычислительной системы, т.е. Q n U Q n - 1 U.U Q 2 U Q 1 = Q . Данный подход обозначим как метод декомпозиции с использованием ГА (МД ГА).
Анализ эффективности генетических относительно списочных алгоритмов. Для сравнения эффективности генетических алгоритмов по отношению к списочным был проведен вычислительный эксперимент. Количество элементов системы параллельной обработки информации – от 2 до 6 процессоров. Количество работ, которые распределялись между процессорами, – 19 и 119. Для проведения эксперимента были случайным образом сгенерированы 100 векторов загрузки, содержащие работы в диапазоне [25, 30], каждый из векторов решался CPM и ГА, с использованием турнира с родителем. Для ГА были выбраны следующие фиксированные параметры: число особей – 50, условие останова – появление в процессе решения более 500 поколений с лучшей одинаковой особью, вероятность кроссовера – 90 %, а вероятность мутации – 10 %. Полученные 100
результаты усреднялись по количеству экспериментов, т.е. T ср = ^ T i /100. Для оценки эффек- i = 1
тивности рассматриваемых алгоритмов приведен график зависимости A T = T Ср PM - T СрА (см. рисунок), где T Ср PM - усредненный результат для CPM, T сГА - усредненный результат для ГА, с использованием турнира с родителем
Таким образом, проанализировав результаты, приведенные на диаграмме, можно отметить, что наиболее перспективной для финальной работы генетических алгоритмов является двухприборная система обработки информации. Именно при таком количестве приборов происходит наибольшее приближение к оптимальному распределению.
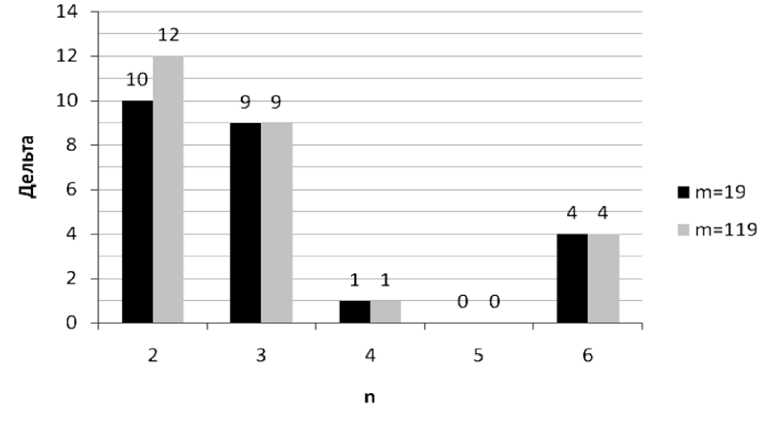
Сравнение ∆ T для CPM и ГА
Экспериментальное сравнение генетических алгоритмов. Так как задача планирования распределения заданий по шести ядрам сейчас является крайне актуальной, то для анализа эффективности генетических алгоритмов был проведен вычислительный эксперимент для процессорных систем обработки информации состоящих из шести элементов, количество работ, которые распределялись между процессорами, составляло 19 и 119. Для проведения эксперимента были случайным образом сгенерированы 100 векторов загрузки, содержащие работы в диапазоне [25, 30], каждый из векторов решался ГА, МБД ГА и МД ГА. Для всех ГА были выбраны следующие фиксированные параметры: число особей составляло 50, условием останова являлось появление в процессе решения более 500 поколений с лучшей одинаковой особью, вероятность кроссовера составляла 90 %, а вероятность мутации 10 %. Полученные результаты усреднялись по количеству экспериментов (см. табл.).
Экспериментальное сравнение генетических алгоритмов
|
n |
m |
Усредненное решение |
Усредненное время решения задач, мс |
||||
|
ГА |
МБД ГА |
МД ГА |
ГА |
МБД ГА |
МД ГА |
||
|
6 |
19 |
102,85 |
101,31 |
101,23 |
26 |
57 |
91 |
|
119 |
550,61 |
545,57 |
547,65 |
161 |
257 |
495 |
|
Можно отметить, что при малом количестве заданий алгоритм МД ГА является наиболее эффективным. Но с увеличением количества заданий наиболее эффективным становится алгоритм МБД ГА.
Выводы. При большом количестве заданий и четном количестве приборов наиболее перспективным для решения однородной минимаксной задачи является МБД ГА. Однако данный алгоритм не приспособлен для решения задач с нечетным количеством приборов. В этом случае наиболее пригоден алгоритм МД ГА. Списочным алгоритмом можно пользоваться для получения быстрой вспомогательной оценки.
Список литературы Методический подход к улучшению работы генетического алгоритма в однородной минимаксной задаче
- Коффман Э.Г. Теория расписания и вычислительные машины/Э.Г. Коффман. -М.: Наука, 1987. -334 с.
- Нейдорф Р.А. Сравнительный анализ эффективности вариантов турнирного отбора генетического алгоритма решения однородных распределительных задач/Р.А. Нейдорф, В.Г. Кобак, Д.В. Титов//Вестник ДГТУ. -2009. -Т. 9. -№ 3. -С. 410-418.
- Титов Д.В. Модификация генетического алгоритма распределения для четного количества однородных приборов/Д.В. Титов//Изв. вузов. Северо-Кавк. регион. Технические науки. -2010. -№ 1. -С. 3-6.
- Koffman E.G. Teoriya raspisaniya i vychislitel'nye mashiny/E.G. Koffman. -M.: Nauka, 1987. -334 s. -in Russian.
- Neidorf R.A. Sravnitel'nyi analiz effektivnosti variantov turnirnogo otbora geneticheskogo algoritma resheniya odnorodnyh raspredelitel'nyh zadach/R.A. Neidorf, V.G. Kobak, D.V. Titov//Vestnik DGTU. -2009. -T. 9. -№ 3. -S. 410-418. -in Russian.
- Titov D.V. Modifikaciya geneticheskogo algoritma raspredeleniya dlya chetnogo kolichestva odnorodnyh priborov/D.V. Titov//Izv. vuzov. Sev.-Kavk. region. Tehnicheskie nauki.-2010. -№ 1. -S. 3-6. -in Russian.


