Методика анализа достоверности вариантов оптимизации инвестиционных проектов

оценить целесообразность и эффективность предложенного варианта осуществления ИП. Так как модель ЧДД относительно таких факторов, как условно-постоянные затраты А i и объем продаж X i на i -м шаге проекта линейна, то результирующее изменение ЧДД будет равно сумме изменений ЧДД под влиянием этих факторов:

А ЧДД - вЧД AA, + вД АХ +

+ вД АХ1+,+ РТ АХ^    ,

1 X i + 1         i + 1      • X i + 2        i⁺2

где АЧДД - результирующее изменение ЧДД вследствие изменения факторов A i , X i , X i+1 , X i+2 .

В общем случае при наличии совокупности возмущающих факторов модель расчета результирующего изменения ЧДД имеет вид:

nm

А ЧДД - ^^ р ЧДД A F ki i - о k -1 ^z (3)

где в ЧЧД^Д — модель чувствительности ЧДД к фактору F k на i -м шаге проекта; m – количество анализируемых возмущающих факторов проекта.

Если результирующее изменение ЧДД проекта в результате воздействия совокупности анализируемых возмущающих факторов больше нуля, то данный вариант реализации ИП приведет к увеличению значения ЧДД и должен быть принят к осуществлению. В случае, если результирующее изменение ЧДД меньше нуля, то данный вариант реализации ИП приведет к уменьшению значения ЧДД и должен быть отвергнут. Предложенная модель (3) справедлива для факторов, линейно входящих в модель (1). Совершенно иная ситуация складывается в случае нелинейных взаимозависимостей. Так, например, выручка от реализации продукции вычисляется как произведение цены реализации и объема продаж продукции, а переменные затраты – как произведение норматива условно-переменных затрат на объем производства. В силу этого модель ЧДД относительно цены реализации и объема производства продукции (также, как и для норматива условно-переменных затрат на выпуск единицы продукции и объема производства), при их одновременном изменении на одном и том же шаге проекта, является нелинейной. В этом случае модель изменения ЧДД при возмущении двух факторов F1 и F2, входящих в модель расчета ЧДД как произведение на одном и том шаге проекта, будет иметь вид:

A хАА = A хАА"  + A xAA _F + ^A F 1 i ^A F

^F'              F ² '     (1 + a) '

= p4™ AFXi + вД AF2i+ —1—2^,      (4)

^P F ¹ '      1'               2'    (1 + a ) '

где ΔЧДД – изменение ЧДД вследствие изменения факторов F 1 и F 2 на i- м шаге; A ЧДД f - изменение ЧДД вследствие изменения фактора F 1 на i- м шаге; A ЧДД_F - изменение ЧДД вследст-

AF iAF2i вие изменения фактора F на i-м шаге; 1i 2i -2                    (1 + a)i остаточный член.

С учетом моделей (3) и (4), многофакторная модель анализа чувствительности ЧДД к действию совокупности возмущающих факторов примет вид:

A ЧДД = в Ч Д^ AF_U + в^ A F 2 ' + в ^Д A F₃ ' +

+ в ЧД a f ₄ ' +

A F 3' A F₄ ' ( 1 + a )

+ ...,

где F1 и F2 – возмущающие факторы, не входящие в модель расчета ЧДД как произведение на i-м шаге проекта; F3 и F4 – возмущающие факто- ры, входящие в модель расчета ЧДД как произведение на i-м шаге проекта.

Значение предложенной модели. Аналитическая модель (5) анализа чувствительности ЧДД к действию совокупности возмущающих факторов является основой методики для анализа достоверности вариантов оптимизации проектов, рекомендуемых к реализации. Модель позволяет решать задачи анализа вариантов реализации проектов, оценивать целесообразность и эффективность предложенного варианта реализации проекта путем оперативного определения значения ЧДД при изменении значений возмущающих факторов. Изложенный выше аппарат позволяет проводить анализ сценариев развития событий по принципу: «что будет, если проект осуществлять по первому варианту, а что будет, если по второму». Выходная характеристика разработанной модели (5) представляет собой рассчитанную разность ЧДД проекта до и после внесения изменений в первоначальный (базовый) вариант реализации проекта. Предложенная модель анализа чувствительности ЧДД к действию совокупности возмущающих факторов позволяет решать следующие задачи синтеза значений факторов для достижения требуемого значения ЧДД проекта:

• 1.    При заданном значении возмущающих факторов вычислять аналитически такое критическое значение одного из факторов, при котором ЧДД проекта равен нулю, т.е. проект находится на границе устойчивости. Таким образом, решается задача анализа устойчивости проекта к изменению одного из факторов.

• 2.    Позволяет получить аналитическую и графическую зависимость одного из факторов проекта от значения другого при неизменном значении ЧДД.

  

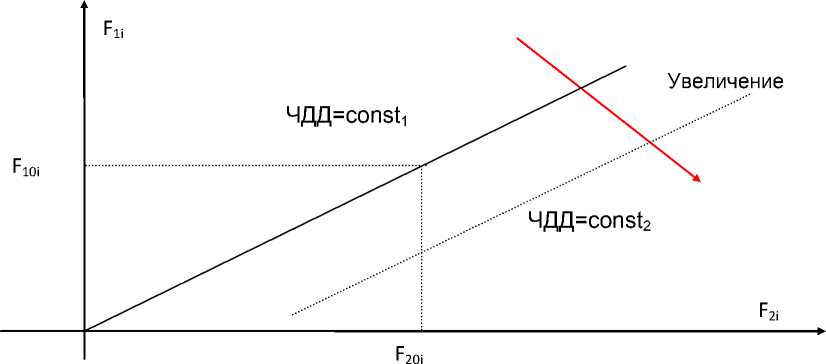
  Рис. 1. Графологическая модель зависимости фактора F 1i, влияющего на поток доходов, от фактора F 2i , влияющего на поток затрат, при неизменном значении ЧДД

  
  

Отметим, что возмущающие факторы разбиты на две группы: группу факторов, влияющих на поток доходов, и группу факторов, влияющих на поток затрат. В соответствии с этим рассмотрим характер зависимости между факторами для первого варианта, когда факторы относятся к разным группам. При увеличении значения фактора F2i на AF2i изменение ЧДД составит А ЧДД^ = РЧДAF2i. Для компенсации этого влияния изменим значение фактора F1i на AF1i так, чтобы изменение ЧДД составило А ЧДДaf , = nFV AF и значение ЧДД осталось на прежнем уровне. На основании модели изменение А ЧДДAF1i примет вид:

А ЧДД а^ = в ЧД A F ii =A ЧДД af₂₁ = в ЧДД A F 2 i 1 i            1 i                                        2 i            2 i

,

Откуда искомое значение F 1i равно:

Р ЧДД

F11i = F10 i + ЧДД AF2 i в^      ,              (7)

При условии сохранения постоянного значения ЧДД графологическая модель зависимости фактора, влияющего на поток доходов, от фактора, влияющего на поток затрат, при линейности модели ЧДД относительно анализируемых факторов, имеет вид прямо пропорциональной зависимости (см. рис. 1).

При увеличении значения ЧДД (под действием остальных факторов) графологическая модель будет сдвигаться вниз по оси ординат

(см. рис. ЧДД=const 2 ). Тангенс угла наклона (k) линии графологической модели зависимости фактора F 1i от фактора F 2i равен:

Р ЧД^Д

^F 1 i

P™

Данный результат в определенной степени соотносится с известной в микроэкономике задачей взаимозаменяемости ресурсов.

Рассмотрим характер зависимости между факторами для второго варианта, когда факторы относятся либо к одной группе факторов, влияющих только на поток доходов, либо к группе факторов, влияющих только на поток затрат. При условии сохранения постоянного значения ЧДД, графологическая модель зависимости фактора, влияющего на поток доходов, от фактора, также влияющего на поток доходов, при линейности модели ЧДД относительно анализируемых факторов, имеет вид обратной зависимости. При увеличении значения ЧДД (под действием остальных факторов) графологическая модель будет сдвигаться вниз по оси ординат ЧДД=const 2 .

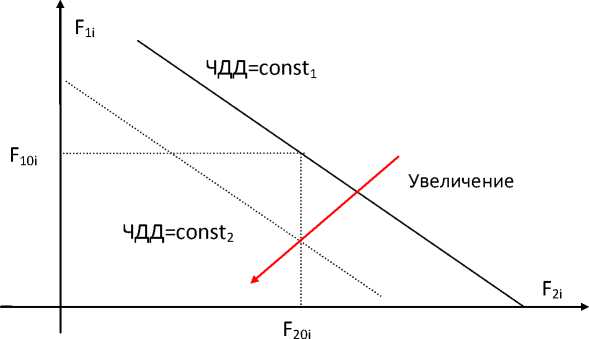
Рис. 2. Графологическая модель зависимости фактора F 1i от фактора F 2i при неизменном значении ЧДД

Данные модели чувствительности позволяют получить количественную меру влияния значения одного из факторов проекта на значение другого; получить вид функциональной зависимости значения одного фактора от значения другого. Это обеспечивает не только решение задач анализа, но и синтеза взаимозависимости факторов.

Продолжая изложение перспектив использования данных моделей, отметим возможности их применения для синтеза такого значения одного из факторов при заданном значении остальных факторов, которое обеспечит требуемое значение ЧДД. Например, значение фактора F 11i на i- м шаге проекта, при котором значение ЧДД проекта будет равно значению ЧДД 2 , вычисляет-

^F 11 i = ^F 10 i

—

ЧДД 2 — ЧДД + в ЧДД A F ₂ i + в ЧДД A F 3 i 2 i                      3 i

в Д

ся по модели:

+ в ЧД^Д A F _4z+^{A F} 3 i ^{A F} 4 i - + ... ^e F 4 i     ^{4 i}    ( 1 + a ) ⁱ

,

где F 11i – значение фактора F 1 на i- м шаге, при котором ЧДД равен ЧДД 2 ; F 10i – первоначальное значение фактора F 1 на i-м шаге проекта.

И, наконец, последний и наиболее существенный элемент, отражающий практическую направленность использования разработанных моделей, заключается в способности аналитически решать задачи оптимизации вариантов реализации ИП по разработанной модели при наличии информации о виде функциональной связи между анализируемыми факторами, путем синтеза такого значения изменения фактора, при котором ЧДД проекта достигает максимума.

Методика анализа и оптимизации. Предложенная модель анализа чувствительности ЧДД к действию совокупности возмущающих факторов легла в основу методики анализа и оптимизации вариантов реализации ИП. Методика является не только инструментом поддержки принятия решений на прединвестиционной фазе проекта, но и инструментом разработки маркетинговых стратегий развития действующих предприятий, планирования и разработки стратегических и тактических планов продаж, разработки и оптимизации стратегии поведения при смене стратегии конкурентов, изменении факторов внешней среды и т.д. Методика содержит следующие этапы:

• 1.    Разработка модели расчета ЧДД, по которой проводится расчет ЧДД для базового варианта проекта.

• 2.    Выбор анализируемых возмущающих факторов и вида функциональной связи между ними.

• 3.    Построение моделей чувствительности ЧДД к изменению анализируемых возмущающих факторов.

• 4.    Проверка наличия линейной зависимости ЧДД от анализируемого возмущающего фактора. В случае, если модель расчета ЧДД проекта не линейна относительно анализируемого возмущающего фактора, то разработанная на ее основе модель чувствительности ЧДД к соответствующему возмущающему фактору будет вносить ошибку в результат анализа.

• 5.    Построение модели реакции ЧДД на возмущения анализируемых факторов на основе модели

• 6.    Расчет по полученной модели необходимых значений анализируемых возмущающих факторов в соответствии с поставленной задачей и интерпретация результатов.

Здесь возможны следующие варианты:

• ■    постановка задачи многофакторного анализа чувствительности ЧДД к действию возмущающих факторов;

• ■    постановки задачи синтеза значения возмущающего фактора для достижения требуемого значения ЧДД.

Во втором случае можно решить задачу устойчивости ИП к изменению возмущающего фактора, задачу синтеза значения возмущающего фактора для достижения оптимального (максимального) значения ЧДД.

Выводы: предложенные модели анализа достоверности вариантов инвестиционных проектов могут служить инструментом решения задач принятия управленческих решений.