Методика анализа и формирования размерных цепей в технологиях агрегатно-сборочного производства летательных аппаратов

Модель системы ТП сборки в виде графа позволяет ввести индексные функции показателей производственных переходов в виде связей по дугам графа f_i(x_i,j), которые могут иметь достаточно сложный вид, если функции задаются аналитически или алгоритмически. Процессы преобразований сборочного пространства при выполнении сборочных операций представим как n-шаговый процесс реализации решений с операторами переходов A- = f ( s ^, u^ = x^ + u j = x , где результат перехода определяется функцией:

f (^--1,uj^ = f {x-1,x(u7)} .

зуют вектор замыкающего звена АДк, который определяет положение конца последнего составляющего звена цепи относительно начала первого звена. Положение вектора замыкающего звена в пространстве определится проекцией линии L на направление замыкающего звена в исходной системе координат X0, Y0, Z0. Проекция имеет определенные конкретные параметры. При рассмотрении влияния одного из составляющих звеньев размерной цепи на величину замыкающего звена А?к можно видеть, что величина замыкающего звена увеличивается или уменьшается в зависимости от направления составляющих звеньев по отношению к замыкающему на величину проекции этого звена на замыкающее звено в базовой системе координат. Следовательно, номинальный размер замыкающего звена можно определить по формуле:

;

здесь Кi- — передаточное отношение звена цепи; n— число составляющих звеньев размерной цепи.

Для процедур моделирования реальной системы АСП необходимо расширить сущестсвую-щие методики в части возможности учёта случайных величин как погрешностей мсполнения сборочных операций, которые выполняются в определенных ранее заданных интервалах по заданным условиям и при заданных допусках на исполнительные размеры сборок. В связи с этим положение конца вектора Вi последнего звена цепи будет находиться в некоторой пространственной области, которая в пространстве сборки будет определяться конической фигурой, в основании которой лежит область рассеивания конца суммарного вектора в пространстве, а вершина конической фигуры находится в начале исходной системы координат. Образующие конической фигуры представляют собой предельные положения линий, определяющих фактическое направление замыкающего звена. Для определе- ния области рассеивания замыкающего звена необходимо определить ее проекцию на направление замыкающего звена, что позволит получать конкретные значения размеров замыкающих звеньев с учетом номинальных размеров составляющих звеньев и допусков на них.

Например, при сборке корневой нервюры кессона отъёмной части крыла в зоне соединения с корневой нервюрой центроплана нас будет интересовать расстояние между центрами базовых и рядовых отверстий разъёма. Для построения размерных связей необходимо определить расстояние А?к между двумя точками O1 и О2(рис.2), представленными соответствующими проекциями Ах1, Аy1 и Аz1и Ах2, Аy2, Аz2 в осях координат Ox, Оу, Oz с началом отсчета в точке О. Составляющими параметрами размерной цепи являются размеры, определяющие расстояние между проекциями сопрягаемых точек на оси Ох, Оу, Oz в системе координат XYZ. Для расчета величины искомого расстояния A?к1-2 звена А1 – А2 пространственной размерной цепи получим:

А _{Д к1} 2 =                                                 ( 1)

Составляющие параметры этой цепи выполняются с заданными допусками и могут иметь как наибольшие, так и наименьшие предельные значения. Поле рассеивания замыкающего звена представляет собой разность между наибольшим и наименьшим его предельными значениями:

^Ю А Д =         — .-._....           (2)

Подставив в (5) значения (Аmax – Аmin) вместо (А1- А2), учитывая значения задаваемых в граничных условиях величин A?прmax и A?прmin, определим с использованием теории размерных цепей величину поля рассеивания:

\ xlmax ж2тЁп/ 1 \ ylmax у2ттУ ' zlmax

ЮАД=  -М:;;- .<;_ ; " М:,. - л ?1,; ; - А:1;..... - А;?;,: ; ^

Анализ уравнения (7) показывает, что поле рассеивания замыкающего звена зависит от полей рассеивания составляющих параметров, а также от величин размеров этих звеньев, т. е.

m A_z1, m A_z2,^, m A_zk). (4)

Рассмотрим случай, когда при расчете пространственных размерных цепей необходимо обеспечивать минимальное значение величины замыкающего звена цепи, в том числе равное нулю (замыкающее звено как зазор в соединении трубопровода со штуцером агрегата, где минимальный зазор должен быть равным нулю, и др.).

A

Д пр min

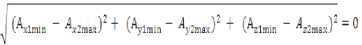
Для автоматизации процессов расчета раз- мерных связей в этом случае размерные цепи можно представить как графы размеров, где простым размерным цепям соответствуют простые циклы, вершинами являются поверхности, линии и точки, соединяемые размерами, а сами размеры – ребрами. При связанной размерной цепи граф размеров содержит не менее двух простых циклов. Каждому простому циклу, включающему в себя замыкающее звено размерной цепи, соответствует алгебраическое уравнение простой размерной цепи, а число таких уравнений при сложной структуре размерных связей равно числу простых циклов в графе размеров. Тогда условие рассеивания выполняется, если

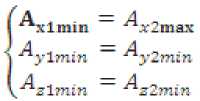
Тогда поле рассеивания замыкающего звена (8) определяется:

=

Значения xlmax

•1т ад

и        в урав- ур

нении (9) можно представить в следующем виде:

A      = A     4- T s xlmax     xlmin 1 xl

A      = A     4- T

■^■•Imax     ylmin 1 ylf

A = A 4- T zlmax zlmin 1 zl J где ,    ,    — допуски на размеры

,    . Аналогично получим:

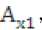
A      = A    — T

■^cZmax x2min 1 x2

A     — A    — T

A = A — T z2max z2min ¹ z2

где Tx2, Ty2, Tz2 — допуски на размеры Ax2, Ay2, Az2.

Заменив в (10) величины        ,, их значениями по (9), имеем: ,

A    = A—T x2min xlmin x2

A    = A

A = A —T z2min zlmin z2

Подставив значения (13) в (10) и произведя преобразования по условиям A? пр min = 0 найдем:

=                                          .(12)

Формулу (14) можно представить в общем виде для любого числа составляющих звеньев, заданных координатным способом при условии, что координаты составляющих векторов параллельны друг другу:

=                                          .(13)

Максимальное поле рассеивания замыкающего звена должно быть равно или меньше допустимого отклонения, тогда

=                                                .(14)

Согласно формулы (16) при        = 0 на правление замыкающего звена совпадает с диагональю суммарного параллелепипеда, который является областью рассеивания конца суммарного вектора замыкающего звена и максимально возможной величиной при различных сочетаниях допусков и размеров координат, что обеспечивает сходимость итерационных процессов достижения заданной точности построения размерных цепей.

Для определения граничных точек областей рассеивания составляющих векторов рассмотрим методику расчета области рассеивания для плоской размерной цепи. Предельные значения параметров можно найти по заданным отклонениям первых двух составляющих векторов, например, например, для параметра X — по формулам: Xmin = АХ + ЕLХ, Xmax = АХ + ЕSХ, где А — номинальное значение параметра х; Е Х — нижнее отклонение параметра х; ESX – верхнее отклонение параметра х. Для облегчения суммирования и возможности автоматизации расчетных работ нумерация вершины многоугольников, аппроксимирующих область, ведется против часовой стрелки (рис. 3)

В табл. 1 приведены сочетания параметров, определяющих область рассеивания составляющих векторов ai в первой четверти координат в зависимости от способа задания размерных цепей. Формулы для определения граничных точек векторов в прямоугольных и полярных координатах приведены в табл. 2

Вариации сочетаний предельных значений параметров позволяют формировать массивы областей рассеивания основных граничных точек областей. Для областей, заданных способами № 1, 3, 5, этих точек достаточно, чтобы оценить предельную область рассеивания составляющего вектора плоской размерной цепи, так как характер фигуры этих областей выпуклый. Для способов № 2, 4, 6 задания основных граничных точек области недостаточно, так как четыре граничные точки не дают полного представления о фигуре области. Например, для способа № 6 фактическая фигура области есть часть кольца.

Четыре граничные точки, соединяемые прямыми линиями, создают представление о фигуре в виде трапеции. Для способов № 2, 4, 6 на радиусных участках между основными точками производится аппроксимация участков окружности в зависимости от необходимой (заданной) точности расчета. Шаг аппроксимации А(р) определяется по формуле

\ф = 2arccos (1 — ), (15) где А — радиус дуги окружности; — стрелка прогиба.

Точность расчета определяется коэффициентом аппроксимации — отношением к допуску

Таблица 1. Сочетания параметров

Номер способа	Параметры				Г	раничные точки области с номерами
	а х	а у	l-4|		1	2	3	4
1	*	*			xmin, ymin	xmax, ymin	xmax, ymax	xmin , ymax
2	*		*		x min ,	x max ,	x max ,	x min ,
3	*			*	xmin,   min	х ГЛ - xmax,   min	х ГЛ xmax,   max	х - ГЛ xmin ,   max
4		*	*		y min ,	y max ,	y max ,	y min ,
5		*		*	y min,   min	y max,   min	y max,   max	y min,   max
6			*	*	1*^ 1 min> Фт1п	1^ 1 max >Ф min	1*^ 1 max >Ф max	1 ^ 1 min' Ф max

Таблица 2. Формулы для определения граничных точек векторов

Номер способа	Известные параметры вектора	Параметры вектора в прямоугольных координатах		Параметры вектора в поляр ных координатах
				Ai	*Pi
1	х>,У5	Xj	Yi	1 =      2	arctg (yi/xi)
2	ХрД				arccos (xi/Ai)
3	Xj-Vj	Xf	xi/tg i	x,/cos®	^i
4	У,.Й		Yi	A,	arcsin (yi/Ai)
5	У^Ф,	Yi/tgT,	Yi	Yi/sinv,	Vi
6	X	cos®	sin®	A:

Т на радиус окружности . Мера точности расчета

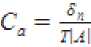
где Т = max- min. Минимальный угол аппроксимации Д ф = можно найти по формуле

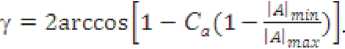
Для шестого способа задания области рассеивания составляющего вектора размерной цепи

координаты:

,        (18)

71 j I

,        (19)

где Аx, Аy— координаты конца вектора-номинала; ф — угол между вектором-номиналом и осью Ох; — минимальный угол аппроксимации.

За первую граничную точку области рассеи- вания принимается точка с минимальными значениями модуля вектора, т. е.

Таким образом получение окончательных размеров сборочной единицы приведено к процессам переноса размеров и форм, заданных графически в конструкторских чертежах, методами воспроизведения их в размерах и формах деталей и изделий с помощью технологической оснастки, оборудования и измерительных средств.

Окончательные размеры сборочных единиц самолетных конструкций зависят от видов погрешностей, накапливаемых в технологических переходах операций сборки в процессе производства, где функция дискретного перехода соответ- ствует содержанию задачи и адекватному переходу в модели системы автоматизированного проектирования технологических процессов (САПР ТП) сборки. Как показывает практика, распечатываемые в итоге карты технологических процессов являются достаточно достоверными по исходной информации в таких условиях, где модели непрерывных управляемых процессов представляются как дискретный по типовым переходам и операциям. Проблема заключается в правильном выборе и постановке задачи оптимизации для обеспечения полноты требуемого решения и его достаточной точности.

Если модель проекта сборки представить в виде общего графа сборочного пространства, то в областях допустимых вариаций параметров топологических схем размерных связей для взаимосвязанных процессов применимо рекуррентное уравнение Беллмана:

F - 1 ( X - i ) = max i ft ( X - 1 , X ( u j ) ) + F ( X ( u j ) ) } , i = ^1,2...., n , (21) где F - функция качества перехода, и F n ( X n ) = 0

Для обеспечения процесса шаговой оптими- зации ТП вводим ограничения на множество допустимых путей переходов состояний в виде дуг графа как множества решений соответствующих задач. Узлы, сгруппированные по уровням, соответствующим шагам переходов, образуют множества x0,x1,...,xN , где x0 и xN – адекватные конкретному узлу параметры, которые рассчитываются по специальным алгоритмам для исследуемых множеств. Такой подход является одним из эффективных путей решения задачи проектирования технологии сборки в виде модели как ориентированного графа.

В рамках решения соответствуюдщей задачи выбора оптимального по ряду критериев проекта ТП в работе рассматривается проблема определения, синтеза и оценки последовательности операторов преобразования сборочно-монтажного пространства. Так как сложная задача сборки и монтажа узлов и агрегата в целом подразумевает использование достаточно большого количества операций со специфическим набором инструмента и оснастки, которые должны быть не независимыми, а объединенными иерархически: некоторый оператор отражает факт принадлежности компонентов, рассматриваемых в задаче, конкретному множеству. Однако, сколько бы уровней рассмотрения ситуации ни понадобилось при решении поставленной задачи, отражения ее компонентов в виде высказываний, моделей и т.д., в конечном счете они сводят семантику логических высказываний от содержательной интерпретации моделей к констатации наличия определенных физических свойств у узла, агрегата, системы, а также выбора процесса сборки.

В задачах проектирования ТП необходимо совместить аналитическую взаимосвязь между параметрами уравнения и параметрами решения, одновременно с этим выразить эту взаимосвязь в виде алгоритма управляющих воздействий на системы разного рода. Таким образом, можно совместить в параметрическом виде исходное уравнение и его решение, получив параметрическую структуру, изменение которой с течением времени анализируется для получения оптимального параметрического пространства решений, в котором выбираются устойчивые состояния ТП. Тогда процессы оптимизации технологической системы (ТС) определят производственную стратегию сборочных процессов. В инвариантной ТС итерациональный процесс поиска экстремума связан с заданием соответствующих начальных условий в дифференциальных соотношениях, выражающих баланс основных процессов, причем параметрически изоморфных. Параметрический изоморфизм ведет к новым схемам классификации и описания конечномерных представлений. Тогда разложением в ряд базовой целевой функции по базисным век- торам получаем дискретные функции состояния ТС, причем коэффциенты разложения являются собственными значениями коэффициентов линейного оператора ( Ai, A2,..., An ), которым соответствуют вероятностные представления структуры узла, рассчитываемые как плотности вероятностей такого состояния. Изображение оригинала заданной вероятности в комплексной области может быть рассчитано как:

5 !

( p + A ) n ^{+ 1 ,} (2 2) где s – количество факторов и их выборочных значений в распределениях-композициях, р – комплексная величина; A — параметр-статистика, выражающий собственные значения линейных операторов,которые при преобразованиях технологического пространства сборки определяют инвариантность тензоров и тензорных функций относительно ортогональных преобразований пространства сборки.

Ортогональные тензоры Q: Е — л— — Е осуществляют повороты и зеркальные отображения, при этом они сохраняют длины векторов, углы между ними и переводят один ортонормирован-ный базис в другой. Определим понятие инвариантности тензора А: Е — л— — Е относительно ортогонального тензора Q: Е _—— л. _— Е .

Определение 1. Тензор А является инвариантным относительно тензора Q, если А удовлетворяет равенству :

А = Q о A о Q-1. (23)

Уточним геометрический смысл этого понятия. Пусть Q – ортогональный тензор, осуществляющий поворот любого вектора в пространстве E(dimE=3) на заданный угол вокруг оси, ортогональной плоскости чертежа сборки. Воспользуемся для наглядности искусственным построением образа пространства, в которое оператор Q: Е ———— Е переводит пространство Е, аналитически выражаемое разложением в ряд базовой целевой функции по базисным векторам. Обратный оператор Q-1 : Е —л—— Е возвращает про странство Е в исходное вследствие выполнения условия неразрывности преобразований. Пусть на пространстве Е задан тензор А: Е ———— Е. Найдем в производном пространстве Е такой тензор А : Е__л_— Е , который оказывал бы на любой вектор х g Е такое же действие, которое оказывает тензор А на прообраз вектора х (т.е. на вектор y = Q-1(x)) в пространстве Е. Искомый тензор д должен удовлетворять выбранной схеме сборки по соотношению: Vx Е Е А(х) = Q(A(y)) = Q(A(Q-1 (x))) , которое эквивалентно тензорному равенству

А = Q о A о Q-1.          (24)

Отождествим векторные пространства Е и Е~ таким образом. что в результате (23) переходит в ортогональный тензор Q, относительно которого тензор А инвариантен и является симметрией тензора А. Понятие инвариантности тензора А относительно ортогонального тензора Q может быть обобщено и на аналогичные тензорные функции, отображающие преобразование сборочного пространства по варьируемым размерным цепям. Таким образом, предложен метод, с помощью которого в исчислении последовательности операторов преобразования возможно решать задачи высших порядков в рамках логики построения размерных цепей, в том числе и с точки зрения математической логики в виде построения n-местных предикатов с варьируемым числом функциональных звеньев размерных цепей.