Методика бесконтактного диагностирования топологии вмятин на нефтеналивных резервуарах

МЕТОДИКА БЕСКОНТАКТНОГО ДИАГНОСТИРОВАНИЯ ТОПОЛОГИИ ВМЯТИН НА НЕФТЕНАЛИВНЫХ РЕЗЕРВУАРАХ

Предложена методика сеточного замера глубины вмятин на стенках вертикальных цилиндрических резервуаров с использованием программируемого монохромного лазерного луча. Получены соотношения для определения координат точек пересечения трехмерных кривых линий по их двумерной аксонометрической проекции и минимальному числу исходных данных. Алгоритм использован для определения топологии вмятины по ее «фотографии». Проанализирована погрешность метода по результатам его апробации на компьютерных моделях реальных вмятин.

Одним из наиболее часто встречающихся типов дефектов, возникающих при монтаже и эксплуатации вертикальных стальных цилиндрических резервуаров, являются вмятины и выпучины. Их происхождение носит разный характер, например сварные напряжения, неравномерная усадка основания, потеря устойчивости и т.д. Естественно, что они бывают разных форм и размеров. В действующих нормативах [1]

источник монохромного света

Рис. 1. Схема эксперимента

используются только два параметра, по которым определяются недопустимые вмятины: расстояние от нижнего до верхнего края вмятины (т.е. высота) и стрела прогиба. При этом не учитываются такие немаловажные параметры, как толщина стенки, относительная ширина (отношение ширины вмятины к ее высоте), высота нижнего края вмятины над окрайкой и др. В то же время опыт эксплуатации резервуаров свидетельствует об отсутствии влияния большинства дефектов, подлежащих устранению согласно существующим нормам, на надежность и долговечность конструкции. В связи с этим разрабатывается новая уточненная методика [2] оценки напряженного состояния в зоне дефекта с использованием численных методов, а именно МКЭ.

Описание метода. Для ускорения процесса диагностирования вмятин при техническом обследовании предлагается новая технология. Она позволяет построить достаточно достоверную картину изменения глубины по всей области дефекта. Это может быть использовано для усовершенствования методики, описанной в [2–4]. Кроме

того, метод позволяет исключить высотные работы персонала при ручном измерении высоко расположенных вмятин, уменьшить время обследования, а также, имея построенную по результатам замеров модель, автоматизировать процесс проверки вмятин на их допустимость.

На участок стенки резервуара с локальным несовершенством формы с помощью программируемой системы лучей монохромного (по умолчанию – красного цвета) лазера проецируется сетка (рис. 1). При этом граница дефекта целиком оказывается внутри границ разлинованной области. Цвет лазера должен контрастировать с окраской самой стенки резервуара, надписей на ней или каких-либо других объектов, оказывающихся внутри или около зоны проекции.

Параметрами в данном случае будут радиус резервуара, расстояние от проецирующего устройства до стенки резервуара без дефекта (либо до центра резервуара), углы развертки а1, а2 - углы между крайними горизонтальными или вертикальными лучами, а также размерности сетки m и n. Угол между двумя ближайшими лучами будет составлять а1 /т и а2/и соответственно.

Очевидно, что при проецировании системы лучей на плоскость из некоторого управляемого прямолинейного источника света (лазер) результирующая сетка не будет равномерной. По рис. 2 определяем:

h1 = L ■ tga;

h 2 = L ■ tg(2 a ) - h 1 =

2tg a v ¹ - tg² a

^

- tg a L = к ■ L ■ tg a , J

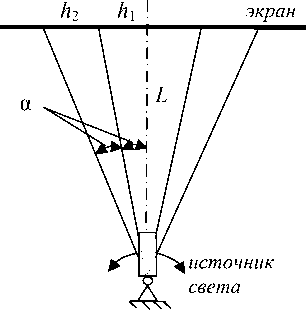
Рис. 2. Неравномерность шага сетки

где к =

1 + tg2a

1 - tg2a

- коэффициент увеличения шага сетки к краям проекции, к >  1.

Так как угол а достаточно мал, то увеличение размера ячеек сетки незначительно, но если не учитывать этот эффект, то это приведет к увеличению погрешности. В еще большей степени этот эффект будет проявляться при использовании в качестве экрана цилиндрической оболочки. Причем неравномерность шага сетки, а соответственно, и углов будет тем значительней проявляться, чем больше радиус кривизны. Кроме того, горизонтальные проецируемые линии сетки в действительности не будут таковыми. В данной работе модели вмятин строятся по результатам инструментальных замеров с равномерным шагом через 100 мм, поэтому вышеописанные эффекты не учитываются.

Участок стенки резервуара, на который спроецирована решетка, фотографируется под достаточно острым углом с помощью цифрового фотоаппарата. Это делается таким образом, чтобы на фотографии было отчетливо видно изменение кривизны линий изначально правильной решетки в зоне дефекта. Для минимизации ошибки потребуется запечатлеть участок стенки с дефектом с двух сторон. Надежнее запечатлеть решетку с 2–3 ракурсов, в итоге результаты можно будет усреднить. Фотография по возможности должна иметь большое разрешение, а изображение решетки занимать как можно большую часть в видоискателе, при этом полностью в нем помещаться. Этим обеспечивается непрерывность растрового изображения решетки. Кроме того, увеличивается ширина растровых линий, что, во-первых уменьшает погрешность определения узловых точек в нижеописанном алгоритме, а во-вторых уменьшает вероятность значительного искажения цветовой палитры при сжатии растрового изображения в тот или иной формат графических данных. Наиболее часто используется алгоритм сжатия изображений JPEG, но нет никаких ограничений на использование других форматов, которые обеспечивают приемлемое качество.

Поиск узловых точек . Скелетизация растрового изображения . Полученное цифровое изображение сетки необходимо представить в векторном виде с использованием графа. Для этого

• а)    изначальное цветное изображение (фотография) преобразуется в бинарное растровое – двумерную матрицу из черных и белых точек, в которой объект задается черными точками растра (1), а фон – белыми точками (0). При этом в качестве объекта выбираются пиксели из некоторого достаточно узкого интервала цветовой палитры. Этот интервал необходимо задавать таким образом, чтобы объект по возможности состоял только из пикселей, принадлежащих линиям монохромной проецируемой сетки. Для этого может потребоваться обработка начальной фотографии в каком-либо графическом редакторе. Результирующее монохромное изображение должно быть непрерывным и по возможности без большого шума по границам линий;

• б)    определяется первоначальный скелет растрового изображения. Существует несколько традиционных методов построения непрерывного скелета [5], но они либо громоздки, либо сложны для реализации, либо имеют побочные эффекты, ограничивающие их применение. В настоящей работе используется волновой алгоритм [6], оптимизированный под данную задачу;

• в)    оптимизируется первоначальный скелет. Отбрасываются шумовые узлы, а узлы, лежащие в некотором доверительном интервале (зависит от средней ширины линий), объединяются. В итоге получаем окончательный граф, представляющий собой массив с координатами узлов и матрицу смежности. Число оставшихся узловых точек должно быть равно m×n ;

• г)    по результирующему графу узлы, соответствующие одной горизонтальной или вертикальной линии сетки, компонуются в определенные структуры.

Преобразование     координат .

Определение глубины вмятины . В качестве исходных данных для следующего этапа используются:

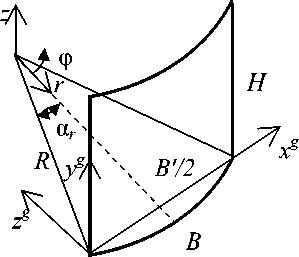
Рис. 3. Системы координат трехмерной модели сетки и ее плоской проекции

• 1)    радиус резервуара R ;

• 2)    пространственные коо рдин аты точек     ( x_i ^g , y_i ^g , z_i ^g ),

i = 1,2 m , принадлежащих крайним горизонтальным дугообразным линиям. Определяются по габаритным размерам, которые, в свою очередь, определяются по числу вертикальных и горизонтальных линий ( m и n соответственно) и известным шагам между ними ( h x и h y );

• 3)    прое кцио нные координаты этих же точек на плоском изображении ( x ^р , y^p ), i = 1,2 m .

Кроме ЦСК ( r ф z ) , в которой удобно вести построение модели сетки, введем две системы координат, как показано на рис. 3: трехмерную (пространственную) СК, связанную с габаритными точками, и двумерную (проекционную). Пусть начало первой расположено в левом нижнем узле трехмерной модели сетки с координатами ( x 1 g , y 1 g , z 1 g ) = (0,0,0) (см. рис. 3). Ось x g направлена к правому нижнему узлу

( x 2 mg , У 2 mg , z 2 mg ) = ( ⁵ ',0,0), а ось y ^g - к левому верхнему ( x_{m + 1} ^g , y_{m + 1} ^g , z_{m + 1} ^g )

= (0, H, 0). Здесь B' = 2R sin ar. Проекционная СК соответствует двумерному образу сетки, отсчет ведется с левого нижнего угла изображения.

Преобразование пространственных координат в проекционные происходит при аксонометрической проекции в следующей последовательности:

1. Повороты вокруг осей: xg (угол a), у' (угол в), z'' (угол у), где штрихом обозначена ось после поворота на a, а двумя - на a и в . Соответствующие матрицы поворота A , B и G записываются следующим образом:

	Г 1	0	0	0 "		cos в	0	- sin в	0 "		cos y	- sin y	0	0 "
	0	cos a	- sin a	0		0	1	0	0		sin y	cos Y	0	0
A =					, B =	sin в		cos в		, G =
	0	sin a	cos a	0			0		0		0	0	1	0
	. 0	0	0	1 _		. 0	0	0	1 _		. 0	0	0	1 _
В итоге		получаем координаты x				, y ,	z ''':

{ X ," У ,- z ," 1 } T = P { x , У , z , 1 } T ,

где

P = G • B • A =

cos в cos Y - sin a sin в cos Y— cos a sin Y - cos a sin в cos Y+ sin a sin Y 0

cos в sin y - sin a sin в sin y+ cos в cos Y - cos a sin в sin y- sin a cos y 0

sin в              sin a cos в                    cos a cos в            0

0                     0                               0                 1

С этого момента координата z не важна.

2. Смещения в плоскости x ''' y ''' повернутой системы координат на dx, dy для совмещения координат. Обеспечим совпадение первой точки x1 ''', y1 ''' с ее проекцией x1p, y1p , тогда

Г1 0 0 dx Г1 0 0 x1p" D = 0 1 0 dy = 0 1 0 У1p 0 0 1 0 0 0 1 0 .0 0 0 1 _ .0 0 0 1 _ и в итоге

{ X , У , z , 1 } T = D { x ," У Г z ," 1 } T •

• 3.    Масштабирование (растяжение или сжатие) с коэффициентом k в плоскости x ^d y ^d для окончательного преобразования в координаты x_i ^p , y_i ^p . Матрица

масштабирования K с учетов равенства коэффициентов сжатия по осям выглядит следующим образом:

k_x 0 0 0

k 000

0 k 00

00 k 0

0 k_y 0 0

0 0 k_z 0 0001

В итоге для i -й точки получим следующую матричную зависимость преобразования из одной СК в другую:

где C = K ■ D ■ G ■ B ■ A . В формуле (1) отброшена за ненадобностью координата zi^p .

Требуется по двумерному изображению сетки m х n линий определить координату z_i ^g всех ее узлов. Для этого необходимо решить задачу, обратную (1). При решении обратной задачи неизвестными являются: а , в , у , к . По условиям задачи граничные линии точно повторяют форму неискаженного цилиндра без дефекта, т.е. координата r i — R (в ЦСК) для всех крайних узловых точек. Поэтому координаты

{xyrast, vjas} образов этих точек, полученные по растровому изображению, должны совпадать с координатами {xyp, yyp}, полученными по формуле (1). Используя это условие, поиск неизвестных будем вести методом минимизации невязки. Невязка строится для всех точек, лежащих на крайних дугообразных линиях (j — 1 и j — n).

Запишем функционал в виде nn

J ^— Е S i ,1 ⁺ Е S i , n —^> min,                      (2)

i 1 i 1

p rast 2 p rast 2 p p где Si j — (Xjj Xjj ) +(У jj У jj ) ; {Xjj ; Уу j проекционные координаты образа узла, лежащего на пересечении i-й горизонтальной и j-й вертикальной линий; {Xjjp; yijP } - действительные координаты этого же узла на изображении.

Функционал (2) имеет две точки устойчивого минимума, отличающиеся знаком значений углов поворота а и в (вокруг осей x g и y g соответственно). Одна из этих точек соответствует обратной кривизне цилиндра, то есть точка обзора находится как бы внутри цилиндра. И в зависимости от начального приближения получаем один из этих минимумов, а после нахождения обеих экстремальных точек легко выделить верное решение, когда направление обзора соответствует действительному.

После решения задачи (2) и определения четырех неизвестных величин можно по (1) получить проекционную координату любой точки, лежащей на поверхности цилиндра известного радиуса, и наоборот.

Остается последний шаг – расчет расстояния (глубины) от идеальной точки на поверхности цилиндра без дефекта до реального ее расположения в зоне вмятины по образу этого расстояния на фотографии. Для этого используем обратное решение системы (1):

x i^g y i^g z_i ^g

• = C-i<

. Xip . _ yip

или

g   V.   +^yybr = ij      k (P13 + P23)

p rast p rast

(xj - xti   ) + (yti - yti   )

k ( - cos a sin P (cos у+ sin y ) + sin a (sin у - cos y ) )

Рис. 4. «Фотография» вмятины: углы поворота: a = 17,2 ^o , p = 49,7 o , y = 13,3 ^o

Таким образом, имея минимальное число исходных данных, по двумерному образу сетки можно восстановить ее трехмерное изображение и, главное, величины прогибов в зоне вмятины. С учетом перспективы, что, конечно же, будет наблюдаться на реальных фотографиях, формулы перехода усложняются, но принцип остается тот же.

Апробация    методики.    Для проверки предложенного метода использовались результаты замера топологии нескольких вмятин на резервуаре УППН «Кокуй», ЦДНГ-10, ООО «ЛУКОЙЛ-ПЕРМЬ», РВС № 3 [3]. Построена компьютерная трехмерная модель вмятины №3 (результаты замеров глубины представлены в табл. 1), по которой получены 6 различных проекций («фотографий»), сохраненные затем в формат JPEG. Углы в каждой проекции получались с условием, что на картинке достаточно отчетливо прослеживается кривизна линий в зоне дефекта. На рис. 4 представлена часть изображения одной из таких «фотографий». Разрешение всех картинок составляет 1024х726 пикселей, тогда как изображение занимает большую часть по высоте и примерно 1/3 часть – по ширине. Средняя ширина линий – 4 пикселя.

После обработки изображений с использованием вышеописанной методики получены 6 таблиц с сеточными значениями глубин вмятины. Максимальная абсолютная ошибка по всем ячейкам таблиц в сравнении с реальными величинами составляет порядка 15 мм. Стоит упомянуть, что значение стрелы прогиба реальной вмятины равно 30 мм. На трех из шести фотографии погрешность менее 6 мм. При этом в точке максимального прогиба ошибка обычно не превышала 10 %. Большая погрешность в некоторых точках (до 15 мм) связана в основном с работой волнового алгоритма распознавания точек пересечения дискретных растровых линий, а именно их последующего уточнения. Уточненные координаты этих точек отличаются от их визуально предполагаемого месторасположения всего лишь на 2–4 пикселя. Такие ситуации носят случайный характер и часто неизбежны в силу дискретности изображений и потери, при кодировании / декодировании в формат JPEG, части информации об изображении.

Таблица 1

Вмятина № 3. Глубина вмятины в точках сетки, построенной с шагом 100 мм

0	2	0	0	3	5	3	2	0	0	0	0	0
0	4	4	5	7	10	7	5	5	5	3	0	0
0	6	8	10	12	15	15	15	14	14	10	8	2
0	8	11	15	17	22	20	20	20	20	16	12	3
0	10	15	20	22	25	25	25	25	25	20	17	3
0	10	15	20	22	25	25	25	25	25	20	18	3
0	7	13	20	20	20	23	25	27	30	25	18	3
3	4	8	15	15	15	19	22	25	25	20	18	3
2	4	7	10	12	15	15	14	12	12	12	13	3
0	3	5	7	8	10	10	10	8	6	6	5	2
0	2	3	4	4	5	5	5	3	3	3	3	0
0	0	0	2	2	3	3	3	2	0	0	0	0

Минимизировать случайные погрешности позволяет процедура осреднения результатов. После осреднения всех сеточных значений и зануления отрицательных величин прогибов (которые не превышали 2 мм) по полученным шести таблицам (табл. 2) максимальная абсолютная ошибка стала меньше 3 мм (табл. 3), а погрешность по стреле прогиба составила всего 1 мм (31 мм вместо 30) или 3,3 %.

Таблица 2

Сеточные значения глубины вмятины, полученные после процедуры осреднения

1	2	0	0		4	8	5	4	2	1	2	2	1
1	5	4	6		8	12	8	6	5	6	3	0	2
1	6	7	11		13	16	16	15	15	16	10	10	3
0	8	11	16		17	22	19	20	22	20	17	13	5
1	11	14	19		23	24	25	25	24	25	20	18	5
0	10	15	21		23	25	24	25	25	26	20	19	4
1	8	12	20		19	20	23	25	28	31	25	19	4
3	4	8	16		15	17	18	23	25	25	19	20	4
1	3	7	11		13	16	15	14	13	14	13	14	4
3	2	4	7		7	10	9	10	7	6	5	6	2
1	2	3	4		4	5	5	5	2	4	3	3	1
1	1	0	2		1	3	3	3	2	0	1	1	0

Таблица 3

Абсолютная погрешность методики для вмятины № 3

Рассмотрим применение полученных сеточных значений глубины вмятины при

расчете местных упругих напряжений на

909Е+07           . 728Е+08           .137Е+09           .200Е+09              .275Е+09

. 409Е+08           .105Е+09           .168Е+09           .232Е+09

Рис. 5. Вмятина № 3. Картина распределения эквивалентных напряжений, Па

участке стенки резервуара с дефектом. Проводился анализ напряженного состояния резервуара по методике, изложенной в [2–3], с учетом геометрической нелинейности при предельной высоте взлива продукта для реальной вмятины (см. табл.1) и для вмятины, топология которой получена по вышеописанной технологии (см. табл. 2). По результатам расчетов невязка по эквивалентным напряжениям составляет около 13,5 %, так как в первом случае (для реальной вмятины) максимальные напряжения равны 238 МПа, а во втором – 275 МПа (рис. 5), при этом качественно картины напряжений совпадают.

1	0	0	0	1	3	2	2	2	1	2	2	1
1	1	0	1	1	2	1	1	0	1	0	0	2
1	0	1	1	1	1	1	1	1	2	0	2	1
0	0	0	1	0	0	1	1	2	0	1	1	2
1	1	1	1	1	1	0	0	1	0	0	1	2
0	0	0	1	1	0	1	1	0	1	0	1	1
1	1	1	0	1	0	0	0	1	1	0	1	1
1	0	0	1	0	2	1	1	0	0	1	2	1
1	1	0	1	1	1	0	0	1	2	1	1	1
3	1	1	0	1	0	1	0	1	0	1	1	0
1	0	0	0	0	0	0	0	1	1	0	0	1
1	1	0	0	1	0	0	0	0	0	1	1	0

Заключение . Таким образом, можно утверждать, что построение трехмерной модели вмятины на резервуаре по ее нескольким фотографиям вполне возможно. При этом погрешность по максимальному значению стрелы прогиба составляет всего несколько процентов. В дальнейшем необходимо отладить работу алгоритма для распознавания сетки на реальных фотографиях. Кроме того, все разрешающие соотношения нужно будет использовать с учетом перспективности изображений на реальных фотографиях.

Описанную методику можно использовать для оценки технического состояния резервуара с вмятинами при их ежегодном диагностировании. При этом можно использовать как упрощенный инженерный подход, руководствуясь существующими нормативами и правилами (потребуется только значение стрелы прогиба), так и полностью анализировать НДС вмятины с использованием любого конечно- элементного пакета (например, ANSYS). В последнем случае анализ можно проводить с учетом большого числа геометрических параметров вмятины, а также с учетом геометрической и физической нелинейности.