Методика численного расчета оптимальных форм тел вращения при движении в грунтовой среде
Автор: Баженов В.Г., Котов В.Л., Линник Е.Ю.
Статья в выпуске: 2, 2015 года.
Бесплатный доступ
Разработана методика расчета оптимальных форм осесимметричных ударников при движении в грунтовой среде на основе прямого оптимизационного метода с применением методов локальных вариаций и циклического покоординатного спуска. Прямые численные расчеты проводятся в осесимметричной постановке. В качестве начального приближения принимается форма тела, найденная на основе модели локального взаимодействия. Используемая модель локального взаимодействия (МЛВ) основана на аналитическом решении одномерной задачи о расширении сферической полости в грунтовой среде Григоряна при допущении несжимаемости среды за фронтом ударной волны. Ранее теоретически и экспериментально были обоснованы главные допущения при решении задачи оптимизации формы осесимметричных тел в рамках МЛВ: квадратичная по скорости модель применима, трение пропорционально давлению, обтекание безотрывно. Сравнением с результатами численных расчетов в осесимметричной постановке на основе модели грунтовой среды Григоряна показана применимость МЛВ к описанию проникания острых конусов и ее погрешности в определении сил сопротивления применительно к затупленным телам. В данной статье эффективность разработанной методики демонстрируется на примере задачи определения формы ударника, минимального сопротивления внедрению в среду тел вращения заданной длины и радиуса поперечного сечения. Показано хорошее соответствие результатов при задании образующей тела вращения в форме параметрического полинома Безье и кусочно-линейной кривой. Исследованы сходимость последовательных приближений при численном решении задачи параметрической оптимизации и погрешность определения силы сопротивления в зависимости от величины вариации параметров образующей. Выявлена существенная роль двумерных эффектов обтекания.
Проникание, грунтовая среда, минимальное сопротивление, полином безье, безусловная параметрическая оптимизация, модель локального взаимодействия, метод локальных вариаций
Короткий адрес: https://sciup.org/146211562
IDR: 146211562 | УДК: 539.3 | DOI: 10.15593/perm.mech/2015.2.01
Текст научной статьи Методика численного расчета оптимальных форм тел вращения при движении в грунтовой среде
PNRPU MECHANICS BULLETIN
Разработка методов построения форм тел, оптимальных по сопротивлению и/или глубине проникания в общей постановке, возможна лишь при наличии упрощающих предположений о характере взаимодействия тела и среды [1–3], например гипотезы локальности [4–9]. В основе получивших широкое распространение [9–14] моделей локального взаимодействия (МЛВ) лежит предположение, что каждый элемент контактной поверхности взаимодействует со средой независимо от других участков тела. Применение различных модификаций МЛВ позволило выделить [9, 15–18] класс абсолютно оптимальных тел (АОТ), содержащий общее решение достаточно широкого круга задач оптимизации формы тела, проникающего в грунтовые среды. В пространственной постановке нормаль к поверхности таких тел составляет с направлением движения постоянный оптимальный угол [15]. Среди тел вращения АОТ является круговой конус с тем же оптимальным углом раствора, определяемым скоростью тела и прочностными характеристиками среды. Для грунтов малой прочности осесимметричные АОТ обладают значительным удлинением. Для поиска формы тела вращения минимального сопротивления внедрению при заданной длине тела, меньшей длины абсолютно оптимального конуса, которая, как известно, содержит торец [16], необходимо применять численные методы [19].
Известные методы решения задач поиска образующей тел с притуплением, внедряющихся на максимальную глубину, основаны на использовании МЛВ. Постановка и численный метод решения вариационных задач на основе генетического алгоритма изложен в работе [19], разработке модификаций метода локальных вариаций посвящены работы [20, 21], где рассматривались задачи проникания оптимальных тел с торцом в среды типа металла или бетона. Для грунтовых сред экспериментально и теоретически – сравнением с результатами численных расчетов в осесимметричной постановке на основе модели грунтовой среды Григоряна – была показана применимость МЛВ к описанию проникания острых конусов [22–23]. Погрешность МЛВ на базе решения задачи о расширении сферической полости в определении сил сопротивления внедрению затупленных тел исследована в работах [14, 23]. Показано (на примере задачи поиска оптимального тела вращения заданной длины и площади основания) [6], что решение с учетом нелинейных эффектов обтекания в двумерной постановке позволяет существенно уточнить как форму, так и силовые, и кинематические характеристики оптимальных затупленных тел при проникании в грунтовые среды.
В данной статье аналогично [24, 25] сила сопротивления внедрению в грунт – целевая функция в задаче оптимизации формы тела, определяется на базе упрощенной модели контактного взаимодействия при различных параметризациях образующей [26–28]. Далее полученное решение принимается в качестве начального приближения в итерационном процессе построения оптимальной формы ударника при движении в грунтовых средах на основе численных расчетов в осесимметричной постановке.
1. Постановка задачи и методика численного решения
Рассматривается стадия развитого проникания ударника при постоянной скорости внедрения V0, причем обтекание искомой головной части ударника грунтом плотностью ρ0 происходит безотрывно. Введем цилиндрическую систему координат r0z, 0z – ось симметрии. Ударник – тело вращения заданной длины L с радиусом основания R, образующая боковой поверхности тела описывается кривой r(z) и включает передний торец радиусом R0. Действующее контактное давление определяется только нормальной компонентой вектора скорости в соответствии с МЛВ общего вида с = p0V02 f (а), а = sin П, где η – угол, образованный направлением вектора скорости и касательной к искомой кривой r(z).
Полное осевое сопротивление F проникающего тела вращения [19, 27, 28] с плоским R
передним торцом имеет вид F = с 0 R , + 2 п j с rdr . Положим D = F, ( p 0 V 0 2 S ) , S = п R 2
–
R 0
площадь миделя; r 0 = R 0/ R - радиус притупления; l = L/R - удлинение тела, тогда
D [ r ( z ) ] = f ( 1 ) r + 2 j f ( а ) rdr .
r 0
Таким образом, при известной функции f (а) имеем простейшую задачу вариационного исчисления, в которой необходимо определить такую выпуклую кривую r (z), удовлетворяющую условию r (l) = 1, что полное сопротивление (1) имеет минимум. При- ближенное решение этой задачи на основе известного метода локальных вариаций [29] сводится к отысканию чисел, минимизирующих функцию Nпеременных D(r0,r1,...,rN-1), где (r0,r1,...,rN-1) - искомые точки кусочно-линейной аппроксимации кривой при известном соответствующем распределении координат(0,z1,...,zN-1) (см. также [20, 21]).
Ранее была показана [28] сходимость последовательных приближений при кусочнолинейном представлении образующей боковой поверхности оптимального тела и убывание погрешности определения силы сопротивления с ростом числа узлов образующей. В задачах газовой и аэродинамики доказана эффективность аппроксимации образующей в классе полиномов или степенных функций, содержащих небольшое число искомых параметров оптимизации [26]. Отмечено [27], что аппроксимация квадратичным полиномом в форме Безье является удачной параметризацией образующей оптимального тела и в случае проникания его в грунт. Модифицированный алгоритм [27, 28] позволяет единообразно проводить вычисления как при кусочно-линейном представлении образующей, так и при функциональном, когда компоненты вектора ( r 0,..., rN - 1 ) являются параметрами полинома. Для применения алгоритма необходимо конкретизировать способ расчета интегральной силы сопротивления внедрению D в соотношении (1) - на основе МЛВ или одной из известных моделей грунтовой среды в постановке механики сплошных сред [14, 23].
Вектор неизвестных параметров r = { r i } , i = 0, N - 1, является одним из локальных экстремумов (1), для определения которых составляется система уравнений
D '( r ) = 0, о
aD a ri
> = 0, i = 0, N - 1.
Система нелинейных уравнений (2) решается итерационным методом Ньютона:
D ''( r k ) (rk+7 - r k ) = -D '( r k ), о
a 2
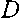
a r i a r
k
A r j + 1
k ad -s — ^
a r i
i , j = 0, N - 1,
где k - номер итерации; D ''( rk ) - симметричная матрица коэффициентов (в случае кусочно-линейного представления образующей имеет трехдиагональный вид). Частные производные первого и второго порядка могут вычисляться точно или методом конечных разностей с шагом варьирования 5 [27, 28].
Проведение вычислений на каждой итерации (3) эквивалентно нахождению минимума приращения сопротивления A D , представленного в виде квадратичной формы разложением в ряд Тейлора в окрестности Г :
N -1 Л Г)
A D VD A rk + 1
^ a r i i
1 N - 1 a 2 d +-
2 ^ о a r i a r j
A rk + 1 A r j + 1 .
Другие полиномиальные интерполяции целевой функции в области изменения параметров радиусом 5 могут быть получены методами планирования эксперимента [30]. Наиболее полная модель, основанная на полном ортогональном плане второго порядка, включает все промежуточные взаимодействия факторов, но требует для реализации проведения N 3 вычислений целевой функции и при больших N является, очевидно, избыточной. В ротатабельных планах второго порядка число расчетов не меньше чем
N 2 + 2 N + 1. Для вычисления коэффициентов (4) на основе центральных разностей второго порядка аппроксимации также может быть составлена матрица планирования, количество операций равно N ( N - 1 ) + 2 N + 1. Существенно уменьшить количество параметров N , как было отмечено выше, позволяет представление образующей оптимального тела кривой Безье [31].
Параметрический полином в форме Безье описывается выражением
P ( 5 ) = (1 - 5 )2 Р о ( 5 ) + 2(1 - 5 ) SP 1 ( 5 ) + S 2 Р 2 ( S ) , S G [0,1]. (5)
С учетом поставленных ограничений - заданных безразмерных величин радиуса основания и длины искомого оптимального тела r2 = 1, z о = 0, z 2 = l , вектор параметров r содержит три параметра ( N = 3), представляющих неизвестные координаты вершин P i , i = 0, N - 1, характеристического треугольника полинома Безье (рис. 1), ф 0 и ф 2 - углы при соответствующих вершинах характеристического треугольника.
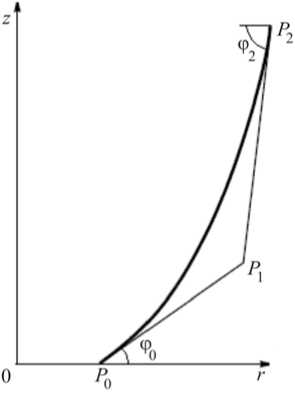
Рис. 1. Представление образующей параметрическим полиномом Безье
Таким образом, на каждой итерации метода Ньютона (3) целевую функцию необходимо вычислять 15 раз. Это не критично при аналитическом вычислении функции, но существенно увеличивает трудоемкость при численном расчете обтекания ударника даже в осесимметричной постановке.
В данной работе аналогично [24] предварительное исследование точности и сходимости методов оптимизации формы ударника, обоснование выбора приемлемой аппроксимации образующей проводятся в упрощенной постановке на основе МЛВ. Как будет показано да- лее, решение задачи параметрической оптимизации методом циклического покоординатного спуска с изменением шага варьирования 5 позволит уменьшить число вычислений.
2. Результаты предварительных расчетов
В качестве тестовой рассмотрим задачу проникания в грунт, поведение которого описывается моделью нелинейно-сжимаемой жидкости. Как было показано ранее [14], в этом случае реализуется наибольшая ошибка МЛВ при определении силы сопротивления внедрению. Сжимаемость грунтовой среды характеризуется ударной адиабатой:
c = A + Xи,
представленной линейной зависимостью скорости ударной волны с от массовой скорости и за ее фронтом. Постоянная А характеризует скорость распространения волны сжатия в грунте при малых давлениях, X - предельную сжимаемость грунта.
Численные расчеты проводятся при следующих значениях параметров: А = 460 м/с; X = 2,3; р0 = 1700 кг/м3, размеры тела R = 0,01 м; L/R = V5, скорость прони кания V0 = 400 м/с.
Поведение нелинейно-сжимаемой жидкости описывается одночленной МЛВ f ( а ) = C а 2. Среднее значение константы С , определенной из решения одномерной задачи о расширении сферической полости [3, 14, 32-34],
3/2 — е — е 4 Vo а , 1/з ,
C = —-----з—, е = -°—, c = Х /3 С0а + A /3, 1 — е3 c при а2 = 1/6 примем равным С * 1,1.
На рис. 2 приведены результаты расчетов оптимальных форм: кривые 1 есть численные решения системы уравнений (3) на основе МЛВ, кривые 2 получены в осесиметрич-ных численных расчетах (см. далее). Светлые квадраты соответствуют кусочнолинейному представлению образующей ( N = 16), сплошная и штриховая линии 1 - представлению образующей в форме полинома Безье при N = 3 и 2. Видно, что решение, определяемое тремя параметрами, практически точно соответствует кусочно-линейному представлению (фрагмент в окрестности вершины тела см. на рис. 2).
Пунктирная линия также является решением системы (3) при N = 3 и получена в сходящемся итерационном процессе метода Ньютона, но при другом начальном приближении. Из двух решений локальному минимуму соответствует только образующая, изображенная сплошной линией (все угловые миноры матрицы вторых производных D '' в соотношениях (3) положительны). Другое численное решение, локальным минимумом не является - угловые миноры матрицы D '' имеют разные знаки, и значение силы сопротивления для него несколько больше.
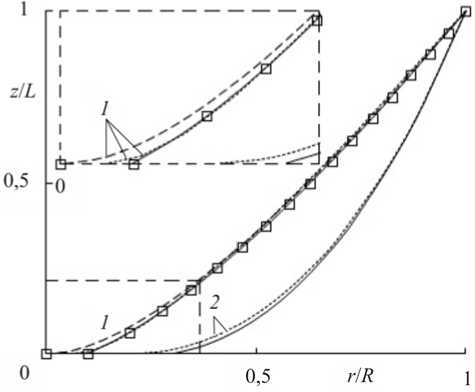
Рис. 2. Образующие оптимальных тел вращения
Параметры решений приведены в табл. 1, жирным шрифтом выделены искомые параметры полинома Безье.
Таблица 1
Параметры оптимального тела в рамках МЛВ
|
N |
P о ( r , z ) |
P 1 ( r , z ) |
P 2 ( Г , Z ) |
Ф 0 |
Ф 2 |
D |
|
3 |
( 0,096 ; 0) |
( 0,419 ; 0,356 ) |
(1; 2,236) |
0,834 |
1,271 |
0,1485 |
|
3 |
( 0,061 ; 0) |
( 0,280 ; 0 ) |
(1; 2,236) |
0 |
1,259 |
0,1494 |
|
2 |
(0; 0) |
( 0,298 ; 0 ) |
(1; 2,236) |
0 |
1,267 |
0,1507 |
*
Обозначим оптимальные значения в первой строчке табл. 1 верхним индексом
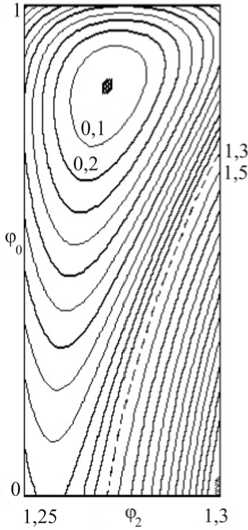
(r* = 0,096, .„, D* = 0,1485). На рис. 3 представлены линии равного уровня целевой функции 5D = | -^- -1 1100, полученные при фиксированных значениях радиуса притуп-ID * / ления r0 = 0,046; 0,052 и r0* =0,096. Углы ф0 и ф2 принимают значения в интервалах [0; 1] и [1,25; 1,3] соответственно. Изолинии даны с шагом 5D = 0,03 до значения 5D = 1,02 (штриховая линия на рис. 3, а, б) и с шагом 5D =0,2 при 5D>1,02; на рис. 3, в используется шаг 0,1 до значения 5D=1,3 и вдвое больший при 5D >1,3, штриховая линия также соответствует линии раздела. Видно, что при r0 « 0,052 функция 5D по пере менным ф0 и ф2 имеет два минимума: краевой и локальный (см. рис. 3, б). При r0 = 0,046 имеется только краевой минимум при ф0 = 0 (см. рис. 3, а), при r0 = r0* достигает- ся только локальный минимум (см. рис. 3, в), являющийся также и глобальным. Отметим также, что минимум по переменной ф2 может быть локализован лишь при 5< 0,01.
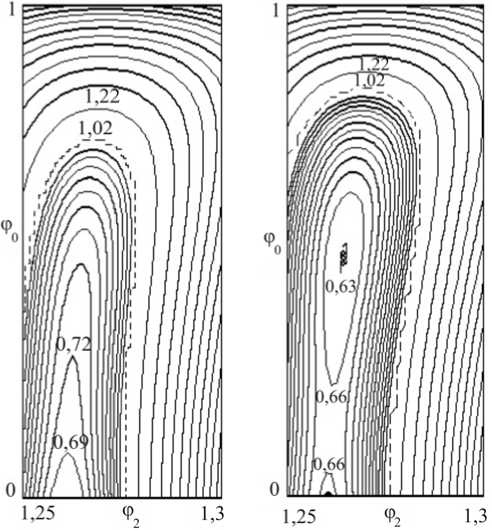
а
б
Рис. 3. Линии равного уровня значений целевой функции, полученные при фиксированных значениях радиуса притупления
в
При неудовлетворительном начальном приближении итерационный процесс метода Ньютона (3) может сходиться к другому решению (строка 2 табл. 1) или расходиться. В лучшем случае решение системы (2) может быть получено за 5-7 итераций при числе расчетов целевой функции порядка 100.
Рассмотрим в связи с этим применение метода циклического покоординатного спуска с переменным шагом варьирования параметров 8. Искомыми параметрами будем считать радиус притупления и углы ф 0 и ф 2 характеристического треугольника полинома Безье. Начальное значение шага 5 = 0,05, начальное значение r 0=0; ф 0= 1; ф 2 = 1,35, что не является хорошим начальным приближением метода Ньютона.
Последовательные приближения осуществляем, начиная с параметра ф 2, значение которого уменьшается от начального 1,35 до 1,25 (рис. 4, а , кривая 1 ), точки соответствуют вычисленным значениям целевой функции 5 D , отложенным по оси ординат. Варьирование параметра ф 0 (рис. 4, б ) приводит к установлению ф 0 = 0 (см. также рис. 3, а ), радиус притупления r0 = 0,05 (рис. 4, в ).
Результаты второго цикла вычислений с 5 = 0,05 шагом и полученными параметрами показаны на рис. 4, а - в кривыми 2 . Отмечается уменьшение относительного значения сопротивления 5 D ~ 1 %, но значения параметров далеки от оптимальных значений (приблизительно соответствуют приведенным в строке 2 табл. 1).
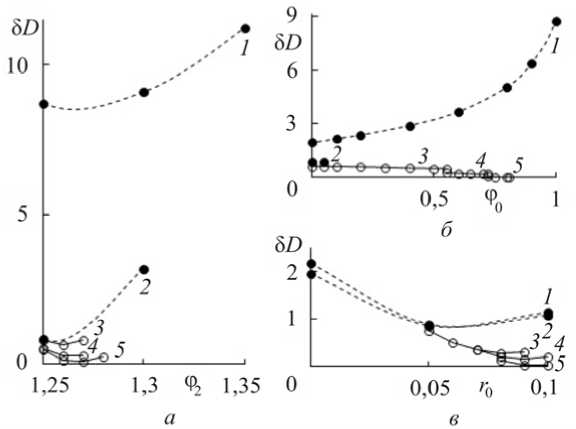
Рис. 4. Изменение целевой функции в зависимости от параметров образующей на различных этапах покоординатного спуска (расчет в рамках МЛВ)
Дальнейшие изменения в решении происходят при уменьшении шага варьирования 5< 0,01. В этом случае в одном из расчетов значение r 0 становится большим 0,52 (см. рис. 3, б ), и параметр ф 0 достаточно быстро принимает значение, близкое ф 0 (см. кривая 3 на рис. 4, б ), как и остальные параметры в 3-5 циклах (рис. 4, кривые 3 - 5 , светлые точки). В целом можно отметить, что общее число расчетов в методе спуска с точностью 5 = 0,01 даже при неудовлетворительном начальном приближении оказалось не превышающим таковое в методе Ньютона.
Таким образом, для расчетов оптимальных форм на базе уравнений механики сплошных сред в осесимметричной постановке можно рекомендовать аппроксимацию образующей полиномом Безье с тремя параметрами и метод оптимизации на основе циклического покоординатного спуска.
3. Результаты расчетов в осесимметричной постановке
Система уравнений модели нелинейной сжимаемой жидкости в эйлеровых переменных в цилиндрической системе координат записывается следующим образом:
-
d ρ ρ u du du
— + р( Urr + Uzz ) =--r- , р r + p, r = 0, p z + Pz = 0, dt r dt dt
ρ0A θ ρ0
p = 2, θ= 1 - ,
(1 - λθ)2 ρ где ρ0 и ρ – начальная и текущая плотность; d/dt – полная производная по времени; символ после запятой означает дифференцирование по соответствующей переменной, константы А и λ определяются ударной адиабатой (6).
Для определения сопротивления тела решается задача обтекания методом установления. В начальный момент времени давление в грунте равно нулю, скорость частиц грунта равна скорости удара и направлена вдоль оси вращения тела. Внешние границы расчетной области грунта отнесены достаточно далеко, чтобы возмущения, отражающиеся от них, не исказили численное решение в области контакта тела и среды. Неподвижный ударник считается жестким. На головной части ударника, контактирующей с грунтовой средой, принимается условие «непроницаемости» по нормали со «скольжением по касательной». Определенная таким образом сила сопротивления соответствует силе на квази-стационарной стадии внедрения с постоянной скоростью, полученной в прямом ударе.
Численные расчеты проводятся в рамках методики, основанной на модифицированной схеме Годунова первого порядка точности, реализованной в пакете прикладных программ «Динамика-2» [36]. Применимость известной численной методики и пакета программ к расчету параметров процессов проникания жестких и деформируемых ударников в мягкие грунтовые среды показана ранее [37]. Численные расчеты проводятся при тех же значениях параметров среды, что и в п. 2.
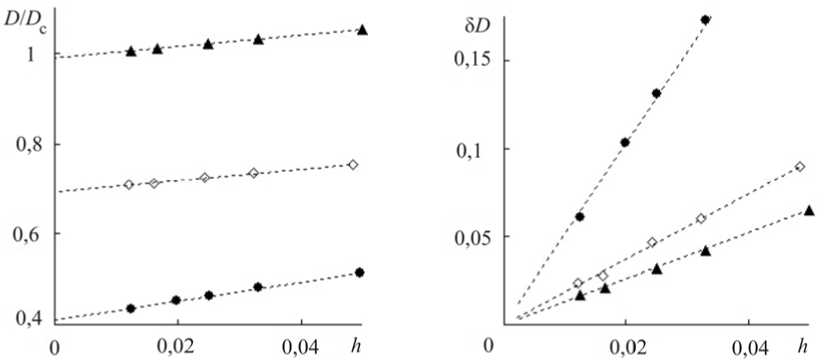
Анализ точности используемой численной методики показал практически линейную монотонную сходимость решений (рис. 5) в зависимости от шага сетки h = H / n , где H – длина образующей тела; n – число узлов разностной сетки. На рис. 5, а треугольниками, ромбами и точками обозначены соответственно рассчитанные численно значения сопротивления конуса D 1 и оптимальных тел, полученных в рамках МЛВ ( D 2 ) и в осесимет-ричных численных расчетах ( D 3 , см. далее).
б
а
Рис. 5. Анализ сходимости результатов численных расчетов проникания тел вращения при изменении шага сетки: а – безразмерные силы сопротивления внедрению; б – относительные погрешности определения сопротивления
Значение сопротивления каждого тела D i , i =1, 2, 3 отнесено к сопротивлению конуса D c , определенного в рамках МЛВ: Dc = f ( а ) = C /6. Пунктирные линии соответствуют линейным аппроксимациям методом наименьших квадратов.
Обозначим прогнозируемые при h = 0 значения сопротивления для каждого тела D * , i =1, 2, 3. На рис. 5, б (обозначения, как на рис. 5, а ) приведены относительные погрешности определения сопротивлений 5 D i = D * - 1, i = 1, 2, 3. При одинаковом размере ячейки разностной сетки h (выбирались близкие к квадратным ячейки сетки) отмечается большая погрешность для затупленного тела.
Далее приводятся результаты определения параметров образующей оптимального тела при проникании в грунт на основе численных осесимметричных расчетов. Начальное приближение применяемого метода циклического покоординатного спуска приведено в строке 1 табл. 1, 5 =0,05, порядок варьирования параметров ф 2- ф 0- г0 - ф 2, как в п. 2.
На рис. 6 приведены значения целевой функции 5D в зависимости от изменяемых в процессе покоординатного спуска параметров. Видно, что процесс последовательных приближений качественно близок к приведенному ранее на рис. 4. В первом цикле вычислений значение параметра ф0 уменьшается до 0 (рис. 6, б), видно, что сопротивление незначительно меняется при 0,2 < r0 < 0,3 (рис. 6, в).
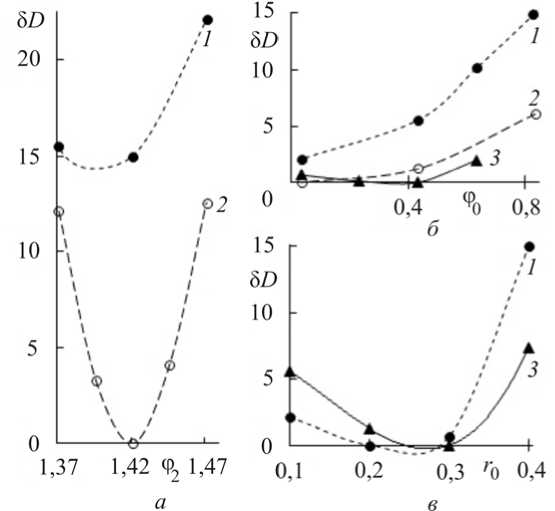
Рис. 6. Изменение целевой функции в зависимости от параметров образующей на различных этапах покоординатного спуска (расчеты в осесимметричной постановке)
Далее полагаем r0 = 0,2. Результаты второго цикла вычислений с полученными параметрами показаны на рис. 6, а , б кривыми 2 , отмечается уменьшение относительного значения сопротивления 5 D .
Кривые 3 на рис. 6 соответствуют расчетам при r 0 = 0,3. Величина ϕ 2 осталась практически без изменений, значение сопротивления тела равно минимальному при φ 0 = 0,434. Результаты расчетов сведены в табл. 2.
Таблица 2
Параметры оптимального тела в осесимметричной постановке
|
N |
P 0 ( r , z ) |
P 1 ( r , z ) |
P 2 ( r , z ) |
φ 0 |
φ 2 |
D |
|
3 |
(0,096; 0) |
(0,419; 0,356) |
(1; 2,236) |
0,834 |
1,271 |
0,1299 |
|
3 |
( 0,296 ; 0) |
( 0,688; 0,179 ) |
(1; 2,236) |
0,434 |
1,42 |
0,0797 |
|
3 |
( 0,196; 0) |
( 0,66 ; 0 ) |
(1; 2,236) |
0 |
1,42 |
0,0797 |
В первой строке табл. 2 приведены параметры оптимального тела, полученного в п. 2 в рамках МЛВ, отличие составляет значение сопротивления D , которое несколько уменьшилось. Вторая и третья строки представляют искомые параметры образующей оптимальных тел, обладающих одинаковым сопротивлением (в рамках погрешности численных расчетов порядка 1 %). Образующие тел с этими параметрами приведены на рис. 2 сплошной и пунктирной кривыми 2 соответственно. Отметим качественно похожее поведение численных решений в постановках на основе МЛВ и механики сплошных сред, но существенное отличие в формах оптимальных тел (см. рис. 2) и их сопротивлении (см. рис. 5, а ). Как отмечалось выше, полученное различие в силах сопротивления оптимальных тел для модели грунта – нелинейной жидкости является наибольшим. Различие уменьшается при учете внутреннего и поверхностного трения, а также других особенностей динамического деформирования грунтовых сред, численная реализация которых не представляет труда в рамках известных моделей грунтовых сред [1].
Заключение
Представлены результаты численного расчета методом локальных вариаций оптимальных форм осесимметричных ударников при движении в грунтовой среде. Установлено, что методика расчета полей давлений в окрестности головной части тела должна учитывать двумерные эффекты обтекания, однако предварительные исследования целесообразно проводить на базе известных упрощенных моделей, например локального взаимодействия. Показано, что метод циклического покоординатного спуска позволяет с точностью, определяемой погрешностью численных расчетов, вычислять параметры образующей тела вращения, которая может быть представлена полиномом Безье второй степени.
Разделы 1, 2 статьи выполнены при частичном финансировании в рамках базовой части государственного задания Минобрнауки РФ (проект № 2014/134 2226), раздел 3 при поддержке РНФ (грант №15-19-10039).
Список литературы Методика численного расчета оптимальных форм тел вращения при движении в грунтовой среде
- Сагомонян А.Я. Проникание. -М.: Изд-во МГУ, 1974. -299 с.
- Аптуков В.Н., Муpзакаев P.Т., Фонаpев А.В. Пpикладная теоpия пpоникания. -М.: Наука, 1992. -105 с.
- Высокоскоростное взаимодействие тел/под ред. В.М. Фомина. -Новосибирск: Изд-во СО РАН, 1999. -600 с.
- Аптуков В.Н., Петрухин Г.И., Поздеев А.А. Оптимальное торможение твердого тела неоднородной пластиной при ударе по нормали//Изв. АН СССР. Механика твердого тела. -1985. -№ 1. -С. 165-170.
- Аптуков В.Н., Хасанов А.Р. Оптимизация параметров слоистых плит при динамическом проникании жесткого индентора с учетом трения и ослабляющего эффекта свободных поверхностей//Вестник Пермского национального исследовательского политехнического университета. Механика. -2014. -№ 2. -С. 48-75
- Ben-Dor G., Dubinsky A., Elperin T. Shape optimization of high-speed penetrators: a review//Central European Journal Engineering. -2012. -Vol. 2. -No 4. -Р. 473-482. DOI: DOI: 10.2478/s13531-012-0022-4
- Ben-Dor, G., Dubinsky, A., Elperin, T. Engineering models of high speed penetration into geological shields//Central European Journal of Engineering. -2014. -Vol. 4. -No. 1. -Р. 1-19. DOI: DOI: 10.2478/s13531-013-0135-4
- Некоторые аналитические и численные оценки параметров оптимальной структуры защитной плиты/Н.В. Баничук //Проблемы прочности и пластичности: межвуз. сб. -Н. Новгород: Изд-во Нижегород. гос. ун-та, 2013. -Вып. 75. -№ 3. -С. 206-214.
- Остапенко Н.А., Якунина Г.Е. О телах наименьшего сопротивления, двигающихся в средах при наличии закона локальности//Изв. РАН. Механика жидкости и газа. -1992. -№ 1. -С. 95-106.
- Симонов И.В., Осипенко К.Ю. Устойчивость, траектории и динамический изгиб затупленного тела вращения при проникании в упругопластическую среду//Прикладная механика и техническая физика. -2004. -№ 3. -C. 146-160.
- Баженов В.Г., Котов В.Л. Решение задач о наклонном проникании осесимметричных ударников в мягкие грунтовые среды на основе моделей локального взаимодействия//Прикладная математика и механика. -2010. -Вып. 74, № 3. -С. 391-402.
- Расчет проникания недеформируемых ударников в малопрочные преграды с использованием данных пьезоакселерометрии/В.А. Велданов //Журнал технической физики. -2011. -Вып. 81, № 7. -С. 94-104.
- Осипенко К.Ю. Об устойчивости пространственного движения тела вращения в упругопластической среде//Известия РАН. Механика твердого тела. -2012. -№ 2. -С. 68-77.
- Анализ моделей расчета движения тел вращения минимального сопротивления в грунтовых средах/В.Г. Баженов //Прикладная математика и механика. -2014. -Вып. 78, № 1. -С. 98-115.
- Якунина Г.Е. К построению оптимальных пространственных форм в рамках модели локального взаимодействия//Прикладная математика и механика. -2000. -Вып. 64, № 2. -С. 299-309.
- Остапенко Н.А. Тела вращения минимального сопротивления при движении в плотных средах//Успехи механики. -2002. -№ 2. -С. 105-149.
- Якунина Г.Е. Об особенностях движения оптимальных тел в плотных средах//Доклады Академии наук. -2011. -Вып. 439, № 1. -С. 51-55.
- Якунина Г.Е. Особенности высокоскоростного движения тел в плотных средах//Прикладная математика и механика. -2012. -Вып. 76, № 3. -С. 429-449.
- Баничук Н.В., Иванова С.Ю. Оптимизация формы жесткого тела, внедряющегося в сплошную среду//Проблемы прочности и пластичности: межвуз. сб. -Н. Новгород: Изд-во Нижегород. гос. ун-та, 2007. -Вып. 69. -С. 47-57.
- Ben-Dor G., Dubinsky A., Elperin T. Shape optimization of impactors against a finite width shield using a modified method of local variations//Mechanics Based Design of Structures and machines. -2007. -Vol. 35. -Р. 113-125. DOI: DOI: 10.1080/15397730701196629
- Ben-Dor G., Dubinsky A., Elperin T. Modification of the method of local variations for shape optimization of penetrating impactors using the localized impactor/shield interaction models//Mechanics Based Design of Structures and machines. -2007. -Vol. 35. -Р. 1-14. DOI: DOI: 10.1080/15397730601120570
- Применение модели локального взаимодействия для определения силы сопротивления внедрению ударников в песчаный грунт/В.Л. Котов //Прикладная механика и техническая физика. -2013. -Вып. 54, № 4. -C. 114-125.
- Баженов В.Г., Котов В.Л., Линник Е.Ю. О моделях расчета форм осесимметричных тел минимального сопротивления при движении в грунтовых средах//Доклады Академии наук. -2013. -Вып. 449, № 2. -С. 156-159. DOI: DOI: 10.7868/S0869565213080082
- Таковицкий С.А. О сходимости в задаче оптимизации крыла сложной формы//Журн. вычисл. матем. и матем. физ. -2002. -Вып. 42, № 5. -С. 690-697.
- Таковицкий С.А. Аналитическое решение в задаче построения осесимметричных носовых частей минимального волнового сопротивления//Изв. РАН. Механика жидкости и газа. -2006. -№ 2. -С. 157-162.
- Крайко А.А., Пьянков К.С. Эффективные прямые методы в задачах построения оптимальных аэродинамических форм//Журн. вычисл. матем. и матем. физ. -2010. -Вып. 50, № 9. -С. 1624-1631.
- Котов В.Л., Линник Е.Ю. Численный расчет формы тела вращения минимального сопротивления движению в грунтовой среде в рамках модели локального взаимодействия//Проблемы прочности и пластичности: межвуз. сб. -Н. Новгород: Изд-во Нижегород. гос. ун-та, 2013. -Вып. 75, № 4. -С. 296-302.
- Котов В.Л., Линник Е.Ю. Численный расчет оптимальной формы тела вращения при движении с постоянной скоростью в грунтовой среде//Вычислительная механика сплошных сред. -2014. -Вып. 7, № 2. -С. 142-150. DOI: DOI: org/10.7242/1999-6691/2014.7.2.15
- Черноусько Ф.Л., Баничук Н.В. Вариационные задачи механики и управления: Численные методы. -М.: Наука, 1973. -238 с.
- Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. -М.: Наука, 1976. -278 с.
- Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и на производстве: пер. с англ. -М.: Мир, 1982. -304 с.
- Аптуков В.Н. Расширение сферической полости в упругопластической среде при конечных деформациях. Сообщение 1. Влияние механических характеристик, свободной поверхности, слойности//Проблемы прочности. -1991. -№ 12. -С. 7-11.
- Forrestal M.J. Tzou D.Y. A spherical cavity-expansion penetration model for concrete targets//International Journal of Solids and Structures. -1997. -Vol. 34 (31-32). -Р. 4127-4146. DOI: DOI: org/10.1016/S0020-7683(97)00017-6
- Omidvar M., Iskander M., Bless S. Response of granular media to rapid penetration//International Journal of Impact Engineering. -2014. -Vol. 66. -Р. 60-82. DOI: DOI: org/10.1016/j.ijimpeng.2013.12.004
- A model of depth calculation for projectile penetration into dry sand and comparison with experiments/Cuncheng Shi, Mingyang Wang, Jie Li, Mengshen Li//International Journal of Impact Engineering. -2014. -Vol. 73. -Р. 112-122. DOI.org/10.1016/j.ijimpeng.2014.06.010
- Пакет программ «Динамика-2» для решения плоских и осесимметричных нелинейных задач нестационарного взаимодействия конструкций со сжимаемыми средами/В.Г. Баженов //Мат. моделирование. -2000. -Вып. 12, № 6. -С. 67-72.
- Баженов В.Г., Брагов А.М., Котов В.Л. Экспериментально-теоретические исследования процессов проникания жестких ударников и идентификация свойств грунтовых сред//Прикладная механика и техническая физика. -2009. -Вып. 50, № 6. -С. 115-125.


