Методика дискретного управления электродвигателем постоянного тока
Автор: Айдинян Андрей Размикович, Цветкова Ольга Леонидовна, Молчанов Александр Алексеевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 3 (78) т.14, 2014 года.
Бесплатный доступ
Рассмотрена методика дискретного управления непрерывным объектом на примере двигателя постоянного тока. Предлагаемая методика позволяет упростить процесс выбора желаемых свойств синтезируемой системы управления, свести нахождение управления к стандартной задаче решения системы линейных уравнений с учётом ограничений-неравенств на каждом шаге дискретизации по времени. Желаемые свойства синтезируемой системы задаются с помощью эталонного переходного процесса. Используется квадратичный критерий качества, характеризующий отклонение переходного процесса от эталонного в равноотстоящие моменты времени. Такой подход позволяет в реальном масштабе времени управлять объектом с учётом ограничений как на управляющее воздействие, так и на фазовые координаты системы управления. При этом можно добиться отсутствия перерегулирования и колебательности.
Управляющее воздействие, система управления, вектор состояния, двигатель постоянного тока
Короткий адрес: https://sciup.org/14250094
IDR: 14250094 | УДК: 681.511.4 | DOI: 10.12737/5713
Текст научной статьи Методика дискретного управления электродвигателем постоянного тока
Введение. Электродвигатели постоянного тока являются непрерывными объектами. В то же время для реализации управления всё большее применение находят средства, использующие представление информации в дискретной форме. Причём управление должно строиться с учётом нелинейных свойств объектов управления и реальных ограничений на фазовые координаты и управляющее воздействие.
Для решения задач оптимального управления большое распространение получили методы, опирающиеся на использовании минимизируемых функционалов. Существующие методы синтеза можно разделить на две группы: методы, использующие косвенные критерии качества, и методы, использующие прямые критерии качества.
К методам синтеза оптимальных систем управления с использованием косвенных критериев качества относятся принцип максимума Понтрягина [1] и принцип оптимальности Беллмана [2]. Эти принципы являются мощными математически обоснованными способами решения оптимизационных задач в отношении минимизации выбранного критерия качества. Синтез систем управления с помощью принципа максимума Понтрягина сводится к решению двухточечной краевой задачи для дифференциальных уравнений [1]. Получение аналитического выражения для оптимального управления в замкнутой форме связано с большими трудностями и представляет собой самостоятельную задачу для каждого класса объектов [3]. Трудности решения двухточечных краевых задач стимулировали поиск разного рода прямых методов [4-6].
В данной статье предлагается методика сведения задачи нахождения управляющего воздействия для нелинейной системы управления к решению системы линейных алгебраических уравнений на каждом шаге квантования по времени. При этом требуется обеспечить отсутствие перерегулирования, колебательности и учесть ограничения на фазовые координаты и управляющее воздействие.
Для задания желаемых свойств переходного процесса предлагается использовать квадратичный критерий качества, характеризующий отклонение переходного процесса от эталонного в равноотстоящие моменты времени.
Математическая модель объекта управления. При упрощённом исследовании электродвигателей постоянного тока с использованием линеаризованных математических моделей обычно принимают следующие допущения: гистерезис в магнитной цепи отсутствует, то есть намагничи-
Работа выполнена по теме № 01201259781 в рамках выполнения Госзадания Минобрнауки России в части НИР.
вающая сила однозначно определяет магнитный поток; размагничивающее действие реакции скомпенсировано; сопротивление и индуктивность якоря не зависят от значения тока возбуждения, тока якорной цепи и других факторов и считаются неизменными; к валу двигателя со стороны машины приложен электромагнитный момент М, а все моменты, обусловленные механическими потерями, входят в момент сопротивления нагрузки Мс = Mc(t, а, со); момент инерции привода не зависит от параметров его движения; управление осуществляется по одному каналу.
Таким образом, электродвигатель постоянного тока с независимым возбуждением описывается системой дифференциальных уравнений следующего вида:
da
—— = CD, dt
dm km kmk 1
dt JR JR J где R — сопротивление якорной цепи; а — угол поворота вала двигателя; со — угловая скорость вала двигателя; Мс(со) — момент сопротивления на валу двигателя; J — момент инерции, приведённый к валу двигателя; km, km — параметры, характеризующие электромеханические свойства электродвигателя; и — напряжение в цепи якоря.
Без потери общности момент нагрузки на валу двигателя будем считать равным
MC(J) = С • to , где с — некоторый коэффициент. В случае нелинейного момента на линеаризацию на каждом шаге квантования.
Система уравнений, описывающая электродвигатель является представлена в матрично-векторном виде [7]:
x(t) = Ax(t) + Bu(t),
валу можно осуществить
линейной и может быть
О
где х^ =
со
— вектор-столбец состояния электродвигателя; А =
матрица параметров системы; В =
О
А
JR,
О
JR
R
— постоянная
— постоянный вектор-столбец параметров системы;
u(t) — управляющее воздействие.
Методика управления. Дискретные модели объектов строятся в предположении, что управляющие воздействия, формируемые в ЭВМ в виде цифровых кодов, преобразуются в непрерывные процессы с помощью экстраполяторов нулевого порядка. На практике в качестве экстраполя-торов нулевого порядка используются цифроаналоговые преобразователи [6].
Рассмотрим задачу перевода системы из начального состояния в нулевое. На управление и вектор состояния наложены ограничения [8]:
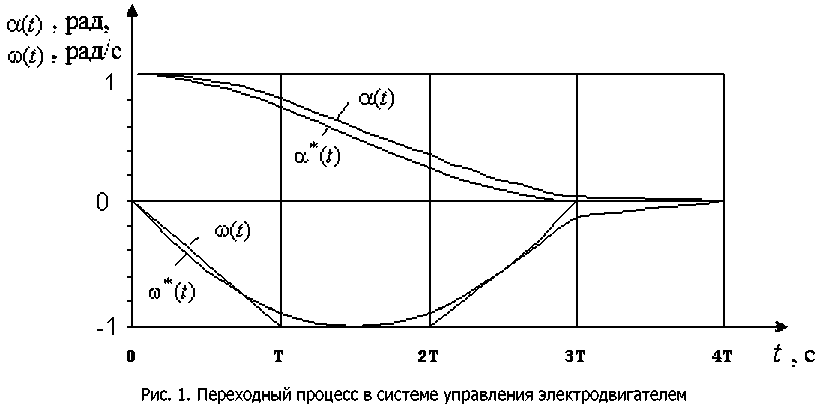
Ain О(П < Umax , xmm (3) (4) На каждом k-м интервале дискретизации по времени объект управления (2) будет описываться уравнением [9]: хк ^ = Ахк ^ + Вик, а решение этого уравнения в моменты дискретизации описывается линейными разностными матричными уравнениями вида: xM=eMxtW)uk kT+T где Р(Т) = J" eA<-kT+T~^Bdi; Т — период дискретизации кТ Для решения задачи перевода вала из начального состояния х0 = {а(0) = ао;ю(О) = ю0} в конечное х„пн =ta(tH )= а ■ ® 1 с минимальными потерями энергии в якоре, эталонный переходный процесс будем выбирать на основе известной процедуры построения оптимальной диаграммы тока и скорости, так чтобы переходный процесс заканчивался за 4 шага дискретизации по времени (период дискретизации Тпримем равным 0,013 с). Определим последовательность uk таким образом, чтобы минимизировать сумму квадра тов отклонений от эталонного переходного процесса в моменты квантования. Тогда критерий ка чества представляется в виде: IX Л min, k=0 где 6k = xk -xk — вектор ошибки размерности 2 в моменты дискретизации; хк — вектор состояния эталонного переходного процесса размерности 2 в моменты времени кТ. Тогда задача синтеза как задача о наименьших квадратах с линейными ограничениями-неравенствами формулируется следующим образом [10]: минимизировать Г<М1 (5) при условии GU>h, (6) где Е, f, G, h, U— соответственно /?х m-матрица, /т-вектор, I х m -матрица, /-вектор, лт-вектор. Для сформулированной задачи необходимо минимизировать: I * 1^ I * I X Х+1 “ Хк+1 ' к+1 “ **+1 к-0 с учётом ограничений (3) и (4). Поскольку переходный процесс заканчивается за 4 шага, выражение (7) примет вид: -> min. Метод наименьших квадратов для решения задачи менное нахождение всех неизвестных с помощью решения оптимизации предполагает одновре-одной системы линейных уравнений [10]. Поэтому при нахождении u^i = 0,3) необходимо в вектор неизвестных (/включить все UjU = G,$. Введём вектор неизвестных U = lu0,uvu2,u3Y. Определение такого вектора неизвестных позволяет построить программное управление. С целью построения замкнутой системы управления после нахождения вектора неизвестных на первом шаге дискретизации на вход подаётся управляющее воздействие, сформированное с помощью системы базисных функций и вектора и0. Векторы ulzu2,u3 не участвуют в формировании управляющего воздействия. Однако вектор и3 используется для определения действия ограничений на управляющее воздействие на шаге дискретизации 4. Нахождение управляющего воздействия для второго шага дискретизации по времени происходит путём решения системы уравнений с ограничениями после измерения состояния на "i первом шаге. В этом случае вектор неизвестных равен U = Для формирования управления на втором шаге используется вектор и1. Следовательно, включение в вектор неизвестных управлений на всём периоде действия ограничений позволяет синтезировать оптимальную систему управления путём решения последовательности линейных алгебраических уравнений. Предлагаемый способ учёта ограничений позволяет гарантировать их жёсткое соблюдение в отличие от использования штрафных функций. Формирование матриц для решения задачи управления. Сформируем матрицу Е и вектор f, входящие в матричное выражение (5). Для этого найдём выражение для вектора состояния системы и эталонного вектора состояния в моменты времени КТ + Т, где к = 0,3. Для каждого /с-го шага (к = 1,4) вычислим значения эталонного переходного процесса по формуле у _ ^кп у лк ~с л0 Переходный процесс в системе определяется выражениями 'хм = еАТх( +P(T)ui, х,_2 = еАТ xul + py^u^ = егАТX; + еАТРУ') • и, + P(DuKV xj+3 = eATxi+2 + Р(Г)у/+2 = e^Xj + е2АТР(Г)и/ + еАТР(Г) • ui+1 + P(T)uit2, xM = eATxi+3 + P(T^u,+3 = еААТх, + еЗАТР(Г)и, + e2ATP^Uj^ + e^P^ • u/+2 + Р(Г)у,+3 Согласно методу обратной задачи динамики [4, 11] подставим выражение (8) для х*к+1 (к = 0, 3) в левую часть системы уравнений (9) вместо хк+1, получим Р^Т) 0 00 еАТ .Р(Т) Р(Т) 00 е2^ . р(т) еАТ ■ Р(Г) Р(Т)0 еЗАТ Р^ е2АТ Р(Т) еАТ Р(Г) Р(Г) Матрица Е имеет размерность 8x4, а вектор f — размерность 8. Сформируем матрицу G и вектор h. Запишем ограничения (3) и (4) на управление и век тор состояния в виде “к > Vmin, -ик > "Umax, у > У лк+1 - ^min' _у > _ У . Ак*\- А max для всех к = 0,3. Подставив выражения (9) для хк+1 в систему неравенств (10), получим 'о о ч (И) -eATx0-P(JX^-Xmax, e2ATx0+eATP(JX+P Представляя неравенства (11) в матричном виде, получаем выражения для матрицы G размерности 16 х 4 и вектора h размерности 16: G = " 1 0 0 0" -10 0 0 "^max 0 10 0 0-100 "^max 0 0 10 0 0-10 -Umax 0 0 0 1 uZ 0 0 0 -1 "^max р(П о оо h = Y _ aAT у Amin c л0 -Р(Г) 0 0 0 — Y -I- y лтах c л0 еАТРУ^ Р(Т) 0 0 Amin c л0 -еАТР(Л -Р(Т) 0 0 _ Y _i_ p2-AT у Amax c л0 e2ATP(T) eATPU^ Pd) 0 Y v Лт1п “ “ Л/ -e2"?^ -eATP{T) -P(T) 0 _ y -I- y лтах л0 e2ATP(J^ e2ATP{T) eAT P(T) P(J) %min - e4/,rxz -e^P^T) -e2ATP(J) -еАТР(Л -Р<Л _ Y _i_ p^AT у _ Amax^c л0_ Результаты моделирования. Синтезируем систему управления электродвигателем постоянного тока ДПМ-25. На рис. 1 приведены графики переходного процесса в системе управления, эталон- ного переходного процесса и их производных, полученные при равенстве матриц ^1 = ^2 = ^3 = И «а = 1000 0 . Выбор матрицы R на 4-м шаге со значительно большим первым диагональным элементом объясняется желанием обеспечить на последнем шаге мини мально возможное отклонение положения от эталонного Переходный процесс получен путём численного решения системы дифференциальных уравнений — (1), описывающих исследуемую систему с учётом электрической цепи якоря, с шагом равным Т/8. При синтезе учитывались ограничения на величину управляющего воздействия (напряжение на якоре) вида -1 < t/(f) <1 и величину скорости вала двигателя вида -1 < m(f) <1. Для того чтобы гарантировать отсутствие перерегулирования вала двигателя, наложены ограничения «(f) > 0. Заключение. На примере синтеза управления электродвигателем постоянного тока показано, что благодаря заданию желаемых свойств в виде эталонного переходного процесса и квадратичному критерию качества, характеризующего отклонение переходного процесса от эталонного, нахождение управления сводится к решению системы линейных уравнений с линейными ограничениями-неравенствами в реальном масштабе времени.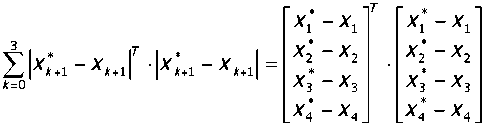
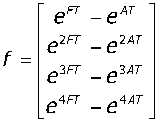
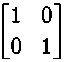

Список литературы Методика дискретного управления электродвигателем постоянного тока
- Математическая теория оптимальных процессов/Л. С. Понтрягин [и др.]. -Москва: Наука, 1983. -393 с.
- Беллман, Р. Динамическое программирование/Р. Беллман. -Москва: Иностр. лит., 1960. -400 с.
- Летов, А. М. Аналитическое конструирование регуляторов/А. М. Летов//Автоматика и телемеханика. -1960. -Т. 21, № 4. -С. 436-442.
- Крутько, П. Д. Обратные задачи динамики управляемых систем: Линейные модели/П. Д. Крутько. -Москва: Наука, 1987. -304 с.
- Нейдорф, Р. А. Композиционный синтез квантиоптимальных по быстродействию систем управления высокого порядка/Р. А. Нейдорф, Н. Н. Чан//Вестн. Дон. гос. техн. ун-та. -2007. -Т. 7, № 4 (35). -С. 353-359.
- Amin, M. H. Optimal discrete systems with prescribed eigenvalues//Int. J. Control, 1984, vol. 40, no. 4, pp. 783-794.
- Timothy, L., Bona, B. State Space Analysis. N. Y., McGraw-Hill, 1968, 406 p.
- Юрченко, Д. В. Сравнение ограниченного и неограниченного управлений с обратной связью для стохастической линейно-квадратичной задачи/Д. В. Юрченко//Автоматика и телемеханика. -Москва, 2006. -№ 7. -С. 88-94.
- Стрейц, В. Метод пространства состояний в теории дискретных линейных систем управления. -Москва: Наука. Гл. ред. физ.-мат. лит., 1985. -296 с.
- Lawson, Ch., Henson, R. Solving Least Squares Problems. New Jersey, Prentice-Hall, 1974,
- p.
- Брагина, А. А. Обратная задача в управлении динамической системой/А. А. Брагина//Вестник Южно-Ур. гос. ун-та. Серия: Мат. моделирование и программирование. -Челябинск, 2012. -№ 40. -С. 162-166.


