Методика двухстадийного расчёта армирования элементов железобетонных каркасных зданий и сооружений на действие сейсмических сил с применением концепции нелинейного статического анализа. Часть 1: постановка задачи, структура методики, информационная база исследования и стратегия определения параметров зон пластичности

Введение. Постановка задачи

Главная задача проектирования зданий и сооружений в сейсмических районах – предотвращение обрушения системы в целом при сильном (редком) землетрясении. Как показали, например, Спитакское (1988) и Шикотанское (1994) события, применение только линейноспектрального метода (далее – ЛСМ) не всегда гарантирует обеспечение требуемого уровня сейсмостойкости железобетонных каркасных зданий и сооружений массового1 строительства. Коэффициент допускаемых повреждений K1 учитывает пластическую реакцию объектов исследования только при слабо нелинейном характере работы конструкций. Незначительная (до 20 %) поправка к значениям коэффициента K1, внесённая в табл. 4 актуализированных редакций СНиП II-7–81*, не способна оказать существенного влияния на повышение сейсмостойкости объектов исследования [1], поскольку она, как правило, перекрывается конструктивными (нерасчётными) мероприятиями правил проектирования. Реализованным в них требованиям, касающимся учёта особенностей неупругого деформирования конструкций при сильных (редких) землетрясениях, присущ поверхностно-декларативный характер. Логические связи между конструктивными мероприятиями и расчётными параметрами зон пластичности несущих элементов, ответственных в остове системы за рассеяние энергии землетрясения, в нормах отсутствуют. При этом понятие «зоны пластичности» не подкреплено каким-либо математическим аппаратом. В практике проектирования железобетонных конструкций объектов массового строительства внимание инженера в основном сфокусировано на расчёте продольной арматуры по прочностному критерию. Нельзя назвать достаточными для целей сейсмостойкого проектирования требования норм к диаграмме состояния бетона, обжатого контуром поперечного армирования в объёме расчётного участка зон пластичности. К тому же, для расчётов на упруго-пластических моделях не определены критерии необрушения при действии сейсмических сил. Все перечисленные недочёты выявляются сопоставлением требований отечественных норм с результатами обследования последствий разрушительных землетрясений, положениями передовых зарубежных исследований и регламентов в области проектирования сейсмостойких конструкций [1–5]. Поэтому расчёты по пункту 5.2(б) СП 14.13330.2014 (далее – свод правил) оказываются не под силу рядовому инженеру. Выполняя их с учётом пункта 5.2.2 свода правил, даже продвинутые специалисты могут получить разные результаты, поскольку многое зависит от параметров учитываемого сейсмического воздействия.

В качестве альтернативы инженер может рассмотреть методики добровольного применения, разработанные на базе различных профилирующих (ведомственных) организаций. Однако они, как правило, не определяют порядок и способ учёта влияния конструктивных мероприятий и расчётных параметров зон пластичности в несущих конструкциях на реализацию механизма деформи- рования системы при расчётном событии. В настоящем исследовании автором предпринята попытка раскрыть обозначенные нюансы, дополнительно пояснить сущность понятия «оценки сейсмостойкости по критерию необрушения» и пополнить базу знаний рядового расчётчика, занятого в проектировании и поверочной оценке категории технического состояния каркасных зданий и сооружений в сейсмических районах. На обозрение читателю предлагается прикладная методика (в двух частях), содержащая в своей основе положения концепции метода нелинейного статического анализа (далее – НСМ). Работа направлена на дальнейшее развитие расчётных положений, изложенных автором в публикациях [1, 6, 7].

1. Определения и обозначения, применяемые в методике

В методике автором применяются и дополнительно раскрываются следующие основные определения и обозначения:

зоны пластичности – области вероятного накопления локальных повреждений в элементах несущих конструкций, характеризующих способность системы к рассеиванию энергии воздействия и подлежащие специальному конструированию для обеспечения реализации допускаемого механизма пластического деформирования, но не приводящие к выходу из строя системы в целом;

эквивалентная длина зоны пластичности L_p – участок консолидации прогнозируемых пластических деформаций в элементе несущей конструкции (от англ. lumpedplasticity), на котором его прогиб допускается принимать с постоянным значением; в первом приближении назначается в несущих конструкциях на стадии концептуального проектирования системы;

критическое сечение зоны пластичности (по T. Paulay и I.N. Bull , 1979 [8]) – сечение элемента плоскостью, перпендикулярной к его продольной оси, расположенное в начале расчётного участка зоны пластичности (например, на конце псевдоконсоли или вута ригеля рамы каркаса);

приузловой участок – участок ригеля и/или колонны, примыкающий к жёсткому узлу рам объектов исследования, предназначенный для установки принимаемой по расчёту замкнутой поперечной арматуры (хомутов);

параметр затухания ξ 0 (кси с индексом «0») – дополнительное затухание колебаний в упругопластической стадии, реализующееся за счёт повреждения несущих конструкций, ответственных за образование допускаемого механизма пластического деформирования [9];

критерий необрушения – условие наступления повреждения несущих конструкций здания (сооружения) на стадии, предшествующей предельному состоянию системы, при котором она ещё способна обеспечить сейсмическую безопасность жизни людей и ценного оборудования в рассмат- риваемой постановке задачи (например, при новом проектировании, реконструкции, оценке дефицита сейсмостойкости или при сейсмоусилении конструкций критерии будут отличаться);

коэффициент масштабирования незаполненно-го/«чистого» каркаса K S (по И.Л. Корчинскому, 1971 [10, с. 186]) – отношение периода собственных колебаний здания, определённого преимущественно экспериментальным путём с учётом влияния второстепенных конструкций (стенового заполнения, самонесущих стен, перегородок, стальных лестниц, навесных стеновых панелей) и основания, к теоретическому значению периода, найденному расчётным путём без учёта жесткостных параметров второстепенных конструкций на недеформируемом основании;

предельный коэффициент деформативности K Z (кр) (по А.И. Мартемьянову, 1967 [11]) – отношение периода собственных колебаний здания, находящегося в состоянии перед достижением предельного состояния, к значению периода колебаний, соответствующему стадии введения его в эксплуатацию (представительный обзор значений K_Z ( _кр ) приведён в монографии А.С. Золоткова [12]);

параметр SF – коэффициент масштабирования (от англ. scale factor) расчётного спектра реакции (принят в соответствие с обозначениями, установленными в комплексах компании Computers & Structures, Inc);

точка упруго-пластических свойств системы – точка на кривой несущей способности системы, характеризующая уровень повреждения основных несущих конструкций, ответственных за реализацию механизма её пластического деформирования (англ. performance/target point; далее – точка свойств [13]);

угол поворота θ (в зоне пластичности приузло-вого участка) – угол между касательной (к упругой оси ригеля), проведённой через нейтральную ось критического сечения, и хордой, соединяющей эту точку с точкой перегиба ригеля в пролёте;

коэффициент C d – параметр, учитывающий отношение перемещений верха упругой системы и перемещений, полученных в результата по НСМ (англ. Displacement amplification factor); по своему функционалу C_d близок к требованию примечания 2 табл. 4 СП 14.13330.

Другие термины и определения, встречающиеся в тексте, приведены автором в статьях [1, 14].

• 2.    Обзор методик, учитывающих понятие кривой равновесных состояний при оценке сейсмической реакции каркасных систем и составляющих информационную базу исследования

  • 2.1.    О методологии нелинейного

статического (Pushover) анализа

Оценить предельное состояние всякой реальной системы при сильном (редком) землетрясении с достаточной для практических целей точностью позволяет кривая равновесных состояний [1]. В зарубежной практике проектирования сейсмостойких конструкций считается, что основу кон- цепции её применения заложили Rosenblueth E., Herrera I. (1964), Gulkan P. и Sozen M.A. (1974). А в виде прикладной техники расчёта она была впервые представлена в 1975 году американским научным коллективом под руководством Зигмунда Фримана (S.A. Freeman, J.P. Nicoletti и J.V. Tyrell [15]). Для целей оценки сейсмостойкости 80 зданий в районе верфи военно-морской базы Пьюджит Саунд они разработали алгоритм, получивший название метод спектра несущей способности (англ. Capacity Spectrum Method – CSM; 1975; назовём его методом Фримана). Позднее он был учреждён в регламенте по расчёту и усилению железобетонных зданий в сейсмических районах АТС-40 (Seismic Evaluation and Retrofit of Concrete Buildings; 1996). Основные расчётные предпосылки указанного метода и порядок трансформации кривой равновесных состояний формата Vsh.b.–Δ в спектр несущей способности пояснены автором в работе [13]. На рис. 1 в обобщенном виде с комментариями автора представлена схема поиска точки свойств, положение которой на кривой несущей способности характеризует уровень повреждений конструкции при действии сейсмических сил [1]. Приходится отмечать, что в ряде зарубежных публикаций встречается неточность в трактовке такого понятия, как «траектория поиска расположения точки упруго-пластических свойств». Эту ломаную кривую или вообще не указывают при графическом обосновании получения точки свойств, или почему-то наделяют определением «demand spec-trum», в то время как этот англоязычный термин относится к понятию «расчётного спектра реакции» (полученного при демпфировании ξeff [9]).

За два крайних десятилетия стандартная (однокомпонентная, одномодовая по Фриману) нелинейная процедура получила дальнейшее развитие в виде ряда активно развивающихся модификаций. Их преобладающее большинство направлено на совершенствование нескольких особенностей: алгоритма поиска точки свойств системы, учёта вклада высших мод, учёта крутильных деформаций системы и пошаговой корректировки распределения внешних сил по её высоте. Фонд рассматриваемых модификаций включает методики2 таких исследователей, как P. Fajfar и M. Fischinger (N2-method; 1989), Kilar V. и Fajfar P. (Simplified PushOver Analysis – SPOA; 1996), P. Fajfar и P. Gaspersic (N2-method; 1996), K.K. Sasaki, S.A. Freeman и Paret T.F (Multi-Mode Pushover Procedure – MPP; 1998), P.A. Fajfar (Extended N2-method; 1999), U. Morelli и др. (Displacement Coefficient Method – DCM; 2000), A.K. Chopra и R.K. Goel (Modal Pushover Analysis – MPA; 2002), A.S. Moghadam (Pushover Results Combination –

Рис. 1. Визуализация концепции поиска точки свойств системы (по Фриману)

PRC; 2002), M.N. Aydinoglu (Incremental Response Spectrum Analysis – IRSA; 2003), T.S. Jan, M.W. Liu, Y.C. Kao (Upper-Bound Pushover Analysis – UBPA; 2004), A.K. Chopra, R.K. Goel и C. Chintana-pakdee (Modified Modal Pushover Analysis – MMPA; 2004), J. Hooper, G.A. MacRae и S.A. Mahin (Displacement Modification Method – DMM; 2005), Iwan W.D. и Guyader A. (Equivalent Linearization Method – ELM; 2005), E. Kalkan и S.K. Kunnath (Adaptive Modal Combination Procedure – AMC; 2006), M. Jianmeng, Z. Changhai и X. Lili (Improved Modal Pushover Analysis – IMPA; 2008) и M. Poursha, F. Khoshnoudian, A.S. Moghadam (Consecutive Modal Pushover – CMP; 2009) и др.

Учитывая количество, базис, цели и задачи вышеперечисленных процедур, автор предлагает объединить их общим понятием методологии нелинейного статического (Pushover) анализа. Основные положения, раскрывающие их сущность и расчётные особенности алгоритмов, приведены автором в работе [7]. Следует отметить, что преобладающее большинство этих работ направлено на получение только поверочных расчётных оценок сейсмостойкости (при заранее заданных параметрах армирования несущих элементов) при действии сейсмических сил установленной интенсивности. При этом многие из них не учитывают в основных несущих элементах конструктивные особенности зон пластичности. Поэтому их на пряжённо-деформированное состояние (далее – НДС) для реализации благоприятного механизма пластического деформирования конструктивной системы при сильном (редком) землетрясении было выбрано автором в качестве предмета исследования в объёме изложенной методики.

В итоге, в процессе изучения представленной проблематики [7], у автора сложилось устойчивое мнение, что модель концепции НСМ имеет прикладные отечественные прототипы, которые обсуждались научным сообществом ещё до анонсирования результатов исследований Фримана. Для подтверждения достоверности такого умозаключения рассмотрим в хронологическом порядке основные положения наиболее характерных из них.

• 2.2.    Способ оценки сейсмостойкости

  конструкций А.С. Тяна (1965) [16]

Объекты исследования – двумерные одноярусные рамные конструкции из идеального упруго-пластического материала. В качестве частного примера рассмотрена однопролётная рама высотой 5,0 м и пролётом 6,0 м с гравитационной нагрузкой приложенной к ригелю. Максимальное ускорение в уровне основания – 0,2g. Период собственных колебаний системы по низшему тону T1 = 0,363 с. Исходный закон восстанавливающей силы представлен диаграммой «горизонтальное перемещение – сила» формата3 x-R, которая приводится к билинейной аппроксимации с горизонтальной полочкой. Предельным состоянием системы считается её состояние перед образованием k1+1 (где k – степень статической неопределимости системы) числа неподвижных пластических шарниров; определяется такое состояние величинами xпр и Rпр. В качестве предельных значений изгибающих моментов М в пластических шарнирах принимаются значения, по которым подобраны сечения элементов в линейной постановке по прочностному критерию.

В качестве основного показателя оценки сейсмостойкости принято максимальное горизонтальное остаточное смещение системы μ max , определяемое из выражения:

Ц max = | ^x max| - x T , (1)

где xТ – горизонтальное перемещение, соответствующее упругому состоянию системы; xmaх – максимальное горизонтальное перемещение системы. Основной критерий обеспечения сейсмо- стойкости представлен условием: k|S( xПР - xT ) , xТ

где x пр – горизонтальное перемещение, соответствующее предельному состоянию системы; k ₁ – степень развития пластических деформаций, определяемая из выражения:

k = ^ц max x_T

.

Дополнительно в работе [16] обозначены ещё два показателя оценки сейсмостойкости – k 2 и k 3 :

x пл max

: 2 = y max

где xпл max – максимальное перемещение упругопластической системы; x – максимальное пе-ymax ремещение упругой системы (по сути, k2 – это коэффициент пластичности μR – А.С. [1]). Энергетический критерий сейсмостойкости по Тяну представлен показателем k3:

, _ Ann max _ 0’5 Rap xT + Rp ^max _ k-i =         =                        = ymax        , xymax ymax

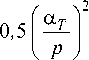
^{+ a} T ^max

0 , 5 p ² x ²

ymax

,

где Aпл max – работа, совершаемая для сообщения максимального перемещения упруго-пластической системе; Aymax – работа, совершаемая при сообщении максимального перемещение упругой системы; αT – отношение предельной нагрузки к расчётному сейсмическому весу системы (аналог коэффициента KG [14] – А.С.); p – круговая частота свободных упругих колебаний системы.

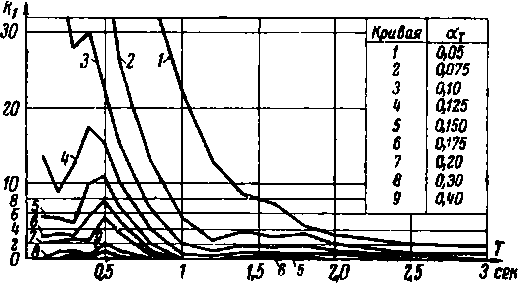
Для различных значений коэффициента k ₁ А.С. Тяном представлены графики в функции периода упругих колебаний Т и α T (рис. 2). Дополнительно выполнено их сравнение с кривыми формата К с - в i (по СНиП II-A.12-62), что позволяет оценить, насколько можно уменьшить предельную нагрузку упруго-пластической системы по отношению к сейсмической силе упругой системы (т. е. позволяет определить коэффициент редукции системы R [1] – А.С.).

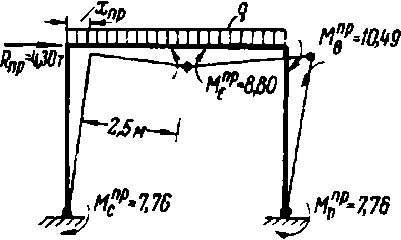
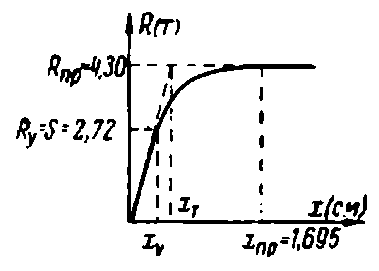
Отмечается, что если допустить степень развития пластических деформаций k ₁ = 2, то α _T меньше значения, полученного по упругому спектру реакции, в среднем в 2 раза. Результатами расчётов по способу Тяна являются картина распределения пластических шарниров, эпюры M и Q , строится кривая равновесных состояний (рис. 3).

Для рассматриваемой рамы расчётное значение сейсмической силы по нормам получилось равным 2,72 т; максимальное упругое перемещение x y – 0,42 см. После расчёта с применением упругого спектра реакции, А.С. Тяном получена фактическая сейсмическая сила ≈ 9,5 т. Из расчёта предельного состояния по Б.Г. Нилу для R _пр получено значение 4,3 т, α _T ≈ 0,2. При этом в начале реализации крайнего пластического шарнира определено максимальное горизонтальное перемещение x пр ≈ 1,7 см. Оценивая полученные результаты с применением положений работы [1], можно сделать следующие выводы. Коэффициент редукции сейсмических сил R для системы равен 3,49. Произведение коэффициентов редукции R_R·R_S равно 1,58, и тогда коэффициент редукции пластичности перемещений получается равным R _μ = 2,21. Применяя для рассматриваемой системы классическую концепцию эквивалентных энергий Ньюмарка – Холла (1982), получаем коэффициент пластичности ц R равным = 2,95, что при использовании эквивалентной билинейной аппроксимации кривой несущей способности (с горизонтальной полочкой) характерно значению x T = 0,57 см (а не ≈ 0,412, как указано в [16]). В соответствие с трактовкой 1, рассмотренной в работе [1], коэффициент допускаемых повреждений K 1 получается равным 0,29; из трактовки 2 следует, что K 1 равен 0,34.

• 2.3.    Методика оценки степени сейсмостойкости (прочности) конструкций Г.А. Шапиро – В.Ф. Захарова (ЦНИИЭП жилища, 1968) [17]

Методика основывается на применении зависимости «суммарная инерционная сила – амплитуда колебания верха конструкции» формата Q–A макс , полученной при натурных вибрационных экспе-

а)

б)

а)

Рис. 3. Графическая визуализация результатов расчётов рамы из упругопластического материала способом Тяна: а – схема разрушения рамы с величинами предельных моментов в зонах пластичности;

б – диаграмма деформирования рамы на однократное загружение

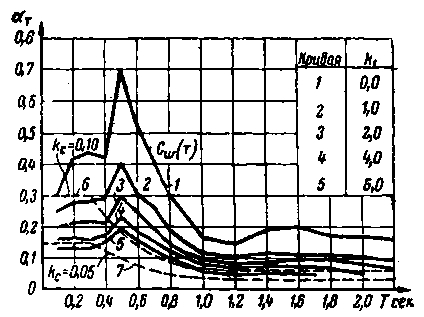
Рис. 2. Графическая визуализация зависимости от величины периода собственных колебаний Т : а – степени развития пластических деформаций k 1 , б – отношения предельной нагрузки к расчётному сейсмическому весу системы α T .

На рис. 2, б изображены следующие кривые: кривая 1 – спектр ускорений упругих систем, соответствующий 8-балльному землетрясению; кривые 2–5 – кривые α T ( Т ) при различных значениях степени развития пластических деформаций k 1 ; кривые 6–7 – спектральные кривые K с ·β i по СНиП II-А.12–62; кривая C w ( T ) – спектральная кривая, характеризующая предельное усилие упругой системы при коэффициенте рассеяния энергии у = 0,1

б)

риментах. Рассмотрены результаты испытаний ряда кирпичных, крупноблочных, каркасных, крупнопанельных и монолитных зданий. Выполнена оценка разрушения рассматриваемых систем после прохождения предельной инерционной нагрузки. Представлены кривые формата Q–А _макс/ H и φ– А _макс (где H соответствует высоте здания, φ –частоте собственных колебаний). В качестве критерия оценки сейсмостойкости принят так называемый «коэффициент запаса прочности» здания (обозначим его K _Ш-З):

кШ-З = QulL, (6) Qн где Qult – максимальная инерционная сила, определённая при эксперименте; Qн – расчётное значение сейсмической силы, вычисленное по нормам проектирования. Для применения в первом приближении рекомендуются значения KШ-З, равные 1,5; 1,8 и 2,0 для площадки с 7, 8 и 9-балльной сейсмичностью. В исследовании [17] введено понятие развитого и неразвитого резонанса для установления расчётных (проектных) значений сейсмиче- ских сил. Предложено к величине инерционной силы, полученной при развитом резонансе вводить понижающий коэффициент, учитывающий эффективность пространственной работы конструкций (обозначим его Ksp). Равен он отношению расчётной силы (здесь имеется в виду реакция VD [1] – А.С.) к значению Qult (здесь сила приводится уже с учётом её деления на KШ-З). Согласно методике Шапиро-Захарова, если величина Qult больше VD, то все последующие системы того же типа, что и испытываемая конструкция, рассчитываются на сейсмическую нагрузку по нормам, умноженную на коэффициент Ksp (для каркасных систем рекомендуется значение 0,6). Если полученная величина Qult меньше рассчитанной по нормам, то усилению подлежат слабые места конструкции (расчётные участки зон пластичности – А.С.). В качестве частного примера рассмотрены результаты испытаний крупномасштабной модели (¼ нат. вел.) 10-этажного панельного здания. Тотальное разрушение модели соответствовало реакции в уровне основания, равной 60 % от предельного значения при относительном горизонтальном перемещении верха модели 2,1 %. Идея методики Шапиро-Захарова в том, чтобы направить мысль инженера на модификацию деталей конструкции и уточнение расчётов слабых мест путём увеличения местных коэффициентов запаса (наподобие коэффициентов, предложенных В.А. Ржевским, и внедрённых в нормы проектирования в сейсмических районах Узбекистана КМК-2.01.03–96 – А.С.) в противовес общепринятому принципу о применении необоснованных коэффициентов увеличения расчётных нагрузок на всё здание в целом (позднее этот подход подтверждался результатами других исследований, например, [14, 18–21] – А.С.).

• 2.4.    Методика оценки предельных состояний многоэтажных каркасных зданий при сейсмических воздействиях

• 2.5.    Рекомендации по расчёту железобетонных рам на горизонтальные нагрузки А.А. Оганяна – М.Я. Фрайнта (ЦНИИЭП жилища, 1975) [23]

Л.Ш. Килимника (ЦНИИСК им. В.А. Кучеренко, 1975)

Объекты исследования – м н огоэ т аж н ы е кар кас ные з дан ия. Основ ная ра с чё тна я пре д пос ыл ка ме тоди ки г л а с и т, что ра с п ре де л е н ие с д в и га ющ их усилий по высоте соор уж ен ия в у пр у гой ста д и и и в п ред ел ь н ом с ос тоян и и по д обны (т. е. форма распределения сейсмических сил не ме няе тся на про тя жен ии рас чёт но й о цен к и п ри ра с с м отр ен но й с ово к у п н ост и нагр у з о к ; как в м е то де Фр им ана [13] – А.С.). Поря док ре а лиз а ц ии м е тоди ки Килимника сл е д у ющ ий . Сна ча л а произв одит с я ра с чё т ра м ы в соответствии с тре бо в а н ия м и норм ; оце ни в а ются сейсмические нагрузки S и сд в и га ющи е усили я Q в уров не пе рекрыт ий ( кром е ни жне го) и их рас пре де л е н ие по в ысоте с оор у ж е н ия. Потом н ижни й этаж рамы преобразуетс я в од ном ас с ов ый нели не йн ый ос ц илл я тор с пр ив едё н ным и па ра м е тра м и ж ёс ткости и з а т у ха н ия д л я оце нк и з на че н ия Q max о т д ейст в и я се й см и ч ес к их с ил, бл и з к их к р еа льн ы м ( сч ит ается , ч т о ма т ери а л с ист емы п од ч иня ется б и л и н е йн ой зав и с и мо с т и ) . П р и э т о м р е к о мендуе т ся и с п о льзо ва т ь спект р ы р еа кции , к от о р ы е у чит ы в ал и б ы се йсмо т е к т они ч ес к ие о со б енн о с ти р ег и он а и г ид р о г ео лог и чески е ус ловия пло щ адки с т р о ит е л ьства. Далее с учётом Q _max оце н ивае т с я р ас п р едел е ни е п о вы сот е с и ст ем ы п ред е льн ых сдв и г ающи х усилий Q _пр. Принимается, ч т о сд виг ающ ая сила в упруго-пластической системе ( Q _пр ) о р и е н ти р о во чн о составляет 60 % о т зн ач ения , п о л уч е нн о г о и з линейного анализа ( Q ). Н а с л едую щ ем э тапе мо д ель р азб ивае т ся н а п р о с т ы е о дно э т аж н ы е р амы , со ед и н я емые п о вы со те п р о с т ы м и ш арни р ами . Рассматрива ет с я п р и нцип с во б о ды вы б о р а во змо ж н ых перемещений по Н.В. Ахвледиани ( 1 9 6 3 ) [ 2 2 ] . В ел и ч ин ы п р е д е льн ых уп руг их у г ло в п о во р о т а к о лонн и р и г е лей о п р е д е ляю тся и з в ыр аже н ия :

Y y = ^Mm ,                                   (7)

6i где Mm – изгибающий момент в элементе рамы, соответствующий образованию пластического шарнира. Выражения для определения предельных упругих сдвигов этажей Δy/h и предельных упругих сдвигающих усилий Qy представлены в табулированном виде, и принимаются в зависимости от расчётной схемы одноэтажной рамы. Предельные углы поворота Ymax определяются способностью колонн и ригелей к пластическому деформированию и назначаются по результатам анализа и обобщения экспериментальных и расчётнотеоретических исследований. На этом этапе предполагается, что установлена связь между деформационными параметрами рамы и составляющих её элементов, и определены параметры интегральной зависимости типа «восстанавливающая сила – перемещение» для отдельных этажей. По ней определяются предельные значения коэффициентов податливости для колонн и ригелей. Рассматриваются два механизма пластического деформирования. Наиболее благоприятная схема деформирования соответствует балочному механизму, при котором образование пластических шарниров допускается только в элементах ригелей. В качестве примера рассмотрена оценка сейсмостойкости 10этажной рамы стального рамного каркаса.

Объекты исследования – двумерные многоэтажные однопролётные рамы из сборных железобетонных элементов с гибкостью не более 7. Сейсмическая реакция системы оценивается с применением графической зависимости «суммарная нагрузка – характерное смещение». Нелинейность работы рядового несущего элемента сведена к нелинейности работы его опорных частей. При проведении нелинейного расчёта принималось, что все сечения элементов (кроме примыкающих к узлам) работают упруго, а работа опорных сечений учитывается через нелинейную обобщённую диаграмму состояния «момент – угол искажения» M -φ _u (рис. 4). Разрушение элемента характеризуется углом искажения φ _m .

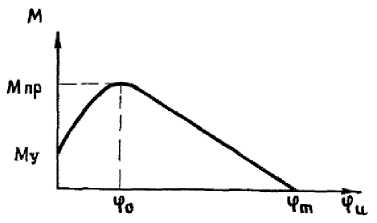
Рис. 4. Графическая визуализация диаграммы состояния «момент – угол искажения в опорном сечении» ( М– φ u ) по Оганяну–Фрайнту (1975) [23]: M пр – изгибающий момент при максимальной нагрузке; M y – изгибающий момент, до которого работу элемента можно считать упругой; φ 0 – угол искажения, соответствующий значению M пр

Максимальная допускаемая нагрузка опреде- ляется методом предельного равновесия по А.А. Гвоздеву (1936). При этом применяется модальная схема распределения сейсмических сил по высоте системы [13]. Влияние гравитационных нагрузок учитывается только при определении жесткостных характеристик элементов системы и для оценки по прочностному критерию. Основную часть исследования занимает вопрос определения параметров диаграммы M–φu, учитывающей податливость сопряжения ригелей и стоек рамы. От- мечается, что параметры диаграммы в основном зависят от степени обжатия n и степени насыщения сечения продольной арматурой ω′. Первая определяется из выражения (8), вторая – из (9):

n =

N

^R пр ^{F ,}

to' =

F a R a

^{F R} пр ^,

где N – продольное усилие в элементе; Rпр – призменная прочность; F – площадь сечения элемента; Fa – площадь сечения растянутой арматуры; Ra – расчётное сопротивление арматурной стали. При этом характеристика жёсткости расчётного участка элемента, в котором образуется зона пла- стичности, определяется из следующего выражения:

С пр = ‘ т

6 a y

1 -a y ,

где iT – погонная жёсткость элемента при образовании трещин, определяемая из выражения (11); a y - коэффициент, характеризующий изменение жёсткости при достижении предельного момента, определяемый из выражения (12).

0 , 85 E _б J _б

‘^T = —i— •

V

+0 , 043-+0 , 33 n h

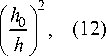
a_y =1 0 , 043+1 , 64

E a Ц

E_б 100

где E б J б – жёсткость элемента при упругой работе; l – длина элемента; E а и E б – модули упругости арматуры и бетона соответственно; μ – процент армирования сечения; l ' – расстояние от рассматриваемого сечения до нулевой точки на эпюре моментов; h – высота сечения; h 0 – рабочая высота сечения. Поясняется, что от степени обжатия также зависит и относительная величина α φ (соответствует коэффициенту пластичности – А.С.):

аФ

Ф m

Ф 0

В качестве одного из результатов статического расчёта принимается зависимость между смещением верха системы и нагрузкой (при её монотонном возрастании до заданной величины). Отмечается зависимость сейсмостойкости системы от вида её прогнозируемого разрушения (пласти- ческого, хрупкого и соответствующего промежуточной величине деформаций). При этом характер разрушения рам и способность их к деформированию предлагается оценивать после достижения предельной нагрузки. При рассмотрении частного примера двухэтажной рамы с процентом армирования ригелей и стоек рамы (≈0,6 %) значение коэффициента пластичности получается равным 3,0 (а коэффициент редукции RR [1] равным 1,25 – А.С.). В заключительной части работы отмечается, что в любом случае не следует снижать расчётную нагрузку более, чем в 2 раза (что в постановке ЛСМ актуализированных редакций СНиП II-7–81 соответствует значению K1≥0,5 – А.С.).

Анализ предпосылок, упрощающих допущений и расчётных положений рассмотренных отечественных методик позволяет отметить следующие нюансы. Способ Тяна не учитывает согласованность степеней повреждения элементов рам, предшествующих предельным значениям сдвигающей силы в уровне основания. Энергетические критерии обеспечения сейсмостойкости ( k 2 , k 3 ) при решении частной тестовой задачи не применялись. Методика Шапиро – Захарова не раскрывает вопросы оценки податливости испытанных зданий и их способность к рассеянию энергии, оперируя только коэффициентом запаса прочности. В ней рассмотрены резервы сейсмостойкости, сконсоли-дированные в объёме площади фигуры, расположенной «под кривой» равновесных состояний. В преамбуле методики Килимника отмечается важность оценки параметров глубины и протяжённости расчётных участков зон пластичности, однако в объёме расчётных положений при оценке реакции объекта исследования они не фигурируют. В методике Огаяна – Фрайнта не приводятся положения по оценке длины расчётного участка зоны пластичности и особенности специального конструирования приузловых участков.

Представляется целесообразным учесть все обозначенные нюансы, уточнить, дополнить и обобщить их в составе единой расчётной техники, доступной для применения рядовым инженером. При этом автор предлагает основные принципы и основу алгоритма построения кривой несущей способности (кривой равновесных состояний) для целей оценки реакции строительных конструкций при расчётных землетрясениях объединить общим понятием концепции нелинейного статического анализа.

• 3.    Структура предлагаемой автором методики

• 3 .1. Формула и основные расчётные положения методики

Методика определяет способ назначения армирования для объектов исследования с формированием логических связей между расчётными и конструктивными параметрами зон пластичности, образующихся в элементах их несущих конструкций при действии сейсмических сил, и устанавли- вает порядок учёта этих зависимостей для реализации благоприятного механизма пластического деформирования.

В качестве базиса методики приняты теоретические основы концепции нелинейного статического анализа. При этом методикой допускается использование любой из нелинейных статических процедур, рассматриваемых в разделе 2.1. Предпосылки, допущения и расчётные возможности составляющих её математических алгоритмов, обуславливают область применения изложенной методики. В частном случае, в качестве инструментария для построения кривой несущей способности применяются утилиты, специально сгенерированные автором с применением средств программирования системы компьютерной математики MathCAD, и алгоритм трансформации метода спектра несущей способности, реализованного в программном комплексе⁴ SAP2000. Расчётная процедура Фримана была выбрана не случайно. В ней содержится вполне обоснованный механизм учёта фактической категории технического состояния несущих конструкций через коэффициент κ (каппа), уточняющий значение параметра затухания ξ 0 для оценки коэффициентов редукции расчётного спектра ответа [9]. Она прошла практическую апробацию при оценке дефицита сейсмостойкости серии зданий различных конструктивных систем [15], в том числе после разрушительных землетрясений в Borah Peak (1983), Whittier Narrows (1987), Loma Prieta (1989) и Northridge (1994). В то время как её современные модификации, составляющие фонд методологии нелинейного статического анализа, апробированы на несложных, преимущественно каркасных системах, без учёта конструктивных особенностей зон пластичности, используются в основном для исследований. С их применением задача теряет прикладной характер, поскольку они напрямую не реализованы ни в одном специализированном инженерном программном комплексе.

Основной особенностью методики является структурирование процесса расчётного анализа сейсмостойкости объектов исследования путём его деления на последовательные этапы (стадии). Из обзора существующего уровня техники многоуровневого расчёта, выполненного автором в работе [7], можно сделать вывод, что «стадийность» процесса сейсмостойкого проектирования определена, как правило, двумя базовыми расчётными ситуациями, учитывающими интенсивность и повторяемость воздействий, возможность реализации их афтершоков, расчётные модели и методы учёта пластических деформаций конструкций, а также рассматриваемые предельные состояния и критерии оценки их наступления. При этом проявилось всё многообразие комбинаций этих составляющих, вследствие чего представление о многостадийном расчёте получило частную идентификацию. Анализируя опыт реализации расчётов на МРЗ в постановке СП 14.13330, многие практикующие специалисты и учёные в области сейсмостойкого строительства и теории сейсмостойкости сооружений на разных интеллектуальных площадках отмечают, что использование пары ПЗ-МРЗ внесло при актуализации СНиП II-7–81* много путаницы. Характерные проблемы, с которыми столкнулись проектировщики при реализации положений свода правил, пояснены, например, в работах [2, 3, 24, 25]. Специалисты отмечают, что лучше было бы ввести для целей учёта связки ПЗ-МРЗ специальный коэффициент и согласовать его с уровнем ответственности системы (так сделано, например, в части 1 Индийских норм проектирования сейсмостойких конструкций IS 1893:2002, см. [26, с. 15] – А.С.). Рассмотренные в работе [7] методики многоуровневого проектирования имеют свои преимущества и допущения. Можно заметить, что в некоторых из них:

• –    расчёт с применением спектрального метода и расчёт на упруго-пластических моделях являются двумя несвязными, и даже альтернативными оценками сейсмостойкости;

• –    для описания нелинейных моделей в расчётной ситуации МРЗ отсутствует стратегия обеспечения пластичности системы; в частности, в них не указано, каким образом допускать возможность развития существенных неупругих деформаций несущих и ненесущих элементов и их соединений при формировании расчётных моделей;

• –    представлены только общие принципы концепции стадийного расчёта без определения условий по назначению параметров зон пластичности и критериев достаточности конструктивных мероприятий для их организации в несущих элементах;

• –    не определены критерии наступления предельного состояния в момент перед обрушением системы при действии сильного (редкого) землетрясения.

• 4.    Об одной стратегии учёта параметров зон пластичности в расчётах сейсмостойких строительных систем

  • 4.1.    Онтология отечественной практики назначения параметров зон пластичности в элементах каркасных зданий

Новизна предметной области настоящего исследования состоит в формировании стадий расчёта не только с учётом интенсивности воздействия и выбора метода расчёта, но и для разделения процесса оценки параметров армирования несущих конструкций при воздействии сейсмических сил. Действия предлагается совершать в следующей последовательности. Сначала от действия эксплуатационных нагрузок и слабого (частого) землетрясения на расчётной модели, соответствующей упругой области деформирования, с примене- нием ЛСМ (при K1 = 1,0) в редакции СНиП II-7– 81* (2000 г.) и прочностного критерия по предельному состоянию I группы, определяются параметры продольного армирования несущих элементов. В качестве частого (слабого) землетрясения для объектов исследования принимается событие с уровнем сейсмического воздействия в 2 раза меньше значения, соответствующего расчётной сейсмичности площадки, устанавливаемой по данным геофизических исследований или с применением карт ОСР. Затем, на так называемой переходной стадии, с применением опыта разрушительных землетрясений предварительно рассчитываются и назначаются расчётные и конструктивные параметры прогнозируемых зон пластичности, принимается их расположение в объеме системы. На следующем этапе, от действия сильного (редкого) события, соответствующего расчётной сейсмичности площадки строительства, на модели, учитывающей возможность развития неупругих деформаций в несущих конструкциях, анализируется достаточность насыщения зон пластичности поперечной арматурой при соблюдении соответствующих критериев необрушения системы. При этом используется наиболее подходящая нелинейная расчётная процедура, учитывающая особенности принципиальных объёмно-планировочных и технических решений конкретного объекта. Для такой оценки может потребоваться несколько расчётных итераций с корректировкой расчётных параметров зон пластичности. Предлагаемые автором уточнения позволят привести коэффициент редукции RS (учитывающий приемлемое превышение напряжений в сечениях конструкций) к адекватному значению [1], и обеспечат возможность учёта параметров зон пластичности уже на этапе расчётной оценки сейсмической реакции системы, а не только непосредственно «перед конструированием». Изложенные автором расчётные положения берут начало от инженерного анализа последствий землетрясений и концепции учёта энергии, рассеиваемой за счёт упругопластических деформаций конструкций [9]. Методика учитывает принципиальные положения базового метода расчёта СНиП II-7–81* (2000 г.); одним из прикладных результатов её применения является уточнённое значение коэффициента допускаемых повреждений K1 [27].

Методикой предусматривается ряд расчётных положений, направленных на решение проблем трёх основных направлений. Во-первых, на обеспечение достоверности оценки интенсивности сейсмических сил. Во-вторых, на обеспечение способности конструктивной системы к пластическому деформированию при их воздействии. И отдельное место уделяется вопросам формирования группы критериев наступления предельного состояния по необрушению (в формулировке ГОСТ Р 54257-2010 – абсолютное предельное со- стояние), связанных с положением точки свойств на кривой несущей способности.

При определении интенсивности сейсмических сил для обоих уровней воздействия применяются спектральные кривые, указанные в пункте 3.2.2 Еврокода-8, масштабируемые через коэффициент η (эта) за счёт применения эмпирических зависимостей (рассмотренных в работе [9]) с оценкой параметров затухания ξ (кси), в том числе по результатам натурных экспериментов (например, [28]). Тело конструктивных элементов между участков, на которых прогнозируется образование зон пластичности, моделируется линейно-упругим. После вычисления сейсмических сил для нелинейных загружений, изгибная жёсткость таких элементов корректируется за счёт введения понижающих коэффициентов, интегрально учитывающих наличие трещин и неупругие свойства железобетона. Например, в первом приближении можно принять для несущих ригелей 0,5, для колонн – 0,7, для стен – 0,8 (для диафрагм – 0,4 к сдвиговой жёсткости).

Результаты применения методики обуславливаются параметрами зон пластичности, представляемыми в виде зависимостей формата «изгибающий момент – кривизна» ( M– φ) и «изгибающий момент – угол поворота» ( M– θ), отличительные особенности определения которых формируют стратегию изучения предмета исследования.

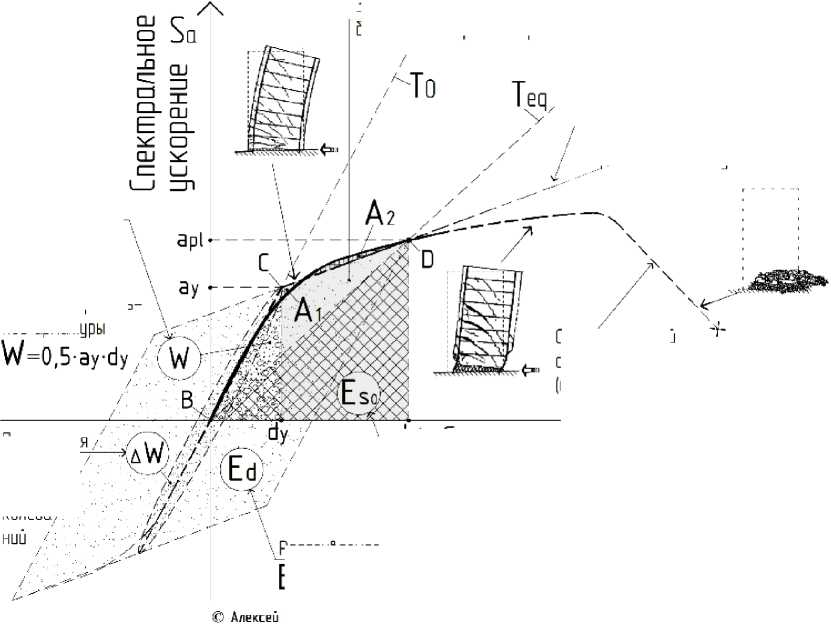
Специалистами в области сейсмостойкости сооружений установлено, что наиболее благоприятным для каркасных зданий является механизм пластического деформирования «сильные колонны – слабые ригели» (в зарубежной практике он определяется, как beam sway mechanism или «strong column – weak beam» mechanism). В случае его реализации при сильном (редком) землетрясении сейсмическую реакцию системы допускается считать прогнозируемой [29–32]. Чтобы при этом обеспечить зданию необрушаемость, зоны пластичности в несущих элементах должны обладать способностью принимать и возвращать большие количества энергии на единицу объёма [9] (рис. 5). Для этого участки элементов, на которые приходятся зоны пластичности, вне зависимости от этажности и функционального назначения зданий необходимо специально организовывать (располагать и конструировать, обеспечивая при этом их ремонтопригодность). Если зоны пластичности не будут дóлжным образом устроены, то конструкция (или её часть) может получить серьёзные повреждения или разрушиться.

Знергия. рассеиваемая зо счёт работы □Вжатого 5втпна и поперечной арматуры Ь зонах пластичности

Eso~O,5-api-dpi

Викшоробич CdcHUH, 2017 I Kmmn?lnniE мпфичрских гдгериппо! йм рпзр?и.б44.1Я пбпзрп I и баз рамщения Йтигмой пс=ма хпря.|йп

Рис. 5. Схема распределения потенциальной энергии, затрачиваемой для реализации механизма пластического деформирования при действии сейсмических сил

Билинейная аппроксимация

/ спектра несущей способности при обеспечении условия Ai=A2

Полная энергия упругих колеВа-ний, характеризуемая работой бетона и проВаль ной

Спектр несущей способности системы [Capacity Spectrum)

Потерянна; знергия . упругих ' колебат' '

\ dP[ Спектральное перемещение $z

\ Потенциольная энергия, требуемая Зля реализации оцениваемого механизма йеформиробания системы

Рассеиваемая знергия землетрясения

Ed~4-(aydpldyapl)

Отечественной практикой проектирования железобетонных каркасных зданий массового строительства в сейсмических районах допускается параметры поперечного армирования зон пластичности в ригелях и колоннах вне зависимости от их длины определять по прочностному критерию только из условия восприятия наклонным сечением поперечной силы Q. Их жёсткие узлы рекомендуется усиливать сварными сетками, спиралью или замкнутыми хомутами, выполняемыми в соответствии с положениями правил проектирования железобетонных конструкций. Интенсивность сил Q в элементах объектов исследования по нормам определяется из расчётов на сочетания, учитывающие эксплуатационные воздействия и сейсмические нагрузки, уменьшенные в (K1)–1 раз. Определенная по Q замкнутая поперечная арматура в ригелях и колонах, начиная от границ жёсткого узла, перманентно устанавливается с шагом не реже 100 мм на при-узловом участке длиной не более ¼ высоты этажа или пролёта ригеля. В проекте СТО РУДН «Строительство в сейсмических районах. Нормы проектирования сооружений» (2011; руководитель темы Курзанов А.М.) в дополнение к этому предложено за длину участков усиленного поперечного армирования колонн принимать наибольшую из двух величин 1,5b или 0,17l (где b – наибольший размер поперечного сечения элемента, l – высота колонны в свету).

Рассмотрим разницу в оценках поперечных сил на примере расчетов 15-этажного железобетонного каркасного здания [14, 33]. В табл. 1 представлены значения поперечных сил и предельных значений прочности наклонных сечений в его характерных ригелях. Принималось, что проект объекта исследования разработан с применением только ЛСМ (с K 1 = 0,25) по СНиП II-7–81* (2000 г.), а на площадке строительства прогнозируется сильное (редкое) землетрясение, характеризующееся ускорением в уровне основания 0,1 g при повторяемости воздействия один раз в 500 лет.

В качестве критерия необрушения принято положение точки упруго-пластических свойств вблизи левой границы участка кривой, характеризующей допустимые повреждения несущих конструкций ( IO R ), при достижении относительного горизонтального перекоса этажа постоянного значения 0,5 %. Поверочная оценка сейсмостойкости выполнялась с применением метода Фримана в комплексе SAP2000. Из табл. 1 следует, что в коротких ригелях рассматриваемого здания значения поперечной силы, вычисленные с применением ЛСМ, недооцениваются на 50 %, а продольное усилие – на 70 %. При коэффициенте условий работы φ b 2 равном 1,0 в редакции СП 63.13330.2012

Таблица 1

Сравнительная оценка расчётных усилий и предельных значений прочности наклонных сечений несущих ригелей 15-этажного каркасного здания [14, 33]

№ п/п	Марка 2 элем. (этаж)	Расчётные3 усилия в элементах, кН					Предельные5 значения прочности наклонных сечений элементов, кН								Примеч.
		по ЛСМ4		по НСМ		Откл. Q от V 2 , %	Q по СП63.13330.2012			Vn 7 по ACI 318				Откл.9 Q от Vn , %
		Q	N	V 2	P		без учёта N		общ. с уч. N	без учёта N		общ. с уч. N	общ.8 с уч. N
							Qb	6 Qsw		Vc	Vs
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	Рм4 (типов.)	186	+47	402	+157	54	365	124	446	189	221	411	535	17	сейсм. по Х
		353	-25	383	-128	8			493	208		429	554	11
2	Рм2 (1 надз.)	118	+108	53	+147	55			397	190	225	416	543	27	сейсм. по Y
		147	-36	136	-18	7			503	186		412	539	7