Методика формирования признака состояния воздушных объектов по совокупности радиолокационных дальностных портретов при широкополосном зондировании

В [1, 2] говорится, что наряду с традиционными (обнаружение и разрешение целей, измерение координат и параметров их движения) в число основных задач радиолокационного наблюдения выдвинулось распознавание классов, типов и функционального состояния воздушных объектов (ВО).

В [3-5] достаточно широко представлены методы и алгоритмы распознавания классов и типов ВО. В [6] предложен метод распознавания маневра ВО, но не рассматривается процесс их разрушения. В [7, 8] автор предлагает способ определения момента фрагментации объекта, но рассматривает только процесс кинетического взаимодействия космических аппаратов с астероидами и другим объектами. Однако оценка функционального состояния аэродинамических ВО радиолокационными методами остается нерешенной, поэтому актуальность рассматриваемой темы достаточно очевидна.

Под функциональным состоянием воздушного объекта понимается его положение в пространстве по отношению к радиолокационной станции (РЛС) (прямолинейное движение или совершение какого-либо маневра) и геометрическое расположение его составных частей по отношению друг к другу (разрушение или разделение), которое может быть определено по отраженному сигналу.

Как известно, отраженный от цели сигнал при высоком разрешении имеет достаточно сложную временную структуру, которая определяется геометрическими и электродинамическими особенностями. Такой сигнал после согласованной обработки и амплитудного детектирования дает радиолокационный дальностный портрет (РЛДП). Реализация РЛДП зависит не только от геометрической формы воздушного объекта (ВО), но и от ориентации его элементов – 326 – относительно линии визирования РЛС. Поэтому нами выдвинута гипотеза о том, что РЛДП ВО как при маневре, так и при разрушении претерпевает существенные изменения, однако при маневре они могут носить регулярный характер, а при разрушении – хаотичный. Анализ динамики РЛДП позволит классифицировать ВО по состоянию: прямолинейное движение/маневр/ разрушение (рис. 1).

Для проверки выдвинутой гипотезы были рассмотрены три возможных состояния ВО: прямолинейное движение, маневр и разрушение.

Для анализа был выбран метод математического моделирования, основанный на преобразовании 3D-моделей ВО в дифференциальную эффективную поверхность рассеяния (ЭПР), свертки ее с зондирующим сигналом и последующей согласованной обработки с вычислением модуля выходного сигнала (рис. 2), который подробно описан в [9].

Динамика РЛДП оценивалась по признаку в виде коэффициента корреляции (КК) между текущим и предыдущим РЛДП в соответствии с выражением

„         Z(x fc -x)(y fc -:y)

т =------------- xy  №г*)2%УгУ)2, где xk - РЛДП ВО в момент времени 11; X - среднее значение x по выборке X; yk - РЛДП ВО в момент времени 12; у - среднее значение у по выборке Y.

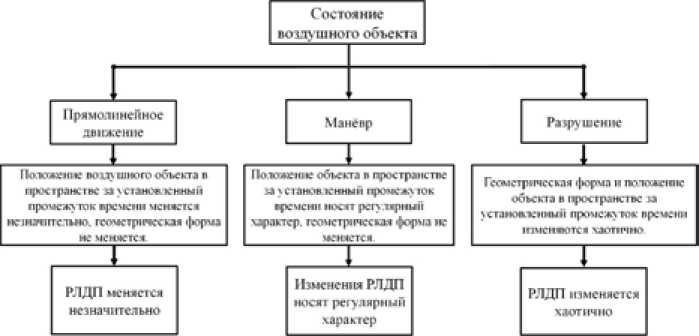
Рис. 1. Классификация состояния воздушных объектов и описание признаков на основе РЛДП

Fig. 1. Classification of the condition of the objects and a description of the characteristics based on radar long-range portraits (RLRP)

Рис. 2. Этапы математического моделирования РЛДП

Fig. 2. Stages of RLRP mathematical modeling

Для проведения эксперимента были разработаны модели процессов разрушения и маневра типового воздушного объекта.

Процесс разрушения ВО в результате кинетического воздействия либо технической неисправности является случайным, поэтому для его анализа были использованы видеоматериалы реальных событий с ВО. В качестве прототипа варианта разрушения был взят видеофайл, отдельные кадры которого представлены на рис. 3.

Время анализа ограничено одной секундой, так как за этот промежуток происходят существенные изменения геометрической формы ВО. На основе имеющихся видеоматериалов в программе 3Dmax разработаны покадровые модели ВО, соответствующие по характеру изменения геометрической формы объекту из видеофайла (рис. 4).

Формирование покадровой последовательности из 25 РЛДП проводилось описанным выше методом математического моделирования [9].

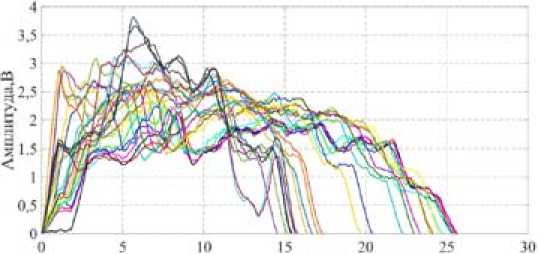
На рис. 5 и 6 представлены совокупности РЛДП разрушающегося ВО №1 при сигналах с шириной спектра (ШС) 30 и 300 МГц соответственно.

Для представленных на рис. 5, 6 совокупностей РЛДП по формуле (1) рассчитаны значения КК. Минимальное значение КК при сигнале с ШС 30 МГц составило 0,95, при сигнале с

Рис. 3. Отдельные кадры процесса разрушения ВО

Fig. 3. Individual frames of the process of destruction of aircraft object (AO)

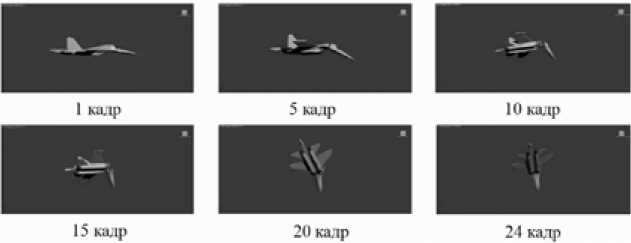
Рис. 4. 3D-модели разрушения воздушного объекта №1

Fig. 4. 3D-models of destruction of air object №1

ПрогяжтнносткРЛДЦ.ч

Рис. 5. Совокупность РЛДП разрушающегося ВО №1 при сигнале с ШС 30 МГц

Fig. 5. Set of RLRP of the collapsing air object №1 at the signal with a spectrum width of 30 MHz

Протяженность РЛДП, м

Рис. 6. Совокупность РЛДП разрушающегося ВО №1 при сигнале с ШС 300 МГц

Fig. 6. Set of RLRP of the collapsing air object №1 at the signal with a spectrum width of 300 MHz

ШС 300 МГц – 0,72. Для получения достаточной статистики было реализовано несколько вариантов разрушения четырех типов ВО с различных ракурсов. Во всех экспериментах рузульта-ты имели достаточную сходимость: среднее значение КК при сигнале с ШС 30 МГц составило не менее 0,9, а для сигнала с ШС300 МГц – не менее 0,7.

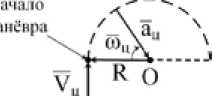
Маневр воздушного объекта – это процесс, близкий к детерминированному. Поэтому его можно представить в виде движения по окружности радиусом R (рис. 7).

В случае пилотируемого полета предельное значение длительной перегрузки не может превышать значения 10 g , что соответствует пределу физиологических возможностей человека.

При этом связь между параметрами движения и радиусом кривизны траектории R определяется выражением

Я ц = ^ Ц- = Ш^Н ,

где V ц – тангенциальная составляющая скорости объекта в точке начала маневра; ω ц – угловая скорость движения объекта по окружности; R – радиус кривизны траектории движения объекта.

Равномерное пряммкейное движение

Рис. 7. Модель выполнения процесса маневра ВО

Fig. 7. The execution model of the AO maneuver process

Таблица 1

Table 1

V ц , м/с	100	200	300	400	500	600	700	800	900	1000
R, м	102	408	918	1632	2551	3673	5000	6530	8265	10204

С учетом перегрузки n – отношения абсолютной величины линейного ускорения цели aц, вызванного негравитационными силами, к ускорению свободного падения g, имеем:

Яц П = ц д

V ?

пд=^ = o^R.                                     (4)

Таким образом, угловая скорость вращения относительно РЛС, которая приводит к изменению РЛДП, зависит от тангенциальной составляющей скорости цели и допустимых значений перегрузки. Рассчитанные радиусы кривизны траектории маневра для скоростей ВО от 100 м/с до 1000 м/с представлены в таблице 1.

Дальнейшие результаты представлены для модели маневра при скорости движения ВО в 300 м/с. Исходя из этого скорость ω будет равна 0,33 рад/с, что соответствует повороту ЛА относительно РЛС со скоростью 19º/с.

На рис. 8 и 9 показаны совокупности РЛДП маневрирующего ВО №1 при углах курса β =0-19º с шагом 1º и ширине спектра зондирующего сигнала 30 и 300 МГц соответственно.

Для представленных на рис. 8 и 9 совокупностей РЛДП по формуле (2) рассчитаны значения коэффициентов корреляции между текущим и предыдущим реализациями РЛДП. Все значения коэффициентов корреляции лежат в пределах значений 0,9-0,99.

На рис. 10 показаны графики изменения коэффициентов корреляции ВО №1 для сигналов с ШС 30 и 300 МГц для маневра и разрушения.

На рис. 10 видно, что КК РЛДП не опускается ниже уровня 0,7 при сигнале с ШС 300 МГц, а при сигнале с ШС 30 МГц – не ниже 0,95.

Отношение коэффициентов корреляции при маневре и разрушении составили 1,04 и 1,36 для 30 и 300 МГц соответственно, что свидетельствует о малой контрастности признака.

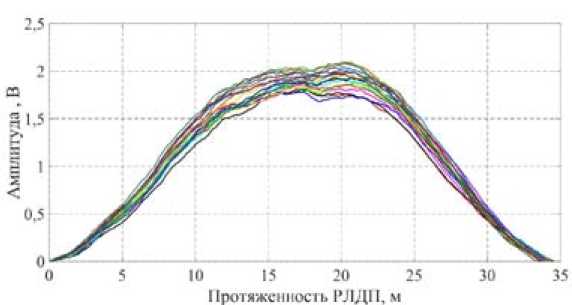
Рис. 8. Совокупность РЛДП маневрирующего ВО №1 при углах курса β =0º-19º для сигнала с ШС ширине спектра 30 МГц

Fig. 8. Set of RLDP for maneuvering AO №1 at angles of β =0º-19º for signal spectrum width spectrum width of 30 MHz

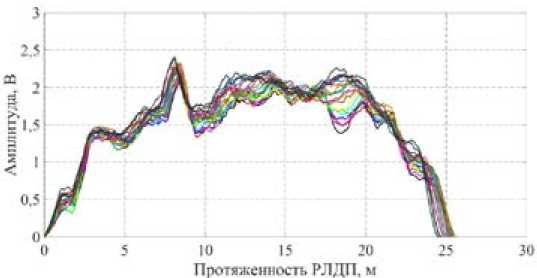
Рис. 9. Совокупность РЛДП маневрирующего ВО №1 при углах курса β =0-19º для сигнала с ШС ширине спектра 300 МГц

Fig. 9. Set of RLDP for maneuvering AO №1 at angles of β =0º-19º for signal spectrum width spectrum width of 300 MHz

Таким образом, гипотеза о существенном изменении РЛДП при маневре и разрушении подтвердилась, однако значения выбранного признака оказались невелики, поэтому для повышения контрастности выбранного признака (КК) целесообразно провести дополнительную обработку.

Для решения этой задачи была использована двухэтапная процедура вейвлет-преобразования, предложенная в [5] для формирования контрастных признаков распознавания радиолокационных целей.

На первом этапе для каждого РЛДП вычисляются вейвлет-коэффициенты W z ( a , b ) в соответствии с выражением

Ша, Ь) = ^/_” Z^yvtydt,

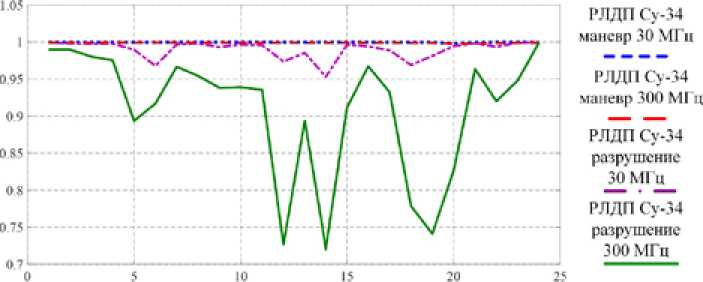
Рис. 10. График изменения КК совокупности РЛДП ВО №1 при сигнале с ШС 30 и 300 МГц для маневра и разрушения

Fig. 10. Graph of changes in the correlation coefficients of the set of RLRP of the air object №1 at a signal with a spectrum width of 30 MHz and 300 MHz for maneuvering and destruction

(?)

где Z(t) - входной РЛДП; a - параметр масштаба; b - параметр временного переноса; V базисная функция Хаара.

На втором этапе из W _z( a , b ) формируются LLE ( a , b ) – линии локальных экстремумов (ЛЛЭ) в соответствии с выражением

LLE(a,b)

Г 1,| ^^^^2 | < д^ [о, | ^dw^-^b | > д^ ^,

где Δ W – заданное пороговое значение скорости изменения функции W _z( a , b ).

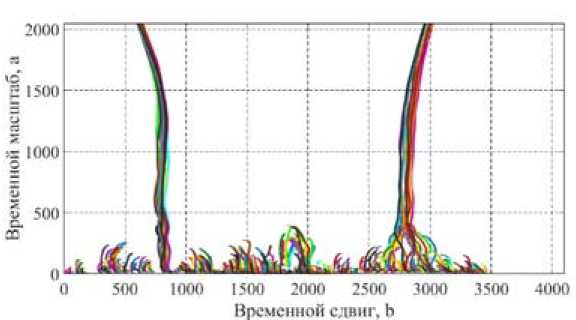
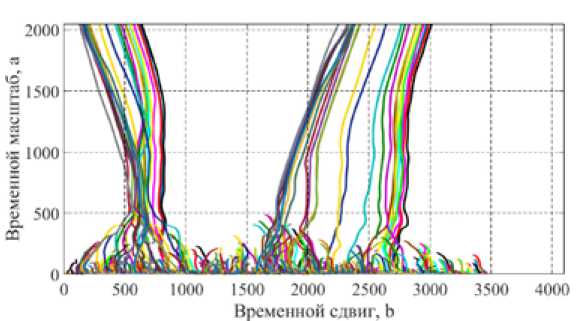
На рис. 11 представлены совокупности ЛЛЭ ВО №1 при сигнале с ШС 30 МГц для маневра и разрушения.

Характерной особенностью ЛЛЭ является их компактность и малая дисперсия при регулярном изменении РЛДП (рис. 11 а ). При разрушении цели ЛЛЭ изменяются значительно больше (рис. 11 б ).

Для оценки динамики коэффициента корреляции ЛЛЭ при маневре и разрушении был проведен статистический эксперимент, результаты которого изображены на рис. 12 и 13.

Из графиков на рис. 12, 13 видно, что среднее значение KK LLE при маневре более чем в два раза превышает значение KK _LLE при разрушении для сигналов с ШС 30 и 300 МГц, а среднеквадратичное отклонение KK LLE при маневре в 1,5 раза меньше, чем при разрушении для сигнала с ШС 30 МГц и в 3 раза меньше для сигнала с ШС 300 МГц (0,13 / 0,19; 0,06 / 0,2 соответственно).

Таким образом, предложенная на рис. 14 методика формирования признака маневра/разру-шения, основанная на вычислении линий локальных экстремумов от вейвлет-коэффициентов РЛДП, обеспечила его высокую контрастность, что может повысить качество распознавания в задаче оценки функционального состояния объектов.

а)

б)

Рис. 11. Совокупность ЛЛЭ ВО №1: а – при маневре ( β =0-19º); б – при разрушении

Fig. 11. Set of lines the local extrema (LLE): a – when maneuvering ( β =0-19º); b) with the destruction

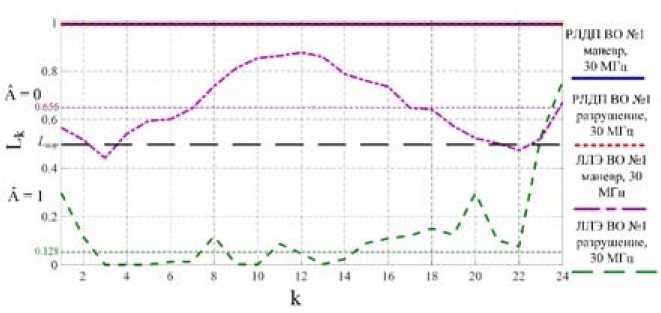
Рис. 12. График изменения КК совокупности РЛДП и ЛЛЭ для маневра и разрушения при сигнале с ШС 30 МГц

Fig. 12. Graph of changes in correlation coefficients of the set of RLRP and LLE for maneuvering and destruction at a signal with a spectrum width of 30 MHz

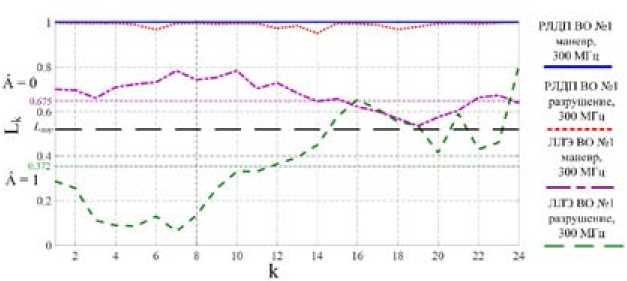
Рис. 13. График изменения КК совокупности РЛДП и ЛЛЭ ВО №1 для маневра и разрушения при сигнале с ШС 300 МГц

Fig. 13. Graph of the correlation coefficients of the set of RLRP and LLE to maneuver and destruction with a spectrum width of 30 MHz

Рис. 14. Структурная схема методики формирования признака маневра/разрушения

Fig. 14. Structural scheme of the formation method of maneuver/destruction sign