Методика формирования признаков распознавания на основе вейвлет-преобразования радиолокационных дальностных портретов

Одной из перспективных задач развития радиолокационных систем специального назначения является внедрение новых способов обработки отраженных сигналов с целью классификации объектов локации по их тактическому назначению. В основе решения этой задачи лежат методы радиолокационного распознавания, которые достаточно полно раскрыты в ряде источников [1-7]. В них указано, что наиболее эффективными считаются методы, основанные на анализе признаков в виде радиолокационных дальностных портретов (РЛДП) [5]. Большинство алгоритмов распознавания по РЛДП основаны на байесовском подходе [7]. В этом случае качество принятия решения о принадлежности объекта к заданному классу (типу) оценивается матрицей условных вероятностей распознавания. В [2, 7] утверждается, что основным средством повышения качества распознавания служит расширение спектра зондирующих сигналов и увеличение отношения сигнал-шум. Вместе с тем высокая плотность радиолокационных станций в группировке, необходимость решения задач на предельных дальностях, а также возможное радиоэлектронное противодействие ограничивают ширину спектра зондирующих сигналов и достижимое отношение сигнал-шум. В этих условиях качество радиолокационного распознавания с использованием РЛДП возможно повысить только за счет дополнительной обработки, направленной на повышение контрастности признаков.

Контрастность радиолокационных дальностных портретов

Понятие контрастности РЛДП и ее связь с показателями качества распознавания введены в работе [8]. В ней РЛДП представляется как совокупность нормально распределенных стати -стически независимых комплексных амплитуд η i , где i – количество элементов разрешения цели. Вероятность правильного распознавания цели k -го класса определяется по формуле

«кН»(Э].

2 гх где Ф(%) = -;= L е ^ at - интеграл вероятности; ркцк - среднее значение коэффициента кор-<2п о реляции pM/i между к-м текущим и l-эталонным портретом; akl/k - СКО коэффициента корреляции между k-м текущим и l-эталонным портретом при наличии цели k-го класса.

Из (1) следует, что вероятность правильного распознавания D_k зависит от интеграла ве-

Р к1/к\  .

роятности Ф I—— I. Аргумент интеграла вероятности - это отношение среднего значения ко-\ «И/к/ эффициента корреляции к СКО случайной величины akl/k при наличии цели к-го класса, который определяется выражением

P ki/k _ ^iK^-^^¹^^.

° kl/k

;

д

i _ kl =

tf2^

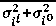
где k_kl - отношение дисперсий коэффициентов корреляции; a_t o - дисперсия собственного шума, одинаковая для всех элементов разрешения.

Величина Д_к1, характеризующая отклонение от единицы отношений дисперсий i -х элементов разрешения к -го и l -го портретов, может принимать как положительные, так и отрица- к²

тельные значения. Учитывая, что ln(1 + х) ~ х --, имеем следующие выражения:

P kl/k _ 1

" ki/k    ²

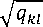
qki   Г .(-У-ч

Величина q_kl определена как контрастность между портретом, соответствующим правильному решению о наличии цели к -го класса, и другими портретами I Ф к. Следовательно, вероятность правильного распознавания D_k прямо пропорциональна величине контрастности q_kl.

Таким образом, при ограничениях на ширину спектра зондирующего сигнала и отношение сигнал-шум качество радиолокационного распознавания можно улучшить только за счет дополнительной обработки РЛДП, обеспечивающей повышение контрастности.

Методика формирования контрастных признаков распознавания

Ниже представлена методика формирования высококонтрастных признаков распознавания, основанная на линейном разложении исходного РЛДП с помощью двухпараметрических базисных функций.

В основе методики лежит ряд предположений:

• 1.    Контрастность каждого РЛДП определяется относительным объемом информации, отличающей его от других.

• 2.    Совокупность РЛДП в выбранном алфавите классов может быть представлена матрицей Z = ||z_w|| размерностью L х N , где L - количество классов в алфавите, N - протяженность (размерность) каждого РЛДП при его представлении в дискретном виде.

• 3.    Показателем контрастности может быть коэффициент парной корреляции Пирсона

• 4.    Интегральный показатель качества системы распознавания - среднее значение условной вероятности ошибки распознавания, зависит от контрастности каждой пары РЛДП:

  /^^ ^(.^ (Z f—i Z m—i P im -Z f—i P li ) ,                                  (7)

• 5.    Линейное разложение РЛДП позволяет выделить его оригинальные составляющие и использовать их для распознавания классов и типов объектов [9, 10].

у N ((7   /У/   7—А^

^Z i—1 (ДА/ ^— ^и⁾⁽ ^ тл ^— ^ тл ) J

^"Ж(^-5^^               ⁽⁶⁾

— С| С| С—L, HL|l/ где - I ф т индексы распознаваемых классов (типов) из выбранного алфавита размерностью L.

где y^ z,m (P z,m )y - матрица условных вероятностей распознавания.

Для линейного разложения сигналов применяются методы, основанные на системах ортогональных функций различного вида. К ним относятся преобразования Фурье, Уолша, – 279 – вейвлет-преобразование, преобразование Карунена-Лоэва (ПКЛ), использующие гармонические функции, функции Радемахера, Уолша, Хаара и др. Результат разложения представляется в виде одно-либо двумерного вектора коэффициентов в зависимости от вида и числа параметров базисных функций.

В контексте решаемой задачи предполагается, что особенности каждого РЛДП локализованы на некотором случайном временном интервале. Учитывая принцип неопределенности Гейзенберга, для выделения характерных особенностей каждого РЛДП методом ортогонального разложения целесообразно использовать базисные функции, локализованные как по времени, так и по частоте (масштабу) [10, 11].

Из всех вышеперечисленных преобразований этому требованию удовлетворяет вейвлет-преобразование вида

W (a , b) = ^ J " ^Z (ОД (^) dt,                              (8)

и                     и.

где Z ( t ) - РЛДП; ^_Q-b(t) — базисная вейвлет-функция.

Для дискретных значений параметров a и b результатом вейвлет-преобразования будет матрица W = |w„1 где ^ = ^/" Z(W (^ dt.

Механизм вейвлет-преобразования типового РЛДП с использованием ортогонального вейвлет-базиса Хаара приведен на рис. 1. РЛДП задан в виде вектора размерностью N. Для наглядности ось абсцисс масштабирована в единицах длины объекта (с шагом 1 см) и единицах времени (с шагом ≈ 67 пс).

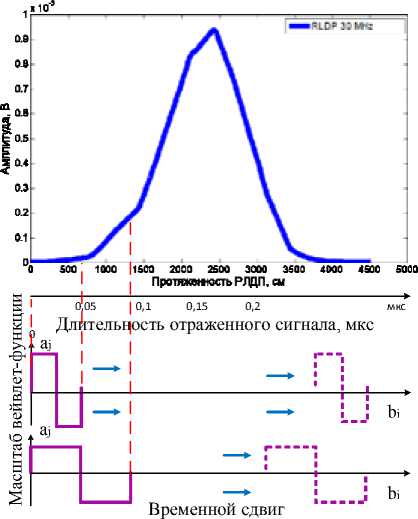
Рис. 1. Механизм вейвлет-преобразования РЛДП с использованием базиса Хаара

Матрица вейвлет-коэффициентов W_z в координатах масштаб - протяженность представлена на рис. 2 в виде поверхности. Каждый вейвлет-коэффициент W j^ характеризует среднюю скорость изменения РЛДП в пределах интервала интегрирования, которая может восприниматься как информационный элемент.

На рис. 2 видно, что поверхность, образуемая вейвлет-коэффициентами W_z , имеет поли-модальный вид. Причем по оси масштаба просматриваются устойчивые локальные экстремумы, характеризующие участок РЛДП с определенной скоростью изменения. Математическое моделирование РЛДП нескольких объектов и вычисление вейвлет-коэффициентов показали наличие экстремумов во всех случаях. Причем их положение было оригинальным для каждого из объектов.

Таким образом, первым этапом методики является разложение исходного РЛДП по ортогональному вейвлет-базису с вычислением матрицы вейвлет-коэффициентов W z .

Для выделения локальных экстремумов, характеризующих особенности РЛДП, над матрицей коэффициентов W_z проводится операция вычисления первых и вторых разностей с последующим бинарным преобразованием в соответствие с выражением

^-{ 0

Д^1лг < 0лД^2/; < 0

Д^1_лг>0УД^2_л;>0 ,

где Д^у = ^(wj_V+i ^- Wj^ • (W j,i ^{- W}j,_i-1⁾ ; kW2 j _-t = ^Wj,_i+1 + ^W j _Л -1 ^- 2W_j,_i .

На рис. 3 показаны линии локальных экстремумов (ЛЛЭ) матрицы Lw - || Iw j,_t || как результат преобразования (9) матрицы W_z . Положение и вид ЛЛЭ определяются видом РЛДП. Таким образом, второй этап методики - формирование бинарной матрицы Lw .

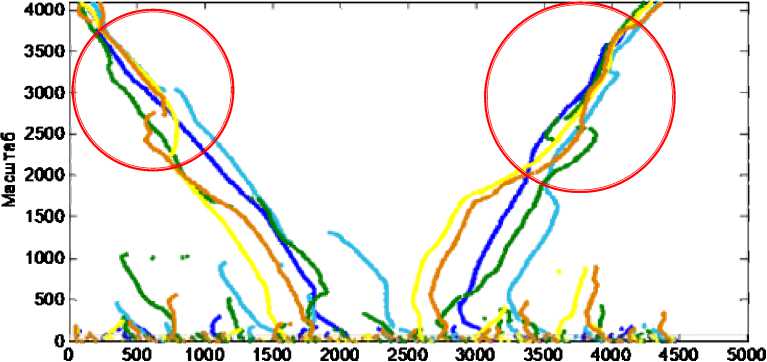
Как видно на рис. 3 и 4, количество ЛЛЭ с увеличением масштаба уменьшается. Это объясняется увеличением длительности базисной функции и интервала интегрирования в (8). В то же время положение ЛЛЭ оказывается более стабильным в пределах близких ракурсов объекта (рис. 4, области, выделенные окружностями). Следовательно, для выделения наиболее устойчивых ЛЛЭ необходимо выполнить параметрическую оптимизацию матрицы Lw путем ограничения снизу на некотором заданном уровне.

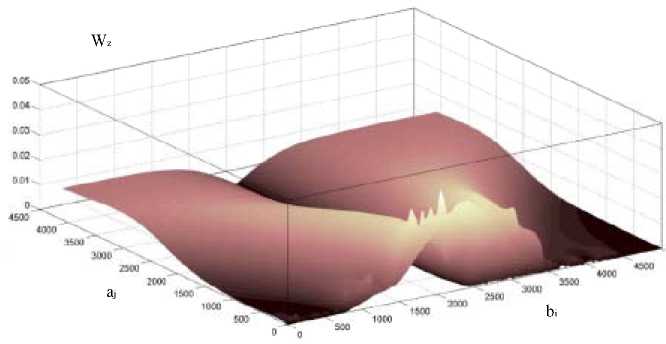
Рис. 2. Поверхность вейвлет-коэффициентов W z

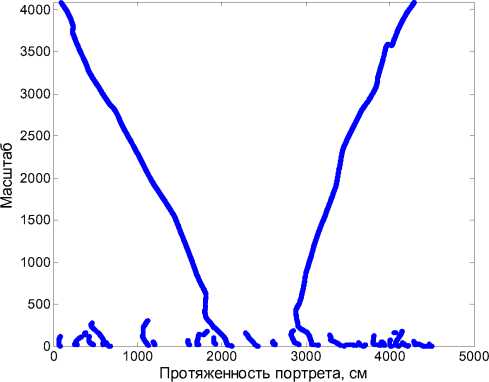
Рис. 3. Линии локальных экстремумов

Протяженность портрета, см

Рис. 4. Семейство из пяти ЛЛЭ для объекта 1 при изменении ракурса с шагом 4º

Мы выбирали уровень ограничения исходя из заданного минимального количества ЛЛЭ для каждого из объектов (РЛДП).

На практике уровень ограничения может быть определен исходя из требуемого значения коэффициента межклассовой корреляции эталонных портретов выбранного алфавита классов (типов).

Таким образом, заключительным этапом методики является операция оптимизации матрицы Lw путем выбора уровня ограничения масштаба снизу (рис. 5).

Оценка показателей качества методики формирования признаков распознавания

Эффективность предложенной методики оценивалась для алфавита типов объектов ( L = 4) в пределах одного класса, РЛДП и ЛЛЭ которых показаны на рис. 6 и 7 соответственно.

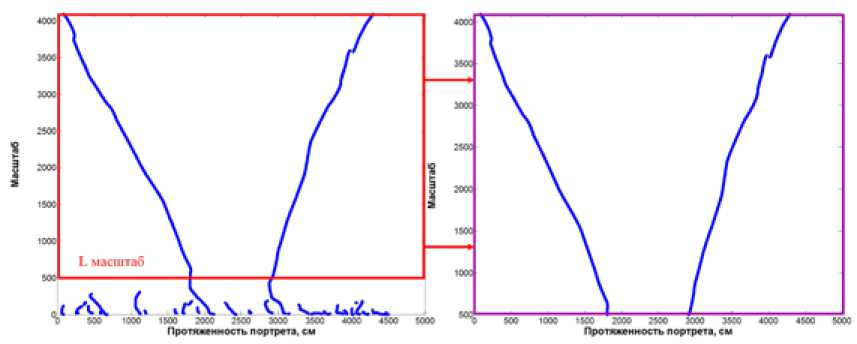
Рис. 5. Линии локальных экстремумов и уровень ограничения масштаба

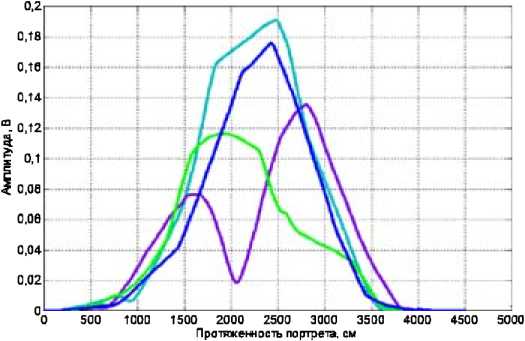
Рис. 6. Семейство РЛДП четырех типов объектов

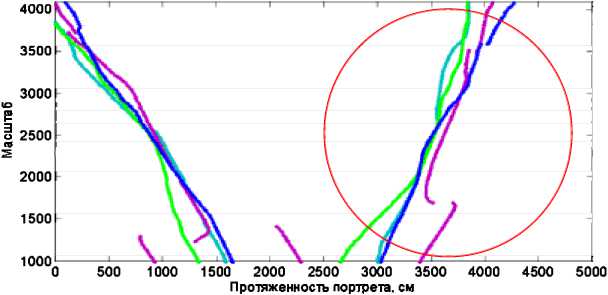
Рис. 7. Семейство ЛЛЭ для объектов различных классов

Оценка среднего значения коэффициента парной корреляции для всех пар выбранных РЛДП составила P i, _m = 0,76,, а для ЛЛЭ P i, _m = 0,03. Таким образом, контрастность признаков распознавания на основе линий локальных экстремумов вейвлет-коэффициентов по выбранному показателю более чем на порядок превышает контрастность исходных РЛДП.

Результаты математического моделирования устройства распознавания классов (типов) объектов, использующего ЛЛЭ, подтвердили выдвинутую гипотезу о монотонной зависимости показателей качества радиолокационного распознавания от контрастности эталонных признаков.

Выводы

• 1.    Линейное разложение РЛДП позволяет сформировать устойчивые, компактные, контрастные признаки распознавания.

• 2.    Контрастность признаков распознавания в виде ЛЛЭ зависит от параметров вейвлет-преобразования и выбранных уровней ограничений по оси масштаба.

• 3.    Дальнейшие исследования будут проводиться с большим алфавитом классов и пониженным отношением сигнал-шум.